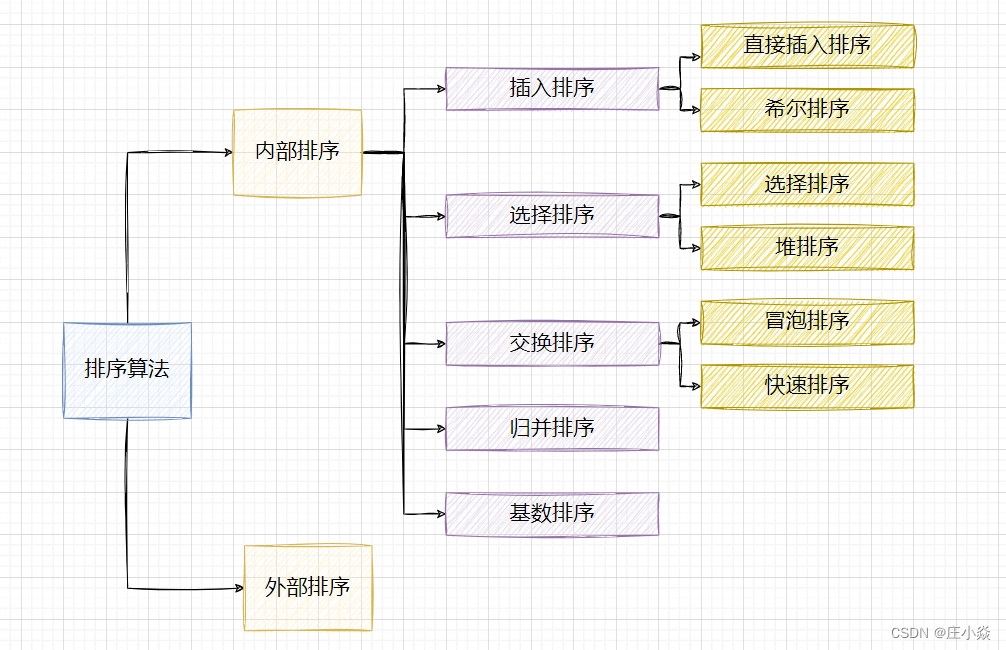
算法问题——排序算法问题
摘要
查找和排序算法是算法的入门知识,其经典思想可以用于很多算法当中。因为其实现代码较短,应用较常见。所以在面试中经常会问到排序算法及其相关的问题。但万变不离其宗,只要熟悉了思想,灵活运用也不是难事。一般在面试中最常考的是快速排序和归并排序,并且经常有面试官要求现场写出这两种排序的代码。对这两种排序的代码一定要信手拈来才行。还有插入排序、冒泡排序、堆排序、基数排序、桶排序等。面试官对于这些排序可能会要求比较各自的优劣、各种算法的思想及其使用场景。还有要会分析算法的时间和空间复杂度。通常查找和排序算法的考察是面试的开始,如果这些问题回答不好,估计面试官都没有继续面试下去的兴趣都没了。所以想开个好头就要把常见的排序算法思想及其特点要熟练掌握,有必要时要熟练写出代码。下面主要介绍经典排序算法。
一、排序算法的时间与空间复杂度分析
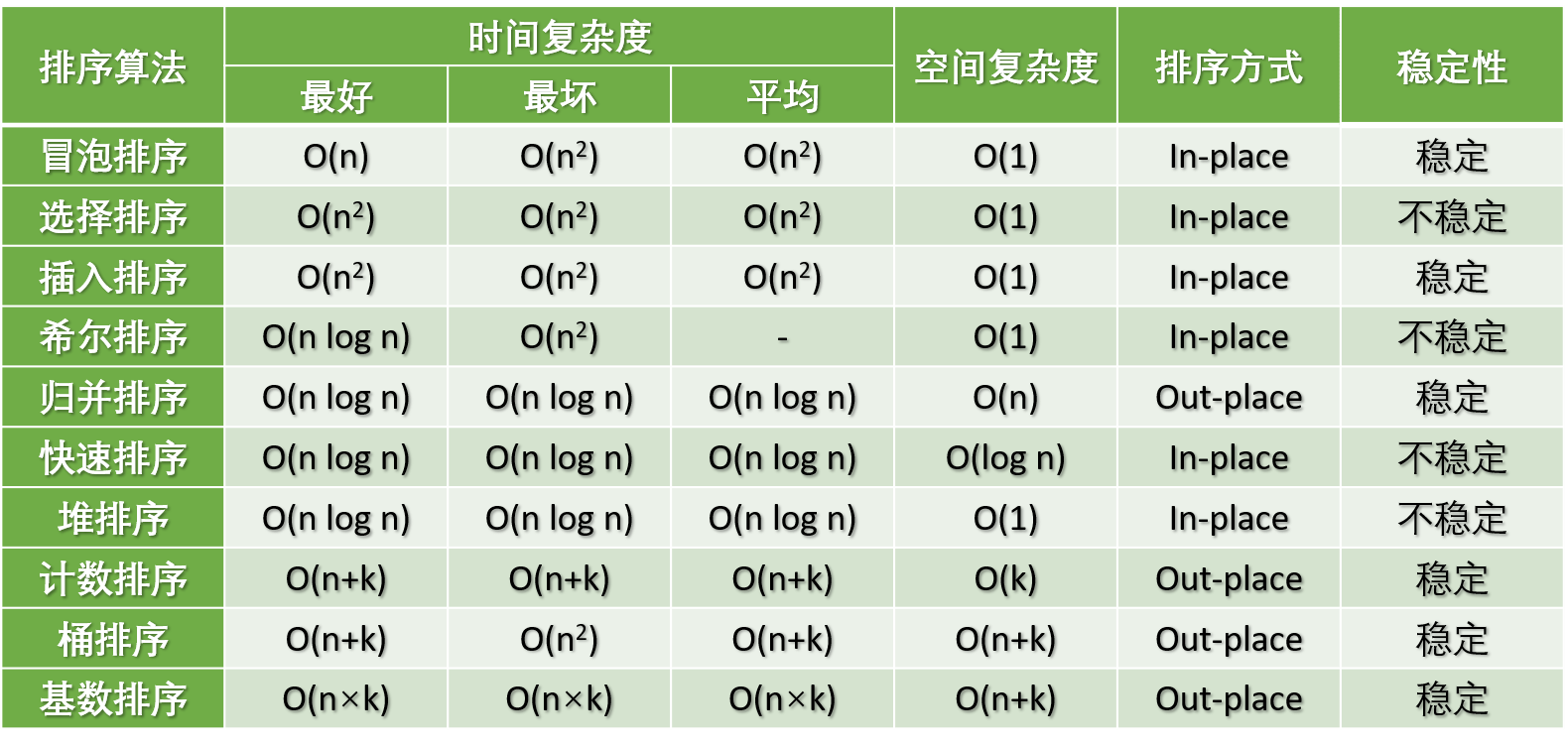
比较排序的优势是,适用于各种规模的数据,也不在乎数据的分布,都能进行排序。可以说,比较排序适用于一切需要排序的情况。
- 常见的快速排序、归并排序、堆排序、冒泡排序等属于比较排序。在排序的最终结果里,元素之间的次序依赖于它们之间的比较。每个数都必须和其他数进行比较,才能确定自己的位置。
- 在冒泡排序之类的排序中,问题规模为n,又因为需要比较n次,所以平均时间复杂度为O(n²)。在归并排序、快速排序之类的排序中,问题规模通过分治法消减为logN次,所以时间复杂度平均O(nlogn)。
非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决。算法时间复杂度O(n)。
- 计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前,应该有多少个元素来排序。针对数组arr,计算arr[i]之前有多少个元素,则唯一确定了arr[i]在排序后数组中的位置。
- 非比较排序时间复杂度底,但由于非比较排序需要占用空间来确定唯一位置。所以对数据规模和数据分布有一定的要求。
二、排序算法
2.1 冒泡排序(Bubble Sort)
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
算法描述
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
冒泡算法实现
/*** Description:冒泡排序** @param array 需要排序的数组* @author xjl* @date 2023/1/10 9:54*/
public static void bubbleSort(int[] array) {if (array == null || array.length <= 1) {return;}int length = array.length;// 外层循环控制比较轮数ifor (int i = 0; i < length; i++) {// 内层循环控制每一轮比较次数,每进行一轮排序都会找出一个较大值// (array.length - 1)防止索引越界,(array.length - 1 - i)减少比较次数for (int j = 0; j < length - 1 - i; j++) {// 前面的数大于后面的数就进行交换if (array[j] > array[j + 1]) {int temp = array[j + 1];array[j + 1] = array[j];array[j] = temp;}}}}
空间与时间复杂度
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
2.2 选择排序(Selection Sort)
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n^2)的时间复杂度,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序能也是平时排序一般人想到的最多的排序方法了吧。
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
初始状态:无序区为R[1…n],有序区为空;
第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
n-1趟结束,数组有序化了。
选择排序算法实现
/*** Description: 选择排序** @param array* @return void* @author xjl* @date 2023/1/11 23:31*/
public static void selectionSort(int[] array) {if (array == null || array.length <= 1) {return;}int length = array.length;for (int i = 0; i < length - 1; i++) {// 保存最小数的索引int minIndex = i;for (int j = i + 1; j < length; j++) {// 找到最小的数if (array[j] < array[minIndex]) {minIndex = j;}}// 交换元素位置if (i != minIndex) {swap(array, minIndex, i);}}}/*** Description: 交换元素位置** @param array* @param a* @param b* @return void* @author xjl* @date 2019/7/11 17:57*/
private static void swap(int[] array, int a, int b) {int temp = array[a];array[a] = array[b];array[b] = temp;
}
空间与时间复杂度
- 时间复杂度:O(n^2)
- 空间复杂度:O(1)
2.3 插入排序(Insertion Sort)
2.4 希尔排序(Shell Sort)
2.5 归并排序(Merge Sort)
2.6 快速排序(Quick Sort)
2.7 堆排序(Heap Sort)
2.8 计数排序(Counting Sort)
2.9 桶排序(Bucket Sort)
2.10 基数排序(Radix Sort)
博文参考
史上最全经典排序算法总结(Java实现)_ThinkWon的博客-CSDN博客
相关文章:

算法问题——排序算法问题
摘要 查找和排序算法是算法的入门知识,其经典思想可以用于很多算法当中。因为其实现代码较短,应用较常见。所以在面试中经常会问到排序算法及其相关的问题。但万变不离其宗,只要熟悉了思想,灵活运用也不是难事。一般在面试中最常…...

ArcGIS网络分析之构建网络分析数据集(一)
说明: 1. 本文主要用于演示网络分析服务的搭建过程。所以在此不会深入讨论网络分析服务的每一个细节,本文的目的就是让初学者学会使用网络分析服务进行基本的分析(主要针对后续的WEB开发):路径分析,最近设施点分析,以及服务区分析。 2.关于OD成本矩阵分析,多路径配送,…...

微电影的行业痛点有哪些?
微电影全称微型电影,又称微影。是指能够通过互联网新媒体平台传播(几分钟到60分钟不等)的影片,适合在移动状态、短时休闲状态下观看,具有完整故事情节的“微(超短)时”(几分钟-60分钟)放映、“微(超短)周期制作(7-15天…...
spark3.0源码分析-driver-executor心跳机制
前言 driver和executor心跳机制分为两种机制: 1、executor发送心跳机制 2、driver接受心跳机制 至于为何要分为两种,原因是在分布式场景中,服务的稳定性是无法保障的,例如executor宕机后无法发送心跳,故driver端需要…...
数据分析就要选择这款免费报表工具
对于一家企业来说,在日常运营的过程中本身就会产出很多的数据,那么这些数据本身就应该形成报表。可是如果只是选择手工的一种操作,确实需要浪费大量的人力物力。伴随着科技进入到快速发展的阶段,市面上更是出现了很多报表工具可以…...
node学习-3:服务器渲染和客户端渲染
1. 概念 一.服务端渲染,后端嵌套模板,后端渲染模板,SSR(后端把页面组装好) 做好静态页面,动态效果 把前端代码提供给后端,后端则把静态html以及里面的假数据给删除掉 通过模板进行动态生成h…...

LeetCode刷题笔记和周赛题解总目录
之前一段时间一直在刷LeetCode,在上面积累了很多笔记,这些笔记是做题过程中的一些重要积累和心得,现在将它们汇总和总结至此,此博客将不断更新。 刷题笔记(提供md和pdf两种格式可供下载,不断更新) LeetCode刷题笔记 …...

用类比方式学习编程中函数递归(个人理解仅供参考)(内含汉诺塔问题的求解)
目录 1.前言 2.递归的数学模型 3.相关的c语法 4.将递归的数学模型写成编程语言 5.利用类比方法将实际问题的代码写成函数递归的形式 例1: 例2: 6.汉诺塔问题的求解 1.前言 本人在学习函数递归编程方法的过程中,发现用类比的方式学习递归法可帮助我们在各种编…...

【云原生之Docker实战】使用Docker部署Taskover开源个人任务管理工具
【云原生之Docker实战】使用Docker部署Taskover 开源个人任务管理工具 一、Taskover介绍1.Taskover 简介2.Taskover功能二、检查本地docker环境1.检查系统版本2.检查docker版本3.检查docker状态4.检查docker compose版本三、下载Taskover镜像四、部署Taskover应用1.创建安装目录…...

5、SQL编程开发与注意事项
1.1 导入数据 导入测试库: 文档地址: https://dev.mysql.com/doc/employee/en/sakila-structure.html下载地址: https://github.com/datacharmer/test_db导入测试库: mysql -uroot -p -S < employees.sql 1.2 库操作 增:create database test character set utf8;删:d…...
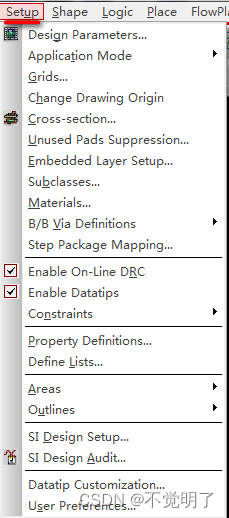
Allegro如何通过视图显示区分动态和静态铜皮操作指导
Allegro如何通过视图显示区分动态和静态铜皮操作指导 用Allegro做PCB设计的时候,通常动态和静态铜皮是无法通过视图显示区分的,只能通过show element查看得知,如下图 左边铜皮是动态铜皮,右边是静态铜皮 但Allegro可以通过一些设置让动静态铜皮以不同效果显示出来 具体操…...

测试开发之Django实战示例 第十一章 渲染和缓存课程内容
第十一章 渲染和缓存课程内容在上一章中,使用了模型继承和通用关系建立弹性的课程、章节和内容的关联数据模型,并且建立了一个CMS系统,在其中使用了CBV,表单集和AJAX管理课程内容。在这一章将要做的事情是:创建公开对外…...
90%企业在探索的敏捷开发怎么做?极狐GitLab总结了这些逻辑与流程
本文来自: 彭亮 极狐(GitLab) 高级产品经理 毛超 极狐(GitLab) 研发工程师 极狐(GitLab) 市场部内容团队 “敏捷” 是指能够驾驭变化,保持组织竞争优势的一种能力。自 2001 年《敏捷宣言》以来,敏捷及敏捷开发理念逐渐席卷全球。中国信通院《…...

LeetCode-257. 二叉树的所有路径
目录题目分析递归法题目来源 257. 二叉树的所有路径 题目分析 前序遍历以及回溯的过程如图: 递归法 1.递归函数参数以及返回值 要传入根节点,记录每一条路径的path,和存放结果集的result,这里递归不需要返回值,代…...

测试用例该怎么设计?—— 日常加更篇(下)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:【Austin_zhai】 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能,分享行业相关最新信息。…...

Java基础:接口
1.接口的概念 当不是所有子类, 而是多个子类都包含一个方法时, 为了代码书写规范性, 可以用自定义的接口来统一该方法的书写规范. 所以接口可以看作是一种书写规则. 接口是对行为的抽象 抽象类一般是书写在父类当中, 接口是单独书写的, 不是一种类 2.接口的定义和使用 3.接口…...

vuex基础入门:uniapp实现用户登录授权实战
1.背景 vuex是数据共享方案之一,本文以微信小程序登录授权为例介绍一下vuex常用属性state、getters、mutations、actions. 2.基于uniapp实现微信小程序登录授权流程 1.凡是需要用户登录授权信息的页面创建时created方法中需要判断用户是否登录,需要使用本地缓存的token调用服务…...

Windows系统从权限维持角度进行应急响应
一、基本介绍 红队攻击者在对目标进行渗透利用后通常都会进行权限维持,以达到持续利用的目的。而作为防守方进行应急响应时,应该如何与技术高超(jiaohuajianzha)的攻击者斗智斗勇呢?或许可以通过本文可以找到答案。以…...

什么是DNS解析?如何提升DNS解析安全?
DNS解析是保障网站正常运行的一项重要服务,DNS解析出现故障,就会导致网站无法被访问或者被劫持到其他的站点,对业务正常开展造成很大影响,因此网站管理人员要高度关注DNS解析的安全,才能确保网站的正常运转,…...

电路学习笔记
电源部分 2s锂电池 6.4v-8.4v INA180A2IDBVR 电流检测放大器 OUT ADC1_CH0 to ESP32 可能功能:电源电流监测 稳压/电压监测 OUT ADC1_CH1 to ESP32 降压至2.046v-2.686v并通过电容保持稳定 可能功能:降压模块,电压监测 LDO ASM1117-3.3 低压差线性…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...
