剑指offer -- 二维数组中的查找
二维数组中的查找_牛客题霸_牛客网 (nowcoder.com)

暴力查找法:
是一种简单直接的解决方法,可以用于在二维数组中查找目标值。该方法的思路是遍历数组的每个元素,逐个与目标值进行比较。
具体步骤如下:
- 从数组的第一行第一列开始,逐行逐列地遍历数组的每个元素。
- 对于当前遍历到的元素,与目标值进行比较:
- 如果当前元素等于目标值,则找到目标值,返回true。
- 如果当前元素大于目标值,则可以提前结束查找,因为数组已经按递增顺序排列,后续元素必定更大。
- 如果遍历完整个数组都没有找到目标值,则说明目标值不存在于数组中,返回false。
- 时间复杂度为O(m * n)
bool searchMatrix(vector<vector<int>>& matrix, int target) {for (int i = 0; i < matrix.size(); i++) {for (int j = 0; j < matrix[i].size(); j++) {if (matrix[i][j] == target) {return true; // 找到目标值} else if (matrix[i][j] > target) {return false; // 提前结束查找}}}return false; // 目标值不存在于数组中 }
对于有序的二维数组,我们可以利用二分查找法进行查找目标值。
算法步骤:
1. 初始化指针,将左上角的元素作为起始点,将右下角的元素作为终止点。初始时,起始点为数组的左上角元素,终止点为数组的右下角元素。
2. 在每一次迭代中,将搜索区域一分为二,找到中间元素(可以选择行中间或列中间的元素)。
3. 将目标值与中间元素进行比较:
- 如果中间元素等于目标值,则找到目标值,返回true。
- 如果中间元素大于目标值,则目标值可能在中间元素的左侧或上方,将搜索区域缩小为左上方的子区域,即终止点变为中间元素的左上方元素。
- 如果中间元素小于目标值,则目标值可能在中间元素的右侧或下方,将搜索区域缩小为右下方的子区域,即起始点变为中间元素的右下方元素。
4. 重复执行步骤2和步骤3,直到找到目标值或搜索区域为空(起始点超过终止点)为止。
5. 如果最终搜索区域为空,说明目标值不存在于数组中,返回false。6.时间复杂度(cols*log(rows))
bool searchMatrix(vector<vector<int>>& matrix, int target) {if (matrix.empty() || matrix[0].empty()) {return false; // 处理空数组的情况}int rows = matrix.size();int cols = matrix[0].size();int left = 0;int right = rows * cols - 1;while (left <= right) {int mid = left + (right - left) / 2;int midValue = matrix[mid / cols][mid % cols];if (midValue == target) {return true; // 找到目标值} else if (midValue < target) {left = mid + 1; // 目标值可能在中间元素的右侧或下方} else {right = mid - 1; // 目标值可能在中间元素的左侧或上方}}return false; // 目标值不存在于数组中 }
题目要求在一个二维数组中查找是否存在某个整数。该二维数组的特点是每一行从左到右递增,每一列从上到下递增。
解决该问题的一个思路是从二维数组的右上角开始比较,根据目标值与当前元素的大小关系,可以逐步缩小查找范围。具体步骤如下:
- 初始化指针
row为0,指向第一行的最后一个元素,指针col为二维数组的列数减1,指向最后一列的第一个元素。- 进入循环,比较当前指针指向的元素
array[row][col]与目标值target的大小关系:
- 如果
array[row][col]等于target,说明找到了目标值,返回True。- 如果
array[row][col]大于target,说明目标值可能在当前元素的左侧,将指针col向左移动一列。- 如果
array[row][col]小于target,说明目标值可能在当前元素的下方,将指针row向下移动一行。- 如果指针
row或col超出了二维数组的边界,则说明查找范围已经越界,目标值不存在于二维数组中,返回False。- 空间复杂度O(m+n)
#include <iostream> #include <vector>using namespace std;bool findTarget(vector<vector<int>>& array, int target) {if (array.empty() || array[0].empty()) {return false;}int rows = array.size();int cols = array[0].size();int row = 0;int col = cols - 1;while (row < rows && col >= 0) {if (array[row][col] == target) {return true;} else if (array[row][col] > target) {col--;} else {row++;}}return false; }int main() {vector<vector<int>> array = {{1, 2, 8, 9},{2, 4, 9, 12},{4, 7, 10, 13},{6, 8, 11, 15}};int target1 = 7;int target2 = 3;cout << boolalpha << findTarget(array, target1) << endl; // 输出: truecout << boolalpha << findTarget(array, target2) << endl; // 输出: falsereturn 0; }
相关文章:

剑指offer -- 二维数组中的查找
二维数组中的查找_牛客题霸_牛客网 (nowcoder.com) 暴力查找法: 是一种简单直接的解决方法,可以用于在二维数组中查找目标值。该方法的思路是遍历数组的每个元素,逐个与目标值进行比较。 具体步骤如下: 从数组的第一行第一列开始,…...
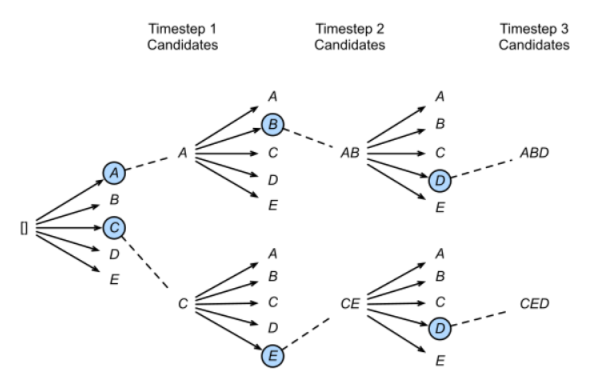
3. 自然语言处理NLP:具体用途(近义词类比词;情感分类;机器翻译)
一、求近义词和类比词 1. 近义词 方法一:在嵌入模型后,可以根据两个词向量的余弦相似度表示词与词之间在语义上的相似度。 方法二:KNN(K近邻) 2. 类比词 使用预训练词向量求词与词之间的类比关系。eg:man&a…...

Hibernate的FlushMode
一、Session中FlushMode的设置: 在事务开启前设置FlushMode属性,方法: // session.setFlushMode(FlushMode.Always|AUTO|COMMIT|NEVER|MANUAL)。Service public class TestService {Logger log LoggerFactory.getLogger(getClass());AutowiredEntityM…...

二线程序员的出路
最近长沙不太平。去年被动离职一拨人之后,HR一直强调降本增效,人人自危,挤走一拨人,反正会有大量内卷失败的一线程序员进来填坑。当然留就有人走,前同事除了几个出去搞培训创业(后面解散了)的之…...

MKS SERVO4257D 闭环步进电机_系列2 菜单说明
第1部分 产品介绍 MKS SERVO 28D/35D/42D/57D 系列闭环步进电机是创客基地为满足市场需求而自主研发的一款产品。具备脉冲接口和RS485/CAN串行接口,支持MODBUS-RTU通讯协议,内置高效FOC矢量算法,采用高精度编码器,通过位置反馈&am…...
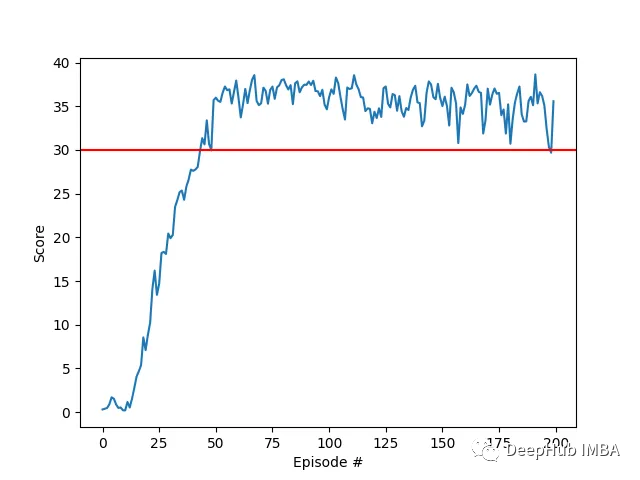
使用Actor-Critic的DDPG强化学习算法控制双关节机械臂
在本文中,我们将介绍在 Reacher 环境中训练智能代理控制双关节机械臂,这是一种使用 Unity ML-Agents 工具包开发的基于 Unity 的模拟程序。 我们的目标是高精度的到达目标位置,所以这里我们可以使用专为连续状态和动作空间设计的最先进的Deep…...

黑马学生入职B站1年,晒出21K月薪:我想跳槽华为
现在的Z时代,嘴上说着不要,身体却很诚实。 前两天,黑马发布了《2022年度互联网平均薪资出炉!高到离谱!》,信息传输、软件和信息技术服务业薪资遥遥领先!Z时代举头望着天花板,故作潇…...

一文看懂GPT风口,都有哪些创业机会?
新时代的淘金者,低附加价值的创业要谨慎,高附加价值、低技术门槛创业也要谨慎,主干道边上的创业也要谨慎。不少朋友看完不淡定了,干什么都谨慎,回家躺平好了,我有个朋友,靠ChatGPT,半…...

chatgpt赋能python:Python中的不确定尾数问题
Python中的不确定尾数问题 Python作为一种高级编程语言,被广泛应用于数据科学、机器学习、Web开发等众多领域。然而,Python在处理浮点数时会出现一些不确定尾数的问题,给程序员和数据分析员带来不少麻烦。本篇文章将介绍Python中不确定尾数的…...
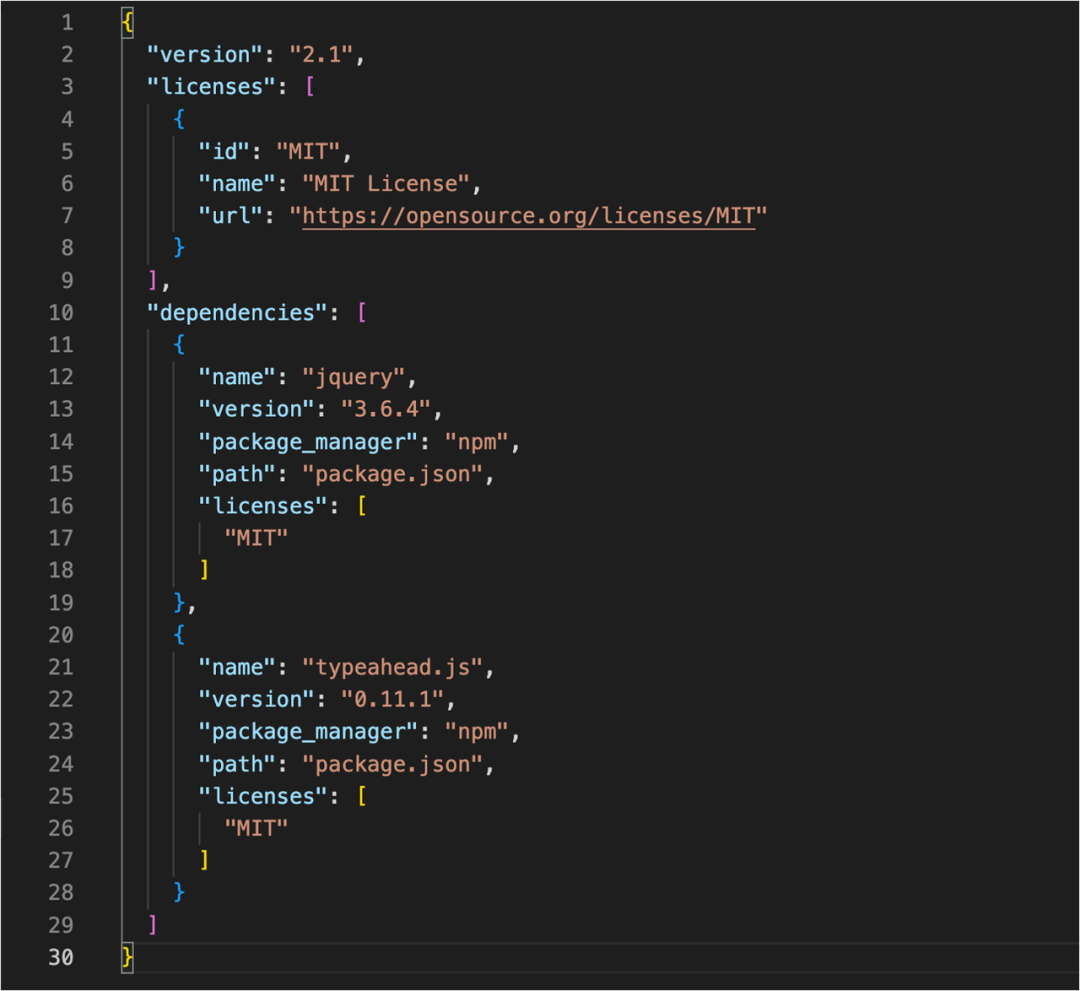
杜绝开源依赖风险,许可证扫描让高效合规「两不误」
目录 开源许可证及其常见类型 开源许可证扫描是软件研发过程中,不可或缺的工具 极狐GitLab 开源许可证扫描的优势与应用 Step 1:启用及设置许可证策略 Step 2:自动创建策略文件存放项目 Step 3:查看许可证合规情况 Step 4&…...
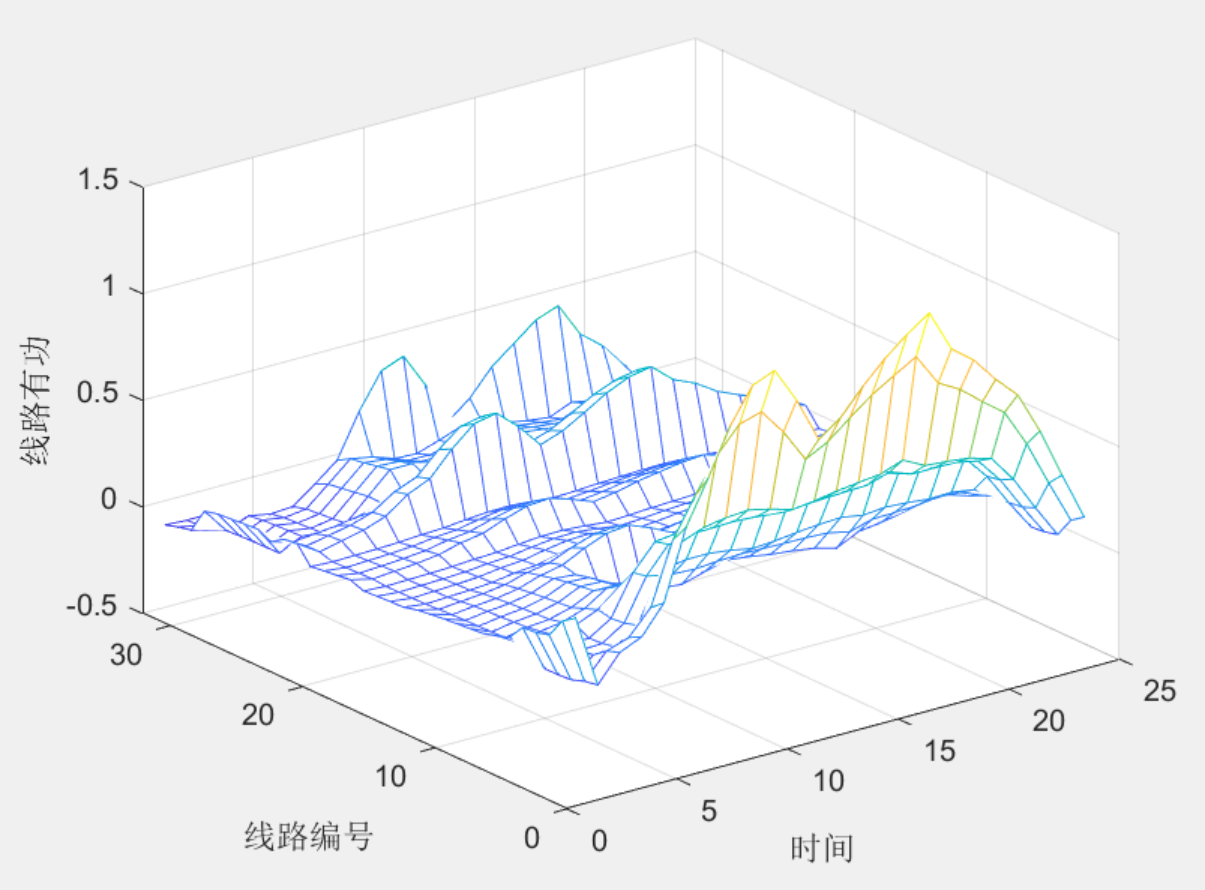
【sop】含储能及sop的多时段配网优化模型
目录 1 主要内容 2 部分代码 3 程序结果 4 下载链接 1 主要内容 之前分享了含sop的配电网优化模型,链接含sop的配电网优化,很多同学在咨询如何增加储能约束,并进行多时段的优化,本次拓展该部分功能,在原代码的基础上增加储能模…...

nodjs使用阿里云镜像安装
要使用阿里云镜像来安装 npm 包,你需要按照以下步骤进行操作: 首先,确保你已经安装了 Node.js 和 npm。你可以在终端(或命令提示符)中输入以下命令来验证它们的安装: node -v npm -v如果显示了 Node.js 和…...
C++ Primer Plus 第二章习题
目录 复习题 1.C程序的模块叫什么? 2.#include 预处理器编译指令的用处? 3.using namespace std; 该语句是干什么用的? 4.什么语句可以打印一个语句"hello,world",然后重新换行? 5.什么语句可以用来创…...

两分钟学会 制作自己的浏览器 —— 并将 ChatGPT 接入
前期回顾 分享24个强大的HTML属性 —— 建议每位前端工程师都应该掌握_0.活在风浪里的博客-CSDN博客2分享4个HTML5 属性,开发必备https://blog.csdn.net/m0_57904695/article/details/130465836?spm1001.2014.3001.5501 👍 本文专栏:开发…...

HEVC中,mvd怎么写进码流的?
文章目录 Motion vector difference syntax 标准文档描述语义解释设计意义 Motion vector difference syntax 标准文档描述 语义解释 MvdL1[ x0 ][ y0 ][ compIdx ] L1列表的mvd x0,y0 表示亮度快左上角坐标 compIdx 0表示水平 compIdx 0表示垂直 mvd_l1_zero_flag:…...

隐形黑客潜入美国和关岛关键基础设施而未被发现
微软和“五眼联盟”国家周三表示,一个隐秘的组织成功地在美国和关岛的关键基础设施组织中建立了一个持久的立足点,而没有被发现。 这家科技巨头的威胁情报团队正在以伏特台风(Volt Typhoon)的名义跟踪这些活动,包括入侵后的凭证访问和网络系…...
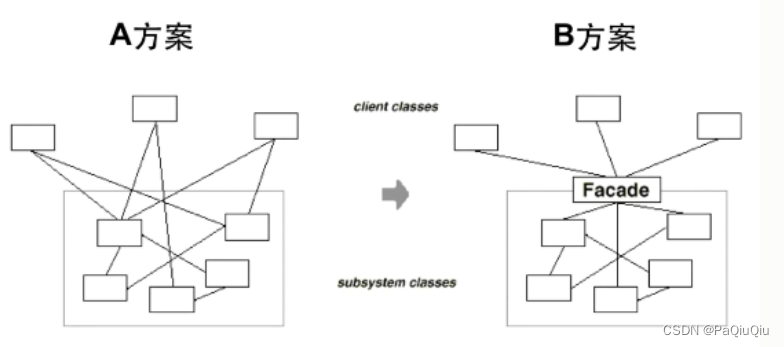
设计模式—“接口隔离”
在组件构建过程中,某些接口之间直接的依赖常常会带来很多问题、甚至根本无法实现。采样添加一层间接(稳定)接口,来隔离本来互相紧密关联的接口是一种常见的解决方案。 典型模式有:Fascade、Proxy、Adapter、Mediator 一、Fascade 动机 上述A方案的问题在于组件的客户和…...
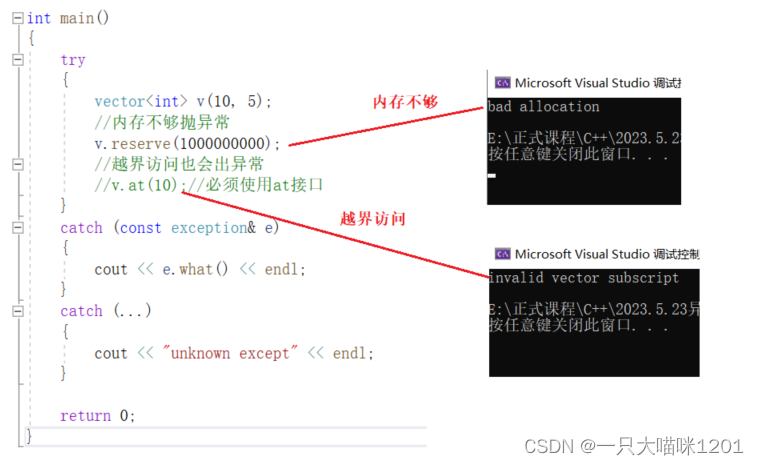
【C++学习】异常
🐱作者:一只大喵咪1201 🐱专栏:《C学习》 🔥格言:你只管努力,剩下的交给时间! 异常 🥮异常🍢自定义异常体系🍢C标准库的异常体系🍢异…...

如何理解TCP是面向字节流协议?
传输层是网络协议中的重要层次之一,主要负责向两个主机中的进程之间的通信提供服务。传输层的主要功能包括复用和分用、流量控制、分段/重组和差错控制。传输层在终端用户之间提供透明的数据传输,向上层提供可靠的数据传输服务。 传输层的复用和分用功能…...
机器学习期末复习 线性模型
1.线性回归,对数几率回归,线性判别分析是分类还是回归任务?是有监督的学习还是无监督的学习? 有监督学习和无监督学习 解释: 线性模型要做的有两类任务:分类任务、回归任务 分类的核心就是求出一条直线w…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
