中介效应分析全流程汇总
一、中介效应说明
中介效应主要研究自变量对因变量影响的过程中,自变量是否通过中介变量再对因变量产生影响,那什么情况表明中介效应存在呢?如果自变量对因变量影响过程中,中介变量在模型中有着桥梁般的作用,那说明中介效应存在。比如在电商数据中,经济发展水平通过影响居民收入从而影响电子商务。模型如下:

二、中介效应常见类型
中介效应常见有两种类型,一种是平行中介一种是链式中介,平行中介:一般是指多个中介变量在自变量对因变量的影响中起着同等重要的作用,中介变量之间互不影响,比如经济发展水平通过影响居民收入从而影响电子商务,经济发展水平还可以通过影响消费能力进而影响电子商务,则模型一般如下:

链式中介:一般指几个中介变量在自变量对因变量的影响中起着一样的中介作用,到那时中介变量之间相互影响,一般模型如下:

三、数据类型及操作
一般数据有两种类型一个是定类变量一个是定量变量,通常中介作用的中介变量和自变量均为定量变量,如果自变量为定类变量怎么办?可以将自变量进行哑变量处理,处理后需要在分析时少放入一项作为参考项。进行中介效应分析,可以使用SPSSAU中的中介作用进行分析,或者使用分层回归进行研究。
中介作用:
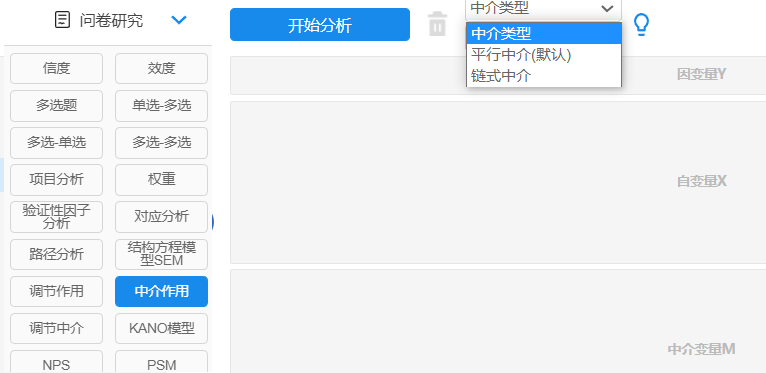
分层回归分析:

四、分析中常见步骤
1、数据处理
此步骤通常是对自变量、因变量、中介变量做标准化处理,有时也使用中心化处理。标准化处理和中心化处理的主要目的是为了减少多重共线性。此步骤可以在SPSSAU中数据处理模块的生成变量进行处理,有时研究者的变量是由多个题项组成,而中介作用并不是对题项进行研究而是对变量进行研究,所以需要先进行计算对应题项的平均得分,并以平均得分代表对应的变量。比如幸福感变量由3个题项表述,则应该计算3个题项的平均分进行表示该变量。
2、分析第一个模型
第一个模型针对自变量对因变量的回归关系进行分析。比如例子中的经济发展水平对电子商务的影响,一般称为总效应,其模型公式一般为:Y=cX+e1(其中c代表自变量对因变量的回归系数,e1代表残差);

3、分析第二个模型
第二个模型是在第一个模型基础上加入中介变量,也就是自变量和中介变量对因变量分层回归。其模型公式一般为:Y=c’X+bM+e2(c’代表此模型中X对Y的回归系数一般称为直接效应,b代表M对Y的回归系数,e2代表此模型的残差);

4、分析第三个模型
第三个模型为自变量对中介变量的回归分析,其一般式为M=aX+e3(a代表X对M的回归系数,e3代表残差);

5、进行中介效应分析
(1)最后进行中介效应分析,首先查看第一个模型的系数c如果不显著,则说明自变量对因变量没有影响,如果显著说明自变量对因变量有影响,进一步分析。
(2)然后进行查看模型2的系数b和模型3的系数a,如果a和b均显著,则查看模型3的系数c’, c’显著则为部分中介,c’不显著则为完全中介。
(3)如果a和b至少一个不显著,则进行sobel检验,sobel检验显著则为部分中介,如果sobel检验不显著则没有中介作用。(sobel检验请参考:http://quantpsy.org/sobel/sobel.htm)
此种方法简单易懂,、容易理解和解释,因而受到广泛的应用,但有学者认为其检验效能较低,有时候本身有中介作用但却显示没有中介作用。因为有学者将检验流程进行优化:
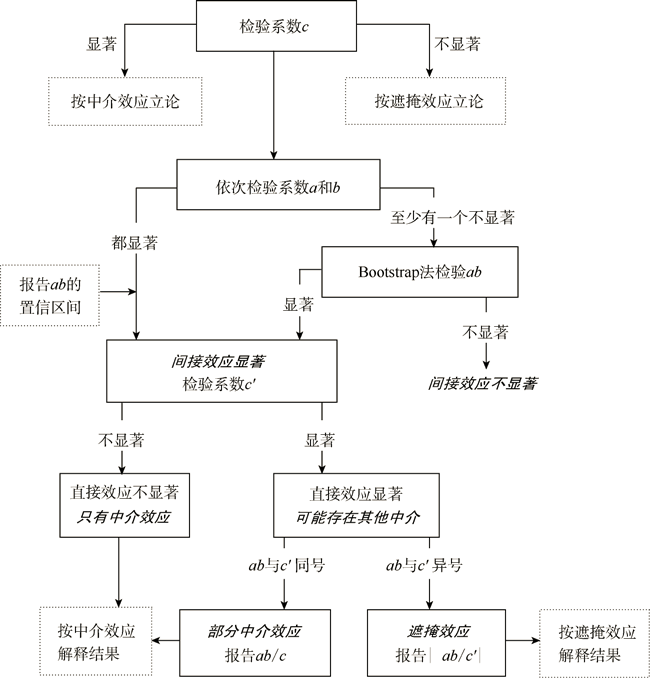
图表解说:
上图中回归系数a和回归系数b的乘积项(a*b)称为间接效应,如果其呈现出显著性,那么就说明具有中介作用,反之不具有显著性,则说明不具有中介作用。检验a*b的显著性用于判断是否具有中介作用,这种做法即称为乘积系数检验法。而具体Bootstrap抽样法检验是指a*b这个回归系数的95%置信区间是否包括数字0;如果说95%置信区间不包括数字0,则说明具有中介作用;如果说95%置信区间包括数字0,即说明没有中介作用。所以具体说明如下:
第一:c表示X对Y时的回归系数(模型中没有中介变量M时),即总效应;
第二:a表示X对M时的回归系数,b表示M对Y时的回归系数,a*b为a与b的乘积即中介效应;
第三:95% BootCI表示Bootstrap抽样计算得到的95%置信区间,如果区间不包括0则说明显著;
第四:c’表示X对Y时的回归系数(模型中有中介变量M时),即直接效应;
第五:如果a和b显著,且c’不显著,则为完全中介;
第六:如果a和b显著,且c’显著,且a*b与c’同号,则为部分中介作用;
第七:如果a和b显著,且c’显著,且a*b与c’异号,则为遮掩作用;
第八:如果a和b至少一个不显著,且a*b的95% BootCI包括数字0(不显著),则中介作用不显著;
第九:如果a和b至少一个不显著,且a*b的95% BootCI不包括数字0(显著),且c’不显著,则为完全中介;
第十:如果a和b至少一个不显著,且a*b的95% BootCI不包括数字0(显著),且c’显著,且a*b与c’同号,则为部分中介作用;
第十一:如果a和b至少一个不显著,且a*b的95% BootCI不包括数字0(显著),且c’显著,且a*b与c’异号,则为遮掩作用;
五、中介效应分析
接下来举例进行分析中介效应,以进行优化过得流程为参考。案例背景:某公司想要研究个人发展、工作特性、工作回报是否通过团队合作对创新绩效产生影响。其中个人发展、工作特性、工作回报为自变量,团队合作为中介变量,创新绩效为因变量。操作如下:

结果如下:
首先查看中介作用的三个模型以及系数,如下表:
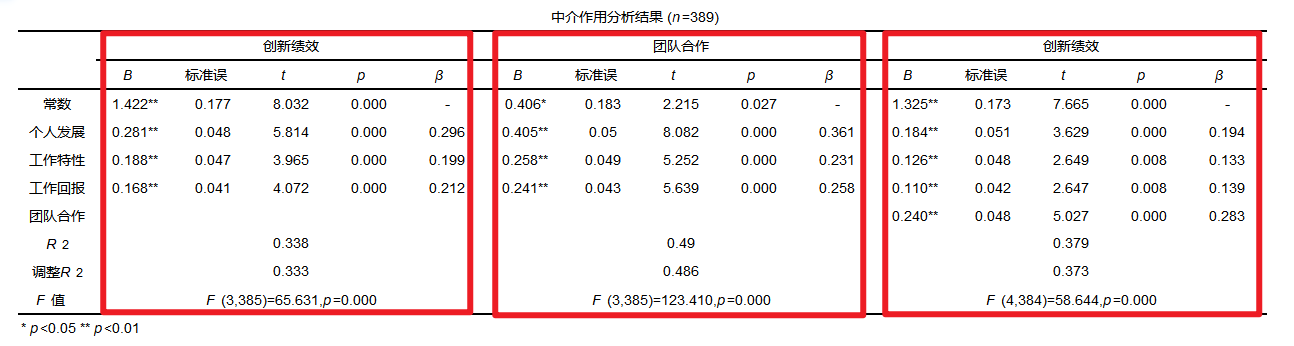
从上表可知:中介效应分析共涉及3个模型,分别如下:
创新绩效=1.422+0.281*个人发展+0.188*工作特性+0.168*工作回报
团队合作=0.406+0.405*个人发展+0.258*工作特性+0.241*工作回报
创新绩效=1.325+0.184*个人发展+0.126*工作特性+0.110*工作回报+0.240*团队合作
接下来查看中介效应的结果,如下表:

- 个人发展→团队合作→创新绩效
上表得知总效应c显著,并且系数a和系数b均显著,且与c’同号(都大于0)则为部分中介。 - 工作特性→团队合作→创新绩效
上表得知总效应c显著,并且系数a和系数b均显著,且与c’同号(都大于0)则为部分中介。 - 工作回报→团队合作→创新绩效
上表得知总效应c显著,并且系数a和系数b均显著,且与c’同号(都大于0)则为部分中介。
得到的中介效应量如下:
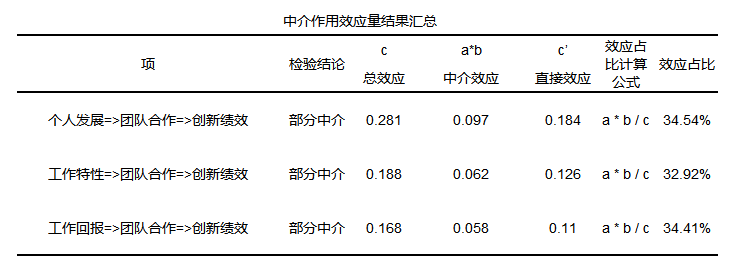
效应量计算说明如果是完全中介,则效应占比为100%,如果是部分中介,则效应占比计算公式为:a*b/c,如果是遮掩效应,则效应量为中介效应与直接效应的比值,计算公式为:| a*b/c |。
六、疑难解惑
1.95%区间包括0,为什么显示有中介作用?
中介作用分析有着非常严格的检验流程,绝大多数情况下,95%抽样区间不包括数字0就意味着具有中介作用,但并不完全是这样,最终中介作用的检验需要参考检验流程进行。
2. 面板数据是否可以进行中介作用?
从数学理论上,面板数据可以直接进行中介作用分析,中介作用分析并不区分是否面板数据,直接分析即可。
3.间接效应和中介效应的区别是什么?
通常情况下二者意义完全一致,但细微区别在于比如X->M1->M2->Y这种链式中介时,一般用间接效应描述会更易理解。
相关文章:

中介效应分析全流程汇总
一、中介效应说明 中介效应主要研究自变量对因变量影响的过程中,自变量是否通过中介变量再对因变量产生影响,那什么情况表明中介效应存在呢?如果自变量对因变量影响过程中,中介变量在模型中有着桥梁般的作用,那说明中…...
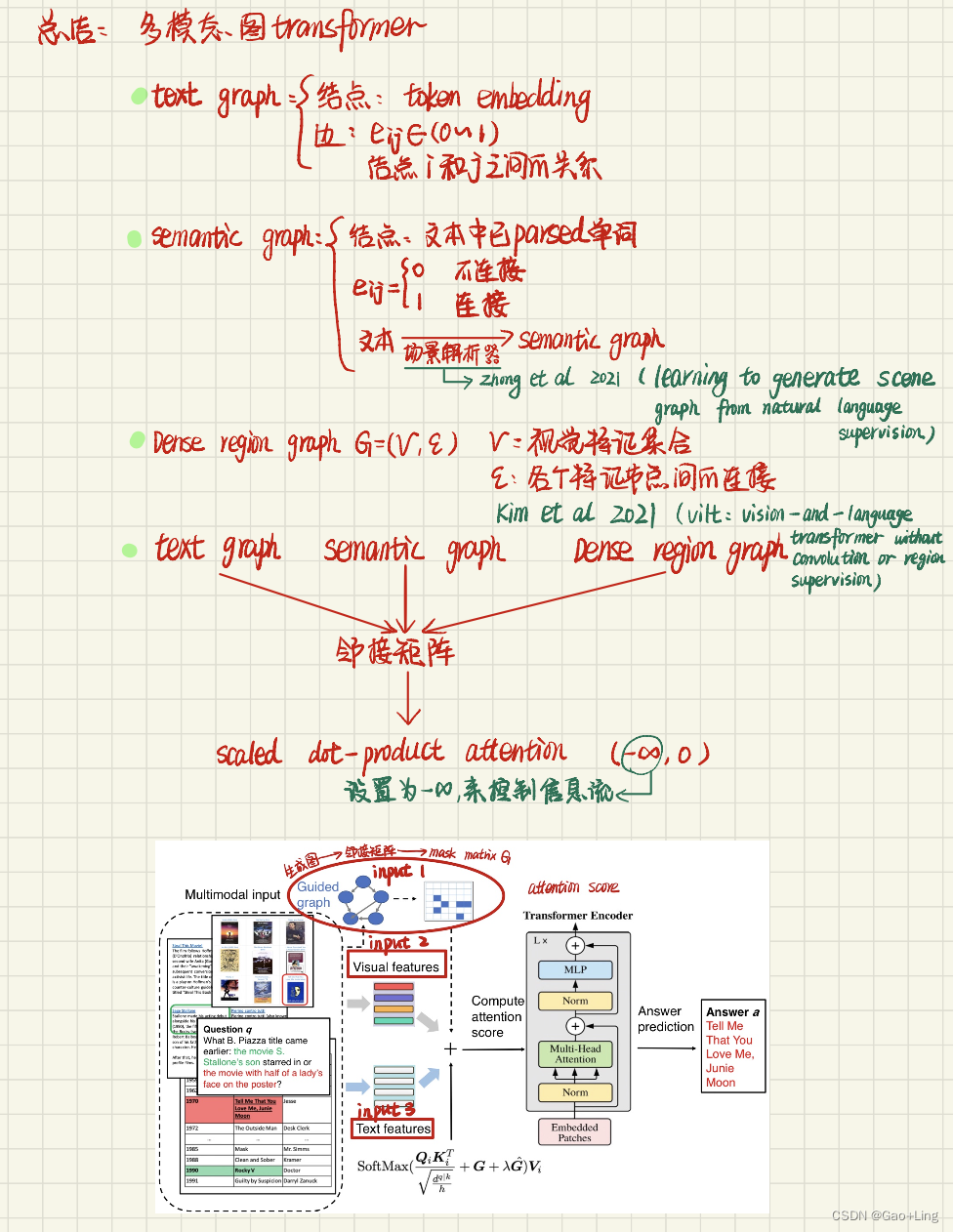
论文阅读:Multimodal Graph Transformer for Multimodal Question Answering
文章目录 论文链接摘要1 contribution3 Multimodal Graph Transformer3.1 Background on Transformers3.2 Framework overview 框架概述3.3 Multimodal graph construction多模态图的构建Text graphSemantic graphDense region graph Graph-involved quasi-attention 总结 论文…...
 函数简单实用示例)
关于compile() 函数简单实用示例
compile() 函数是什么 compile() 函数将一个字符串编译为字节代码。 compile将代码编译为代码对象,应用在代码中可以提高效率。 语法 compile(source, filename, mode, flags0, dont_inheritFalse, optimize-1) 参数 source:表示要编译的源代码字符串、…...

Deep Frequency Filtering for Domain Generalization论文阅读笔记
这是CVPR2023的一篇论文,讲的是在频域做domain generalization,找到频域中generalizable的分量enhance它,suppress那些影响generalization的分量 DG是一个研究模型泛化性的领域,尝试通过各自方法使得模型在未见过的测试集上有良好…...
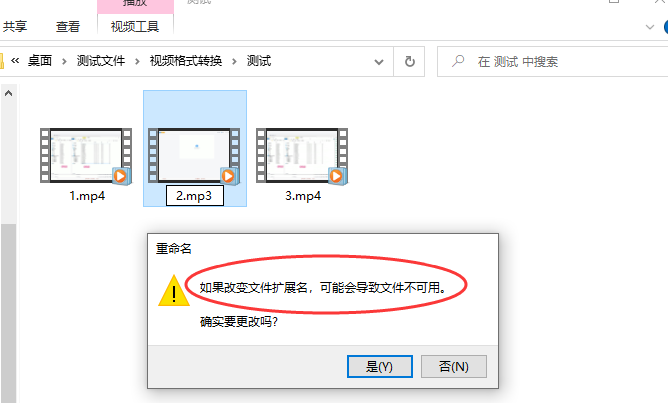
视频里的声音怎么转换成音频?
视频里的声音怎么转换成音频?这样我们就能把视频里的想要的声音在其他音频平台播放或是用于其他视频。其实视频提取音频是一种将视频文件中的音频数据分离出来的技术。该技术可以将视频中的音频转换为不同的格式,让我们可以在无需视频的情况下使用音频文…...

1.1. Java简介与安装
Java简介 Java是一种广泛使用的计算机编程语言,由James Gosling和他的团队在Sun Microsystems公司开发,于1995年首次发布。Java的设计理念是“一次编写,到处运行”,这意味着Java应用程序可以在任何支持Java运行时环境(…...
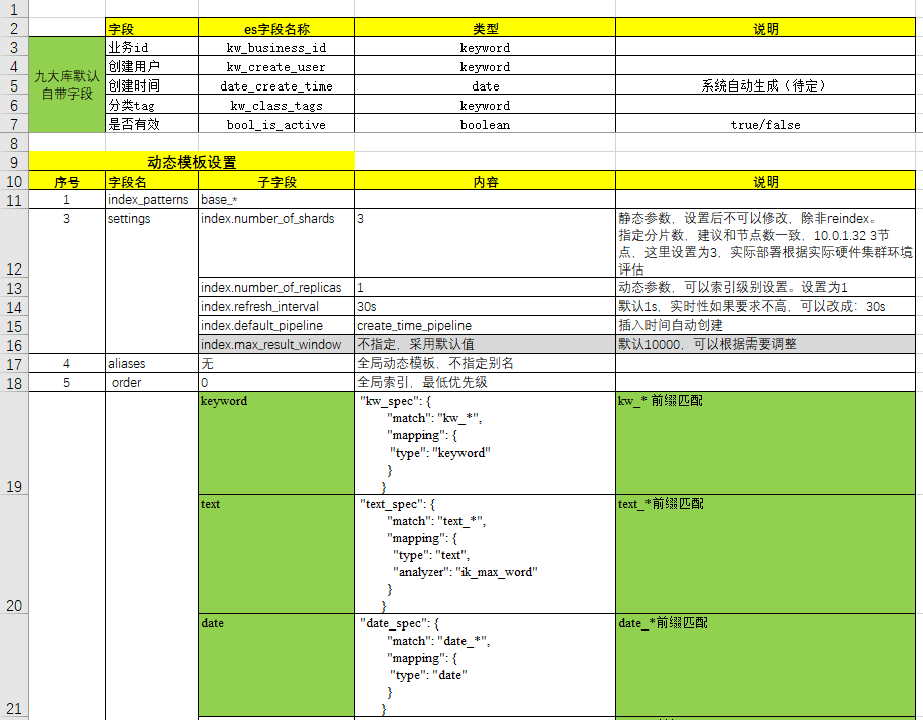
Elasticsearch 8.X 性能优化参考 —— 筑梦之路
Elasticsearch 是实现用户无缝搜索体验的关键工具。它通过提供快速、准确和相关的搜索结果,彻底改变了用户与应用程序的互动方式。然而,要确保 Elasticsearch 部署达到最佳性能,就必须关注关键指标,并对诸如索引、缓存、查询、搜索…...

通过强化学习走直线理解基本概念
摘要: 一条线上包含起点和终点共有6个格子,起点在左终点在右。假设智能体已经学到了最优的策略,并且在每一步行动时,以 0.9 0.9 0.9 的概率选择最优策略(也就是往右),以 0.1 0.1 0.1 的概率选…...

Java字符流
5 字符流 5.1 为什么出现字符流 由于字节流操作中文不是特别的方便,所以Java就提供字符流字符流=字节流+编码表用字节流复制文本文件时,文本文件也会有中文,但是没有问题,原因是最终底层操作会自动进行字节拼接成中文,如何识别是中文的呢? 汉字在存储的时候, 无论选择哪…...

2023年上半年信息系统项目管理师上午真题及答案解析
1.“新型基础设施”主要包括信息技术设施、融合基础设施和创新基础设施三个方面。其中信息基础设施包括( )。 ①通信基础设施 ②智能交通基础设施 ③新技术基础设施 ④科教基础设施 ⑤算力基础设施 A.①③⑤ B.①④⑤ C.②③④ D.②…...

LeetCode 739 每日温度
题目: 给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。 示例 1…...
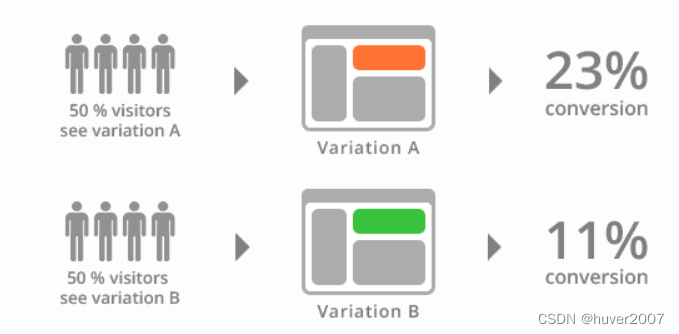
介绍几种常见的运维发布策略
随着Devops的发展,为了提高运维发布的成功率,探索出了多种发布策略。本文简单介绍几种常见发布策略, 以及它们适用的场景和优缺点。 第一种,停机发布 这是最早的一种发布策略,停机发布会在发布以前关闭服务,停止用户…...

C++ QT QDBus进阶用法。
以下是使用QDBus的高级用法示例代码: 1. 使用DBus的异步调用机制: #include <QCoreApplication> #include <QDebug> #include <QDBusConnection> #include <QDBusPendingCallWatcher> class MyDBusObject : public QObject …...
)
2023-5-26 LeetCode每日一题(二进制矩阵中的最短路径)
2023-05-29每日一题 一、题目编号 1091. 二进制矩阵中的最短路径二、题目链接 点击跳转到题目位置 三、题目描述 给你一个 n x n 的二进制矩阵 grid 中,返回矩阵中最短 畅通路径 的长度。如果不存在这样的路径,返回 -1 。 二进制矩阵中的 畅通路径…...

博客系统后端设计(七) - 实现显示用户信息与注销功能
文章目录 1. 显示用户信息1.1 约定前后端交互接口1.2 修改列表页的前段代码1.3 实现详情页的后端代码1.4 实现详情页的前端代码 2. 注销2.1 确定前后端交互接口2.2 实现后端代码2.3 修改前端代码 1. 显示用户信息 此处的用户名是写死的,我们希望的是此处是能够动态生…...
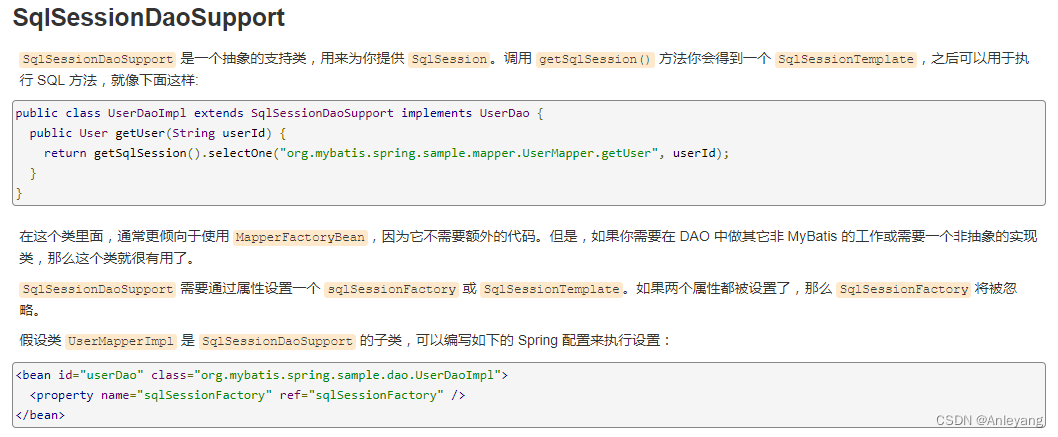
Spring5 学习笔记
前置知识: 掌握Java基础知识(特别是反射)掌握Java注解掌握XML掌握Maven Spring5学习笔记 1、Spring概述1.1、简介1.2、优点1.3、组成1.4、拓展 2、IOC理论推导2.1、分析实现2.2、IOC本质 3、HelloSpring3.1、导入jar包3.2、编写代码3.3、思考…...

leetcode--分隔链表(java)
分割链表 leetcode 86 分割链表 (中等)解题思路:链表专题 leetcode 86 分割链表 (中等) leetcode 86 分割链表 原题链接,可以直接测试 给你一个链表的头节点 head 和一个特定值 x ,请你对链表进…...

使用 AD8232 ECG 传感器和 ESP32 进行基于物联网的 ECG 监测
这篇文章是使用 AD8232 ECG 传感器和 ESP32 进行基于物联网的 ECG 监测。可以从世界任何地方在线观察来自患者心脏的心电图信号。 目录 概述 什么是心电图? 心电图的医疗用途 AD8232 心电图传感器...

【Linux初阶】基础IO - 文件操作(使用系统接口实现) | vim批量注释代码
🌟hello,各位读者大大们你们好呀🌟 🍭🍭系列专栏:【Linux初阶】 ✒️✒️本篇内容:重新理解文件和文件操作,C语言实现的简单文件操作,文本初始权限,系统接口介…...

网络安全之信息收集
第一部分:被动信息收集 1、简介 在信息收集这块区域,我将其分为两部分:第一部分即被动信息收集,第二部分即主动信息收集。 对于标准的渗透测试人员来说,当明确目标做好规划之后首先应当进行的便是信息收…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...
