cf1200构造15道
最近做构造,想对比下先做后看答案归纳,留下思路之后直接看答案归纳,然后再统一检测,还有直接看答案,归纳,检测三种方法哪种效率高些,于是先做个十五题试试第一个方法,花3天写了15道构造,等到归纳的时候已经有点忘了,要看答案来回忆一下,感觉是不如留思路之后对照答案。但是最终还是能归纳出一些简单东西,效果还是可以的。
1.B. Same Parity Summands
Problem - 1352B - Codeforces
#分类构造 #数论 奇奇得奇,奇偶得偶
题目提到:如果有多个答案,请打印其中任何一个,可以考虑构造
已知一个数n,求是否能够把n分解成k个的奇偶性相同的元素
如果k个元素有共同的奇偶性,k个元素相加可以看作是k乘一个奇数或偶数。
且k个元素相加等于n,可以看作k与一个奇数偶数的乘积等于n
因为奇偶数相乘根据情况有不同结果,所以分类构造。
2.B. Sorted Adjacent Differences
Problem - 1339B - Codeforces
#直接构造 #排序
序列构造涉及到大小关系时要排序。
已知n长度的序列,要对这个序列排序使得从第一项到最后一项相邻项差值的绝对值递增。
如果要构造一个相邻项差值递增或递减的序列,可以考虑用一个有序的数组,中间元素往两边差值递增。两边元素向中间差值递减
两边往中间,则两个数的差值越来越小。
3.B1. Palindrome Game (easy version)
Problem - 1527B1 - Codeforces
#回文串 #博弈 #构造 #字符串
有一个字符串,有两种操作,
1.选择一个0变成1,
2.反转这个字符串,如果原本是不回文的。
每次翻转消耗一美元,消耗美元数量少的获胜,求获胜方。
修改回文串单个元素,可以考虑奇数长度时,n/2+1这个元素自己与自己回文这个点。
博弈,从小情况开始讨论,往后的复杂情况可以被拆分成小情况
4.C1. k-LCM (easy version)
Problem - 1497C1 - Codeforces
#最小公倍数 #分组构造 #lcm
三个数相加,和为n;
lcm(a,b,c) <= n/2;
让lcm内的元素满足某条件,可以考虑:
1)元素互质时,lcm等于乘积
2)元素相等
3)元素为1,2,4与其倍数
5.D. Districts Connection
Problem - 1433D - Codeforces
#图论 #归纳构造
有n个地区,属于ai个匪帮,要把这些地区用n-1条无向边连接起来,同一匪帮的两个区域不能直接通过一条边连接,求是否有解决方案。
同一匪帮不能连在一起,则容易想到只有一个匪帮则无解
此时数学归纳,尝试讨论2个匪帮,可以把一个全部连到另一个,然后另一个全部连到前一个。
3个匪帮,因为匪帮间相互独立,所以第3个匪帮也可以实行像第一个匪帮的操作,全部连到另一个匪帮即可。
6.B. Jumps
Problem - 1455B - Codeforces
#归纳构造
对0第i次操作可以+i,或者-1,求得到一个n的最少操作数。
考虑一直+i,直到>=n,然后考虑把其中一些操作换成-1,来凑出一个n
比如如果得到n+2,可以少掉一个+1的操作,然后多一个-1的操作。此时分析这种操作的前提,因为得到的是中间的值,所以要往两边归纳。往后看,因为i的差值只有1的所以可以得到n+3,n+4……n+k。
往前看,得到n +1 时,由于+1已经最小,所以只能另外构造,化成n+2-1的情况,比n+2多一步,要i+1步。
如果是n+1,就只能凑出n+2之后再-1了。
7.D. Corrupted Array
Problem - 1512D - Codeforces — 问题-1512D- Codeforces
#排序 #分类构造
序列构造涉及到大小关系时要排序。
有一个n+2个元素的数组b,这个数组b中
n个元素是a中的元素,1个元素是a的总和,1个是任意加入的元素。
要构造一个a数组
总和一定是比a中所有元素都要大的,
b数组排序之后,就可以把这个总和元素锁定在n+1和n+2的位置,
因为新加入的元素大小未知。所以要讨论
x > sum
x < sum
分类构造,看是否能满足前缀和的要求。
8.C. Mocha and Hiking
Problem - 1559C - Codeforces
#图论 #分类构造
有n+1个村庄,2n-1条有向边,有n-1条是从1连接到n的,其余n条是连接前n个村庄n+1村庄的。
求构造一条路线,经过所有村庄,每个村庄只经过一次。
由于每个村庄只能去一次,且道路是从1到n的,
所以只能从1开始,或者从n+1开始,然后去到1
对于什么时候去n+1,
只有三种情况:
1.直接从1到n,然后去n+1结束,ar[1] = 1
2.从n+1开始,然后去到1,再一直走到n ar[n] = 0;
3.从1开始,中间i点去到n+1,然后返回i+1点。 ar[i] = 0 && ar[i+1] = 1;
发现如果不满足1,且不满足2时,必然会满足3.所以必定有解。
9.C. A-B Palindrome
Problem - 1512C - Codeforces — 问题-1512C- Codeforces
#回文串 #字符串 #模拟 #直接构造
1-n下标回文串模拟时常用i,n-i+1的指针,
回文串构造一般要考虑奇数长度的中间点。
有一个由0,1,?组成的字符串,以及0的个数,1的个数
?是未知的0或1
求是否能构造出满足条件的字符串。首先先判断一遍已知的串是否已经可以确定不是回文串了,
找到数字,然后看另一边是否相同或者为?,如果是?就改成一样的数字,否则如果不相同就无解。
然后,还有一些可以直接消掉的问号要替换成回文的数字。
然后统计处理好的串里的数字数量,直接sa–sb–就行,如果得到了负值就是无解了。
然后遍历字符串,找到?并修改。
上面的操作不用考虑特殊中间点,这里的替换就要了。因为是一边替换,一遍修改数量
可以考虑通过i 是否 = n-i+1来判断是否是中间点。如果此时sa,sb不是奇数的话就是无解了,否则谁大于0谁上。
其他的情况,谁大于2谁上,然后把???为什么是大于2的上,然后把回文串两边都修改了,前面不是已经把已有的数字给减了一遍吗。如果这里修改的一边是数字,一边是?怎么办
这里卡壳了。
回看了一遍题目和代码懂了:前面处理已经把串i和n-i+1回文的形式了,所以这里遇到一个?就可以直接把n-i+1也修改,并且sa-=2;
10.A. Common Prefixes
Problem - 1384A - Codeforces — 问题-1384A- Codeforces
#直接构造 #字符串
有一个长度为n的序列ai,要用小写字母构造n+1个字符串,第i和i+1个字符串的公共前缀长度为ai
首先考虑长度,找到最大的ai,字符串要构造的最大长度就是ai了
i+1个串然后只要在i的基础上,在ai处把字符修改一下就会有一个与i长度为ai的公共前缀。
11.B. Reverse Binary Strings
Problem - 1437B - Codeforces
#直接构造 #字符串
有一个偶数长度的01串,1和0各有n/2个,可以对字串反转,求让串变成101010或101010的交替形
式的最小操作次数。
翻转操作,只有两端的元素排列会被改变,所以,每次操作必然可以让连续的1或0减少一个长度,然后让一个0和1配对。
总共要配对的次数就是所有1的连续段长度或0连续段长度的最大值。
12.B. Before an Exam
Problem - 4B - Codeforces — 问题-4B- Codeforces
#直接构造
有一个天数,还有一个总学习时长,和每天最大学习时长和最小学习时长限制。
要把学习时长分配到每天,
构造一种方案让每天的学习时长符合要求或无解输出NO
因为数据比较小,只有1e2级别,所以直接让每天的学习时长从最小值开始逐个递增,直到够时长然后打破循环输出。
考虑这种操作的前提条件是总时长在最小学习时长的总和和最大学习时长的总和之间。
13.B. M-arrays
Problem - 1497B - Codeforces — 问题-1497B- Codeforces
#直接构造 #数论
有一个长度为n的数组和一个数m,定义了一个m数组,如果数组里相邻的元素的sum可以被m整除,或者数组只有一个元素,则被称为m数组。要求对数组划分,使得每一个数组都是m数组的最小数组数量。
把数组里的全部元素取余后用哈希统计数量,就得到了方便用来研究整除关系的数据。
首先余数为0的全部分在一个数组ar,如果有则res++
然后遍历1-m/2,如果ar[i] == ar[m-i] ,则这两种情况可以全部放在一个组里。res++,前提条件是ar[i],ar[m-i]存在。
如果ar[i] != ar[m-i] ,则可以分出部分在一个组,因为只是相邻总和被m整除,所以可一个多分一种元素出去。多出来的部分单独成组。res += abs(ar[i] - ar[m-i]);
divisible.可分的
14.B. Paranoid String
Problem - 1694B - Codeforces
#字符串 #归纳构造
当时完全看不懂的题,现在看答案看懂了。
有一个字符串,定义paranoid字符串,一个长度为m的字符串,如果有子串为01就可以把子串替换成1,如果为10就可以把子串替换成0。若可以通过m-1次这样的操作来获得一个长度为1的字符串,就把这个长度为m的字符串叫做paranoid字符串
求给定字符串中有多少个paranoid字符串
首先可以知道长度为1的子串肯定是paranoid字符串,所以字符串有多长就至少会有多少个paranoid字符串
然后增加长度,发现如果新增的数和前一个数不同,包含这个新增数的所有子串就一定是paranoid字符串,
构造出一种操作,遍历字符串,当前ar[i] != ar[i-1],则 += i + 1,就是在原来的基础上再多加一个长度,会新增i + 1个子串。子串数量是1 * 2 * 3 * …… * n + 1(对于0到n-1下标的字符串)
不太确定
否则如果相同的话,就是新增了一个长度为1的子串。
15.B. Prinzessin der Verurteilung
Problem - 1536B - Codeforces
#枚举 #暴力 #字符串
有一个字符串,定义mex为字典序中不是给定字符串子串的第一个字符串,
枚举字符串然后find函数查询就行。
相关文章:

cf1200构造15道
最近做构造,想对比下先做后看答案归纳,留下思路之后直接看答案归纳,然后再统一检测,还有直接看答案,归纳,检测三种方法哪种效率高些,于是先做个十五题试试第一个方法,花3天写了15道构…...

【JavaSE】Java基础语法(十七)
文章目录 1. final2. 代码块2.1 代码块概述2.2 代码块分类 1. final fianl关键字的作用 final代表最终的意思,可以修饰成员方法,成员变量,类 final修饰类、方法、变量的效果 fianl修饰类:该类不能被继承(不能有子类&a…...
《Spring Guides系列学习》guide11 - guide15
要想全面快速学习Spring的内容,最好的方法肯定是先去Spring官网去查阅文档,在Spring官网中找到了适合新手了解的官网Guides,一共68篇,打算全部过一遍,能尽量全面的了解Spring框架的每个特性和功能。 接着上篇看过的gu…...

软件测试面试了一个00后,让我见识到了什么是内卷届的天花板
公司前段缺人,也面了不少测试,结果竟然没有一个合适的。一开始瞄准的就是中级的水准,也没指望来大牛,提供的薪资也不低,面试的人很多,但平均水平很让人失望。令我印象最深的是一个00后测试员,他…...

JAVA BigDecimal 比较大小 、计算
1:比较大小 注意:使用compareTo()方法比较大小时 参与比较的两个值 必须有值 不能为空 BigDecimal a new BigDecimal("3"); BigDecimal b new BigDecimal("4"); if (a.compareTo(b) < 0) { System.…...

并发编程Bug的根源
并发编程Bug的根源 并发编程Bug是指在多线程编程中出现的错误。并发编程需要考虑多个线程同时执行的情况,因此需要特别小心,以避免出现各种问题。在本文中,我们将探讨并发编程Bug的根源,并提供一些例子,以帮助读者更好…...

从零搭建微服务-认证中心(二)
写在最前 如果这个项目让你有所收获,记得 Star 关注哦,这对我是非常不错的鼓励与支持。 源码地址:https://gitee.com/csps/mingyue 文档地址:https://gitee.com/csps/mingyue/wikis 创建新项目 MingYue Idea 创建 maven 项目这…...
面向对象 :模块与包)
python入门(11)面向对象 :模块与包
1. 模块 1.1 什么是模块 在 Python 中,模块是一个包含了函数、类和变量的文件。模块提供了一种组织代码的方式,使得代码更加可重用和可维护。你可以使用 Python 内置的模块,也可以创建自己的模块。 Python 模块的特点包括: 封装…...

《深入理解计算机系统(CSAPP)》第3章 程序的机器级表示 - 学习笔记
写在前面的话:此系列文章为笔者学习CSAPP时的个人笔记,分享出来与大家学习交流,目录大体与《深入理解计算机系统》书本一致。因是初次预习时写的笔记,在复习回看时发现部分内容存在一些小问题,因时间紧张来不及再次整理…...

【数据结构】第六周
目录 银行排队——队列 公共钥匙盒——队列 等值子串 KMP模式匹配 大整数相乘 最长公共子串 银行排队——队列 【问题描述】 我们大多都有在银行排队的经历,唉,那坑爹的排队啊!现在就让我们来算算我们这些客户平均需要等多久吧。 每天…...
6.4.6拓扑排序
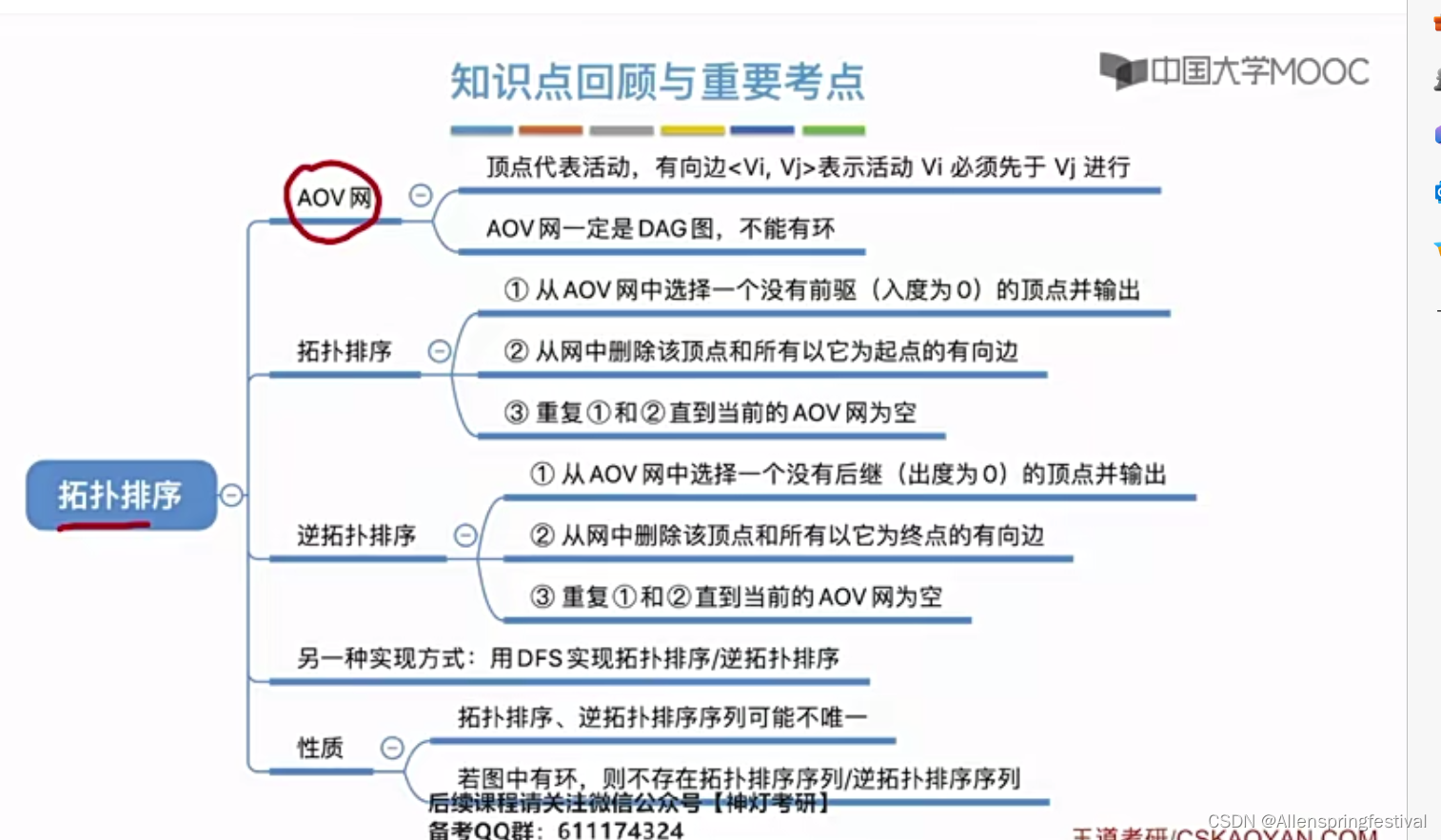
用DAG(有向无环图)表示一个工程。顶点表示活动,有向边<Vi,Vj>表示活动Vi活动必须先与Vj活动进行。 所谓的拓扑排序:找到做事的先后顺序 以上根据拓扑排序的实现: 加入对有回路的图进行拓扑排序&#…...

Ae:常用内置抠像效果
Ae 中的抠像都是基于效果控件来实现的,最终生成动态遮罩来控制画面像素的透明度。 常用的内置抠像效果有:提取、线性颜色键、颜色差值键、内部/外部键等。 黑色或白色背景的抠像 对于白色或黑色背景的素材,可直接尝试图层混合模式。 或者&…...

[ 支付宝支付笔记]
目录 前言: 支付宝支付: 创建AlipayClient对象(注意,这里的appId、私钥、公钥等信息需要根据实际情况进行替换): 构造AlipayTradePagePayRequest对象,设置订单信息等参数: 调用AlipayClient对象的page…...

2023九坤投资暑期实习笔试复盘
5.22号笔试,5.24确认自己笔试挂。想想这也是自己第一次做量化私募基金的笔试,在此复盘一下。情况:北邮本硕。但开始准备暑期准备的比较晚,4月初才开始一边刷题一边投简历,所以手撕算法不太强,但运气和灵感好…...

深度学习的定义和未来发展趋势
深度学习的定义和未来发展趋势 什么是深度学习数学和编程的基础知识深度学习的应用领域深度学习的常见算法和模型训练深度学习模型深度学习的未来 🏘️🏘️个人简介:以山河作礼。 🎖️🎖️:Python领域新星创作者&#…...

如何更改 Linux 文件和目录权限?
在Linux系统中,文件和目录权限是安全性和访问控制的关键组成部分。正确设置文件和目录的权限可以确保只有授权的用户能够读取、写入或执行这些文件和目录。 本文将详细介绍如何在Linux系统中更改文件和目录的权限。 1. 文件和目录权限概述 在Linux系统中ÿ…...
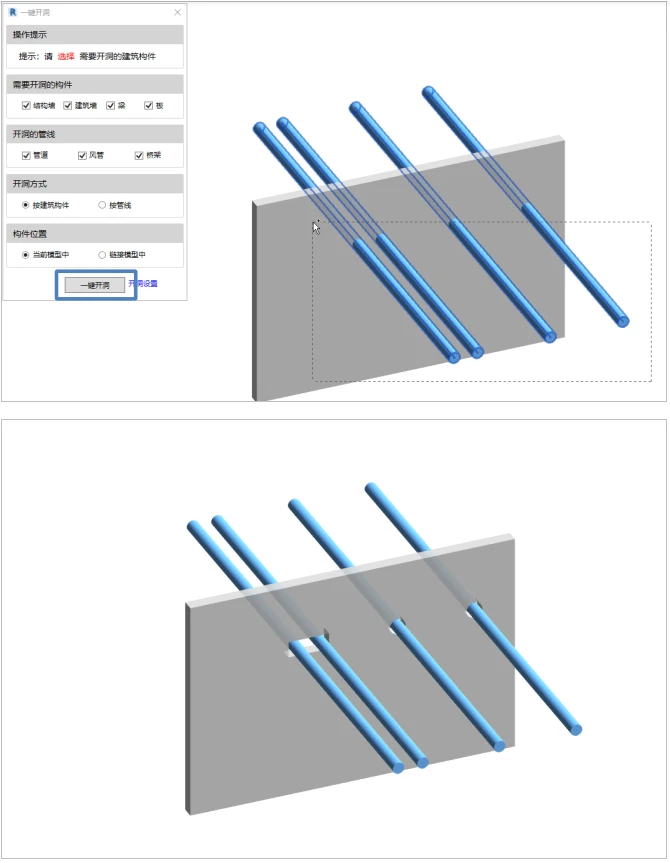
Revit楼板问题:楼板连接处以及楼板开洞,一键开洞
在我们做楼梯时,楼梯与楼板处的连接处理不是那么符合实际,会出现一些问题,如下图,这样的连接会导致楼梯配筋时钢筋外露。 我们来学习如何调节楼板与楼板连接处的高度,选中楼梯,点击“编辑楼梯”在所需要更改…...

【AI领域+餐饮】| 论ChatGPT在餐饮行业的应用展望
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计学专业大二本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后…...

【计算机视觉 | 目标检测】arxiv 计算机视觉关于目标检测的学术速递(5月29日论文合集)
文章目录 一、检测相关(12篇)1.1 Linear Object Detection in Document Images using Multiple Object Tracking1.2 Hybrid Energy Based Model in the Feature Space for Out-of-Distribution Detection1.3 BEV-IO: Enhancing Birds-Eye-View 3D Detection with Instance Occu…...
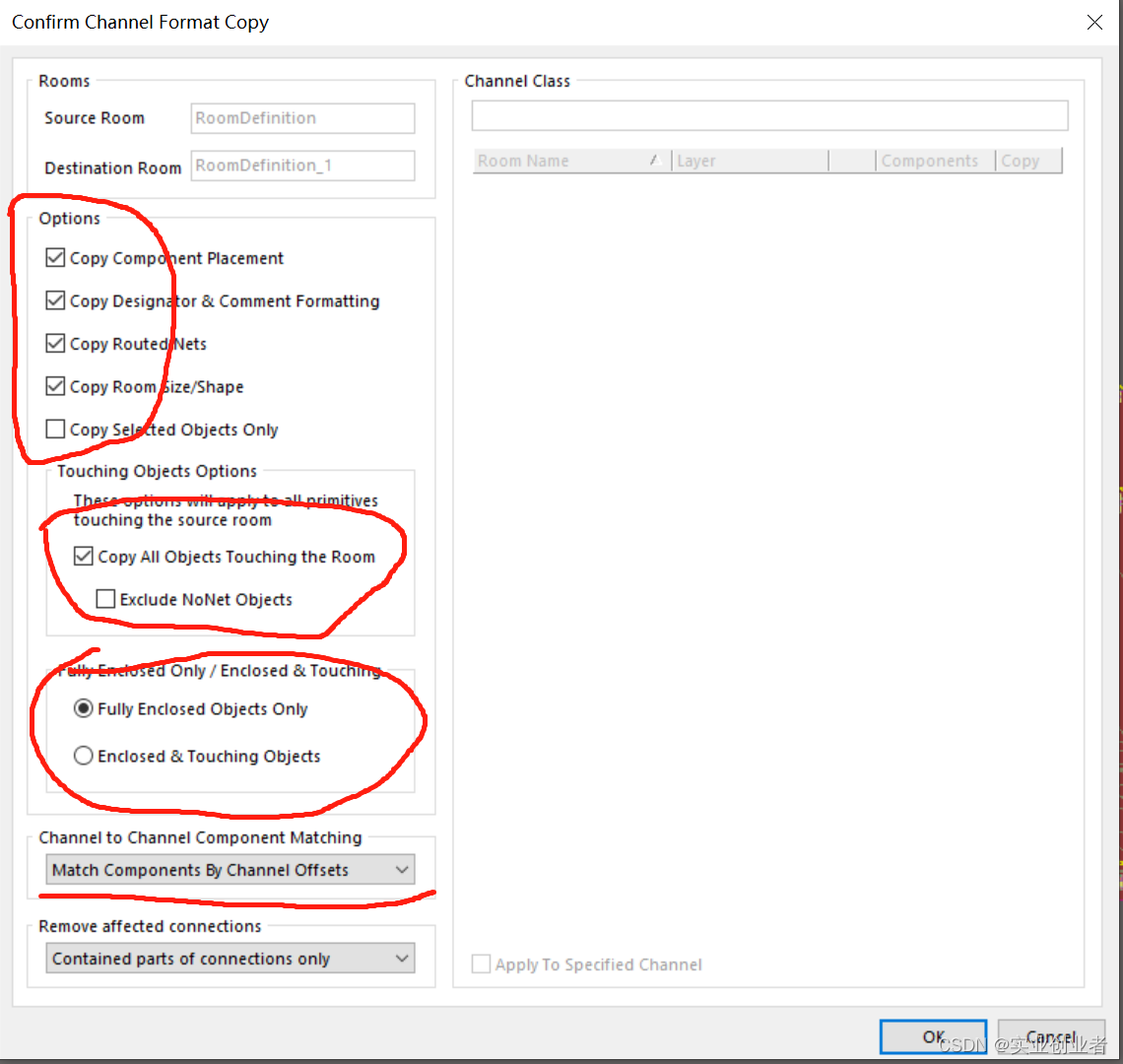
Altium Designer 相同电路多组复制布线
在进行设计开发的时候,总会遇到相同的电路,或者模块,这些电路可以使用相同的布局和走线。我们可以画好其中一部分,然后直接复制,就可以提高效率。下面记录我自己的实际操作过程,有一些地方遇到了问题&#…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...
