【数据结构与算法】图的概述(内含源码)
个人主页:【😊个人主页】
系列专栏:【❤️数据结构与算法】
学习名言:天子重英豪,文章教儿曹。万般皆下品,惟有读书高——《神童诗劝学》

系列文章目录
第一章 ❤️ 学前知识
第二章 ❤️ 单向链表
第三章 ❤️ 递归
…
文章目录
- 系列文章目录
- 前言
- 什么是图?
- 图的分类
- 图按照无方向和有方向分为:无向图和有向图。
- 图按照边分为:稀疏图和稠密图
- 完全图
- 网
- 顶点与边
- 顶点与边的关系
- 图的存储结构
- 邻接列表
- 邻接矩阵
- 图的定义和术语总结
前言
与线性表中的元素是“一对一”的关系和树中的元素是“一对多”的关系不同的是,数据结构中图的元素则是“多对多”的关系。图(Graph)是一种复杂的非线性结构,在图结构中,每个元素都可以有零个或多个前驱,也可以有零个或多个后继,也就是说,元素之间的关系是任意的,今天就让我来带大家了解数据结构中图结构吧。
什么是图?
在计算机科学中,一个图就是一些顶点的集合,这些顶点通过一系列边结对(连接)。顶点用圆圈表示,边就是这些圆圈之间的连线。顶点之间通过边连接。
顶点有时也称为节点或者交点,边有时也称为链接
图有各种形状和大小。边可以有权重(weight),即每一条边会被分配一个正数或者负数值。
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合

图的分类
图按照无方向和有方向分为:无向图和有向图。

不带有箭头指向的图只由顶点和边构成称为无向图,有向图是由顶点和弧(有向边构成)。弧有弧头和弧尾区别。
图按照边分为:稀疏图和稠密图
这是个模糊的概念,同样是相对的概念。
完全图
如果任意两个顶点之间都存在边叫完全图,有向的边叫有向完全图。如果无重复的边或者顶点到自身的边叫简单图。在用数学方式表示时,无向边用()表示,有向边用<>表示。我们目前接触到的图全是简单图。
 没有重复的边或者到自身的边(简单图),右图则有
没有重复的边或者到自身的边(简单图),右图则有
网
 这种边带权值的图叫网
这种边带权值的图叫网
顶点与边
顶点与边的关系
- 顶点的度:顶点关联边的数目。有向图图中有,入度:方向指向顶点的边;出度:方向背向顶点的边。在有向图中顶点的度就是两者之和。
- 路径长度:路径上边或者弧的数目。
图的存储结构
理论上,图就是一堆顶点和边对象而已,那我们又如何用代码来实现它呢?
通常我们有两种选择:邻接列表和邻接矩阵。
邻接列表
邻接表,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。
对于无向图来说,使用邻接表进行存储也会出现数据冗余,表头结点A所指链表中存在一个指向C的表结点的同时,表头结点C所指链表也会存在一个指向A的表结点。

顶点表的各个结点由data(数据域)和Firstedge(指针域)两个域表示,data是数据域,指针域指向边表的第一个结点,即顶点的第一个邻接点。边表结点由adjvex(邻接点域)和next两个域组成。
邻接点域存储某顶点的邻接点在顶点表中坐标,next存储边表中下一个结点指针。
如图中v1顶点与v2、v0互为邻接点,则在v1边表中,adjvex分别为0和2。
有向图也可以用邻接表,出度表叫邻接表,入度表尾逆邻接表。
#include <stdio.h>
#include <stdlib.h>// 邻接表中每个节点的结构体
struct AdjListNode {int dest;struct AdjListNode* next;
};// 邻接表的结构体
struct AdjList {struct AdjListNode *head;
};// 图的结构体
struct Graph {int V;struct AdjList* array;
};// 创建一个新的邻接表节点
struct AdjListNode* newAdjListNode(int dest) {struct AdjListNode* newNode = (struct AdjListNode*)malloc(sizeof(struct AdjListNode));newNode->dest = dest;newNode->next = NULL;return newNode;
}// 创建一个具有V个顶点的新图
struct Graph* createGraph(int V) {struct Graph* graph = (struct Graph*)malloc(sizeof(struct Graph));graph->V = V;// 创建邻接表数组graph->array = (struct AdjList*)malloc(V * sizeof(struct AdjList));// 初始化链表头为空for (int i = 0; i < V; ++i)graph->array[i].head = NULL;return graph;
}// 添加一个边到无向图
void addEdge(struct Graph* graph, int src, int dest) {// 添加一条从src到dest的边struct AdjListNode* newNode = newAdjListNode(dest);newNode->next = graph->array[src].head;graph->array[src].head = newNode;// 添加一条从dest到src的边,因为是无向图newNode = newAdjListNode(src);newNode->next = graph->array[dest].head;graph->array[dest].head = newNode;
}// 打印邻接列表表示的图
void printGraph(struct Graph* graph) {for (int v = 0; v < graph->V; ++v) {struct AdjListNode* pCrawl = graph->array[v].head;printf("\n 邻接列表%d: ", v);while (pCrawl) {printf("-> %d", pCrawl->dest);pCrawl = pCrawl->next;}printf("\n");}
}int main() {// 创建一个具有5个顶点的新图struct Graph* graph = createGraph(5);// 添加边addEdge(graph, 0, 1);addEdge(graph, 0, 2);addEdge(graph, 1, 2);addEdge(graph, 1, 3);addEdge(graph, 2, 3);addEdge(graph, 2, 4);addEdge(graph, 3, 4);// 打印邻接列表表示的图printGraph(graph);return 0;
}
邻接矩阵
邻接矩阵(Adjacency Matrix):是表示顶点之间相邻关系的矩阵。设G=(V,E)是一个图,其中V={v1,v2,…,vn}。G的邻接矩阵是一个具有下列性质的n阶方阵:

- 对无向图而言,邻接矩阵一定是对称的,而且主对角线一定为零(在此仅讨论无向简单图),副对角线不一定为0,有向图则不一定如此。
- 在无向图中,任一顶点i的度为第i列(或第i行)所有非零元素的个数,在有向图中顶点i的出度为第i行所有非零元素的个数,而入度为第i列所有非零元素的个数。
- 用邻接矩阵法表示图共需要n^2个空间,由于无向图的邻接矩阵一定具有对称关系,所以扣除对角线为零外,仅需要存储上三角形或下三角形的数据即可,因此仅需要n(n-1)/2个空间
#include <stdio.h>#define MAX_NODES 100int adj_matrix[MAX_NODES][MAX_NODES];void add_edge(int start, int end) {adj_matrix[start][end] = 1;adj_matrix[end][start] = 1; // 无向图需要将两个方向都标记为已连接
}int main() {// 添加边add_edge(0, 1);add_edge(0, 2);add_edge(1, 2);add_edge(2, 3);// 输出邻接矩阵printf("邻接矩阵:\n");for (int i = 0; i < MAX_NODES; i++) {for (int j = 0; j < MAX_NODES; j++) {printf("%d ", adj_matrix[i][j]);}printf("\n");}return 0;
}
图的定义和术语总结
顶点(Vertex):图中的数据元素通常称为顶点
弧(Arc):若< v,w >∈VR,则< v,w >表示从v到w的一条弧
弧尾(Tail):v为弧尾或初始点(Initial node)
弧头(Head):w为弧头或终端点(Terminal node)
有向图(Digraph):图中每条边都有方向
无向图(Undigraph):图中每条边都没有方向
连通图(Connected Graph):对于图中任意两个顶点v,j∈V,v和j都是连通的,则称G是连通图
连通分量(Connected Compenent):无向图中的极大连通子图
完全图(Completed graph):有1/2*n(n-1)条边的无向图称为完全图
有向完全图:具有n(n-1)条弧的有向图称为有向完全图
稀疏图(Sparse graph):有很少条边或弧(如e < nlogn)的图称为稀疏图
稠密图(Dense graph):有很多条边或弧
权(Weight):有时图的边或弧具有与它相关的数,这种与图的边或弧相关的数叫做权
度(Degree):定点v的度是和v相关联的边的数目,记为TD(V)
入度(InDegree):以顶点v为头的弧的数目称为v的入度,记为ID(v)
出度(Outdegree):以v为尾的弧的数目成为v的出度,记为OD(v)
V: 是顶点的有穷非空集合
VR:是两个顶点之间的关系的集合
n:表示图中顶点数目
e:表示边或弧的数目

相关文章:

【数据结构与算法】图的概述(内含源码)
个人主页:【😊个人主页】 系列专栏:【❤️数据结构与算法】 学习名言:天子重英豪,文章教儿曹。万般皆下品,惟有读书高——《神童诗劝学》 系列文章目录 第一章 ❤️ 学前知识 第二章 ❤️ 单向链表 第三章…...
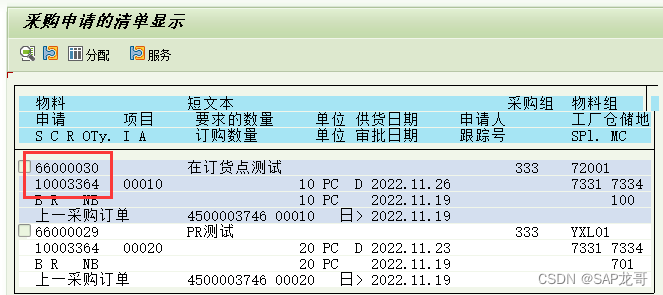
SAP MM 根据采购订单反查采购申请
如何通过采购订单号查询到其前端的采购申请号。 首先从采购申请的相关报表着手,比如ME5A, 发现它是可以满足需求的。 例如:如下的采购订单, 该订单是由采购申请10003364转过来的。 如果想通过这个采购订单找到对应的采购申请,在…...
C语言程序设计题/C语言计算机二级考前押题版
C语言程序设计题/C语言计算机二级考试押题版 与 数位 和 数 有关 求max与min 任意四个数 运算符和表达式版本 #include <stdio.h> int main( ) {int a,b,c,d;int max,min;printf("please input 4 integers:");scanf("%d%d%d%d", &a, &b, …...

Canonical标签在SEO中重要作用
canonical标签是很多搜索引擎都支持的一个标签,它的作用是标记某一网页的唯一url地址。这样做的目的是保证我们的某一网页在搜索引擎中只有一个唯一的地址。 Canonical标签对于一些入行不久的人来说,可能会有些陌生。但这个标签是很多搜索引擎都支持的标…...

【Linux之进程间通信】06.Linux进程通信 - 共享内存
【Linux之进程间通信】 项目代码获取:https://gitee.com/chenshao777/linux-processes.git (麻烦点个免费的Star哦,您的Star就是我的写作动力!) 06.共享内存 共享内存是Linux进程间的通信方式之一 创建共享内存函数…...
oracle安装
服务端安装(公司中不需要,只安装客户端就行) 1、挂载一个Windows系统 双击vmx文件 启动 2、网络配置 添加一个网络 自己电脑看控制面板是否添加虚拟网卡 查看连接的网络,ip地址不能为1,为1就自己修改,…...

CSS样式的三种引入方式及优先级
说明:网页开发有三种技术,分别是html、css和js,分别对应页面的结构、表现和动作。css样式引入,是指把对页面的渲染作用到html上,有以下三种方式:行内式、内嵌式和外联式。 第一种:行内式&#…...

Linux第二天
上传 scp -r 本地文件路劲 用户名目标主机地址:路径 下载:scp -r 用户名目标主机地址:路径 本地目录 ls -A /root //查看root文件下所有的隐藏文件 命令:ls 选项: -l:查看文件属性 -h:文…...
微服务和领域驱动
一、微服务 1.1 什么是微服务 微服务就是一些协同工作的小而自治的服务。 关键词: 小而自治 -- 小 “小”这个概念,一方面体现在微服务的内聚性上。 内聚性也可以称之为单一职责原则:“把因相同原因而变化的东西聚合到一起,…...

Redis如何做到内存高效利用?过期key删除术解析!
大家好,我是小米,一个热衷于分享技术的小伙伴。今天我要和大家探讨一个关于 Redis 的话题:删除过期key。在使用 Redis 进行数据存储和缓存时,我们经常会遇到过期数据的处理问题。接下来,我将为大家介绍为什么要删除过期…...

EFDC模型教程
详情点击链接:EFDC建模方法及在地表水环境评价、水源地划分、排污口论证 一,软件安装 1.1 EFDC安装 1.2 EFDC-Explorer安装 1.3 Delft3D安装 1.4 Google Earth安装二,EFDC模型 2.1 EFDC模型 2.2 EFDC-DSI模型 2.3 EFDC的…...

URLConnection(三)
文章目录 1. 配置连接2. protected URL url3. protected boolean connected4. protected boolean allowUserInteraction5. protected boolean doInput5. protected boolean doOutput6. protected boolean isModifiedSince7. protected boolean useCaches8. 超时 1. 配置连接 U…...
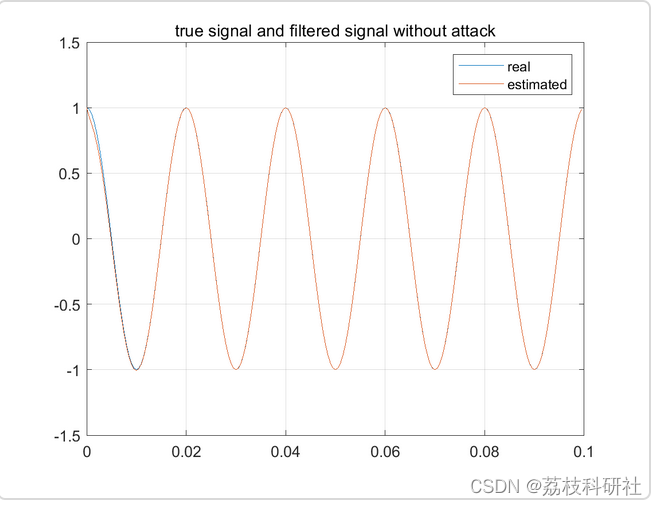
针对KF状态估计的电力系统虚假数据注入攻击研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
)
2023-05-25 LeetCode每日一题(差值数组不同的字符串)
2023-05-25每日一题 一、题目编号 差值数组不同的字符串 二、题目链接 点击跳转到题目位置 三、题目描述 给你一个字符串数组 words ,每一个字符串长度都相同,令所有字符串的长度都为 n 。 每个字符串 words[i] 可以被转化为一个长度为 n - 1 的 …...

MI小米验厂知识点
【MI小米验厂知识点】 小米科技有限责任公司成立于2010年3月3日,是专注于智能硬件和电子产品研发、智能手机、智能电动汽车、互联网电视及智能家居生态链建设的全球化移动互联网企业、创新型科技企业。小米公司创造了用互联网模式开发手机操作系统、发烧友参与开发改…...
损失函数——交叉熵损失(Cross-entropy loss)
交叉熵损失(Cross-entropy loss)是深度学习中常用的一种损失函数,通常用于分类问题。它衡量了模型预测结果与实际结果之间的差距,是优化模型参数的关键指标之一。以下是交叉熵损失的详细介绍。 假设我们有一个分类问题࿰…...

电商ERP接口erp进销存接口
电商API详情接口在ERP中的重要性 电商行业的发展已经改变了人们的消费方式。作为一种连续不断涌现并不断发展的新型销售方式,电商具有开创新市场、大众化消费、商业模式的多样化、效率的提高等优势,对传统零售业产生了极大的冲击。而ERP作为企业资源规划…...

leetcode 922. 按奇偶排序数组 II
题目描述解题思路执行结果 leetcode 922. 按奇偶排序数组 II. 题目描述 按奇偶排序数组 II 给定一个非负整数数组 nums, nums 中一半整数是 奇数 ,一半整数是 偶数 。 对数组进行排序,以便当 nums[i] 为奇数时,i 也是 奇数 &#…...

Unity四叉树地图
当使用Unity构建大规模的游戏地图或场景时,使用四叉树数据结构可以提高性能和效率。四叉树是一种基于分割的数据结构,将空间划分为四个相等的子区域,并以递归方式构建树结构。在游戏开发中,四叉树常用于空间分区、碰撞检测和可视化…...

【unity插件】OpenFracture插件实现物体破裂和切割
插件地址 https://github.com/Mustenaka/OpenFracture 使用注意事项 1.如果要导入自定义网格,则必须在导入设置中将“启用读/写”设置为 true。否则,您将收到错误。 2.网格必须是非相交和封闭的。否则,重新三角测量将失败。 上面描绘的是凳子的线框模型。注意横杆如何与…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...
