leetcode 922. 按奇偶排序数组 II
- 题目描述
- 解题思路
- 执行结果
题目描述
-
按奇偶排序数组 II
给定一个非负整数数组 nums, nums 中一半整数是 奇数 ,一半整数是 偶数 。
对数组进行排序,以便当 nums[i] 为奇数时,i 也是 奇数 ;当 nums[i] 为偶数时, i 也是 偶数 。
你可以返回 任何满足上述条件的数组作为答案 。
示例 1:
输入:nums = [4,2,5,7] 输出:[4,5,2,7] 解释:[4,7,2,5],[2,5,4,7],[2,7,4,5] 也会被接受。 示例 2:
输入:nums = [2,3] 输出:[2,3]
提示:
2 <= nums.length <= 2 * 104 nums.length 是偶数 nums 中一半是偶数 0 <= nums[i] <= 1000
进阶:可以不使用额外空间解决问题吗?
解题思路
法1
进阶:可以不使用额外空间解决问题
方法1:双指针\
-
定义两个指针,一个遍历奇数位一个遍历偶数位
-
分别找出两个不满足奇数对应奇数,偶数对应偶数的条件时,交换两个指针的对应数值,
-
循环遍历数组,输出结果
这个实现的时间复杂度也是 O(n),其中 n 是数组的长度。这种方法只需要遍历一次数组,并且没有使用额外的空间,满足了题目的要求。
-
时间复杂度(O(n)) -
空间复杂度(O(1))
执行结果
法1
我们使用两个指针 evenIndex 和 oddIndex 分别表示奇数索引和偶数索引。我们通过遍历数组并比较当前元素的奇偶性来进行交换操作,直到两个指针超出数组的范围。
如果 nums[evenIndex] 是偶数,则说明它已经在正确的位置上,我们将 evenIndex 增加 2。
如果 nums[oddIndex] 是奇数,则说明它已经在正确的位置上,我们将 oddIndex 增加 2。
如果 nums[evenIndex] 是奇数,且 nums[oddIndex] 是偶数,说明它们不满足奇数对应奇数、偶数对应偶数的条件,我们将它们交换,并将 evenIndex 和 oddIndex 分别增加 2。
最后,返回经过排序的数组 nums。
func sortArrayByParityII(nums []int) []int {
n := len(nums)
evenIndex := 0
oddIndex := 1
for evenIndex < n && oddIndex < n {
if nums[evenIndex]%2 == 0 {
evenIndex += 2
} else if nums[oddIndex]%2 != 0 {
oddIndex += 2
} else {
nums[evenIndex], nums[oddIndex] = nums[oddIndex], nums[evenIndex]
evenIndex += 2
oddIndex += 2
}
}
return nums
}
执行结果:
执行用时: 12 ms , 在所有 Go 提交中击败了 98.74% 的用户 内存消耗: 6.2 MB , 在所有 Go 提交中击败了 91.20% 的用户 通过测试用例: 61 / 61 炫耀一下:
本文由 mdnice 多平台发布
相关文章:

leetcode 922. 按奇偶排序数组 II
题目描述解题思路执行结果 leetcode 922. 按奇偶排序数组 II. 题目描述 按奇偶排序数组 II 给定一个非负整数数组 nums, nums 中一半整数是 奇数 ,一半整数是 偶数 。 对数组进行排序,以便当 nums[i] 为奇数时,i 也是 奇数 &#…...

Unity四叉树地图
当使用Unity构建大规模的游戏地图或场景时,使用四叉树数据结构可以提高性能和效率。四叉树是一种基于分割的数据结构,将空间划分为四个相等的子区域,并以递归方式构建树结构。在游戏开发中,四叉树常用于空间分区、碰撞检测和可视化…...

【unity插件】OpenFracture插件实现物体破裂和切割
插件地址 https://github.com/Mustenaka/OpenFracture 使用注意事项 1.如果要导入自定义网格,则必须在导入设置中将“启用读/写”设置为 true。否则,您将收到错误。 2.网格必须是非相交和封闭的。否则,重新三角测量将失败。 上面描绘的是凳子的线框模型。注意横杆如何与…...

Spring Security实现登录
前言 Spring Security是Spring框架下的一个用于身份验证和授权的框架,它可以帮忙管理web应用中的用户认证、授权以及安全性问题。本文将介绍如何使用Spring Security实现用户登录功能,本文主要包括以下内容: 环境准备Spring Security核心概…...

小狐狸ChatGPT付费创作系统1.9.7独立版 + H5端 + 小程序前端增加AI绘画+GPT4接口
小狐狸ChatGPT 1.9.7独立版经播播资源测试了版本比较,本版核心增加了GPT4.0接口功能,小程序端内置了AI绘画功能。体验下来问答速度感觉体验更好。小程序端有更新请对应开发工具更新上传,本版无开源端。播播资源提供的安装教程详见下方&#x…...
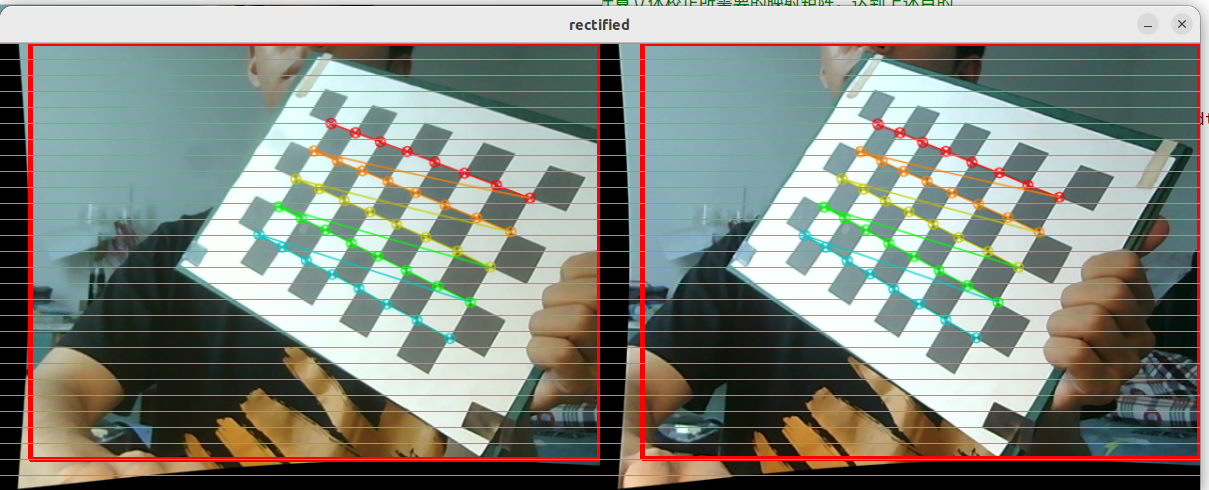
双目测距联合YOLOv8 项目总结
代码贴:双目测距--5 双目相机 联合 YOLOv8_爱钓鱼的歪猴的博客-CSDN博客 0、图片筛选 可以用matlab,对双目图像做个一个筛选,也就是做双目标定。 熟悉matlab的小伙伴完全可以用matlab做双目标定,我是没咋接触过不知道怎么导出标定结果&#…...
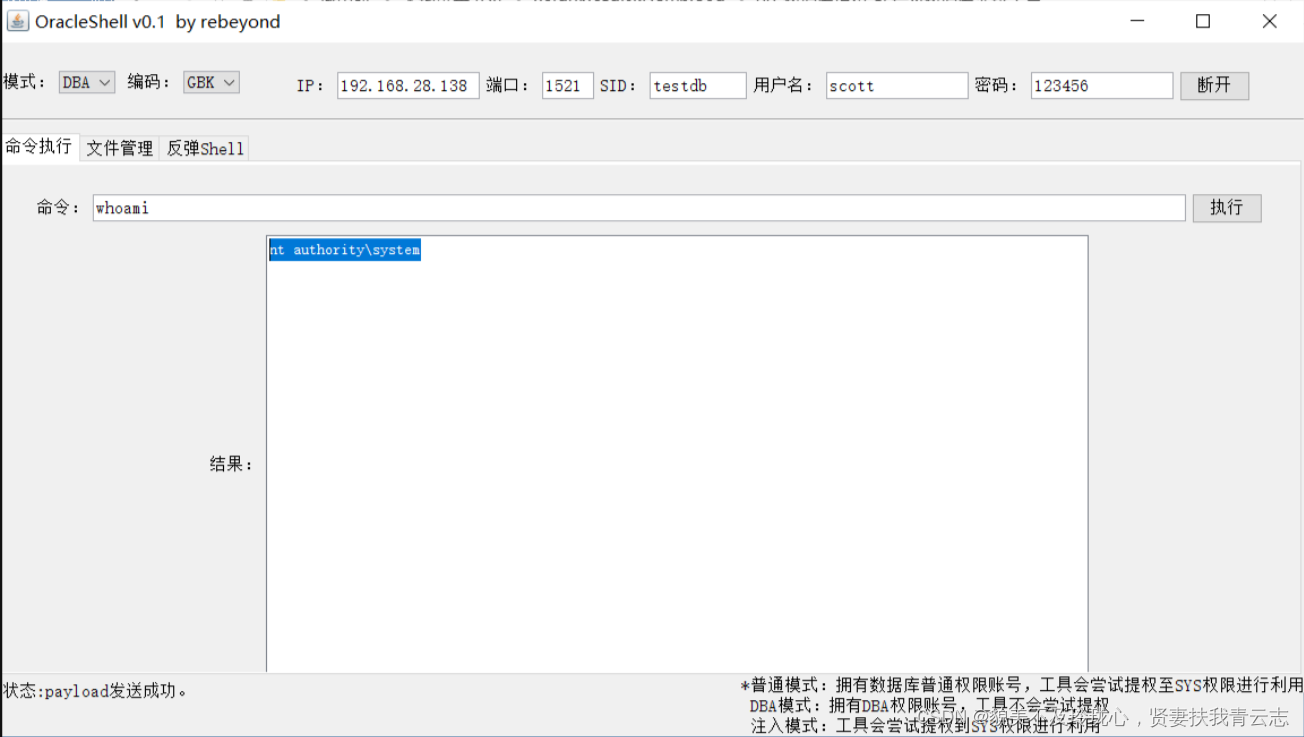
Windows提权:利用MSSQL数据库,Oracle数据库
目录 MSSQL提权:使用xp_cmdshell进行提权 MSSQL:使用sp_OACreate进行提权 MSSQL:使用沙盒提权 Oracle提权:工具一把梭哈 总结 MSSQL在Windows server类的操作系统上,默认具有system权限。 MSSQL提权:使…...

linux常见的二十多个指令
目录 一、指令的概念 二、28个常见的指令 ⭐2.1 ls指令 ⭐2.2 pwd指令 ⭐2.3 cd指令 ⭐2.4tree指令 ⭐2.5 mkdir指令 ⭐2.6 touch指令 ⭐2.7 rmdir指令 ⭐2.8 rm指令 ⭐2.9 clear指令 ⭐2.10 man指令 ⭐2.11 cp指令 ⭐2.12 mv指令 ⭐2.13 cat指令(适…...
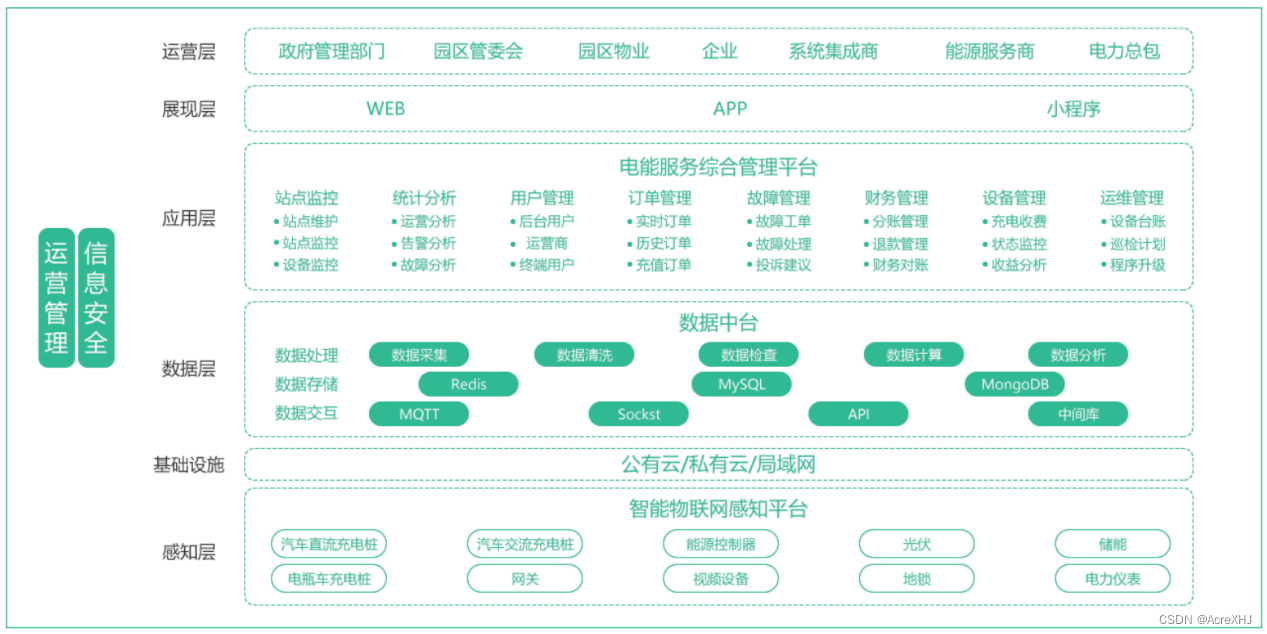
内蒙古自治区住房和城乡建设分析及解决方案
安科瑞 徐浩竣 江苏安科瑞电器制造有限公司 zx acrelxhj 摘 要:为深入贯彻落实《国务院办公厅关于印发新能源汽车产业发展规划(2021—2035年)的通知》(国办发 ﹝2020﹞39号)、《国家发展改革委等部门关于进一步提升…...
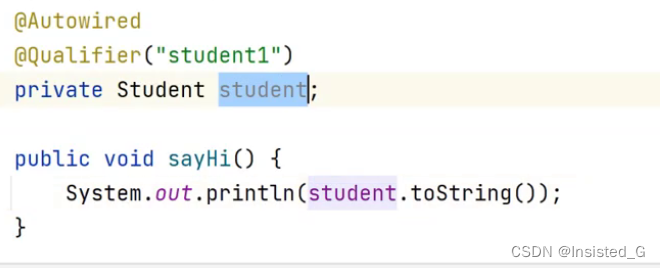
JavaEE进阶5/25(属性注入)
目录 1.更简单的存取Spring对象 2.获取Bean对象(对象装配)DI 3. Resource注入 4.Resource注入和Autowired注入的区别 1.更简单的存取Spring对象 2.获取Bean对象(对象装配)DI 对象装配(对象注入)有三种方…...
)
【Java学习记录-4】相关名词和概念记录(持续更新)
目录 1 注解2 包3 权限修饰符4 状态修饰符1. final2. static 5. 多态6.抽象类7.接口 1 注解 Override是一个注解,可以帮助我们检查重写方法的方法声明的正确性 注意: 私有方法不能被重写(父类私有成员子类是不能继承的)子类方法…...

《程序员面试金典(第6版)》面试题 16.25. LRU 缓存(自定义双向链表,list库函数,哈希映射)
题目描述 设计和构建一个“最近最少使用”缓存,该缓存会删除最近最少使用的项目。缓存应该从键映射到值(允许你插入和检索特定键对应的值),并在初始化时指定最大容量。当缓存被填满时,它应该删除最近最少使用的项目。 题目传送门:…...
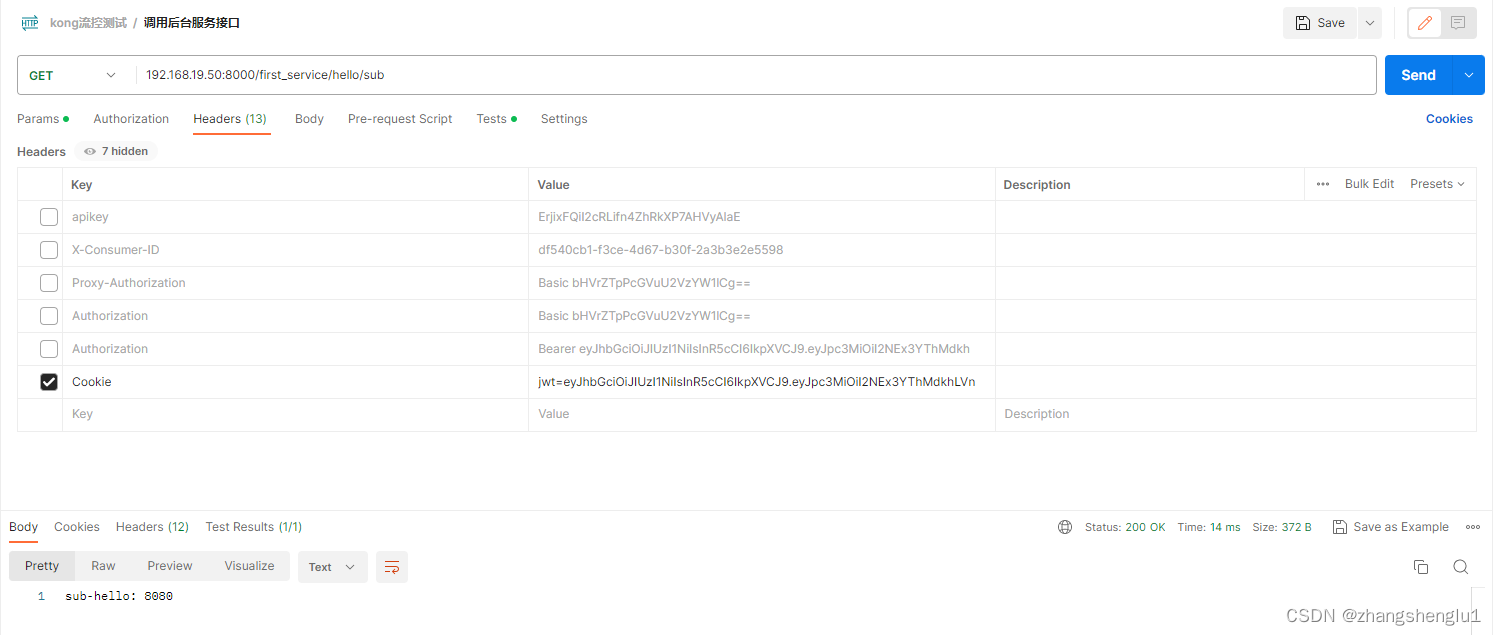
kong网关启用jwt认证插件
认证流程: 1、创建一个用户 2、生成jwt的所需要的key和密钥 3、在https://jwt.io/的生成jwt token 4、启用jwt插件 5、发送请求的时候携带jwt的token信息 官方指导:https://docs.konghq.com/hub/kong-inc/jwt/configuration/examples/ 一、创建一个新的…...
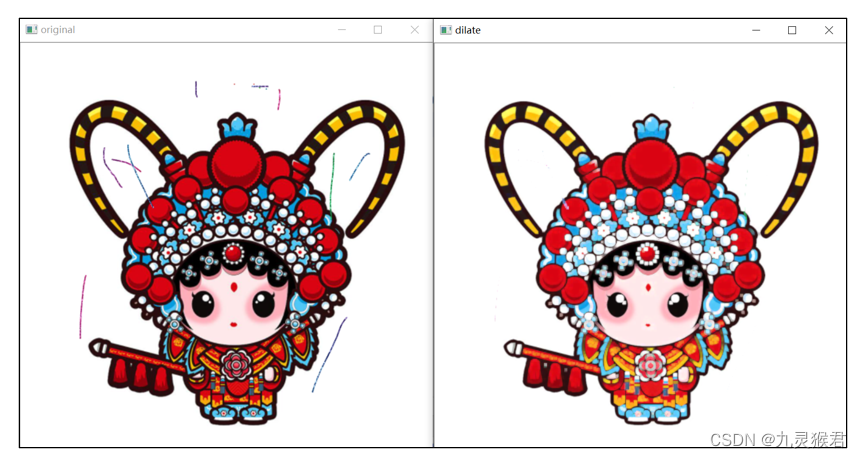
day12 - 图像修复
在图像处理的过程中,经常会遇到图像存在多余的线条或者噪声的情况,对于这种情况我们会先对图像进行预处理,去除掉对图形内容有影响的噪声,在进行后续的处理。 本节实验我们介绍使用图像膨胀来处理图形的多余线条,进行…...

1720_Linux学习中的问题处理
全部学习汇总:GreyZhang/little_bits_of_linux: My notes on the trip of learning linux. (github.com) 这个有点学习的方法论的意思,画个滋味导图顺便整理一下。 遇到问题的时候,解决的方法大致有3中,而针对学习的建议有一部分是…...

七人拼团系统开发模式详解
七人拼团是最近兴起的一个模式,它通过更人性化的奖励机制,将产品利润最大化让利给参与拼团的用户,达到促进用户主动积极裂变和团队平台引流提升销量的效果,下面就来详细说一下这个模式。 七人拼团最大的特点,就是结合了…...

CPU性能优化:分支预测
条件跳转引起的控制冒险虽然也可以通过在流水线中插入空泡来避免,但是当流水线很深时,需要插入更多的空泡。一个20级的流水线为例,如果一条指令需要上一条指令的执行结束才能执行,则需要在这两条指令之间插入19个空泡,…...
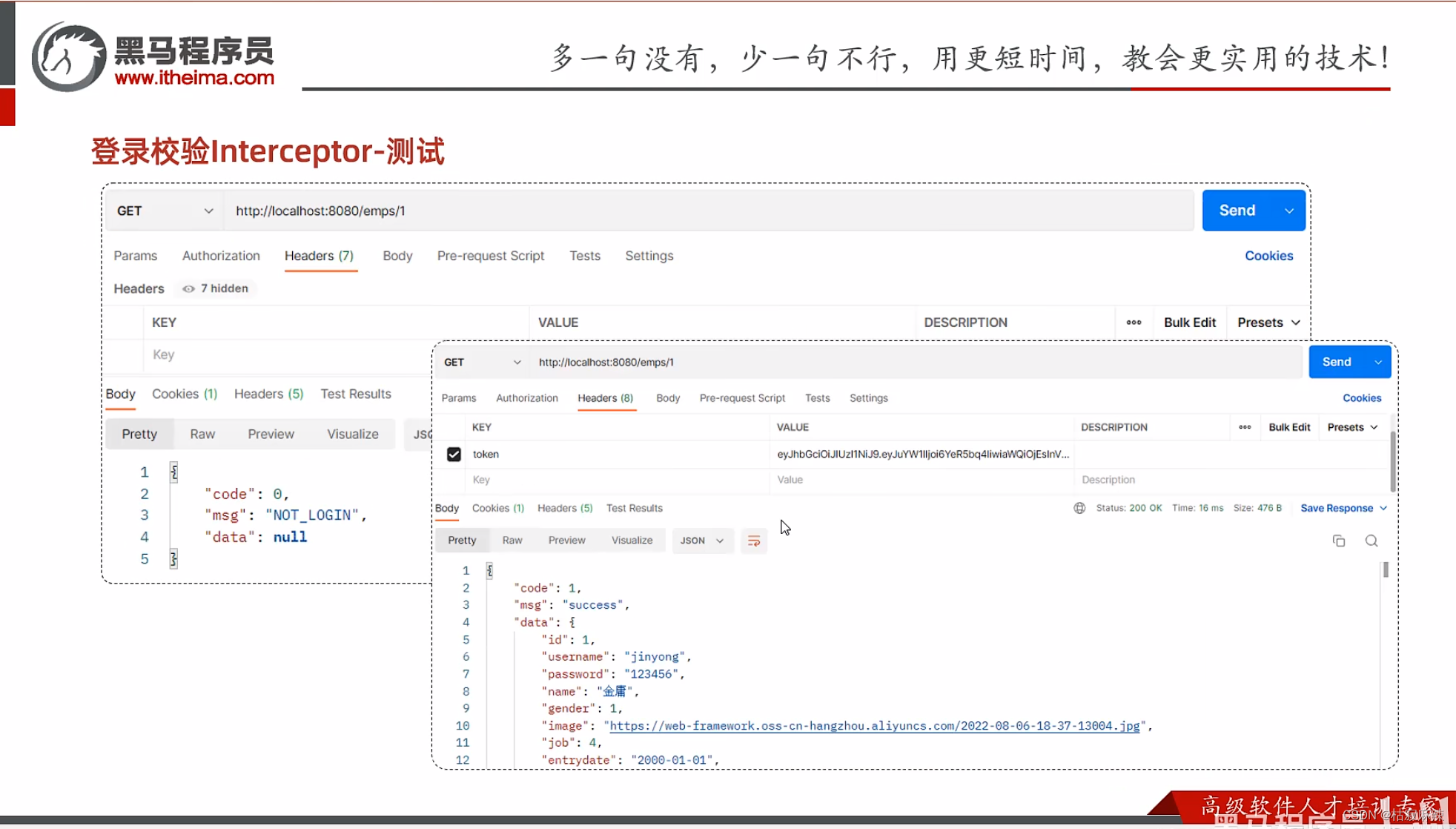
过滤器Filter,拦截器Interceptor
过滤器Filter 快速入门 详情 登录校验-Filter package com.itheima.filter;import com.alibaba.fastjson.JSONObject; import com.itheima.pojo.Result; import com.itheima.utils.JwtUtils; import lombok.extern.slf4j.Slf4j; import org.springframework.util.StringUtils…...

kafka整理
kafka整理 一、kafka概述 kafka是apache旗下一款开源的顶级的消息队列的系统, 最早是来源于领英, 后期将其贡献给apache, 采用语言是scala.基于zookeeper, 启动kafka集群需要先启动zookeeper集群, 同时在zookeeper记录kafka相关的元数据 kafka本质上就是消息队列的中间件产品…...
为什么有些情况下需要重写equals()和hashCode()方法?
目录 方法作用实战案例 方法作用 equals():判断对象是否相等,比如判断是否能放入Set集合中 情况1:没有重写equals()方法:由于所有类的默认基类都是Object类,所以默认使用Object类的equals()方法,那就是对象…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...

Yolo11改进策略:Block改进|FCM,特征互补映射模块|AAAI 2025|即插即用
1 论文信息 FBRT-YOLO(Faster and Better for Real-Time Aerial Image Detection)是由北京理工大学团队提出的专用于航拍图像实时目标检测的创新框架,发表于AAAI 2025。论文针对航拍场景中小目标检测的核心难题展开研究,重点解决…...
[KCTF]CORE CrackMe v2.0
这个Reverse比较古老,已经有20多年了,但难度确实不小。 先查壳 upx压缩壳,0.72,废弃版本,工具无法解压。 反正不用IDA进行调试,直接x32dbg中,dump内存,保存后拖入IDA。 这里说一下…...

创客匠人:如何通过创始人IP打造实现知识变现与IP变现的长效增长?
在流量红利逐渐消退的当下,创始人IP的价值愈发凸显。它不仅能够帮助中小企业及个人创业者突破竞争壁垒,还能成为企业品牌影响力的核心资产。然而,市场上IP孵化机构鱼龙混杂,如何选择一家真正具备长期价值的合作伙伴?创…...

C++ 使用 ffmpeg 解码 rtsp 流并获取每帧的YUV数据
一、简介 FFmpeg 是一个开源的多媒体处理框架,非常适用于处理音视频的录制、转换、流化和播放。 二、代码 示例代码使用工作线程读取rtsp视频流,自动重连,支持手动退出,解码并将二进制文件保存下来。 注意: 代…...
