2023-05-25 LeetCode每日一题(差值数组不同的字符串)
2023-05-25每日一题
一、题目编号
- 差值数组不同的字符串
二、题目链接
点击跳转到题目位置
三、题目描述
给你一个字符串数组 words ,每一个字符串长度都相同,令所有字符串的长度都为 n 。
每个字符串 words[i] 可以被转化为一个长度为 n - 1 的 差值整数数组 difference[i] ,其中对于 0 <= j <= n - 2 有 difference[i][j] = words[i][j+1] - words[i][j] 。注意两个字母的差值定义为它们在字母表中 位置 之差,也就是说 ‘a’ 的位置是 0 ,‘b’ 的位置是 1 ,‘z’ 的位置是 25 。
- 比方说,字符串 “acb” 的差值整数数组是 [2 - 0, 1 - 2] = [2, -1] 。
words 中所有字符串 除了一个字符串以外 ,其他字符串的差值整数数组都相同。你需要找到那个不同的字符串。
请你返回 words中 差值整数数组 不同的字符串。
四、解题代码
class Solution {map<vector<int>, int> hash;
public:string oddString(vector<string>& words) {string s;int n = words.size();vector<vector<int>> res;res.resize(n+1);for(int i = 0; i < n; ++i){for(int j = 0; j < words[i].size() - 1; ++j){res[i].push_back(words[i][j+1] - words[i][j]);}hash[res[i]]++;}for(int i = 0; i < n; ++i){if(hash[res[i]] == 1){return words[i];}}return " ";}
};
五、解题思路
(1) 在题目中有描述除了一个字符串以外,找到那个不同的字符串这样的字样,我们考虑到的是用哈希表来进行统计。
(2) 下面所要做的就是如何先初始化这个哈希表,用map<vector , int> hash来表示前者表示差值整数数组,后者表示个数。
(3) 遍历字符串数组,遍历每一个字符串,求出每一个字符串的差值整数数组,然后在哈希表中自增计数。(用一个res数组保存每一个下标的差值整数数组)
(4) 最后遍历res数组,如果对应的下标的差值整数数组在哈希表中的个数为1个,那么就返回该下标对应的字符串即可。
相关文章:
)
2023-05-25 LeetCode每日一题(差值数组不同的字符串)
2023-05-25每日一题 一、题目编号 差值数组不同的字符串 二、题目链接 点击跳转到题目位置 三、题目描述 给你一个字符串数组 words ,每一个字符串长度都相同,令所有字符串的长度都为 n 。 每个字符串 words[i] 可以被转化为一个长度为 n - 1 的 …...

MI小米验厂知识点
【MI小米验厂知识点】 小米科技有限责任公司成立于2010年3月3日,是专注于智能硬件和电子产品研发、智能手机、智能电动汽车、互联网电视及智能家居生态链建设的全球化移动互联网企业、创新型科技企业。小米公司创造了用互联网模式开发手机操作系统、发烧友参与开发改…...
损失函数——交叉熵损失(Cross-entropy loss)
交叉熵损失(Cross-entropy loss)是深度学习中常用的一种损失函数,通常用于分类问题。它衡量了模型预测结果与实际结果之间的差距,是优化模型参数的关键指标之一。以下是交叉熵损失的详细介绍。 假设我们有一个分类问题࿰…...

电商ERP接口erp进销存接口
电商API详情接口在ERP中的重要性 电商行业的发展已经改变了人们的消费方式。作为一种连续不断涌现并不断发展的新型销售方式,电商具有开创新市场、大众化消费、商业模式的多样化、效率的提高等优势,对传统零售业产生了极大的冲击。而ERP作为企业资源规划…...

leetcode 922. 按奇偶排序数组 II
题目描述解题思路执行结果 leetcode 922. 按奇偶排序数组 II. 题目描述 按奇偶排序数组 II 给定一个非负整数数组 nums, nums 中一半整数是 奇数 ,一半整数是 偶数 。 对数组进行排序,以便当 nums[i] 为奇数时,i 也是 奇数 &#…...

Unity四叉树地图
当使用Unity构建大规模的游戏地图或场景时,使用四叉树数据结构可以提高性能和效率。四叉树是一种基于分割的数据结构,将空间划分为四个相等的子区域,并以递归方式构建树结构。在游戏开发中,四叉树常用于空间分区、碰撞检测和可视化…...

【unity插件】OpenFracture插件实现物体破裂和切割
插件地址 https://github.com/Mustenaka/OpenFracture 使用注意事项 1.如果要导入自定义网格,则必须在导入设置中将“启用读/写”设置为 true。否则,您将收到错误。 2.网格必须是非相交和封闭的。否则,重新三角测量将失败。 上面描绘的是凳子的线框模型。注意横杆如何与…...

Spring Security实现登录
前言 Spring Security是Spring框架下的一个用于身份验证和授权的框架,它可以帮忙管理web应用中的用户认证、授权以及安全性问题。本文将介绍如何使用Spring Security实现用户登录功能,本文主要包括以下内容: 环境准备Spring Security核心概…...

小狐狸ChatGPT付费创作系统1.9.7独立版 + H5端 + 小程序前端增加AI绘画+GPT4接口
小狐狸ChatGPT 1.9.7独立版经播播资源测试了版本比较,本版核心增加了GPT4.0接口功能,小程序端内置了AI绘画功能。体验下来问答速度感觉体验更好。小程序端有更新请对应开发工具更新上传,本版无开源端。播播资源提供的安装教程详见下方&#x…...
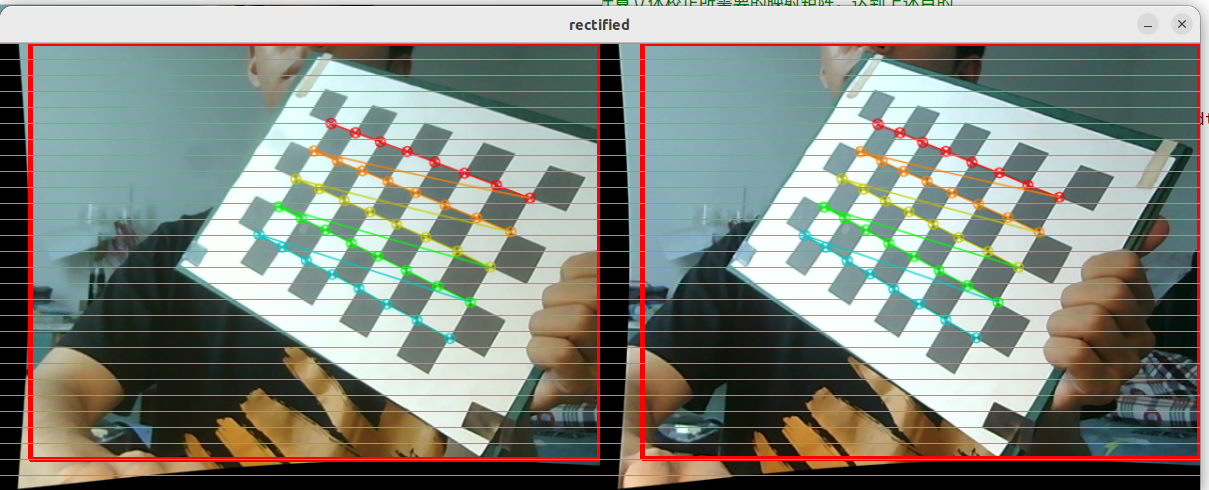
双目测距联合YOLOv8 项目总结
代码贴:双目测距--5 双目相机 联合 YOLOv8_爱钓鱼的歪猴的博客-CSDN博客 0、图片筛选 可以用matlab,对双目图像做个一个筛选,也就是做双目标定。 熟悉matlab的小伙伴完全可以用matlab做双目标定,我是没咋接触过不知道怎么导出标定结果&#…...
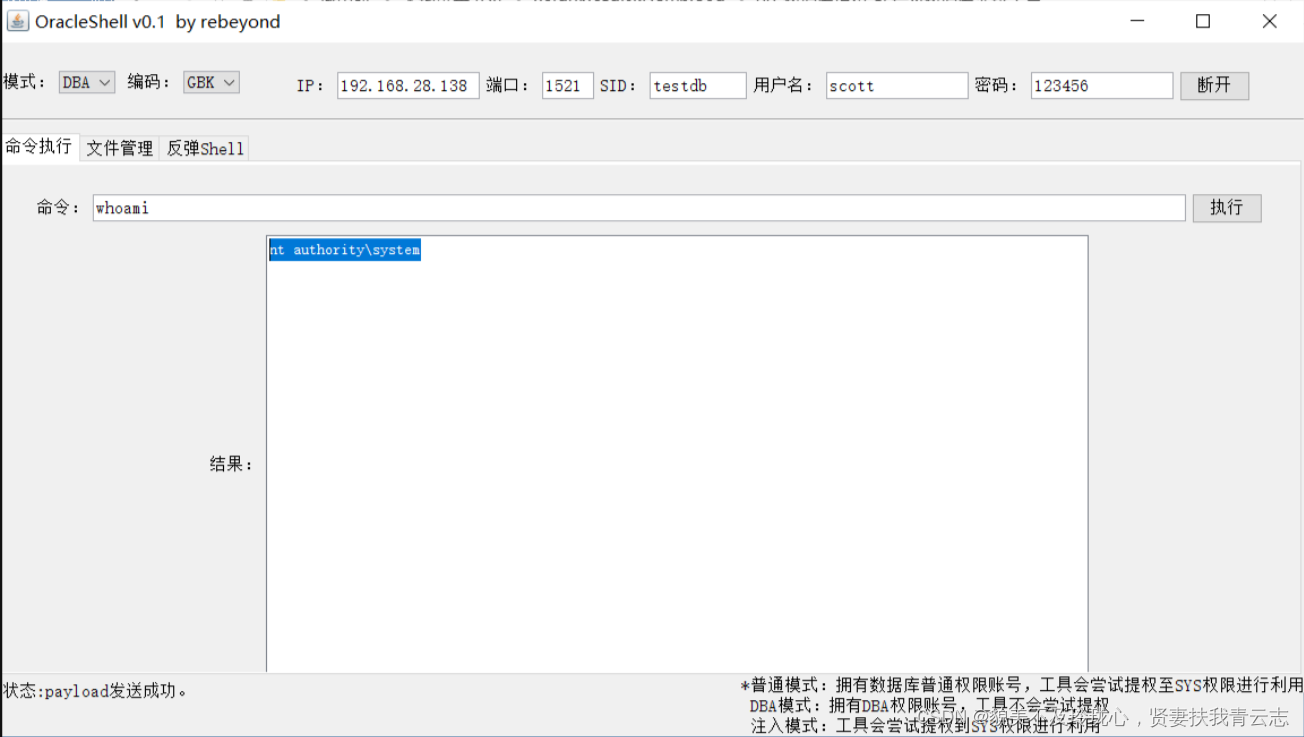
Windows提权:利用MSSQL数据库,Oracle数据库
目录 MSSQL提权:使用xp_cmdshell进行提权 MSSQL:使用sp_OACreate进行提权 MSSQL:使用沙盒提权 Oracle提权:工具一把梭哈 总结 MSSQL在Windows server类的操作系统上,默认具有system权限。 MSSQL提权:使…...

linux常见的二十多个指令
目录 一、指令的概念 二、28个常见的指令 ⭐2.1 ls指令 ⭐2.2 pwd指令 ⭐2.3 cd指令 ⭐2.4tree指令 ⭐2.5 mkdir指令 ⭐2.6 touch指令 ⭐2.7 rmdir指令 ⭐2.8 rm指令 ⭐2.9 clear指令 ⭐2.10 man指令 ⭐2.11 cp指令 ⭐2.12 mv指令 ⭐2.13 cat指令(适…...
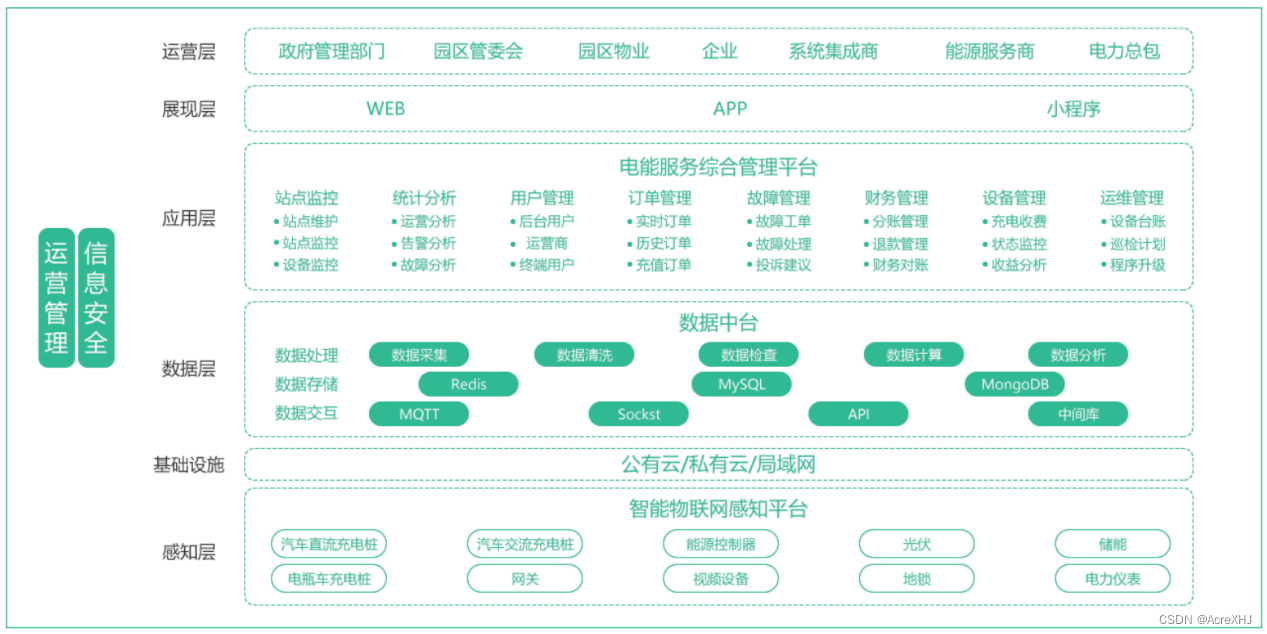
内蒙古自治区住房和城乡建设分析及解决方案
安科瑞 徐浩竣 江苏安科瑞电器制造有限公司 zx acrelxhj 摘 要:为深入贯彻落实《国务院办公厅关于印发新能源汽车产业发展规划(2021—2035年)的通知》(国办发 ﹝2020﹞39号)、《国家发展改革委等部门关于进一步提升…...
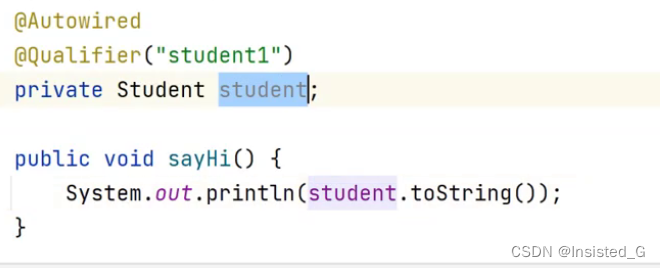
JavaEE进阶5/25(属性注入)
目录 1.更简单的存取Spring对象 2.获取Bean对象(对象装配)DI 3. Resource注入 4.Resource注入和Autowired注入的区别 1.更简单的存取Spring对象 2.获取Bean对象(对象装配)DI 对象装配(对象注入)有三种方…...
)
【Java学习记录-4】相关名词和概念记录(持续更新)
目录 1 注解2 包3 权限修饰符4 状态修饰符1. final2. static 5. 多态6.抽象类7.接口 1 注解 Override是一个注解,可以帮助我们检查重写方法的方法声明的正确性 注意: 私有方法不能被重写(父类私有成员子类是不能继承的)子类方法…...

《程序员面试金典(第6版)》面试题 16.25. LRU 缓存(自定义双向链表,list库函数,哈希映射)
题目描述 设计和构建一个“最近最少使用”缓存,该缓存会删除最近最少使用的项目。缓存应该从键映射到值(允许你插入和检索特定键对应的值),并在初始化时指定最大容量。当缓存被填满时,它应该删除最近最少使用的项目。 题目传送门:…...
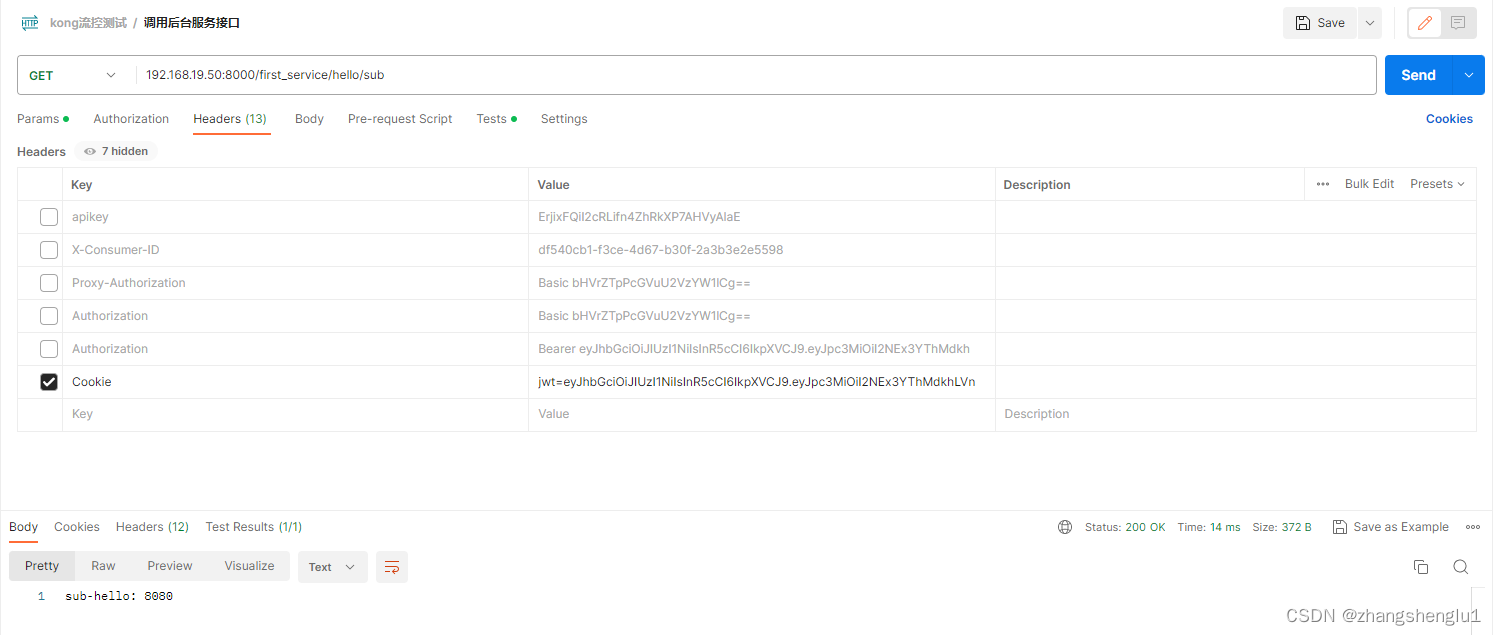
kong网关启用jwt认证插件
认证流程: 1、创建一个用户 2、生成jwt的所需要的key和密钥 3、在https://jwt.io/的生成jwt token 4、启用jwt插件 5、发送请求的时候携带jwt的token信息 官方指导:https://docs.konghq.com/hub/kong-inc/jwt/configuration/examples/ 一、创建一个新的…...
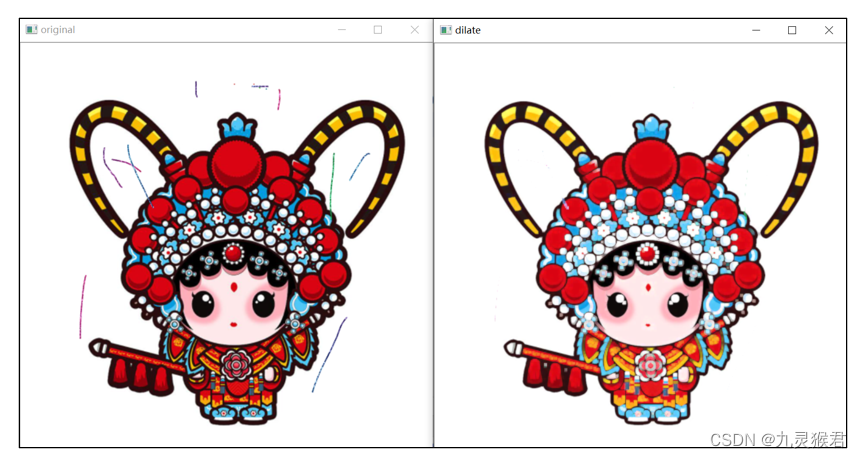
day12 - 图像修复
在图像处理的过程中,经常会遇到图像存在多余的线条或者噪声的情况,对于这种情况我们会先对图像进行预处理,去除掉对图形内容有影响的噪声,在进行后续的处理。 本节实验我们介绍使用图像膨胀来处理图形的多余线条,进行…...

1720_Linux学习中的问题处理
全部学习汇总:GreyZhang/little_bits_of_linux: My notes on the trip of learning linux. (github.com) 这个有点学习的方法论的意思,画个滋味导图顺便整理一下。 遇到问题的时候,解决的方法大致有3中,而针对学习的建议有一部分是…...

七人拼团系统开发模式详解
七人拼团是最近兴起的一个模式,它通过更人性化的奖励机制,将产品利润最大化让利给参与拼团的用户,达到促进用户主动积极裂变和团队平台引流提升销量的效果,下面就来详细说一下这个模式。 七人拼团最大的特点,就是结合了…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
[KCTF]CORE CrackMe v2.0
这个Reverse比较古老,已经有20多年了,但难度确实不小。 先查壳 upx压缩壳,0.72,废弃版本,工具无法解压。 反正不用IDA进行调试,直接x32dbg中,dump内存,保存后拖入IDA。 这里说一下…...
