ObjectARX如何判断点和多段线的关系
目录
- 1 基本思路
- 2 相关知识点
- 2.1 ECS坐标系概述
- 2.2 其他点坐标转换接口
- 2.3 如何获取多段线的顶点ECS坐标
- 3 实现例程
- 3.1 接口实现
- 3.2 测试代码
- 4 实现效果
在CAD的二次开发中,点和多段线的关系是一个非常重要且常见的问题,本文实现例程以张帆所著《ObjectARX 开发基础与实例教程》为基础,并完善和修复了部分问题。
1 基本思路
点和多段线的关系判断算法有两个思路:叉乘判断法(适用于凸多边形)和射线法,本文以射线法进行代码实现。其基本思路为:
- 如果点在多段线上,返回该结果。
- 从给定点出发,沿某个方向做一条射线,计算射线与多边形交点的数量。如果交点数量为奇数,那么点在图形内部;如果交点数量为偶数,那么点在图形外部。
- 在第2条的基础上,排除交点在多段线的顶点上的情况;若出现该情况,需要旋转射线重新判断。
2 相关知识点
2.1 ECS坐标系概述
在该例程中,有一个关键点是理解ECS(或者OCS)坐标系统。
ECS是实体(对象)坐标系,其原点是WCS的原点,X和Y轴所在平面的法向量是实体的法向量。ECS的 X 轴和Y轴的方向由任意轴算法确定,也就是X、Y轴的方向是由法向量与 WCS 的关系来确定的。因此,ECS的X 轴和Y轴是唯一且仅由法向量决定的。另外,ECS的Z坐标是指xy平面距离WCS原点的距离(有正负)。
在ObjectARX有一个暴露的接口可以完成WCS→ECS的转换
bool acdbWcs2Ecs(ads_point p,ads_point q,ads_point norm,bool vec);
上述接口的实现应该是下列办法
//将WCS转为一个平面实体的ECS坐标
int Wcs2Ecs(const AcGeVector3d vtNorm, const AcGePoint3d ptWcs, BOOL bDisp, AcGePoint3d& ptEcs)
{struct resbuf fromrb, torb;fromrb.restype = RTSHORT;fromrb.resval.rint = 0; // WCS torb.restype = RT3DPOINT;ads_point_set(asDblArray(vtNorm), torb.resval.rpoint);return acedTrans(asDblArray(ptWcs), &fromrb, &torb, bDisp, asDblArray(ptEcs));
}
理解了上述知识点,我们之后在判断射线和多段线关系的时候,就可以把射线转为多段线的ECS坐标,然后在多段线所在的ECS平面上,比较射线和多段线的每一条线段的相交关系。从而可以优化算法。
2.2 其他点坐标转换接口
- 点或向量坐标变换
| 函数名 | 作用 |
|---|---|
| acdbUcs2Ecs | UCS→ECS |
| acdbEcs2Ucs | ECS→UCS |
| acdbUcs2Wcs | UCS→WCS |
| acdbWcs2Ucs | WCS→UCS |
| acdbEcs2Wcs | ECS→WCS |
| acdbWcs2Ecs | WCS→ECS |
- AcGePoint3d和ads_point互转
| 函数名 | 作用 |
|---|---|
| AcGePoint3d (AcGePoint2d ) → ads_point | asDblArray |
| ads_point → AcGePoint3d (AcGePoint2d ) | aspnt3d 或 asPnt2d |
2.3 如何获取多段线的顶点ECS坐标
多段线获取顶点坐标有两种重载形式:
Acad::ErrorStatus getPointAt(unsigned int, AcGePoint3d& pt
) const;
Acad::ErrorStatus getPointAt(unsigned int index, AcGePoint2d& pt
) const;
其中第一种获取的是顶点的WCS坐标,第二种获取的是顶点的ECS 2D坐标。这个区别一定要看仔细。
3 实现例程
3.1 接口实现
该例程在张帆所著方法的基础上,增加了对UCS坐标系的支持。在此,再次向原书作者表达敬意。
#include "dbxutil.h"
#define POINT_POLY_INSIDE 1
#define POINT_POLY_OUTSIDE 0
#define POINT_POLY_ONEDGE 2// 在数组中查找某个点,返回点在数组中的索引,未找到则返回-1
int FindPoint(const AcGePoint2dArray &points, const AcGePoint2d &point, double tol /*= 1.0E-7*/)
{TADSGePoint3d pt1;TADSGePoint3d pt2(point);for (int i = 0; i < points.length(); i++){pt1 = points[i];if (IsEqual(pt1, pt2, tol)){return i;}}return -1;
}//-----------------------------------------------------------------------------+
//=Description: 几何类射线和多段线的交点
//=Parameter: pPoly[in] 多段线
//=Parameter: geRay[in] 射线(位于多段线的OCS平面上)
//=Parameter: arptIntersect[in] 返回的交点(坐标系为多段线的OCS坐标系)
//=Parameter: tol[in] 容差
//-----------------------------------------------------------------------------+
static void IntersectWithGeRay(const AcDbPolyline *pPoly, const AcGeRay2d &geRay, AcGePoint2dArray& arptIntersect, double tol = 1.0E-7)
{arptIntersect.removeAll();//设置容差,该容差为两点相同时的容差AcGeTol geTol;geTol.setEqualPoint(tol);// 多段线的每一段分别与射线计算交点AcGePoint2d pt2d;for (int i = 0; i < pPoly->numVerts(); i++){if (i < pPoly->numVerts() - 1 || pPoly->isClosed() == Adesk::kTrue){double dBulge = 0;pPoly->getBulgeAt(i, dBulge);if (fabs(dBulge) < 1.0E-7){// 构建几何类的线段来计算交点AcGeLineSeg2d geLine;Acad::ErrorStatus es = pPoly->getLineSegAt(i, geLine);AcGePoint2d ptIntersect;if (geLine.intersectWith(geRay, ptIntersect, geTol) == Adesk::kTrue){if (FindPoint(arptIntersect, ptIntersect, tol) < 0)arptIntersect.append(ptIntersect);}}else{// 构建几何类的圆弧来计算交点AcGeCircArc2d geArc;pPoly->getArcSegAt(i, geArc);AcGePoint2d pt1, pt2;int iCount = 0;if (Adesk::kTrue == geArc.intersectWith(geRay, iCount, pt1, pt2, geTol)){if (FindPoint(arptIntersect, pt1, tol) < 0)arptIntersect.append(pt1);if (iCount > 1 && FindPoint(arptIntersect, pt2, tol) < 0)arptIntersect.append(pt2);}}}}
}// 点是否是多段线的顶点
static bool PointIsPolyVert(AcDbPolyline *pPoly, const AcGePoint2d &pt, double tol)
{AcGeTol geTol;geTol.setEqualPoint(tol);AcGePoint2d ptVert;for (int i = 0; i < (int)pPoly->numVerts(); i++){pPoly->getPointAt(i, ptVert);if (ptVert.isEqualTo(pt, geTol)){return true;}}return false;
}// 从数组中过滤掉重复点
static void FilterEqualPoints(AcGePoint2dArray &points, double tol = 1.0E-7)
{AcGeTol geTol;geTol.setEqualPoint(tol);for (int i = points.length() - 1; i > 0; i--){for (int j = 0; j < i; j++){if (points[i].isEqualTo(points[j],geTol)){points.removeAt(i);break;}}}
}// 从数组中过滤掉某个点
static void FilterEqualPoints(AcGePoint2dArray &points, const AcGePoint2d &pt, double tol = 1.0E-7)
{AcGeTol geTol;geTol.setEqualPoint(tol);for (int i = points.length() - 1; i >= 0; i--)if (points[i].isEqualTo(pt, geTol))points.removeAt(i);
}//-----------------------------------------------------------------------------+
//=Description: 判断点是否在多段线内部
//=Return: 0多段线外,1多段线内,2多段线上
//=Parameter: pPoly[in]
//=Parameter: ptPickWcs[in]
//=Parameter: tol[in]
//-----------------------------------------------------------------------------+
int IsPointInPoly(AcDbPolyline *pPoly, const AcGePoint3d &ptPickWcs, double tol = 1.0E-7)
{if(!pPoly || !pPoly->isClosed())return POINT_POLY_OUTSIDE;AcGeTol geTol;geTol.setEqualPoint(tol);//转换坐标,将点转为ECS坐标系AcGePoint3d ptPick;acdbWcs2Ecs(asDblArray(ptPickWcs), asDblArray(ptPick), asDblArray(pPoly->normal()), false);//判断点和多段线平面是否共面double dElevation = pPoly->elevation();if (fabs(dElevation - ptPick.z) > tol)return POINT_POLY_OUTSIDE;//如果点到多段线的最近点和给定的点重合,表示点在多段线上AcGePoint3d ptClosestWcs;pPoly->getClosestPointTo(ptPickWcs, ptClosestWcs);if (ptPickWcs.isEqualTo(ptClosestWcs, geTol))return POINT_POLY_ONEDGE;//转换最近点为ECS坐标系下AcGePoint3d ptClosest;acdbWcs2Ecs(asDblArray(ptClosestWcs), asDblArray(ptClosest), asDblArray(pPoly->normal()), false);// 第一个射线的方向是从最近点到当前点,起点是当前点// 射线的起点是pt,方向为从最近点到pt,如果反向做判断,则最近点距离pt太近的时候,// 最近点也会被作为一个交点(这个交点不太容易被排除掉)AcGeVector2d vtRay((ptPick - ptClosest).x, (ptPick - ptClosest).y);AcGeRay2d geRay(AcGePoint2d(ptPick.x, ptPick.y), vtRay);// 判断点和多段线的位置关系while (true){bool bContinue = false;AcGePoint2dArray arptIntersect;IntersectWithGeRay(pPoly, geRay, arptIntersect, 1.0E-4);FilterEqualPoints(arptIntersect, 1.0E-4);// IntersectWith函数经常会得到很近的交点,这些点必须进行过滤if (arptIntersect.length() == 0)return POINT_POLY_OUTSIDE;// 没有交点,表示点在多段线的外部else{//特殊情况1:过滤掉由于射线被反向延长带来的影响,当pt距离最近点比较近的时候,//最近点竟然被当作一个交点,所以,首先删除最近点(如果有的话)FilterEqualPoints(arptIntersect, AcGePoint2d(ptClosest.x, ptClosest.y));//特殊情况2:如果某个交点与最近点在给定点的同一方向,要去掉这个点//,这个点明显不是交点,还是由于intersectwith函数的Bugfor (int i = arptIntersect.length() - 1; i >= 0; i--){if ((arptIntersect[i].x - ptPick.x) * (ptClosest.x - ptPick.x) >= 0 &&(arptIntersect[i].y - ptPick.y) * (ptClosest.y - ptPick.y) >= 0)arptIntersect.removeAt(i);}for (i = 0; i < arptIntersect.length(); i++){if (PointIsPolyVert(pPoly, arptIntersect[i], 1.0E-4)) // 只要有交点是多段线的顶点就重新进行判断{// 处理给定点很靠近多段线顶点的情况(如果与顶点距离很近,就认为这个点在多段线上,因为这种情况没有什么好的判断方法)if (PointIsPolyVert(pPoly, AcGePoint2d(ptPick.x, ptPick.y), 1.0E-4))return POINT_POLY_ONEDGE;// 将射线旋转一个极小的角度(2度)再次判断(假定这样不会再通过上次判断到的顶点)vtRay = vtRay.rotateBy(0.035);geRay.set(AcGePoint2d(ptPick.x, ptPick.y), vtRay);bContinue = true;break;}}if (!bContinue){if (0 == arptIntersect.length() % 2)return POINT_POLY_OUTSIDE;elsereturn POINT_POLY_INSIDE;}}}
}
3.2 测试代码
void CmdPtInPoly()
{struct resbuf* rb = NULL;rb = acutBuildList(RTDXF0, _T("LWPOLYLINE"), RTNONE);TCHAR* prompts[2] = { _T("\n请选择了一个实体:"),_T("\n取消了一个实体") };ads_name ssPick;if (RTNORM == acedSSGet(_T(":S:$-M"), prompts, NULL, rb, ssPick)){ads_name ent;if (RTNORM == acedSSName(ssPick, 0, ent)){AcDbObjectId id;acdbGetObjectId(id, ent);AcDbPolyline* pPoly;if (Acad::eOk == acdbOpenObject(pPoly, id, AcDb::kForRead)){ads_point ptRet;while (RTNORM == acedGetPoint(NULL, _T("\n请任意点选一点:"), ptRet)){//判断点是否在多段线以内int iRelation = IsPointInPoly(pPoly, Ucs2Wcs(ptRet));if (POINT_POLY_INSIDE == iRelation)acutPrintf(_T("\n\t点在多段线内"));else if (POINT_POLY_ONEDGE == iRelation)acutPrintf(_T("\n\t点在多段线上"));else if (POINT_POLY_OUTSIDE == iRelation)acutPrintf(_T("\n\t点在多段线外"));}pPoly->close();}}acedSSFree(ssPick);}acutRelRb(rb);
}
4 实现效果

相关文章:

ObjectARX如何判断点和多段线的关系
目录 1 基本思路2 相关知识点2.1 ECS坐标系概述2.2 其他点坐标转换接口2.3 如何获取多段线的顶点ECS坐标 3 实现例程3.1 接口实现3.2 测试代码 4 实现效果 在CAD的二次开发中,点和多段线的关系是一个非常重要且常见的问题,本文实现例程以张帆所著《Objec…...

四、DRF序列化器create方法与update方法
上一章: 二、Django REST Framework (DRF)序列化&反序列化&数据校验_做测试的喵酱的博客-CSDN博客 下一章: 五、DRF 模型序列化器ModelSerializer_做测试的喵酱的博客-CSDN博客 一、背景 1、创建请求,post,用户输入…...

洛谷P8792 最大公约数
[蓝桥杯 2022 国 A] 最大公约数 题目描述 给定一个数组,每次操作可以选择数组中任意两个相邻的元素 x , y x, y x,y 并将其中的一个元素替换为 gcd ( x , y ) \gcd(x, y) gcd(x,y),其中 gcd ( x , y ) \gcd(x, y) gcd(x,y) 表示 x x x 和 y…...
【SpringBoot集成Nacos+Dubbo】企业级项目集成微服务组件,实现RPC远程调用
文章目录 一、需求环境/版本 二、须知2.1、什么是RPC?2.2、什么是Dubbo?2.3、什么是Nacos? 三、普通的SpringBoot项目集成微服务组件方案(笔者给出两种)方案一(推荐)1、导入maven依赖࿰…...

MySQL主从同步(开GTID)
目录 一、搭建简单的主从同步 二、mysql删除主从(若没有配置过可以不用进行这一步) 1、停止slave服务器的主从同步 2、重置master服务 三、开启GTID 1、Master配置 2、Slave配置 一、搭建简单的主从同步 GTID原理:http://t.csdn.cn/g…...

打造精细化调研,这些产品榜上有名,你用了吗?
调查问卷是一种流行的数据收集工具,研究人员、营销人员和企业使用它来征求目标受众的反馈意见。调查问卷工具使创建、分发和分析调查问卷的过程变得更加简单和高效。想要做好一份调查问卷,选择一款好用的工具是少不了的。不过,在众多的问卷工…...
[golang gin框架] 37.ElasticSearch 全文搜索引擎的使用
一.全文搜索引擎 ElasticSearch 的介绍,以及安装配置前的准备工作 介绍 ElasticSearch 是一个基于 Lucene 的 搜索服务器,它提供了一个 分布式多用户能力的 全文搜索引擎,基于 RESTful web 接口,Elasticsearch 是用 Java 开发的,并作为 Apach…...

赋的几个发展阶段
赋,起源于战国,形成于汉代,是由楚辞衍化出来的,也继承了《诗经》讽刺的传统。关于诗和赋的区别,晋代文学家陆机在《文赋》里曾说: 诗缘情而绮靡,赋体物而浏亮。 也就是说,诗是用来抒发主观感情…...
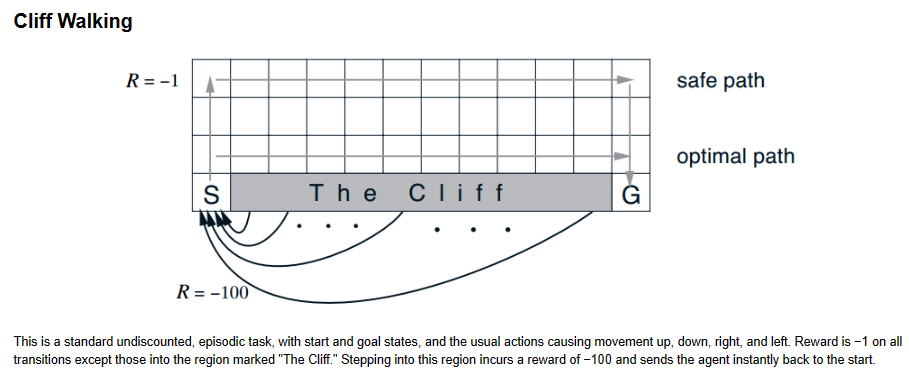
Model-Free TD Control: Sarsa
import time import random # 相对于Q 效果会差一些 class Env():def __init__(self, length, height):# define the height and length of the mapself.length lengthself.height height# define the agents start positionself.x 0self.y 0def render(self, frames50):fo…...
CloudBase CMS的开发注意事项
引言 在进行基于云开发的微信小程序开发时为了减轻工作量打算用CloudBase CMS来减轻工作量,随后去了解并体验了CloudBase CMS的使用,总体来说还有些许问题没有解决,对减轻后台管理工作并没有起到很大的作用。 项目情景 使用CloudBase CMS来管…...

大佬联合署名!反对 ACL 设置匿名期!
夕小瑶科技说 原创 作者 | 智商掉了一地、Python 近日,自然语言处理领域的多位知名学者联合发起了一项反对 ACL 设置匿名期的联合署名行动,包括著名学者 William Wang 和 Yoav Goldberg 在内,还有Christopher Potts、Hal Daume、Luke Zettl…...
【JavaSE】Java基础语法(十四):Static
文章目录 概述特点与应用注意事项为什么一个静态方法中只能访问用static修饰的成员? 概述 Java中的static是一个修饰符(也可称关键字),可以用于修饰变量、方法和代码块。 特点与应用 static修饰的成员具有以下特点: 被类的所有对…...

1.Linux初识
在 Linux 系统中,sudo 是一个重要的命令,可以允许普通用户以管理员权限来运行特定的命令。通过 sudo 命令,普通用户可以暂时获取管理员权限,执行需要管理员身份才能执行的操作。 下面是一些关于 sudo 命令的用法: 以管…...
进程(二)
这一节我们写个MFC剪切板程序 1.下载相应的组件 工具->工具视图,因为之前已经下载过一部分了,这里如果创建MFC报错的话,就要把没下载的补上 此项目需要MFC库 解决方法 2.创建MFC程序 3.打开资源视图,直接在菜单栏顶部搜索…...
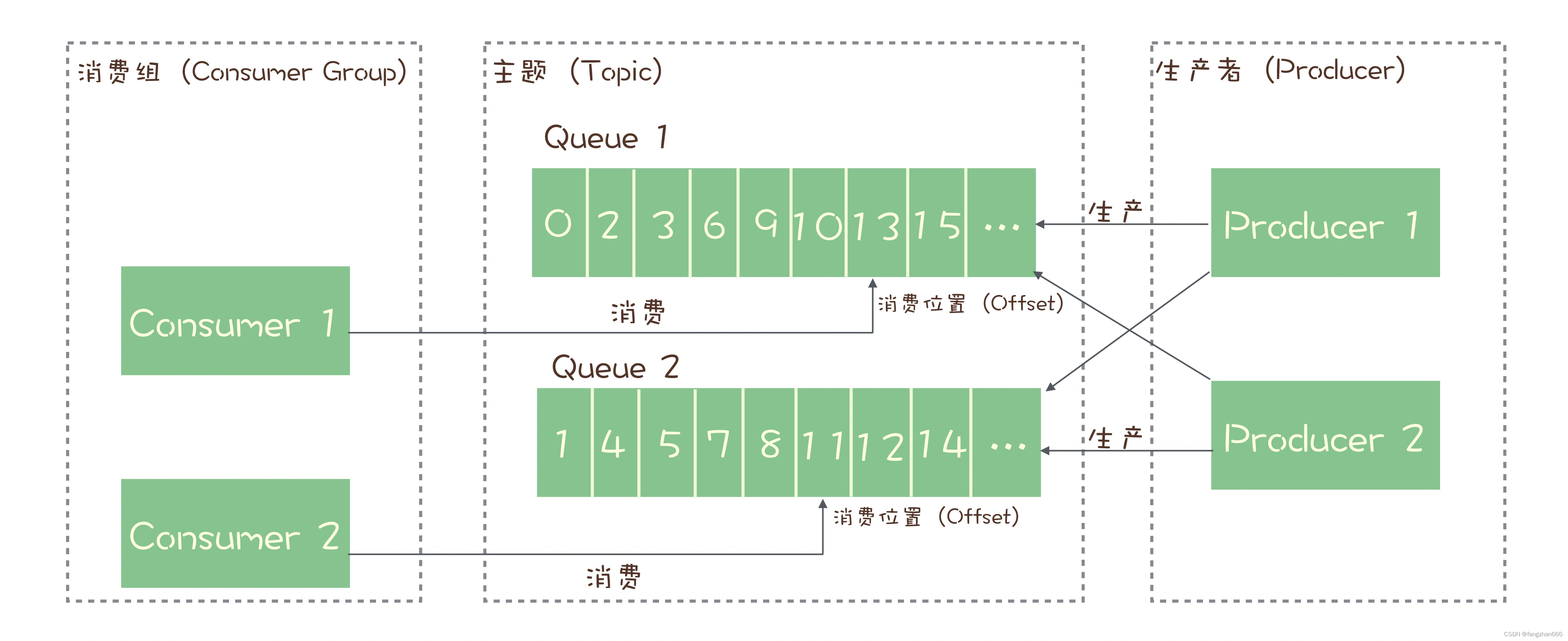
《消息队列高手课》课程笔记(二)
消息模型:主题和队列有什么区别? 两类消息模型 早期的消息队列,就是按照“队列”的数据结构来设计的。 生产者(Producer)发消息就是入队操作,消费者(Consumer)收消息就是出队也就是…...

以“智”提质丨信创呼叫
随着人工智能、大数据、云计算等新兴技术飞速发展,呼叫中心、全媒体智能客服等现已被广泛应用于多个行业领域。其中,呼叫中心作为政企对外服务的重要窗口,已从“传统电话营销”发展到“智能呼叫中心”阶段,以客户服务为核心&#…...

Pool与PG的说明以及Ceph的IO流程
Pool与PG的说明以及Ceph的IO流程 Pool与PG Ceph中的数据是以对象的形式存储在存储池(pool)中的。每个存储池都被划分为若干个存储组(PG),每个存储组同时也是一个数据分片(shard)。存储组是Ceph用来实现数据的分布式存储和高可用的重要组成部分。每个存储组包含若干…...

20230529_Hadoop_集群操作命令
HDFS_集群操作命令: 一、集群启停命令 # 启动Hadoop的HDFS进程start-dfs.sh# 关闭Hadoop的HDFS进程stop-dfs.sh# 单独关闭某一个进程hadoop-daemon.sh start[/stop] namenode[/datanode/secondarynamenode]二、HDFS文件系统的基本信息 数据的路径表达方式ÿ…...
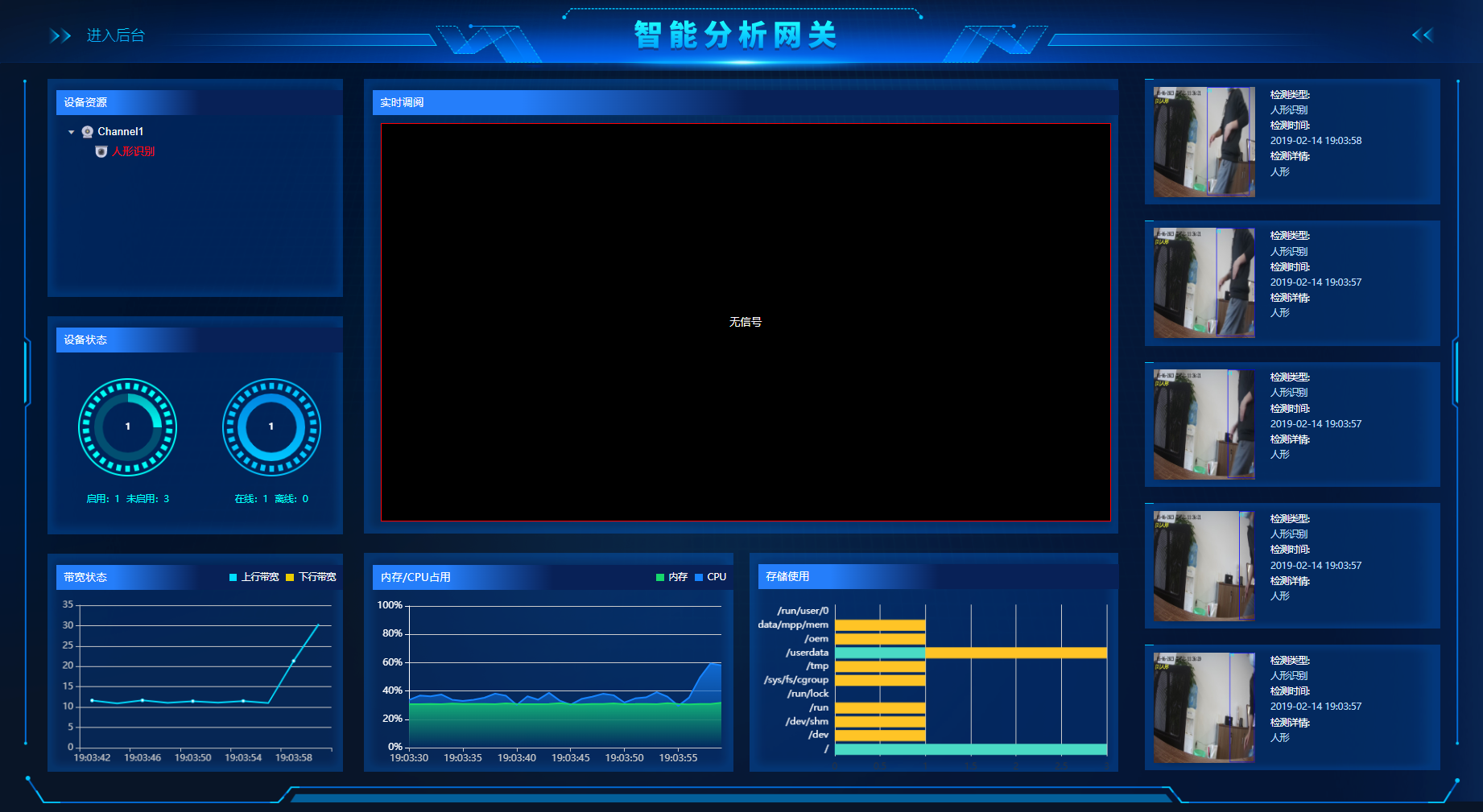
边缘计算AI硬件智能分析网关V1版的接入流程与使用步骤
我们的AI边缘计算网关硬件——智能分析网关目前有两个版本:V1版与V2版,两个版本都能实现对监控视频的智能识别和分析,支持抓拍、记录、告警等,在AI算法的种类上和视频接入上,两个版本存在些许的区别。V1的基础算法有人…...
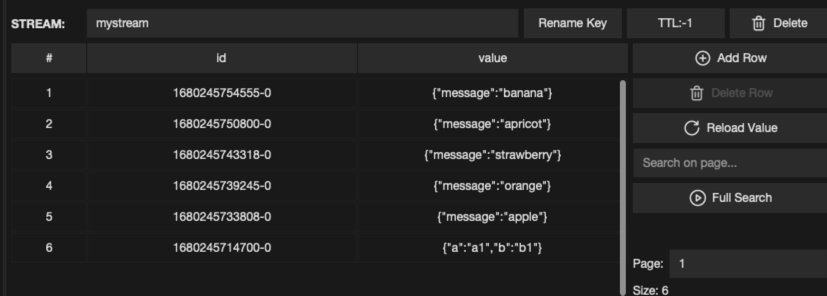
【redis】Stream、String 超详细介绍
文章目录 一、Stream1.1 写入数据XADD条目 ID 的格式 1.2 获取数据XRANGE 和 XREVRANGEXREAD 监听新条目非阻塞形式阻塞形式 1.3 消费者组XGROUP 创建消费者组XREADGROUP 通过消费者组消费XACK 确认消息消费者组示例 1.4 XPENDING 和 XCLAIM 认领 其他消费者 的待处理消息XPEND…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
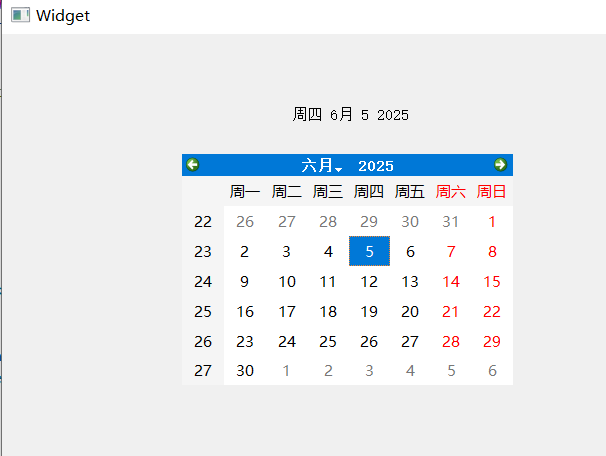
【QT控件】显示类控件
目录 一、Label 二、LCD Number 三、ProgressBar 四、Calendar Widget QT专栏:QT_uyeonashi的博客-CSDN博客 一、Label QLabel 可以用来显示文本和图片. 核心属性如下 代码示例: 显示不同格式的文本 1) 在界面上创建三个 QLabel 尺寸放大一些. objectName 分别…...
