【线性dp必学四道题】线性dp四道经典例题【最长上升子序列】、【最长公共子序列】、【最长公共上升子序列(maxv的由来)】【最长公共子串】
【最长上升子序列】、【最长公共子序列】、【最长公共上升子序列】
- 最长上升子序列
- f[i] 表示以i结尾的最长子序列
- 最长公共子序列
- f[i][j] 表示 a前i 和 b前j个 最长公共长度
- 最长公共上升子序列
- f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合
- 最长公共子串
最长上升子序列
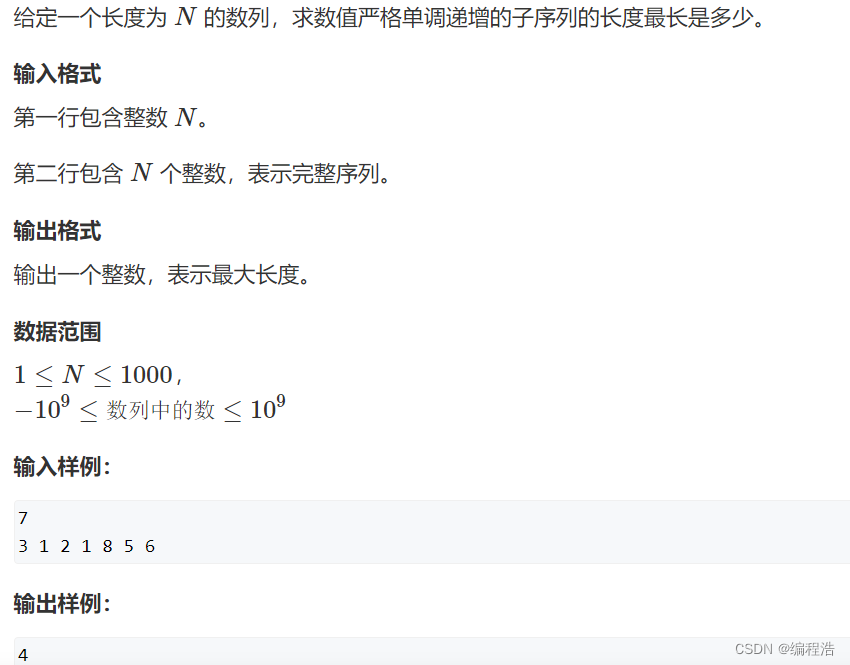
f[i] 表示以i结尾的最长子序列
由于我们遍历到i时候
我们需要比较i前面的数据
我们发现如果i 大于 j
那么i就可以拼接在 j 后面
如果f[j] 就是j最长的了
那就
f[i] = f[j] + 1的长度
所以
f[i] 表示以i结尾的最长子序列
#include<iostream>using namespace std;const int N = 1100;int a[N];
int f[N];
int res = 0;
int n;int main()
{cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];a[0] = -0x3f3f3f3f;for(int i = 1; i <= n; i++){for(int j = 0; j <= i ; j++){if(a[j] < a[i])f[i] = max(f[i],f[j]+1);res = max(res,f[i]);}}cout << res;return 0;
}
最长公共子序列

f[i][j] 表示 a前i 和 b前j个 最长公共长度
#include<iostream>using namespace std;const int N = 1010;int f[N][N];
char a[N],b[N];
int n,m;int main()
{cin >> n >> m;cin >> a+1 >> b+1;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){if(a[i]==b[j]){f[i][j] = f[i-1][j-1]+1;}else{f[i][j] = max(f[i-1][j],f[i][j-1]);}}}cout << f[n][m];return 0;
}
最长公共上升子序列
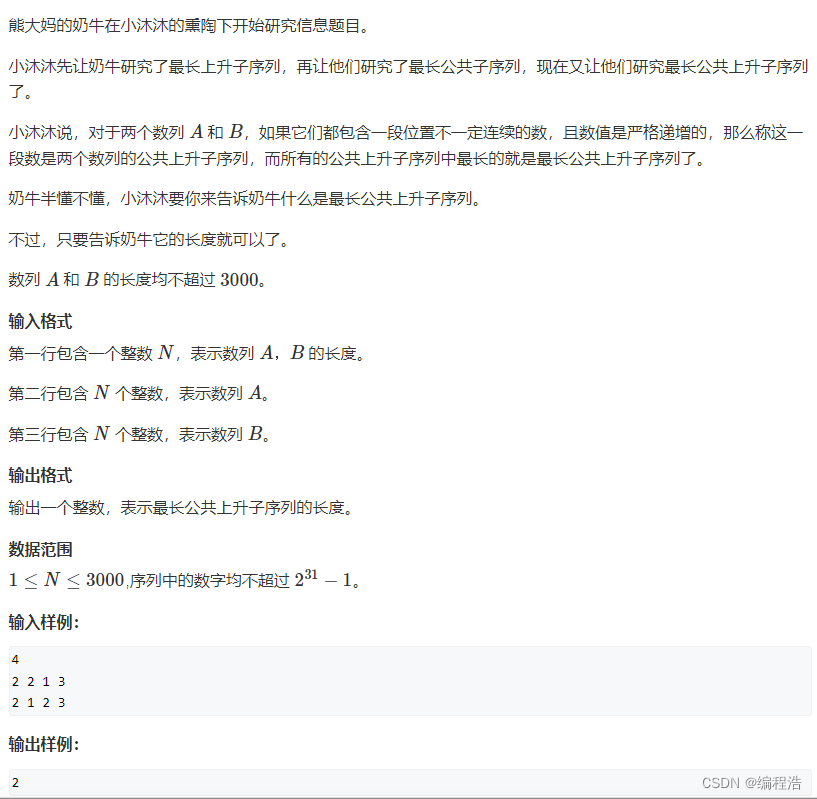
f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合
这道题如何理解?
- 记住f[i][j] 表示什么
- 当b的j和i 相等时,我们常规思路是就在b数组中按着第一道题的逻辑 循环遍历之前的值,但是这样是麻烦的。我们需要一种方法,不需要遍历就知道之前的最大值,可以定义一个变量maxv,如果i和j相等,直接等于maxv,如果不相等,那么f[i][j] = f[i-1][j]
- 如果a[i]>b[j]
那么maxv = max(maxv,f[i-1][j]+1);
maxv的由来

#include<iostream>using namespace std;const int N = 3030;int f[N][N];
int a[N],b[N];
int n;int main()
{cin >> n;for(int i = 1; i <= n; i++) cin >> a[i];for(int i = 1; i <= n; i++) cin >> b[i];for(int i = 1; i <= n; i++){int maxv = 1;for(int j = 1; j <= n; j++){f[i][j] = f[i-1][j];if(a[i]==b[j]){f[i][j] = maxv;}if(a[i]>b[j])maxv = max(maxv,f[i-1][j]+1);}}int ans = 0;for(int i = 0; i <= n; i++){ans = max(f[n][i],ans);}cout << ans;return 0;
}
最长公共子串

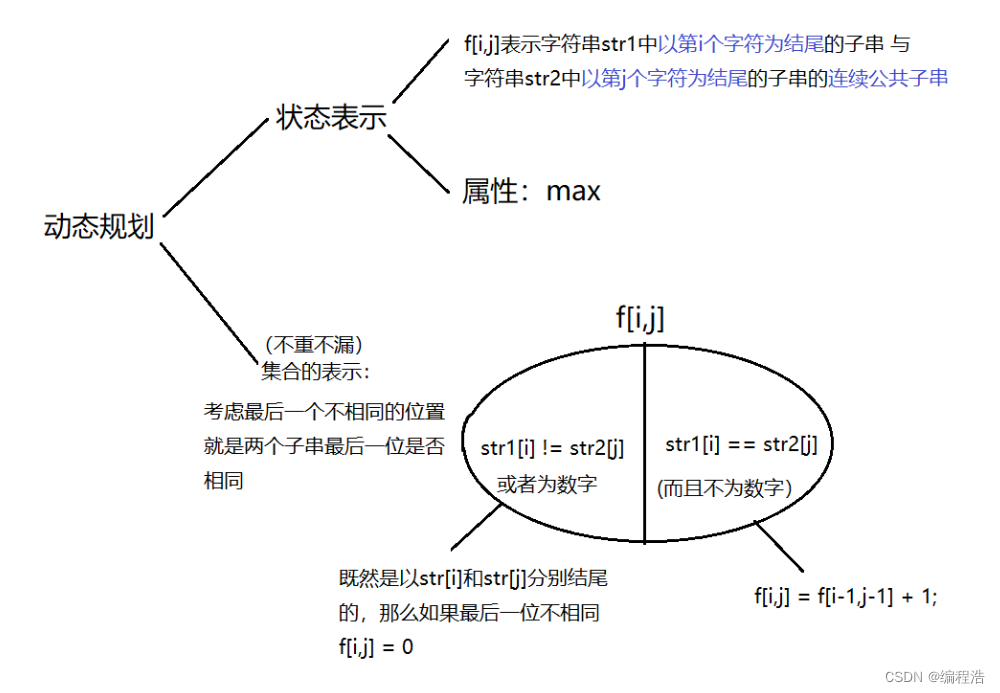
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e4 + 10;
char str1[N], str2[N];int f[N][N];//注意空间限制为256MB,即为2^(8 + 20) = 2^28个字节,
//而一个int型变量占4个字节,那么最多有2^26个int变量,大约为64000000个变量,而此时定义f[N][N]最多有大于1e8个变量,会爆内存
//更何况还有存字符串的空间int main()
{cin >> str1 + 1 >> str2 + 1; int len1 = strlen(str1 + 1), len2 = strlen(str2 + 1);int res = 0;for (int i = 1; i <= len1; i++){//如果最后一位为数字if (str1[i] >= '0' && str1[i] <= '9'){for (int j = 1; j <= len2; j++)f[i][j] = 0;continue; }for (int j = 1; j <= len2; j++){//如果最后一位相同且不为数字if (str1[i] == str2[j])f[i][j] = f[i - 1][j - 1] + 1;else f[i][j] = 0;res = max(res, f[i][j]);}}cout << res << endl;return 0;
}
观察我们在状态计算的过程,第i层循环的值,仅与第i-1层循环的值有关
我们可以联想到01背包的优化,利用滚动数组来简化空间复杂度
既然要用到删除一维空间的优化方法,一定要注意:
二维中:f[i][j] = f[i - 1][j - 1] + 1;
在一维中,由于f[j] = f[j - 1],小的j已经被更新,那么就不是上一层(i-1)的数据了
所以必须从大到小遍历
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e4 + 10;
char str1[N], str2[N];int f[N];int main()
{cin >> str1 + 1 >> str2 + 1; int len1 = strlen(str1 + 1), len2 = strlen(str2 + 1);int res = 0;//用于保存答案for (int i = 1; i <= len1; i++){//如果最后一位为数字if (str1[i] >= '0' && str1[i] <= '9'){for (int j = 1; j <= len2; j++)f[j] = 0;continue; }for (int j = len2; j >= 1; j--){//如果最后一位相同且不为数字if (str1[i] == str2[j])f[j] = f[j - 1] + 1;else f[j] = 0;res = max(res, f[j]);}}cout << res << endl;return 0;
}
相关文章:

【线性dp必学四道题】线性dp四道经典例题【最长上升子序列】、【最长公共子序列】、【最长公共上升子序列(maxv的由来)】【最长公共子串】
【最长上升子序列】、【最长公共子序列】、【最长公共上升子序列】 最长上升子序列f[i] 表示以i结尾的最长子序列 最长公共子序列f[i][j] 表示 a前i 和 b前j个 最长公共长度 最长公共上升子序列f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合 最长公共子…...

追寻幸福:探索幸福的关键特征和行为
目录 1. 积极的心态 2. 良好的人际关系 3. 自我接纳和自尊 4. 追求意义和目标 5. 健康的身心状态 6. 感知和实现个人价值 幸福是一个主观的感受,因此不同的人对于幸福的定义和追求方式可能会有所不同。然而,有一些共同的特点和行为模式,…...

Redis-02-集群
一、redis5搭建集群 1.1、案例:搭建6台redis主机,配置如下 redis并发量:https://www.gxlcms.com/redis-350423.html主机IP:192.168.168.60~65修改redis配置文件hash槽移动,槽内的数据也随之移动 [root60 ~]# vim /e…...
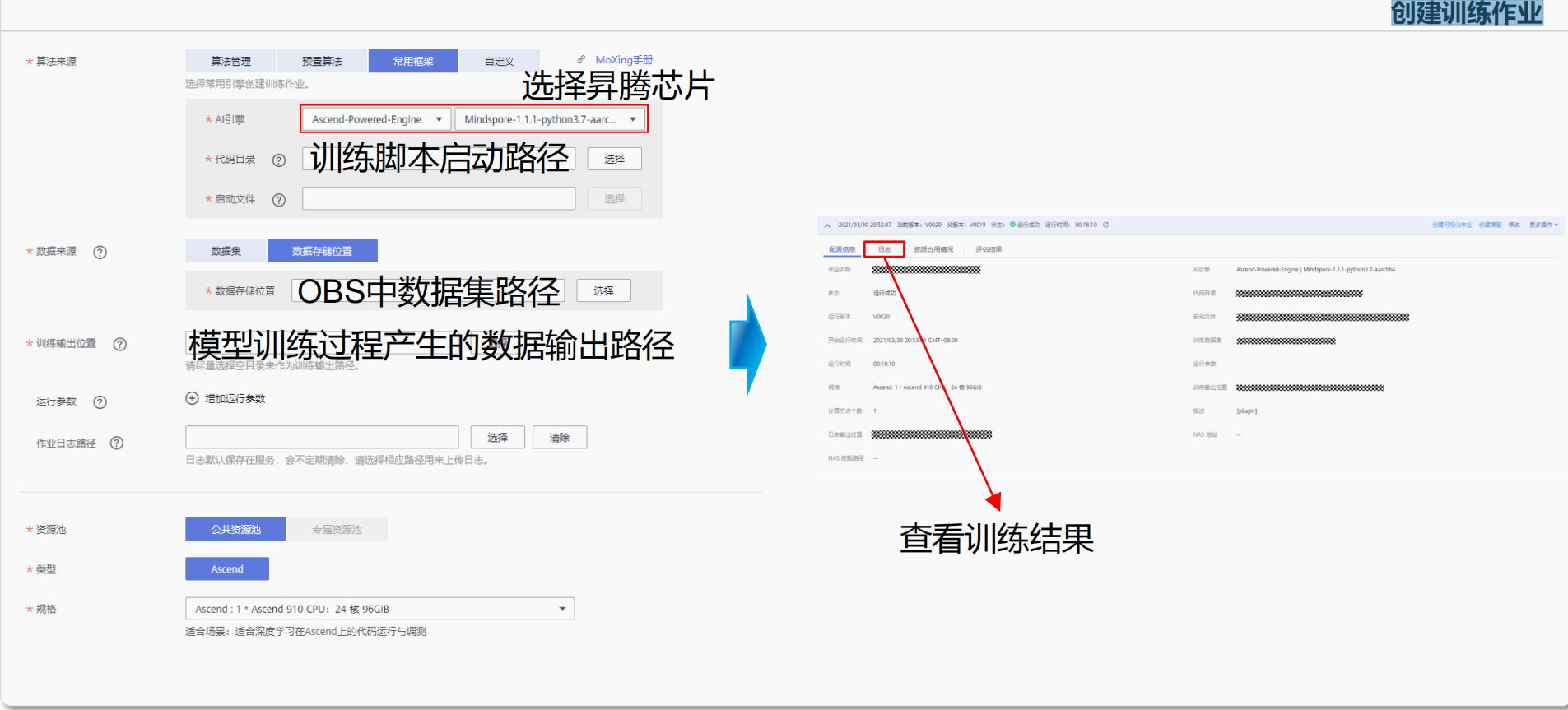
【2023 · CANN训练营第一季】MindSpore模型快速调优攻略 第三章——MindSpore云上调试调优
1.ModelArts云上调试调优 ModelArts密钥初始化 详细教程: 初始化OBS服务 创建训练作业 2.MindSpore IDE插件效率提升 通过智能代码块推荐、代码自动补全等特性,提升MindSpore脚本开发效率,对接ModelArts云服务,实现模型训…...
python笔记17_实例演练_二手车折旧分析p2
…… 书接上文 4.车辆等级维度 探查车龄为5年的车辆,折旧价值与车辆等级的关系。 # 筛选出车龄为5的数据创建新表 data_age5 data[data[age] 5] data_age5 # 分组聚合计算均值 data_car_level data_age5.groupby(car_level_name)[lowest_price].mean().reset…...

android 12.0长按Power弹出关机对话框去掉屏幕截图和紧急呼救功能
1.概述 在12.0的系统长按关机键,会弹出关机的对话框,关机对话框里面由关机重启截图和紧急呼叫等功能,而由于开发功能需求要求去掉屏幕截图和紧急呼叫等功能,所以就要先找到关机对框的代码 然后实现功能 功能分析: 长按电源键弹出关机对话框,通过adb shell命令发现 就是f…...

2023年下半年软考高级需要报班吗?
首先,对于软考高级考试报班与否的问题,需要根据自身的情况来做出决定。如果你有较强的自学能力,且具备丰富的实际工作经验和技术知识,那么不报班也完全可以自学备考。但如果你对软件工程的知识掌握程度较低,或者时间紧…...

使用WordPress提高企业敏捷性
喜欢WordPress的原因有很多:该平台非常适合内容管理以及控制预算。此外, 在 提高开发效率和简化项目管理方面,WordPress可以通过多种方式提供帮助。 对于任何企业业务,目标始终是在不影响质量的情况下更快地启动项目、发布修复和…...

SSM编程---Day 07
目录 SpringMVC 一、概念 二、springMVC的请求处理流程 三、mvc:annotation-driven 标签的作用 四、HandlerMapping、Handler和HandlerAdapter的介绍 五、SpringMVC 体系结构 六、SpringMVC的常用注解 七、view和controller之间的传值 SpringMVC 一、概念 1、 Spring…...
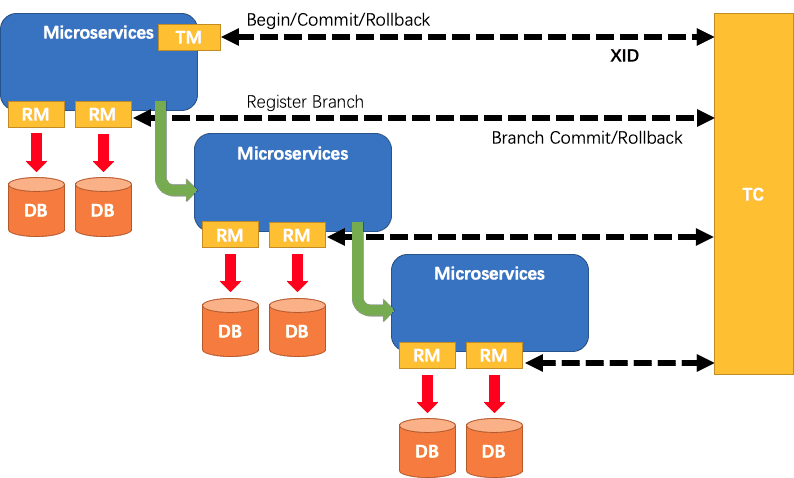
Seata术语
1.什么是Seata Seata是一款开源的分布式事务解决方案,致力于在微服务架构下提供高性能和简单易用的分布式事务服务。 官网 2.Seata能干嘛 一个典型的分布式事务过程 分布式事务处理过程的一ID三组件模型: Transaction ID XID 全局唯一的事务ID三组…...

【Axure教程】通过文本框维护下拉列表选项
下拉列表(Dropdown List)是一种常见的用户界面元素,用于提供一组选项供用户选择。它通常以一个展开的列表形式出现,用户可以点击或选择列表中的一个选项。一般来说,他的选项值是由系统代码组成的,所以一般是…...
)
【C++】基础知识--输入/输出(5)
前面部分的示例程序几乎没有提供与用户的交互(如果有的话)。他们只是在屏幕上打印简单的值,但标准库提供了许多其他方式通过其输入/输出功能与用户交互。本节将简要介绍一些最有用的方法。 cin标准输入cout标准输出cerr标准错误(输…...
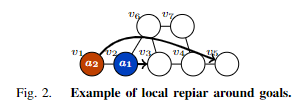
经典文献阅读之--PIBT(基于可见树的实时规划方案)
0. 简介 作为路径规划而言,不单单有单个机器人自主路径规划,近年来随着机器人行业的兴起,多机器人自主路径规划也越来越受到关注,对于多智能体寻路(MAPF)。一般的操作会给定一个地图、机器人集群、以及它们的初始位置和目的地&am…...

SAP-MM-计算方案字段解析
01、 “步骤”:标识此条件类型在计算方案中的顺序编号,此编号会影响到后续业务中条件类型的排序,不同条件类型之间的编号最好间隔大一些,这样设置便于以后对计算方案进行扩展; 02、 “计数器”࿱…...

go-gf框架两个表以事务方式写入示例
下面是对每一行代码的中文解释: // 创建数据库连接对象 var tx gdb.TX这行代码声明了一个名为tx的变量,类型为gdb.TX,表示数据库事务对象。 // 开启事务 if tx, err g.DB().Ctx(ctx).Begin(ctx); err nil {这行代码通过在数据库连接&…...

2023-5-31第三十一天
conform顺从,遵从,一致 squeeze挤压 proprietary专卖权,专利的,所有的 endeavor努力,尽力 comprise由...组成,包含 compose组成,写作 compact小型的 consult咨询,查阅 expan…...
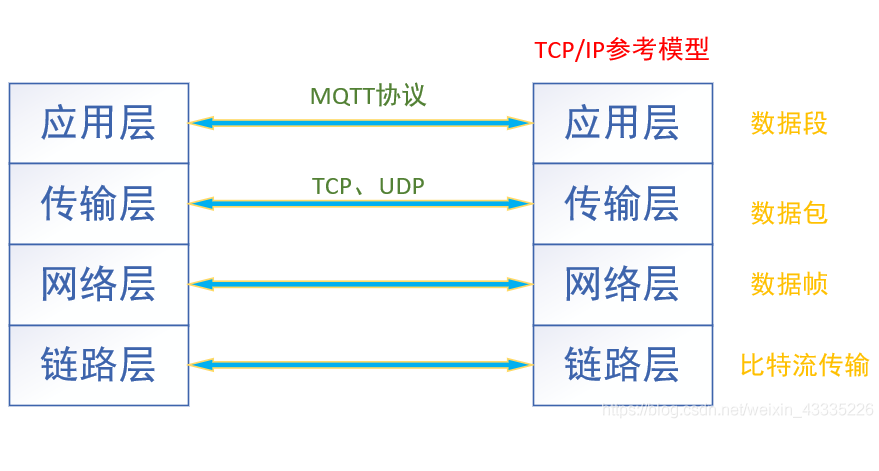
什么是MQTT?mqtt协议和http协议区别
摘要: 什么是MQTT?MQTT(Message Queuing Telemetry Transport)译为:消息队列遥测传输,是一种轻量级的通讯协议,用于在网络上传输消息。MQTT 最初由 IBM 发布,后来成为 OASIS…...
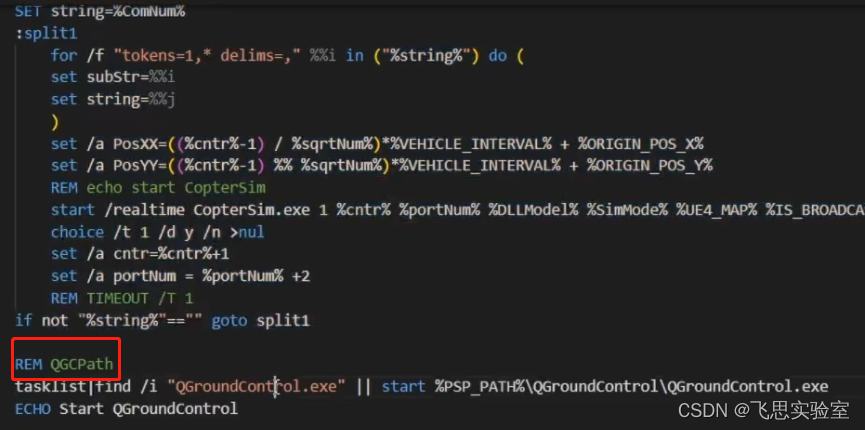
平台使用篇 | 批处理(bat)脚本使用教程(四)
导读 一个开启多机软件在环仿真的批处理文件 (对应卓面RflyTools文件夹中SITLRun快捷方式),双击它,输入想要生成的飞机数量,即可生成多机软件在环仿真,等待RflySim3D显示3DFixed 4/4,然后可通过QGC控制飞机起飞。运行…...

接口的讲解
在这里之前我想童鞋们都学习过了springmvc。mybatis-plus。Springboot等一些框架 那么下面我们就整合这些框架 我们通过写crud这些接口 写接口的第一步就是引入pom文件 在pom文件里引入一下几种依赖 引入父级工程 thymeleaf导入模版工具类 SpringMVCjar包文件 热部署工具 l…...
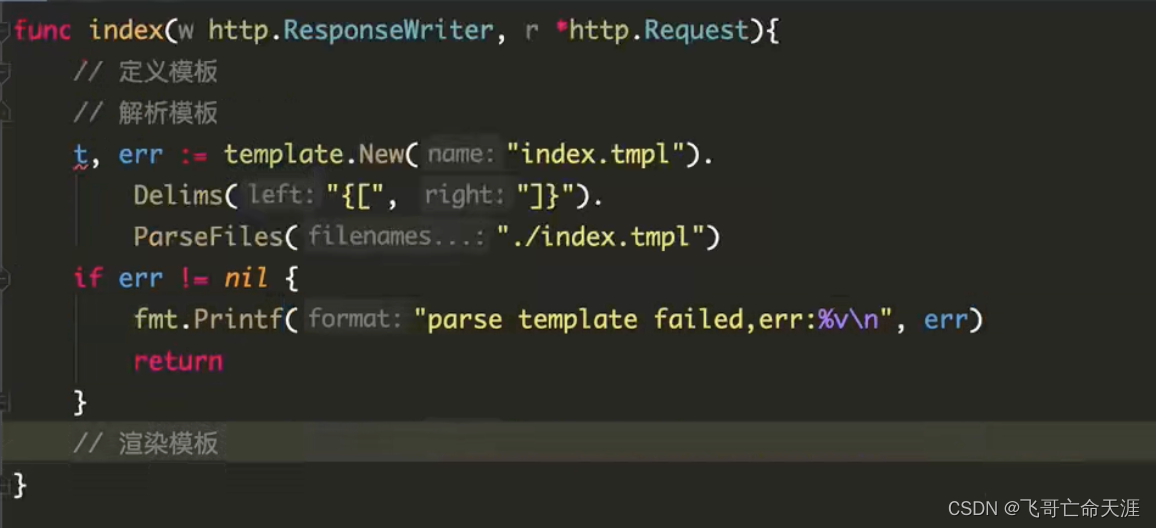
G0第21章 :gin框架介绍、RESTful API、Gin渲染
G0第21章 :gin框架 01 内容介绍 https://gin-gonic.com/zh-cn/docs/ web本质 Web是基于HTTP协议进行交互的应用网络Web就是通过使用浏览器/APP访问的各种资源 package mainimport ("fmt""net/http" )func sayHello(w http.ResponseWriter, r…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
