[Daimayuan] 树(C++,动态规划,01背包方案数)
有一棵 n n n 个节点的以 1 1 1 号点为根的有根树。现在可以对这棵树进行若干次操作,每一次操作可以选择树上的一个点然后删掉连接这个点和它的儿子的所有边。
现在我们想知道对于每一个 k k k ( 1 ≤ k ≤ n 1≤k≤n 1≤k≤n),最少需要多少次操作能让图中恰好存在 k k k 个联通块。
输入格式
第一行输入一个正整数 n n n。
第二行输入 n − 1 n−1 n−1 个整数 f 1 , f 2 , . . . , f n − 1 f_1,f_2,...,f_{n−1} f1,f2,...,fn−1, f i f_i fi 表示 i + 1 i+1 i+1 号点的父亲,保证 1 ≤ f i ≤ i 1≤f_i≤i 1≤fi≤i。
输出格式
输出 n n n 个整数,第 i i i 个数表示 k = i k=i k=i 时的答案,如果无法让图中恰好存在 i i i 个联通块,则输出 -1。
样例输入1
6
1 2 1 1 2
样例输出1
0 -1 1 1 -1 2
数据规模
共 10 10 10 个测试点。
测试点 1 , 2 , 3 1,2,3 1,2,3 满足 n ≤ 20 n≤20 n≤20。
测试点 4 , 5 , 6 4,5,6 4,5,6 满足 n ≤ 100 n≤100 n≤100。
对于所有数据,满足 1 ≤ n ≤ 3000 1≤n≤3000 1≤n≤3000。
解题思路
对于一棵树来说,删去任意一条边都会使连通块数目 + 1 +1 +1。
那么要判断能否得到 k k k个连通块,我们只需要判断能否恰好删去 k − 1 k-1 k−1条边。
题目要求操作为:删除一个节点与子节点之间的所有边。
那么统计每个节点的子节点数目,然后就变为了01背包可行性问题:
每一个节点都是一个物品,问能否恰好装满容量为 k − 1 k-1 k−1的背包?
for (int i = 1; i <= n; i++) {//尝试每一个物品for (int j = 0; j < n; j++) {//尝试新的重量组合if (j - items[i] >= 0)ans[i][j] = ans[i - 1][j] || ans[i - 1][j - items[i]];elseans[i][j] = ans[i - 1][j];}
}
以上我们只是检验了可行性问题,但是题目中还有另外一个要求:操作次数最少。
因为在物品组合中没有先后顺序,所以我们可以通过物品组合中的物品数量来确定操作次数。
只有新的操作次数小于旧的操作次数的时候,我们才进行更新。
for (int i = 1; i <= n; i++) {//尝试每一个物品for (int j = 0; j < n; j++) {//尝试新的重量组合if (j - items[i] >= 0 && ans[i - 1][j] && ans[i - 1][j - items[i]])ans[i][j] = min(ans[i - 1][j], ans[i - 1][j - items[i]] + 1);else if (ans[i - 1][j])ans[i][j] = ans[i - 1][j];else if (j - items[i] >= 0 && ans[i - 1][j - items[i]])ans[i][j] = ans[i - 1][j - items[i]];}
}
注:1)以上代码段中,ans中元素的含义发生了变化:可行/不可行 -> 物品数量;
2)为了与不存在的组合(ans[i][j] = 0)相区分,我们为所有存在的组合物品数量添加偏置bias,也就是说,物品数量 = ans[i][j] - bias。
以上代码的空间复杂度、时间复杂度均可以接受,可以AC,接下来是优化部分qwq。
因为嫌弃这个算法的空间复杂度,所以我们对其进行优化,压缩到二维数组:
for (int i = 1; i <= n; i++) {//尝试每一个物品for (int j = 0; j < n; j++) {//尝试新的重量组合if (j - items[i] >= 0 && ans[(i - 1) % 2][j] && ans[(i - 1) % 2][j - items[i]])ans[i % 2][j] = min(ans[(i - 1) % 2][j], ans[(i - 1) % 2][j - items[i]] + 1);else if (ans[(i - 1) % 2][j])ans[i % 2][j] = ans[(i - 1) % 2][j];else if (j - items[i] >= 0 && ans[(i - 1) % 2][j - items[i]])ans[i % 2][j] = ans[(i - 1) % 2][j - items[i]];}
}
还是嫌弃?继续压,压缩到一维数组:
for (int i = 1; i <= n; i++) {//尝试每一个物品for (int j = n; j >= items[i]; j--) {//尝试新的重量组合if (j - items[i] >= 0 && ans[j] && ans[j - items[i]])ans[j] = min(ans[j], ans[j - items[i]] + 1);else if (ans[j]) ans[j] = ans[j];else if (j - items[i] >= 0 && ans[j - items[i]])ans[j] = ans[j - items[i]] + 1;}
}
然后我们删除一些无用的部分:
for (int i = 1; i <= n; i++) {//尝试每一个物品for (int j = n; j >= items[i]; j--) {//尝试新的重量组合if (ans[j] && ans[j - items[i]]) ans[j] = min(ans[j], ans[j - items[i]] + 1);else if (ans[j - items[i]]) ans[j] = ans[j - items[i]] + 1;}
}
嗯,好看多了qwq。
最后,AC代码如下:
#include <iostream>
using namespace std;
const int max_n = 3000;int ans[max_n + 1], n;
int items[max_n + 1];int main() {cin >> n;int fa;for (int i = 1; i < n; i++) {cin >> fa;items[fa]++;}int bias = 1;ans[0] = bias;for (int i = 1; i <= n; i++) {//尝试每一个物品for (int j = n; j >= items[i]; j--) {//尝试新的重量组合if (ans[j] && ans[j - items[i]]) ans[j] = min(ans[j], ans[j - items[i]] + 1);else if (ans[j - items[i]]) ans[j] = ans[j - items[i]] + 1;}}cout << 0;for (int i = 2; i <= n; i++) {cout << ' ' << ans[i - 1] - bias;}return 0;
}相关文章:
)
[Daimayuan] 树(C++,动态规划,01背包方案数)
有一棵 n n n 个节点的以 1 1 1 号点为根的有根树。现在可以对这棵树进行若干次操作,每一次操作可以选择树上的一个点然后删掉连接这个点和它的儿子的所有边。 现在我们想知道对于每一个 k k k ( 1 ≤ k ≤ n 1≤k≤n 1≤k≤n),最少需要多少次操作能…...

如何选择源代码加密软件
(SDC沙盒)和DLP、文档加密、云桌面等,其优缺点做客观比较如下: 比较内容安全容器(SDC沙盒)DLP文档加密云桌面代表厂家*信达卖咖啡、赛门贴科亿*通、IP噶德、*盾、*途四杰、深*服设计理念以隔离容器加准入技术为基础,构…...

TO-B类软件产品差异化
产品差异化,是在市场众多同质化产品中,突出自身产品亮点的重要方式。对于客户来讲其选择是多种多样的,与其花费大量的时间研究每一家产品的特点,还不如直接选择品牌更大、价格更低的产品来的直接,因此显而易见的突出产…...
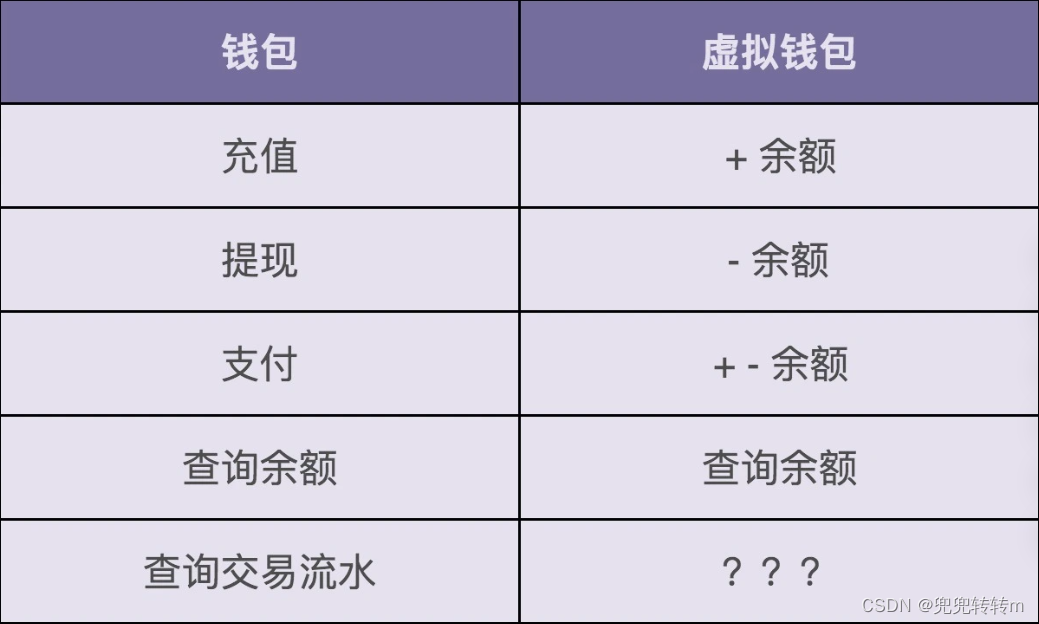
设计模式之美-实战一(上):业务开发常用的基于贫血模型的MVC架构违背OOP吗?
领域驱动设计(Domain Driven Design,简称DDD)盛行之后,这种基于贫血模型的传统的开发模式就更加被人诟病。而基于充血模型的DDD开发模式越来越被人提倡。所以,我打算用两节课的时间,结合一个虚拟钱包系统的…...

ChatGPT如何训练自己的模型
ChatGPT是一种自然语言处理模型,它的任务是生成自然流畅的对话。如果想要训练自己的ChatGPT模型,需要进行大量的数据收集、预处理、配置训练环境、模型训练、模型评估等过程。本文将详细介绍这些过程,帮助读者了解如何训练一个高品质的ChatGP…...
)
springboot使用线程池的实际应用(一)
在实际Spring Boot项目中,我们可以使用Java的原生多线程或者使用Spring自带的线程池进行多线程编程。多线程的好处在于能够提高应用程序的运行效率,特别是在某些计算密集型场景下。以下是一些使用多线程的典型场景: 并发处理请求:…...

ESP-8266学习笔记
1、学习地址 【XMF09F系列资源】基于MicroPython的ESP8266物联网应用开发-赛教资源目录汇总-小蜜蜂笔记 Quick reference for the ESP8266 — MicroPython latest documentation 2、MicroPython及相关开发资源 3、固件烧录与uPyLoader的使用 烧录教程参考: https://www.…...

Java泛型简单的使用
前言 Java里面的泛型在实际开发中运用的很多,学过C的同学一定知道C的模板,而Java中的泛型,一定程度上和它还是挺像的。 相信写Java的人,大都有用过List的实现类ArrayList。在Java没有泛型之前,它的内部是一个Object的…...
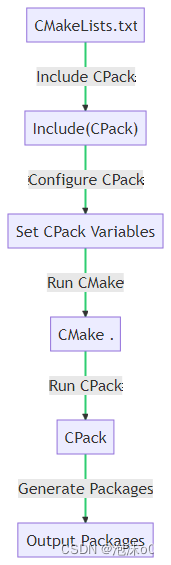
深度探索:Qt CMake工程编译后的自动打包策略
深度探索:Qt CMake工程编译后的自动打包策略 1. 引言(Introduction)1.1 Qt和CMake的基本概念(Basic Concepts of Qt and CMake)1.2 自动打包的重要性(Importance of Automatic Packaging) 2. Qt…...
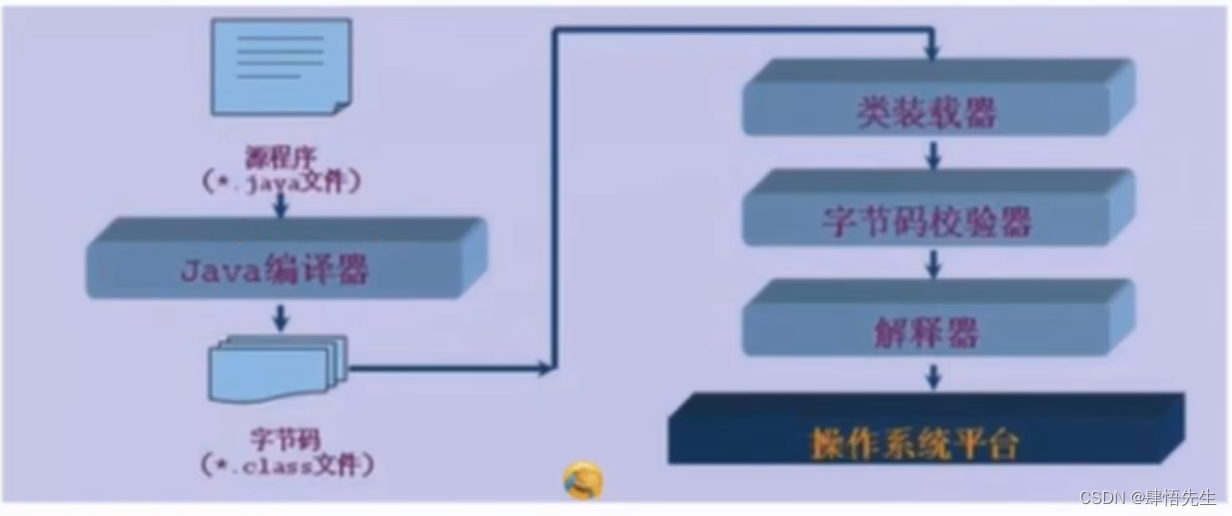
2.7 编译型和解释型
2.7 编译型和解释型 前面我们使用java和javac命令把Hello,World!在控制台输出。那为什么输出,这里我们需要掌握两个知识点。编译型语言和解释型语言。在计算机的高级编程语言就分为编译型语言和解释型语言。而我们的Java既有编译型的特点也有…...

校园网自动登陆(河南科技学院)
1. 介绍 河南科技学院校园网自动登陆(新乡的很多系统相似,可能也可以用?),java版。可以实现电脑,路由器,软路由的自动认证wifi,后续会上传docker版本的。 源码地址 github:https://…...

C++11 override和final关键字
C11中的override和final关键字是为了增强代码的编译时类型检查和面向对象设计中的继承机制。 override关键字用于显示地表明派生类中的成员函数覆盖了基类中的虚函数。当派生类中的函数与基类中的虚函数签名不同或者没有使用override关键字时,编译器会给出警告或错…...

kafka的log存储解析
kafka的log存储解析——topic的分区partition分段segment以及索引等 引言Kafka中的Message是以topic为基本单位组织的,不同的topic之间是相互独立的。每个topic又可以分成几个不同的partition(每个topic有几个partition是在创建topic时指定 的),每个…...
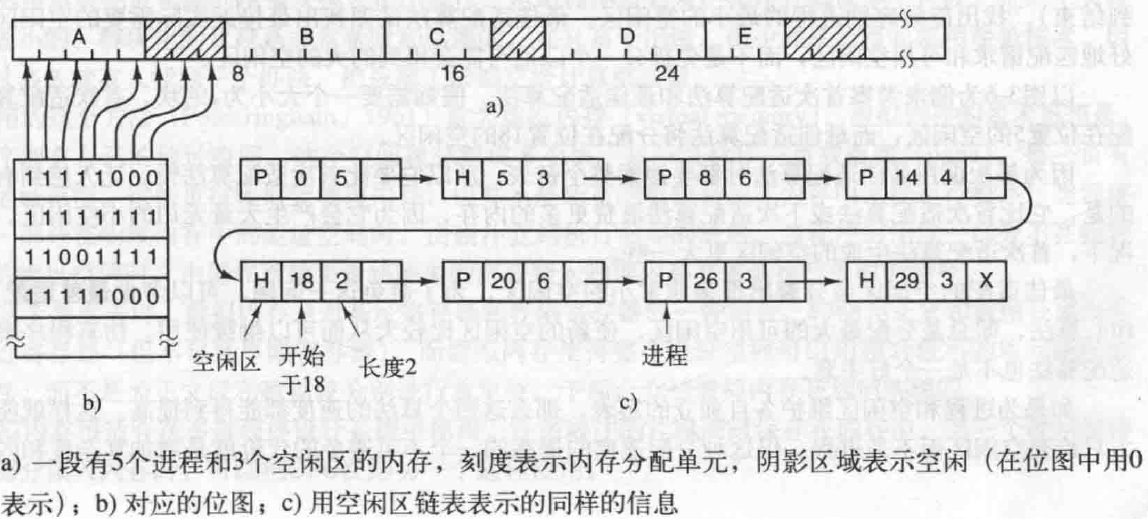
4.文件系统
组成 Linux:一切皆文件 索引节点(I-node) I-node(Index Node):文件系统的内部数据结构,用于管理文件的元数据和数据块。 文件的元数据:包括文件的权限、拥有者、大小、时间戳、索引…...

Shell脚本case in esac分支语句应用
记录:434 场景:Shell脚本case in esac分支语句应用。 版本:CentOS Linux release 7.9.2009。 1.case in esac格式 格式: case 值 in 模式1)expression;; 模式2)expression;; 模式n)expression;; esac 解析:case…...
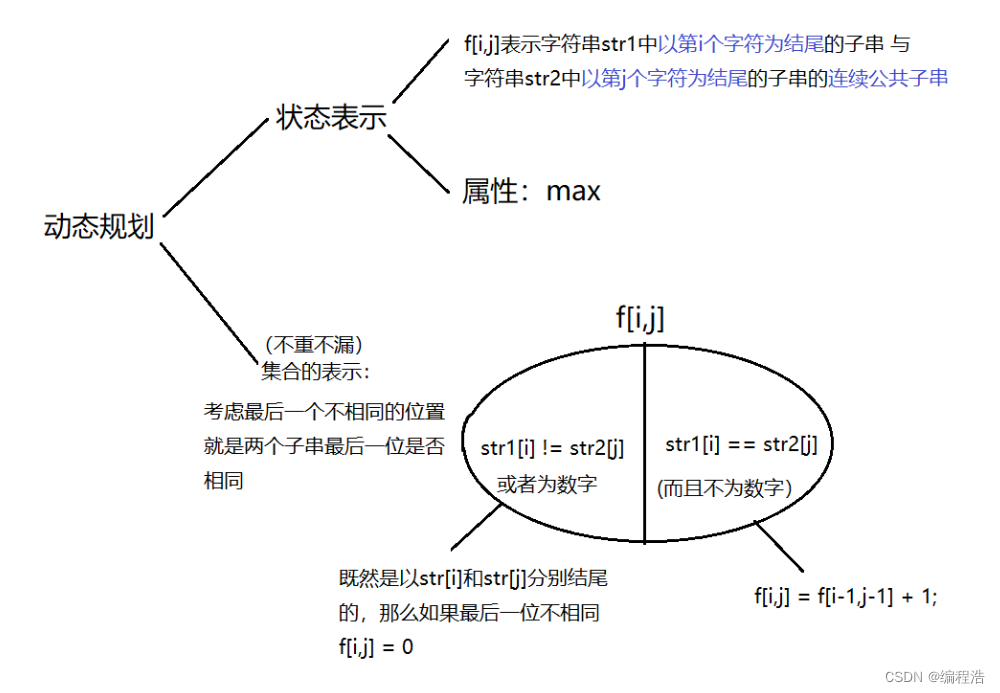
【线性dp必学四道题】线性dp四道经典例题【最长上升子序列】、【最长公共子序列】、【最长公共上升子序列(maxv的由来)】【最长公共子串】
【最长上升子序列】、【最长公共子序列】、【最长公共上升子序列】 最长上升子序列f[i] 表示以i结尾的最长子序列 最长公共子序列f[i][j] 表示 a前i 和 b前j个 最长公共长度 最长公共上升子序列f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合 最长公共子…...

追寻幸福:探索幸福的关键特征和行为
目录 1. 积极的心态 2. 良好的人际关系 3. 自我接纳和自尊 4. 追求意义和目标 5. 健康的身心状态 6. 感知和实现个人价值 幸福是一个主观的感受,因此不同的人对于幸福的定义和追求方式可能会有所不同。然而,有一些共同的特点和行为模式,…...

Redis-02-集群
一、redis5搭建集群 1.1、案例:搭建6台redis主机,配置如下 redis并发量:https://www.gxlcms.com/redis-350423.html主机IP:192.168.168.60~65修改redis配置文件hash槽移动,槽内的数据也随之移动 [root60 ~]# vim /e…...
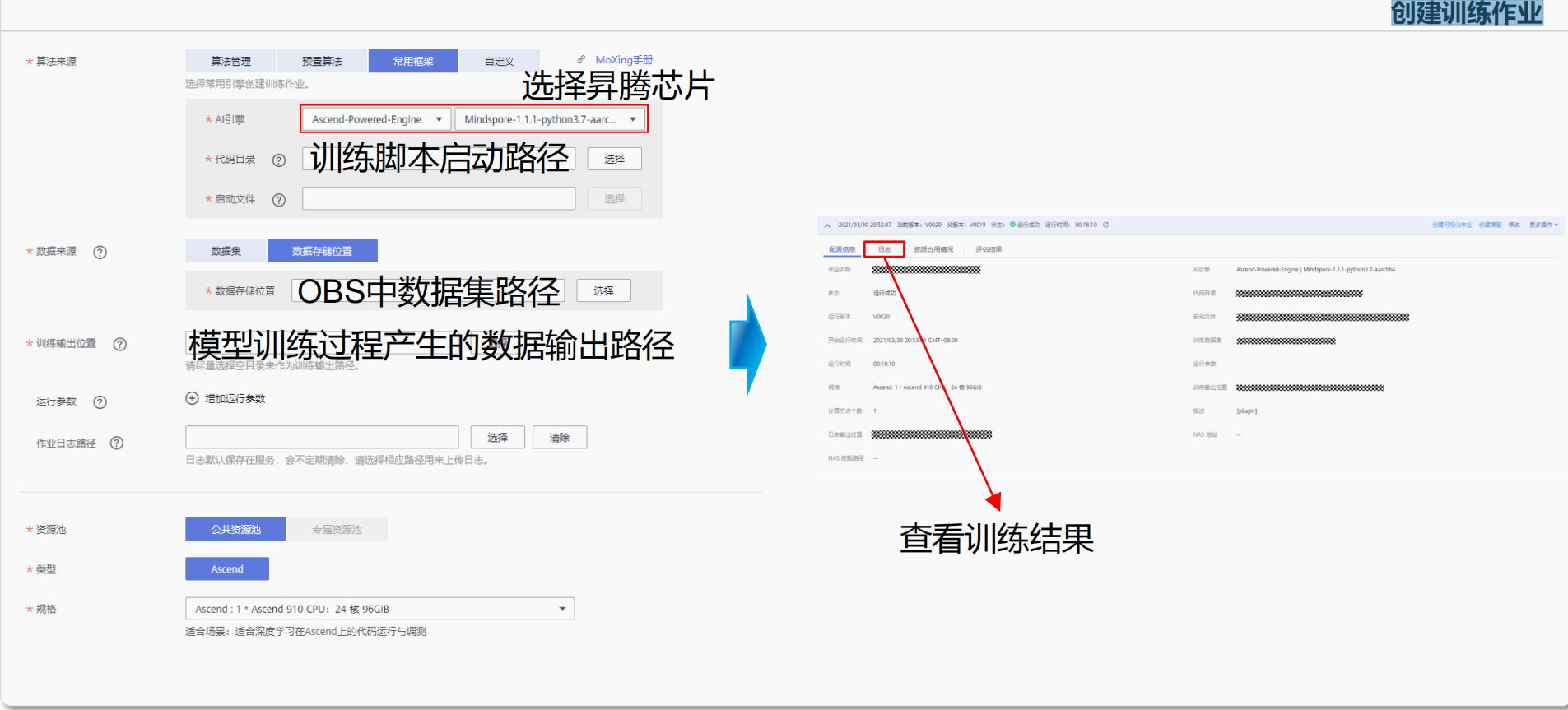
【2023 · CANN训练营第一季】MindSpore模型快速调优攻略 第三章——MindSpore云上调试调优
1.ModelArts云上调试调优 ModelArts密钥初始化 详细教程: 初始化OBS服务 创建训练作业 2.MindSpore IDE插件效率提升 通过智能代码块推荐、代码自动补全等特性,提升MindSpore脚本开发效率,对接ModelArts云服务,实现模型训…...
python笔记17_实例演练_二手车折旧分析p2
…… 书接上文 4.车辆等级维度 探查车龄为5年的车辆,折旧价值与车辆等级的关系。 # 筛选出车龄为5的数据创建新表 data_age5 data[data[age] 5] data_age5 # 分组聚合计算均值 data_car_level data_age5.groupby(car_level_name)[lowest_price].mean().reset…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
