从零学算法
198.你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
- 我的原始人解法:首先试一下分成一个个子问题,很容易想到的是,偷到 1 号房屋为止的最高金额,偷到 2 号房屋为止的最高金额…, 那么就有 f[i] 为偷到最后一个房屋为 i 时的最高金额(不一定就偷了 i 房屋,只是范围到 i 为止),接着找关联性,注意限制条件不能偷连续的房屋,首先 f[0] ,只能偷房屋 1,就直接为 nums[0] ,接着 f[1] 开始有说法了,两个房屋,我要么偷了前一个,这个不偷了,要么前一个没偷,我偷这个,两者我取最大值,所以为 max(f[0],nums[1]), f[2] ,同理 f[2] 也是两种可能,如果我偷了前一个房屋,那么我这个房屋是肯定不能偷了,也就是说我只能是 f[2-1],而如果我前一天没偷,那么我今天必偷无疑,也就是 f[2-2] + nums[2],两者之中我取最大的可能性即可,以此类推,这也就得到了状态转移方程和初始值。为了方便我定义数组时长度加了 1,表示第一天的时候,前一天(逻辑上不存在,所以正好为 0)不偷的金额为 0,偷则为 nums[0]。
-
public int rob(int[] nums) {int m = nums.length;int[] f = new int[m+1];f[1] = nums[0];for(int i=2; i<=m; i++){f[i] = Math.max(f[i-1],f[i-2]+nums[i-1]);}return f[m];} - 由于我们只需要知道前一天偷或不偷,所以定义两个变量滚动更新记录就足够了,不需要数组
-
int m = nums.length;int x1=0,x2=nums[0];for(int i=2; i<=m; i++){int temp = Math.max(x2,x1+nums[i-1]);x1 = x2;x2 = temp;}return Math.max(x1,x2); - 他人题解我就不看了
相关文章:

从零学算法
198.你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定一个代表每个房屋存放金额…...
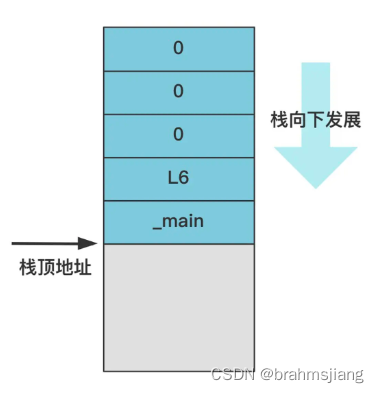
《Linux0.11源码解读》理解(四) head之重新设置IDT/GDT
上节提到,现在cs:ip指向0地址,此处存储着作为操作系统核心代码的system模块,是由head.s和 main.c以及后面所有源代码文件编译链接而成。head.s(以下简称head)紧挨着main.c,我们先执行head。 重新设置内核栈 _pg_dir: _startup_3…...
精心整理版(4)》)
<SQL>《SQL命令(含例句)精心整理版(4)》
《SQL命令(含例句)精心整理版(4)》 14 数据库对象14.1 表14.2 视图14.3 存储过程14.3.1 概念14.3.2 创建存储过程14.3.2 调用存储过程14.3.3 DbVisualizer工具中调用方法14.3.3 DB2命令行脚本调用方法14.3.4 DB2中两个存储过程报错…...

C++死锁
死锁是指两个或两个以上的线程在执行过程中,由于竞争资源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推进下去。此时称系统处于死锁状态或系统产生了死锁,这些永远在互相等待的状态称为死锁。 死锁通常发生…...

[自学记录02|百人计划]纹理压缩
一、什么是纹理压缩 纹理压缩是为了解决内存、带宽问题,专为在计算机图形渲染系统中存储纹理而使用的图像压缩技术。 1.图片格式和纹理格式的区别 (1)图片格式 图片格式是图片文件的存储格式,通常在磁盘、内存中储存和传输文件时使用;例如…...

C++泛型编程之模板
目录 一、什么是泛型编程 二、函数模板 2.1函数模板的概念 2.2函数模板格式 2.3函数模板的原理 2.5函数模板的实例化 2.6模板参数的匹配原则 三、类模板 3.1类模板的定义格式 3.2 类模板的实例化 四、非类型模板参数 五、模板的特化 5.1模板特化的概念:…...
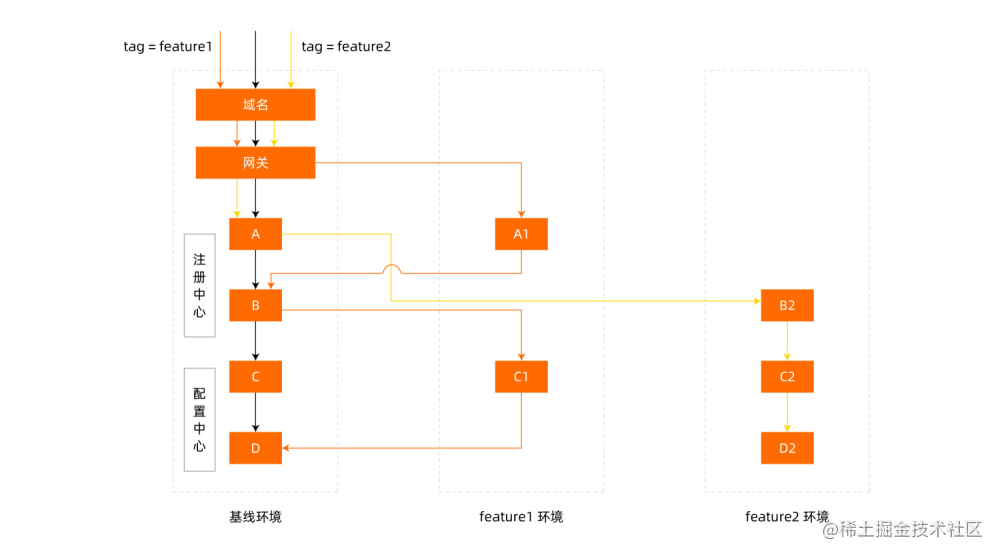
极氪汽车 APP 系统云原生架构转型实践
作者:极氪汽车 前言 新能源汽车已经成为我国汽车市场再次崛起的关键支柱,随着新能源汽车市场的快速发展,不同类型的品牌造车厂商呈现出百花齐放的态势。极氪汽车是吉利控股集团旗下高端纯电汽车新品牌,2021 年 4 月极氪发布首款…...
)
一个UDP下载服务器的实现(模拟下载文件)
本期分享的主要是使用UDP实现文件下载功能,需要自己编写服务器和客户端,实现的功能主要有以下几个: (1)服务器可以为请求的用户下发文件数据(前提是服务器得有这个数据文件) (2&…...

01.hadoop上课笔记之hadoop介绍
1.大数据介绍 可以对未来数据预测 google通过搜索预测流感,足球球员有一 定关联…caict可以得到数据hbase hive林子雨mooc数据要进行挖掘(推断更多信息) 2.大数据是非结构化数据多:声音,图片… 3.大数据影响因素 大多快低 tb pb eb zb 1.硬件 2.网络带宽 4.大数据的特征 数据量…...

小鹏汽车Q1财报:押注G6、大力降本,明年智驾BOM降半
作者 | 德新编辑 | 王博 小鹏汽车本周发了Q1财报,数据不好看,以致于在微博端也发了公开信。 那后续呢? 小鹏第二季度指引是,总交付数量约为2.1 - 2.2万辆,收入预计约为45 - 47亿元;四季度,…...
VMware ESXi 8.0U1a 发布 - 领先的裸机 Hypervisor
VMware ESXi 8.0U1a 发布 - 领先的裸机 Hypervisor 请访问原文链接:https://sysin.org/blog/vmware-esxi-8-u1/,查看最新版。原创作品,转载请保留出处。 作者主页:sysin.org 2023-06-01, VMware vSphere 8.0U1a 发布。 详见&am…...

Unity的IPreprocessBuild:深入解析与实用案例
Unity IPreprocessBuild Unity IPreprocessBuild是Unity引擎中的一个非常有用的功能,它可以让开发者在构建项目时自动执行一些操作。这个功能可以帮助开发者提高工作效率,减少手动操作的时间和错误率。在本文中我们将介绍Unity IPreprocessBuild的使用方…...

htmlCSS-----CSS选择器(下)
目录 前言: 2.高级选择器 (1)子代选择器 (2)伪类选择器 (3)后代选择器 (4)兄弟选择器 相邻兄弟选择器 通用兄弟选择器 (5)并集选择器 &am…...

RDK X3 Module发布,全新软硬件平台加速实现量产级产品落地
机器人开发是一段美妙的旅程。GEEKROS创始人杨状状是地平线社区的一名开发者,热衷于鼓捣各类机器人,2022年,状状第一时间就拿到了地平线旭日X3派(简称旭日X3派),基于TogetheROS™.Bot机器人操作系统&#x…...

【面试实战】Redis缓存设计
文章目录 Redis缓存出现的问题🙎♂️面试官:什么是缓存雪崩?🙎♂️面试官:怎样解决缓存雪崩?🙎♂️面试官:什么是缓存击穿?🙎♂️面试官:怎样解决缓存击穿?🙎♂️面试官:什么是缓存穿透?🙎♂️面试官:怎样解决缓存穿透?🙎♂️面试官:…...

如何解决js定时器不准确问题
为什么会出现定时器不准确呢? 这个其实就得提到js执行机制了,叫做事件循环Eventloop 循环机制中,异步事件 setInterval 到时后会把回调函数放入消息队列中Event Queue,主线程的宏任务执行完毕后依次执行消息队列的微任务ÿ…...
学习笔记——vue中使用el-dropdown组件报错
今天在工作中,发现使用el-select做的下拉框,下拉菜单展开后,鼠标点击下拉框之外的区域时,下拉菜单没有收起。然后,我打开控制台,发现了这个错误。 Uncaught TypeError: Cannot read properties of null (re…...
)
Java之旅(八)
Java 条件运算符 Java 条件运算符用于根据一个条件表达式的布尔值来决定程序执行的流程。条件运算符有三种类型:if、else 和 switch。 if 语句的一般格式如下: if (condition) {// 条件为 true 执行的代码块 } 其中,condition 是一个 bool…...
,四则运算(100%通过+复盘思路))
华为OD机试真题(Java),四则运算(100%通过+复盘思路)
一、题目描述 输入一个表达式(用字符串表示),求这个表达式的值。 保证字符串中的有效字符包括[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’, ‘)’,‘[’, ‘]’,‘{’ ,‘}’。且表达式一定合法。 数据范围:表达式计算结果和过程中满足∣val∣≤1000 ,字符串长度满…...
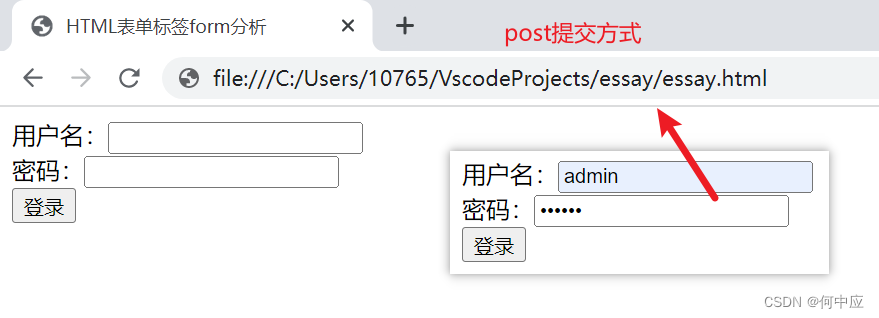
HTML表单标签form分析
说明:在html的标签中,表单标签与后台联系密切,像用户登录、注册,都是用到页面的表单标签,用户将信息填入到表单中,提交到后端业务中校验处理,再将结果反馈给前端页面。 表单内的标签分别有&…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...
