设置线程池的大小
线程池的理想大小取决于被提交任务的类型以及所部署系统的特性。在代码中通常不会固定线程池的大小,而应该通过某种配置机制来提供,或者根据Runtime. availableProcessors来动态计算。
幸运的是,要设置线程池的大小也并不困难,只需要避免“过大”和“过小”这两种极端情况。如果线程池过大,那么大量的线程将在相对很少的CPU和内存资源上发生竞争,这不仅会导致更高的内存使用量,而且还可能耗尽资源。如果线程池过小,那么将导致许多空闲的处理器无法执行工作,从而降低吞吐率。
要想正确地设置线程池的大小,必须分析计算环境、资源预算和任务的特性。在部署的系统中有多少个CPU?多大的内存?任务是计算密集型、I/O密集型还是二者皆可?它们是否需要像JDBC连接这样的稀缺资源?如果需要执行不同类别的任务,并且它们之间的行为相差很大,那么应该考虑使用多个线程池,从而使每个线程池可以根据各自的工作负载来调整。
对于计算密集型的任务,在拥有Nopu个处理器的系统上,当线程池的大小为 时,通常能实现最优的利用率。(即使当计算密集型的线程偶尔由于页缺失故障或者其他原因而暂停时,这个“额外”的线程也能确保CPU的时钟周期不会被浪费。)对于包含I/O操作或者其他阻塞操作的任务,由于线程并不会一直执行,因此线程池的规模应该更大。要正确地设置线程池的大小,你必须估算出任务的等待时间与计算时间的比值。这种估算不需要很精确,并且可以通过一些分析或监控工具来获得。你还可以通过另一种方法来调节线程池的大小:在某个基准负载下,分别设置不同大小的线程池来运行应用程序,并观察CPU利用率的水平。
给定下列定义:
Uspu=target CPU utilization,O≤Uepu≤1
W/C =ratio of wait time to compute time
要使处理器达到期望的使用率,线程池的最优大小等于:
可以通过Runtime 来获得CPU的数目:
int N_CPUS= Runtime.getRuntime( ).availableProcessors( );
当然,CPU周期并不是唯一影响线程池大小的资源,还包括内存、文件句柄、套接字句柄和数据库连接等。计算这些资源对线程池的约束条件是更容易的:计算每个任务对该资源的需求量,然后用该资源的可用总量除以每个任务的需求量,所得结果就是线程池大小的上限。
当任务需要某种通过资源池来管理的资源时,例如数据库连接,那么线程池和资源池的大小将会相互影响。如果每个任务都需要一个数据库连接,那么连接池的大小就限制了线程池的大小。同样,当线程池中的任务是数据库连接的唯一使用者时,那么线程池的大小又将限制连接池的大小。
相关文章:

设置线程池的大小
线程池的理想大小取决于被提交任务的类型以及所部署系统的特性。在代码中通常不会固定线程池的大小,而应该通过某种配置机制来提供,或者根据Runtime. availableProcessors来动态计算。 幸运的是,要设置线程池的大小也并不困难,只需要避免“过大”和“过…...

Vue3 除了 keep-alive,还有哪些实现页面缓存的方法
有这么一个需求:列表页进入详情页后,切换回列表页,需要对列表页进行缓存,如果从首页进入列表页,就要重新加载列表页。 对于这个需求,我的第一个想法就是使用keep-alive来缓存列表页,列表和详情…...

JavaScript闭包
定义 定义:在计算机科学中,闭包(Closure)是一个函数及其相关引用环境组合而成的实体。简单来说,闭包是指一个函数以及该函数访问的外部变量的集合。在一些编程语言中,函数可以访问在其定义时所处的上下文中…...

华为OD机试之不含101的整数(Java源码)
不含101的数 题目描述 小明在学习二进制时,发现了一类不含 101的数,也就是: 将数字用二进制表示,不能出现 101 。 现在给定一个整数区间 [l,r] ,请问这个区间包含了多少个二进制不含 101 的整数? 输入描述…...
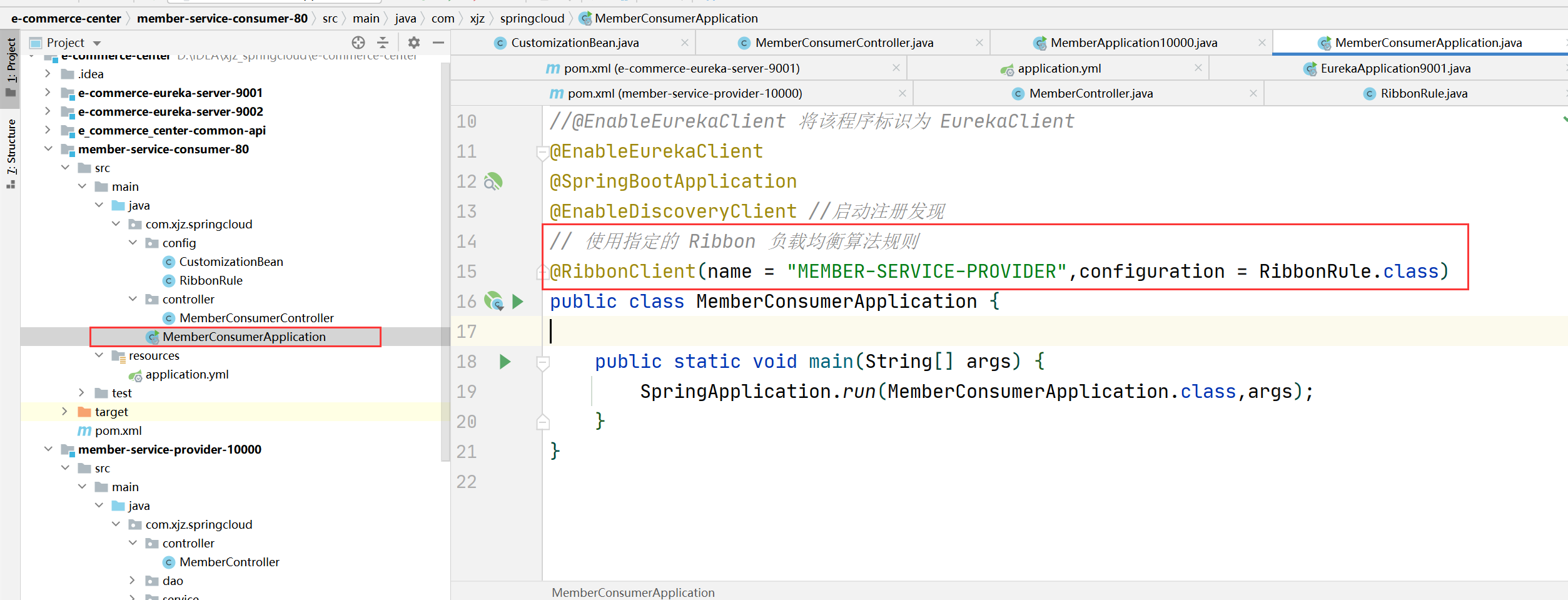
SpringCloud Ribbon 学习
SpringCloud Ribbon 学习 文章目录 SpringCloud Ribbon 学习1. Ribbon 是什么?2. LB(Load Balance)3 Ribbon 架构图&机制4 Ribbon 常见负载均衡算法5 测试 1. Ribbon 是什么? Spring Cloud Ribbon 是基于 Netflix Ribbon 实现的一套客户端 负载均衡…...

预告:XuperOS Global 国际化进展
XuperOS新年致辞中,我们提到XuperOS成长计划的最后一个阶段是国际化。伴随前三个阶段创世、监督、共建先后落地,很多用户特来咨询XuperOS国际化进展,我们在此统一说明。 按照之前的规划,XuperOS将在海外部署一条新的开放链XuperOS…...

炫技操作--递归实现翻转链表(java)
递归实现链表的逆序 leetcode 206题。 翻转链表递归解法普通方式实现链表翻转链表专题 leetcode 206题。 翻转链表 leetcode链接用于测试 题目:描述 将一个链表翻转: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 递归解法 解题思路…...

华为OD机试真题 Java 实现【求最小公倍数】【牛客练习题】
一、题目描述 正整数A和正整数B 的最小公倍数是指 能被A和B整除的最小的正整数值,设计一个算法,求输入A和B的最小公倍数。 数据范围:1≤a,b≤100000 。 二、输入描述 输入两个正整数A和B。 三、输出描述 输出A和B的最小公倍数。 四、解…...

[java]两数之和 II - 输入有序数组
两数之和 II - 输入有序数组 leetcode 167 原题链接解题思路解题代码排序专题 leetcode 167 原题链接 167. 两数之和 II - 输入有序数组 – 原题链接 题目描述: 给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出…...

Linux-0.11 boot目录head.s详解
Linux-0.11 boot目录head.s详解 模块简介 在head.s中,操作系统主要做了如下几件事: 重新设置中断描述符和全局描述符检查A20地址线是否开启检查数学协处理器初始化页表并开启分页跳转到main函数执行 过程详解 重新设置IDT和GDT 在setup.s中我们已经…...
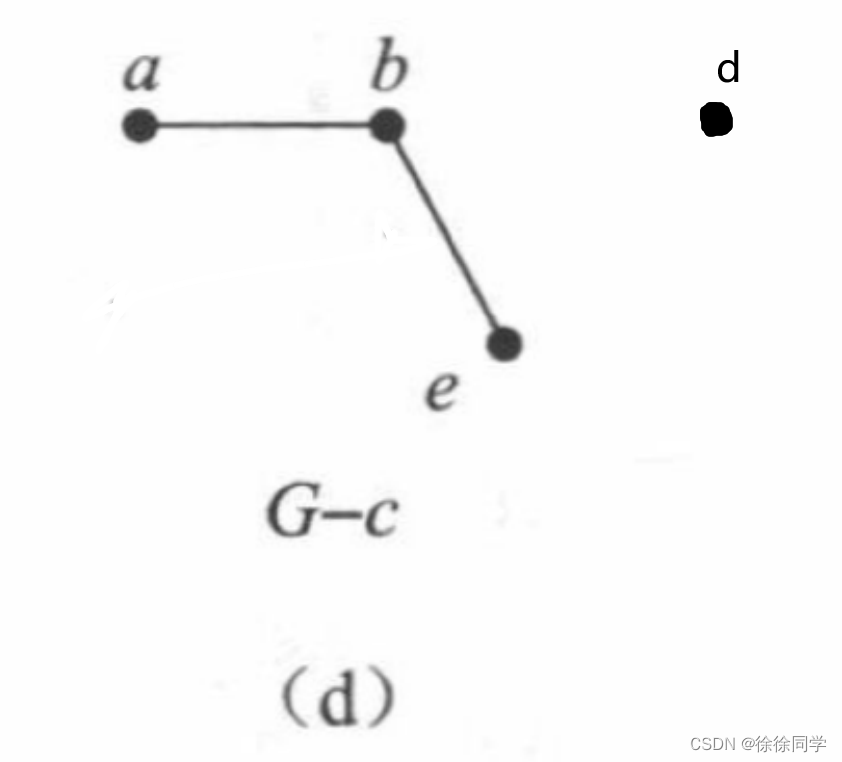
离散数学_十章-图 ( 3 ):由旧图构造新图
📷10.3 由旧图构造新图 概念1. 子图2. 真子图3. 导出的子图 旧图构造新图的方法1. 删除或增加图中的边2. 边的收缩3. 删除顶点 有时解决问题只需要图的一部分。 比如我们现在只关心大型计算机网络中涉及济南,广州,深圳的计算机中心࿰…...

Golang每日一练(leetDay0083) 汇总区间、多数元素II
目录 228. 汇总区间 Summary Ranges 🌟 229. 多数元素 II Majority Element ii 🌟🌟 🌟 每日一练刷题专栏 🌟 Rust每日一练 专栏 Golang每日一练 专栏 Python每日一练 专栏 C/C每日一练 专栏 Java每日一练 专…...
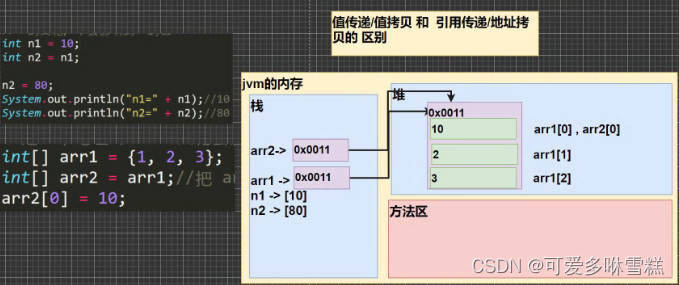
JAVA数组基础
目录 一、使用方式 1-动态初始化 ①先声明数组 ② 创建数组 ③分配方式 二、使用方式 2-静态初始化(直接在声明的同时初始化{ } ) 三、数组使用注意事项和细节 四、数组两种初始化方式都是将内存空间分配到堆上面的 一、使用方式 1-动态初始化 …...
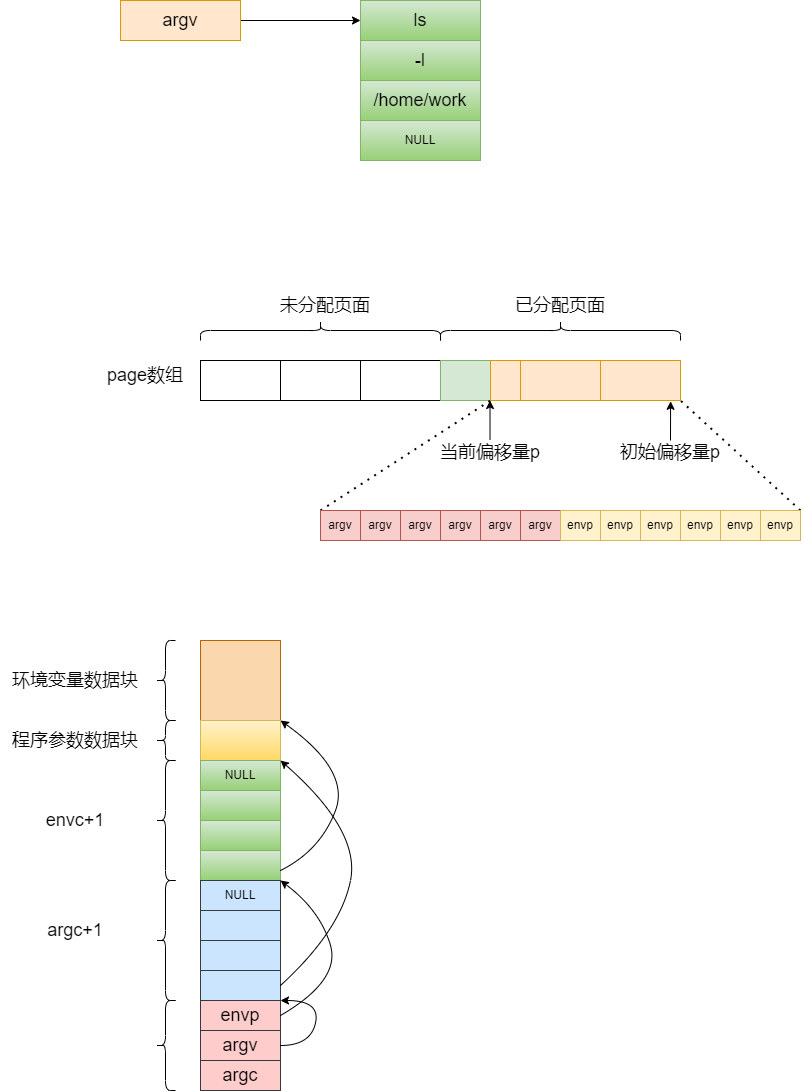
Linux-0.11 文件系统exec.c详解
Linux-0.11 文件系统exec.c详解 模块简介 该模块实现了二进制可执行文件和shell脚本文件的加载和执行。 函数详解 create_tables static unsigned long * create_tables(char * p,int argc,int envc)该函数的作用是建立参数和环境变量指针表。 create_table的作用就是建立…...
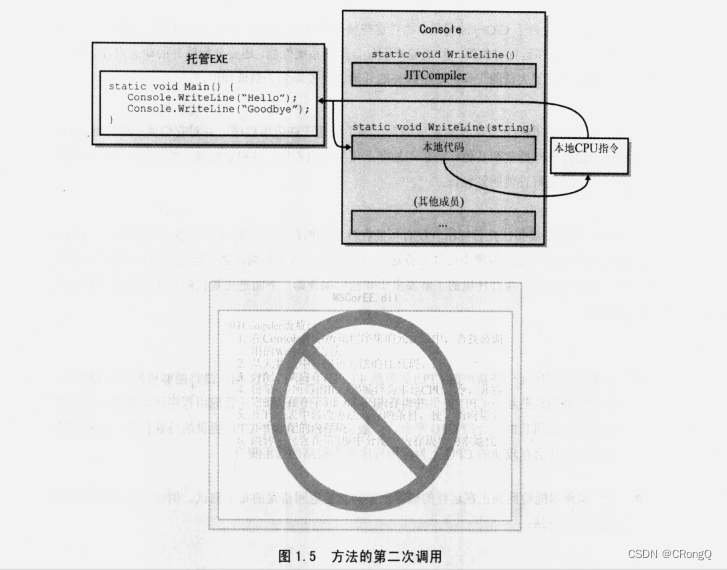
NET框架程序设计-第1章.NET框架开发平台体系架构
1.1 .NET 框架基本组成 .NET 框架的核心便是通用语言运行时(Commomn Language Runtime,简称 CLR),CLR 是一个可被各种不同的编程语言所使用的运行时。 托管模块(mangaed module): 一个需要 CLR 才能执行的标准 Window…...
(哈希表 ) 349. 两个数组的交集 ——【Leetcode每日一题】
❓349. 两个数组的交集 难度:简单 给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。 示例 1: 输入:nums1 [1,2,2,1], nums2 [2,2] 输出:[…...
)
JavaScript基本语法(二)
JavaScript基本语法 1、变量1.1、简介1.2、变量命名规则1.3、JS的关键字和保留字1.4、声明提升 2、JavaScript数据类型2.1、基本类型2.2、引用类型2.3、两种类型的区别2.4、字符串常用方法 3、数据类型转换 1、变量 1.1、简介 在 JavaScript 中声明一个新变量的方法是使用关键…...

ChatGPT3.5-4资源汇总,直连无梯子
什么是ChatGPT? ChatGPT,全称:聊天生成预训练转换器(英语:Chat Generative Pre-trained Transformer),是OpenAI开发的人工智能聊天机器人程序,于2022年11月推出。该程序使用基于GPT-3.5、GPT-4…...
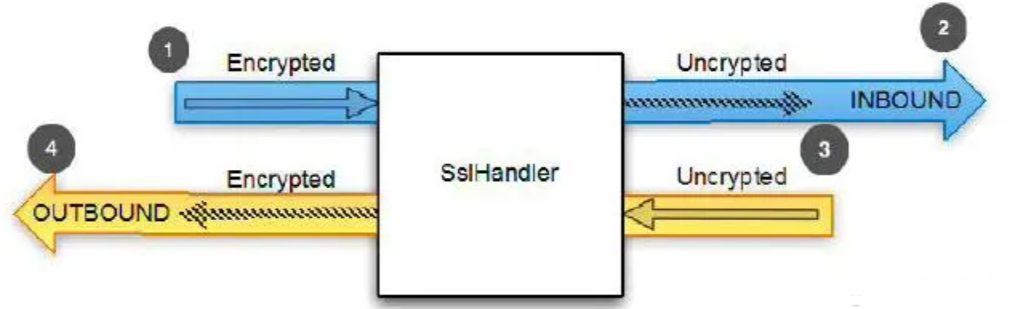
【Netty】使用 SSL/TLS 加密 Netty 程序(二十)
文章目录 前言一、SSL/TLS概述二、Sslhandler类 前言 回顾Netty系列文章: Netty 概述(一)Netty 架构设计(二)Netty Channel 概述(三)Netty ChannelHandler(四)ChannelP…...

runway gen2
来自Runway文生成视频ai大模型Gen-2_哔哩哔哩_bilibili来自Runway文生成视频ai大模型Gen-2,距离视频制作自由又近了一步。, 视频播放量 1651、弹幕量 0、点赞数 21、投硬币枚数 2、收藏人数 42、转发人数 22, 视频作者 旭升说, 作者简介 一起聊下互联网的那些事&…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...
