华为OD机试之最小调整顺序次数、特异性双端队列(Java源码)
最小调整顺序次数、特异性双端队列
题目描述
有一个特异性的双端队列,该队列可以从头部或尾部添加数据,但是只能从头部移出数据。
小A依次执行2n个指令往队列中添加数据和移出数据。其中n个指令是添加数据(可能从头部添加、也可能从尾部添加),依次添加1到n;n个指令是移出数据。
现在要求移除数据的顺序为1到n。
为了满足最后输出的要求,小A可以在任何时候调整队列中数据的顺序。
请问 小A 最少需要调整几次才能够满足移除数据的顺序正好是1到n;
输入描述
第一行一个数据n,表示数据的范围。
接下来的2n行,其中有n行为添加数据,指令为:另外 n 行为移出数据指令,指令为:"remove" 的形式,表示移出1个数据;
- "head add x" 表示从头部添加数据 x,
- "tail add x" 表示从尾部添加数据x,
1 ≤ n ≤ 3 * 10^5。
所有的数据均合法。
输出描述
一个整数,表示 小A 要调整的最小次数。
源码和解析
解析:
其实这个题只要理解了就其实还蛮简单的。小编当时做这个提题目时候前面一脸懵B,压根不知道在说个啥。就只知道要调整次数,但是不确定这个调整次数是啥。
head add 1
[1]
tail add 2
[1, 2]
remove
[2]
head add 3
[3, 2]
tail add 4
[3, 2, 4]
head add 5
[5, 3, 2, 4]
remove
排序了
[3, 4, 5]
remove
[4, 5]
remove
[5]
remove
[]
这个是用例中的例子 输出过程。 认真去体会每个指令执行后的结果
若输入变成
5
head add 2
tail add 1
remove
head add 3
tail add 4
head add 5
remove
remove
remove
remove
排序了1次
那么其输出过程为:
head add 2
[2]
tail add 1
[2, 1]
remove
排序了
[2]
head add 3
[3, 2]
tail add 4
[3, 2, 4]
head add 5
[5, 3, 2, 4]
remove
排序了
[3, 4, 5]
remove
[4, 5]
remove
[5]
remove
[]
排序了2次
====》可以推出 ,当集合中首位值不是集合中最小值是,需要进行调整。而一次调整包含了多次交换位置过程。可以简单的理解为1次排序过程。
示例代码:
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Scanner;public class T33 {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);String input = scanner.nextLine();int num = Integer.parseInt(input); // 数据范围 并非是数的个数List<Integer> numList = new ArrayList<Integer>();int count = 0;// 调整次数int removeNum = 1;// 下一次需要移走哪一个for (int i = 0; i < num * 2; i++) {input = scanner.nextLine();String strArr[] = input.split(" ");System.out.println(input);if (strArr[0].equals("remove")) {// remove 从头部移出数据if (numList.get(0) == removeNum) {numList.remove(0);removeNum++;} else {count++;// 调整次序 从小到大排序一下numList.sort(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {if (o1 > o2)return 1;if (o1 < o2)return -1;return 0;}});System.out.println("排序了");numList.remove(0);removeNum++;}}// 头部添加if (strArr[0].equals("head")) {numList.add(0, Integer.parseInt(strArr[2]));// continue;} else if (strArr[0].equals("tail")) {// 尾部添加numList.add(Integer.parseInt(strArr[2]));}System.out.println(numList);}System.out.println(count);}
}相关文章:
)
华为OD机试之最小调整顺序次数、特异性双端队列(Java源码)
最小调整顺序次数、特异性双端队列 题目描述 有一个特异性的双端队列,该队列可以从头部或尾部添加数据,但是只能从头部移出数据。 小A依次执行2n个指令往队列中添加数据和移出数据。其中n个指令是添加数据(可能从头部添加、也可能从尾部添加…...

2023年武汉住建厅七大员怎么报名?报名流程?精准题库一次过??
2023年武汉住建厅七大员怎么报名?报名流程?精准题库一次过?? 2023年武汉住建厅七大员是指施工员、质量员、资料员、材料员、机械员、标准员、劳务员,报的最多的可能就是施工员,质量员和资料员 报名流程: 1…...

Rust每日一练(Leetday0014) 组合总和II、缺失正数、接雨水
目录 40. 组合总和 II Combination Sum II 🌟🌟 41. 缺失的第一个正数 First Missing Positive 🌟🌟🌟 42. 接雨水 Trapping Rain Water 🌟🌟🌟 🌟 每日一练刷题…...
EnjoyVIID部署
1、下载 git clone https://gitee.com/tsingeye/EnjoyVIID.git 2、导入数据库 创建表enjoyviid 导入数据库(修改数据库文件里的编码) EnjoyVIID/sql/tsingeye-viid.sql 3、修改配置 vim EnjoyVIID/tsingeye-admin/src/main/resources/application-dev.yml 修改数据库连接、re…...

用Python解决爱因斯坦的数学问题
1 问题 有一条阶梯,若每步跨2阶,则剩最后一阶,若每步跨3阶,则最后剩2阶,若每步跨5阶,则最后剩4阶,若每步跨6阶,则最后剩5阶,只有每次跨7阶,最后才刚好不剩&am…...

ChatGPT提示词攻略之基本原则
下面是调用openai的completion接口的函数。但在本文中并不是重点。了解一下就好。 import openai import osfrom dotenv import load_dotenv, find_dotenv _ load_dotenv(find_dotenv())openai.api_key os.getenv(OPENAI_API_KEY)def get_completion(prompt, model"gp…...
抖音seo源码如何开发部署?
前言:抖音seo源码,抖音矩阵系统源码搭建,抖音矩阵同步分发。抖音seo源码部署是需要对接到这些正规接口再来做开发的,目前账号矩阵程序开发的功能,围绕一键管理多个账号,做到定时投放,关键词自动…...

Java中常见锁的分类及概念分析
基于线程对同一把锁的获取情况分类 可重入锁 同一个线程可以多次获取锁 每次获取锁,锁的计数器加1,每次释放锁锁的计数器减1 锁的计数器归零,锁完全释放 Java中提供的synchronized,ReentrantLock,ReentrantReadWriteL…...
)
ConcurrentLinkedQueue的源码解析(基于JDK1.8)
ConcurrentLinkedQueue的源码解析(基于JDK1.8) ConcurrentLinkedQueue是Java集合框架中的一种线程安全的队列,它是通过CAS(Compare and Swap)算法实现的并发队列。在并发场景下,ConcurrentLinkedQueue能够…...
低资源方面级情感分析研究综述
文章目录 前言1. 引言2. 问题定义、数据集和评价指标2.1 问题定义2.2 任务定义2.3 常用数据集 3. 方面级情感分析的方法3.1 **方面词抽取**3.1.1 基于无监督学习的方法3.1.1.1 基于规则的方面词抽取3.1.1.2 基于统计的方面词抽取 3.1.2 基于有监督浅层模型的方法3.1.3 基于有监…...
将 PDF 压缩到 1 MB 或更小的 5 个工具
鉴于工作和生活中PDF文件的频繁传输,压缩文件大小成为PDF文件必不可少的一步,尤其是对于包含大量高清图片的文件。压缩不仅使您的文件兼容发送,还有助于存储优化。这意味着您将获得更多数据空间,适用于本地设备和云端。 想要将 …...

CSMA/CD协议之计算最短帧长问题
文章目录 前言CSMA/CD协议计算最短帧长 前言 本篇博客主要论述了如何计算 CSMA/CD 协议下的网络帧长问题,从概念入手,结合例题进行详细的分析。 CSMA/CD协议 概念: ① 载波监听多点接入/碰撞检测 ② 半双工通信 ③ 先听后发、边听边发、冲…...

第三章:什么是分库分表
文章目录 背景什么是分库分表为什么要分库分表性能可用性什么时候考虑分库分表什么时候分库什么时候分表背景 一个系统当伴随着用户量的激增,业务数据的不断增加,数据库表中的数据越来越多,如果再去对我们数据库中的表进行curd操作的时候,就会造成一些性能上的瓶颈问题! …...
)
SpringMVC第六阶段:数据在域中的保存(02)
数据在域中的保存(02) 1、Map或Model或ModelMap形式保存数据在request域中 在四个域中,我们使用最频繁的域就是request对象。往request域对象中,保存数据,还在以下的几种形式。 我们可以在Controller的方法中&#x…...
Springboot +spring security,认证方式---HTTP基本认证的实现
一.简介 这篇文章来学习下security的认证方式其中的HTTP基本认证。 二.Spring Security的认证方式 2.1什么是认证 认证: 就是用来判断系统中是否存在某用户,并判断该用户的身份是否合法的过程,解决的其实是用户登录的问题。认证的存在,是…...
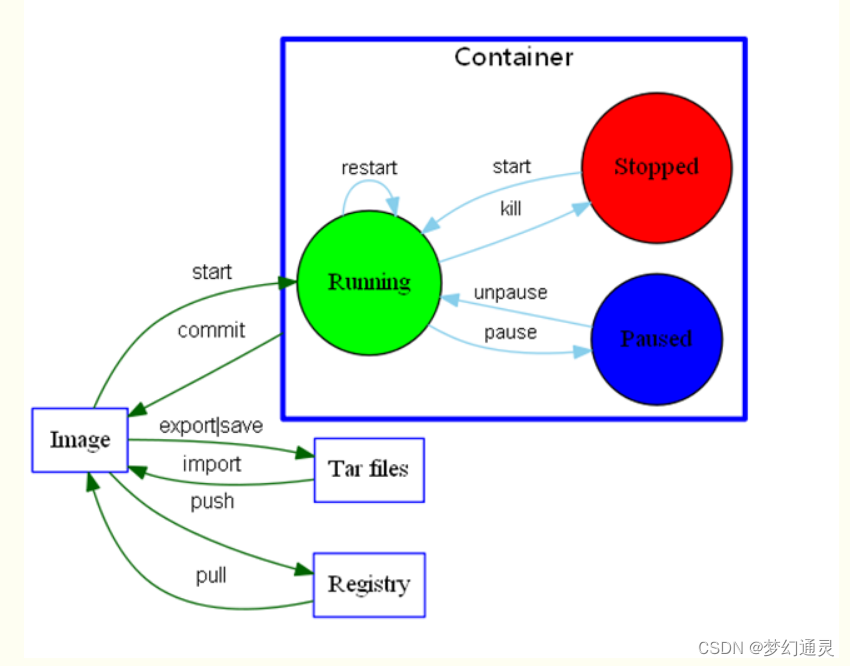
2023年系统分析师案例及论文(回忆版)
2023年5月27日,全国计算机等级上半年考试如期举行 北京市软件分析师考试地点在北京市对外贸易学校,早上外面下起雨,正如考前紧张的心情。 看考场分布图,44个考场,推测有44*301320名考生,本人所在的考场&am…...

数据结构与算法面试题
(1) 红黑树的了解(平衡树,二叉搜索树),使用 场景 把数据结构上几种树集中的讨论一下: 1.AVLtree 定义:最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一…...
C Primer Plus第十章编程练习答案
学完C语言之后,我就去阅读《C Primer Plus》这本经典的C语言书籍,对每一章的编程练习题都做了相关的解答,仅仅代表着我个人的解答思路,如有错误,请各位大佬帮忙点出! 1.修改程序清单10.7的rain.c程序&…...

奇舞周刊第493期:Hook 革命!浅谈 React 新 Hook 的未来与思想
关注前端生态发展,了解行业动向。 下面先一起看下本期周刊 摘要 吧~ 奇舞推荐 ■ ■ ■ Hook 革命!浅谈 React 新 Hook 的未来与思想 作者阳羡曾写文章对 React 新 Hook use 的设计理念和限制进行了深入分析,并提供了一个可能的实现来帮助读者…...
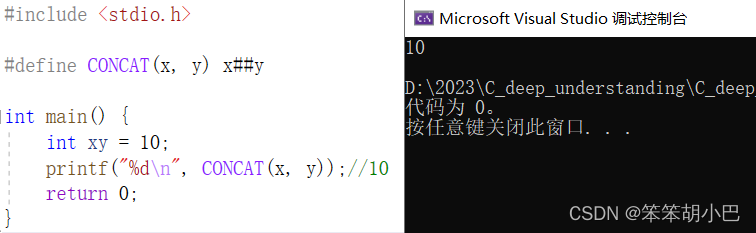
文件包含的本质、预处理符号、# vs ##
何为头文件? 在C语言中,文件包含是一种常见的编程技术,它允许程序员在一个源文件中使用另一个源文件中的函数或变量。 文件包含通常使用#include预处理指令来实现。#include指令告诉预处理器将文件的内容插入到当前文件的指定位置中。 例如&a…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
