CSMA/CD协议之计算最短帧长问题
文章目录
- 前言
- CSMA/CD协议
- 计算最短帧长
前言
本篇博客主要论述了如何计算 CSMA/CD 协议下的网络帧长问题,从概念入手,结合例题进行详细的分析。
CSMA/CD协议
概念:
① 载波监听多点接入/碰撞检测
② 半双工通信
③ 先听后发、边听边发、冲突停发、延迟重发
计算最短帧长
-
一个 CSMA/CD 基带总线网长度为 4000 4000 4000 m,信号传播速度为 2 ∗ 1 0 8 2*10^8 2∗108 m/s,假如位于总线两端的两台计算机在发送数据时发生了冲突,试问:
(1)两台计算机间的信号传播延迟是多少?往返传播时间是多少?
(2)每台计算机最多需要多长时间可以检测到冲突?
(3)若建立传输速率为 10 Mb/s 的网络,最短帧长为多少?
解:
(1)信号传播延迟 = 总线网长度/信号传播速度:
t = 4000 / ( 2 ∗ 1 0 8 ) = 2 ∗ 1 0 − 5 s t = 4000/(2*10^8)=2*10^{-5}s t=4000/(2∗108)=2∗10−5s → R T T = 2 t = 4 ∗ 1 0 − 5 s RTT = 2t = 4*10^{-5}s RTT=2t=4∗10−5s
(2)检测冲突最长时间是一端发送数据到达另一端时另一端刚发出:
t m a x = 2 t = 4 ∗ 1 0 − 5 s t_{max}=2t=4*10^{-5}s tmax=2t=4∗10−5s
(3)最短帧长 = 双倍传播时延(检测冲突最长时间) * 传输速率:
x m i n = t m a x ∗ v = 4 ∗ 1 0 − 5 ∗ 1 0 7 = 400 b i t = 80 B x_{min}=t_{max}*v=4*10^{-5}*10^7=400bit=80B xmin=tmax∗v=4∗10−5∗107=400bit=80B -
一个速度为 2 Gbps、跨距为 2 km 的 CSMA/CD 网络,假设不使用中继器,传播速率为 5 km/μs,请问该网络的最小帧长是多少?
解:
① 计算 t = 2 / 5 = 0.4 μ s = 4 ∗ 1 0 − 5 s t = 2/5=0.4μs=4*10^{-5}s t=2/5=0.4μs=4∗10−5s
② 最小帧长 x m i n = 2 t ∗ v = 2 ∗ 2 ∗ 1 0 9 ∗ 4 ∗ 1 0 − 5 = 1600 b i t = 200 B x_{min}=2t*v=2*2*10^9*4*10^{-5}=1600bit=200B xmin=2t∗v=2∗2∗109∗4∗10−5=1600bit=200B
相关文章:

CSMA/CD协议之计算最短帧长问题
文章目录 前言CSMA/CD协议计算最短帧长 前言 本篇博客主要论述了如何计算 CSMA/CD 协议下的网络帧长问题,从概念入手,结合例题进行详细的分析。 CSMA/CD协议 概念: ① 载波监听多点接入/碰撞检测 ② 半双工通信 ③ 先听后发、边听边发、冲…...

第三章:什么是分库分表
文章目录 背景什么是分库分表为什么要分库分表性能可用性什么时候考虑分库分表什么时候分库什么时候分表背景 一个系统当伴随着用户量的激增,业务数据的不断增加,数据库表中的数据越来越多,如果再去对我们数据库中的表进行curd操作的时候,就会造成一些性能上的瓶颈问题! …...
)
SpringMVC第六阶段:数据在域中的保存(02)
数据在域中的保存(02) 1、Map或Model或ModelMap形式保存数据在request域中 在四个域中,我们使用最频繁的域就是request对象。往request域对象中,保存数据,还在以下的几种形式。 我们可以在Controller的方法中&#x…...
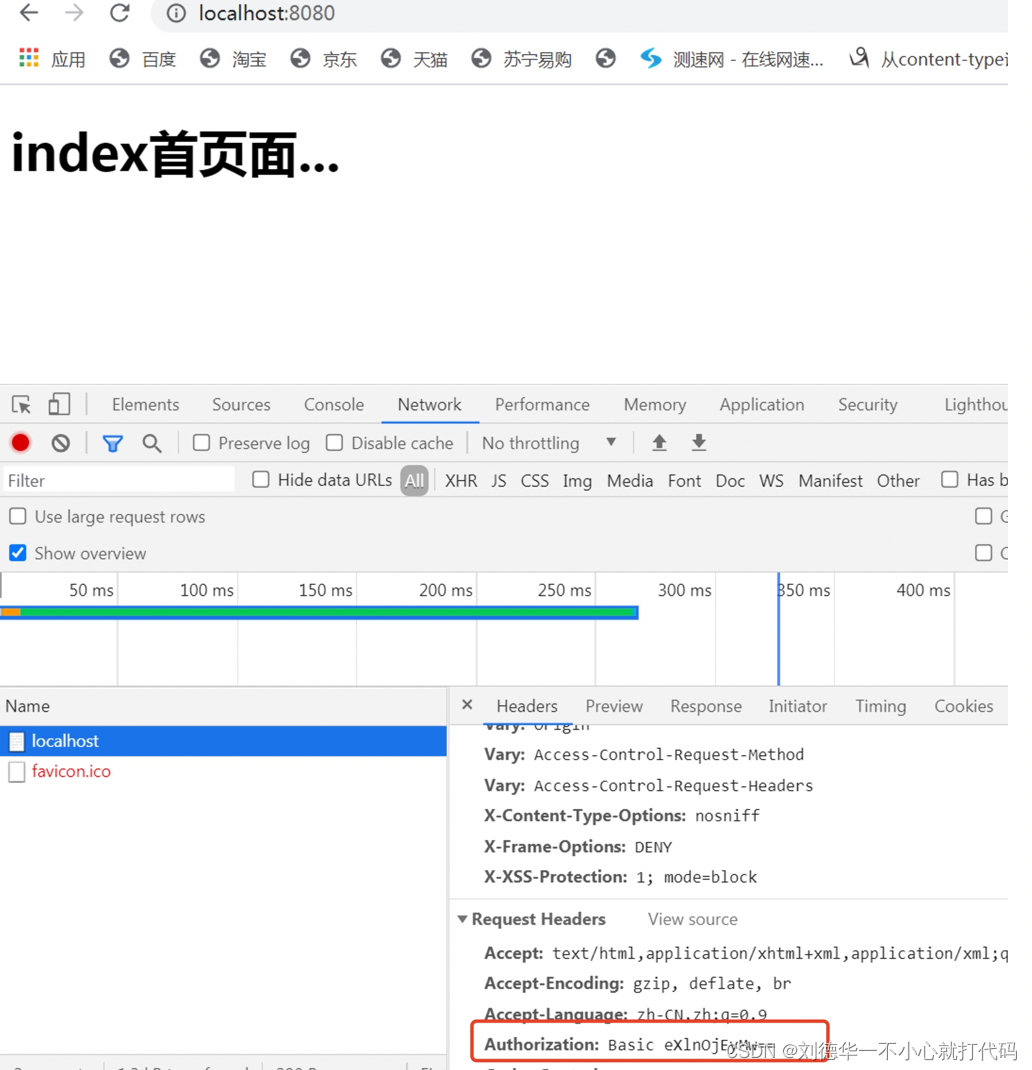
Springboot +spring security,认证方式---HTTP基本认证的实现
一.简介 这篇文章来学习下security的认证方式其中的HTTP基本认证。 二.Spring Security的认证方式 2.1什么是认证 认证: 就是用来判断系统中是否存在某用户,并判断该用户的身份是否合法的过程,解决的其实是用户登录的问题。认证的存在,是…...
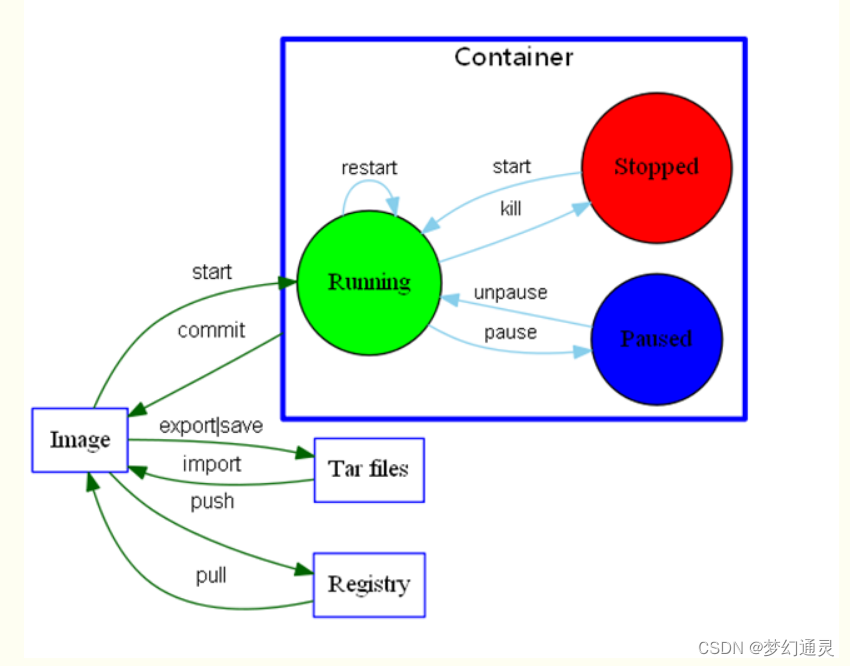
2023年系统分析师案例及论文(回忆版)
2023年5月27日,全国计算机等级上半年考试如期举行 北京市软件分析师考试地点在北京市对外贸易学校,早上外面下起雨,正如考前紧张的心情。 看考场分布图,44个考场,推测有44*301320名考生,本人所在的考场&am…...

数据结构与算法面试题
(1) 红黑树的了解(平衡树,二叉搜索树),使用 场景 把数据结构上几种树集中的讨论一下: 1.AVLtree 定义:最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一…...
C Primer Plus第十章编程练习答案
学完C语言之后,我就去阅读《C Primer Plus》这本经典的C语言书籍,对每一章的编程练习题都做了相关的解答,仅仅代表着我个人的解答思路,如有错误,请各位大佬帮忙点出! 1.修改程序清单10.7的rain.c程序&…...

奇舞周刊第493期:Hook 革命!浅谈 React 新 Hook 的未来与思想
关注前端生态发展,了解行业动向。 下面先一起看下本期周刊 摘要 吧~ 奇舞推荐 ■ ■ ■ Hook 革命!浅谈 React 新 Hook 的未来与思想 作者阳羡曾写文章对 React 新 Hook use 的设计理念和限制进行了深入分析,并提供了一个可能的实现来帮助读者…...
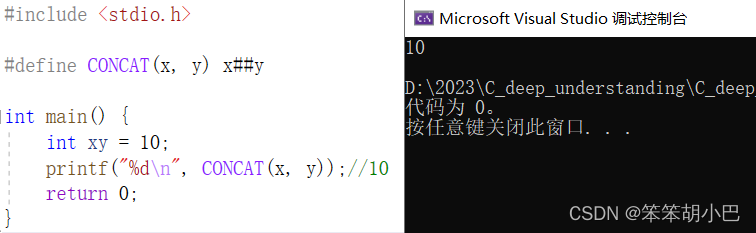
文件包含的本质、预处理符号、# vs ##
何为头文件? 在C语言中,文件包含是一种常见的编程技术,它允许程序员在一个源文件中使用另一个源文件中的函数或变量。 文件包含通常使用#include预处理指令来实现。#include指令告诉预处理器将文件的内容插入到当前文件的指定位置中。 例如&a…...

【JavaSE】Java基础语法(三十九):网络编程入门
文章目录 1. 网络编程概述2. 网络编程三要素3. IP地址4. InetAddress5. 端口和协议 1. 网络编程概述 计算机网络 是指将地理位置不同的具有独立功能的多台计算机及其外部设备,通过通信线路连接起来,在网络 操作系统,网络管理软件及网络通信协…...
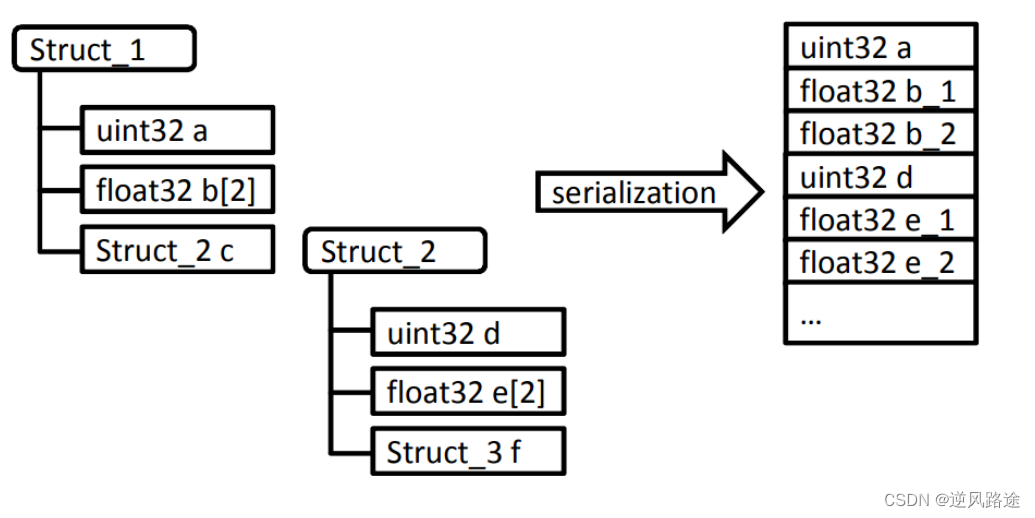
中间件SOME/IP简述
SOME/IP SOME/IP 不是广义上的中间件,严格的来讲它是一种通信协议,但中间件这个概念太模糊了,所以我们也一般称 SOME/IP 为通信中间件。 SOME/IP 全称是 Scalable service-Oriented MiddlewarE over IP。也就是基于 IP 协议的面向服务的可扩…...

[自学记录03|百人计划]移动端GPU的TB(D)R架构基础
一、专有名词解释 1.System on Chip(Soc) Soc是把CPU、GPU、内存、通信基带、GPS模块等等整合在一起的芯片的称呼。常见有A系Soc(苹果),骁龙Soc(高通),麒麟Soc(华为&am…...

详解Java枚举
一、知识点 二、概念 enum 的全称为 enumeration, 是 JDK 1.5 中引入的新特性。 在Java中,被 enum 关键字修饰的类型就是枚举类型。形式如下: enum Color { RED, GREEN, BLUE }如果枚举不添加任何方法,枚举值默认为从0开始的有…...
ES6-ES13学习笔记(4.0)
includes函数 判断字符串是否存在指定字符 <!--* Author: RealRoad1083425287qq.com* Date: 2023-06-01 08:40:33* LastEditors: Mei* LastEditTime: 2023-06-01 08:58:54* FilePath: \vscode\ECMA\05\01.html* Description: * * Copyright (c) 2023 by ${git_name_ema…...

线段树C++详细讲解和个人见解
问题引入 1275. 最大数 给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。 可以对这列数进行两种操作: 添加操作:向序列后添加一个数,序列长度变成 n1;询问操作:询问这个序列中最后 L 个数中…...

构建sysbench的镜像
方式1:先docker run一个镜像,手动安装好commit docker run -it --name mycentos arm64v8/centos:7 /bin/bash docker commit -a "PX Bai" mycentos mycentos1 docker run -it -d --namemycentos1 mycentos1 /bin/bash docker exec -it mycent…...
1201 - 1208 题)
leetcode解题思路分析(一百四十)1201 - 1208 题
丑数3 给你四个整数:n 、a 、b 、c ,请你设计一个算法来找出第 n 个丑数。丑数是可以被 a 或 b 或 c 整除的 正整数 。 容斥原理二分法 class Solution { public:int nthUglyNumber(int n, int a, int b, int c) {long long ab lcm((long long)a, (lo…...
)
FPGA设计的指导性原则 (一)
这一部分主要介绍FPGA/CPLD设计的指导性原则,如FPGA设计的基本原则、基本设 计思想、基本操作技巧、常用模块等。FPGA/CPLD设计的基本原则、思想、技巧和常用模 块是一个非常大的问题,在此不可能面面俱到,只能我们公司项目中常用的一些设计原则与 方法提纲携领地加以介绍,希…...
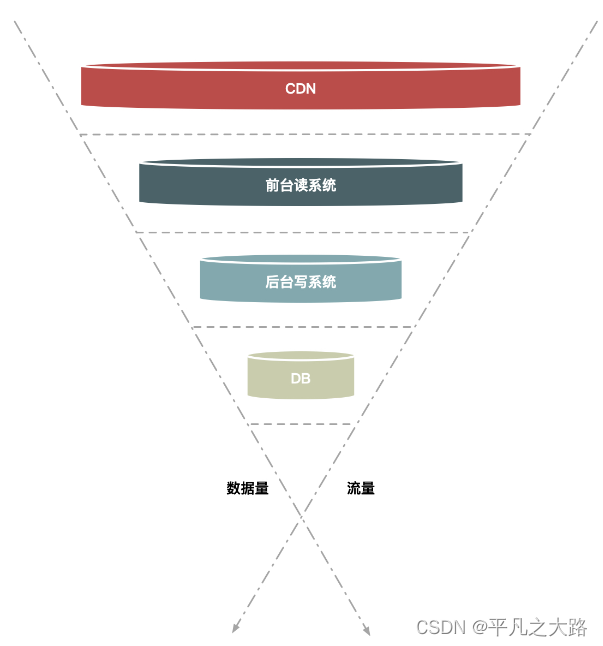
【架构】常见技术点--服务治理
导读:收集常见架构技术点,作为项目经理了解这些知识点以及解决具体场景是很有必要的。技术要服务业务,技术跟业务具体结合才能发挥技术的价值。 目录 1. 微服务 2. 服务发现 3. 流量削峰 4. 版本兼容 5. 过载保护 6. 服务熔断 7. 服务…...
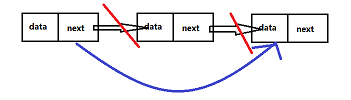
手撕数据结构—单链表
✅作者:简单^不简单 🔥系列专栏:C语言数据结构 💖如果文章有错误,时刻欢迎大家的指正。当然觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝 💬格言:希望我…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
