线段树C++详细讲解和个人见解
问题引入
1275. 最大数
给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。
可以对这列数进行两种操作:
- 添加操作:向序列后添加一个数,序列长度变成 n+1;
- 询问操作:询问这个序列中最后 L 个数中最大的数是多少。
程序运行的最开始,整数序列为空。
一共要对整数序列进行 m 次操作。
写一个程序,读入操作的序列,并输出询问操作的答案。
输入格式
第一行有两个正整数 m,p,意义如题目描述;
接下来 m 行,每一行表示一个操作。
如果该行的内容是 Q L,则表示这个操作是询问序列中最后 L 个数的最大数是多少;
如果是 A t,则表示向序列后面加一个数,加入的数是 (t+a) mod p。其中,t 是输入的参数,a 是在这个添加操作之前最后一个询问操作的答案(如果之前没有询问操作,则 a=0)。
第一个操作一定是添加操作。对于询问操作,L>0�>0 且不超过当前序列的长度。
输出格式
对于每一个询问操作,输出一行。该行只有一个数,即序列中最后 L� 个数的最大数。
数据范围
1≤m≤2×105,
1≤p≤2×109,
0≤t<p
输入样例:
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99
输出样例:
97
97
97
60
60
97
样例解释
最后的序列是 97,14,60,96。
这种题大家一看就知道打暴力,但是一看数据范围就知道只能得部分分。
纯暴力代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int m, p;
int main() {int cnt = 0;cin >> m >> p;int f = 0;for(int i = 1; i <= m; i++) {char k;cin >> k;if(k == 'Q') {int l;cin >> l;int maxn = -1;for(int j = cnt; j >= cnt - l + 1; j--) {maxn = max(a[j], maxn);}cout << maxn << endl;f = maxn;}else {int l;cin >> l;int kk = (l + f) % p;a[++cnt] = kk;}}//for(int i = 1; i <= cnt; i++) cout << a[i] << " ";
}我们之前学过的前缀和算法可以解决区间求和的问题,并且时间复杂度是O(1),但如果涉及到修改操作,前缀和数组都需要重新计算,时间复杂度也是O(n).
那么有没有什么东西能兼顾两者呢?这就是我们要学习的线段树!把修改和查询的时间复杂度都降到O(logn)!!!
算法思想
先来看一下线段树是什么东西!!!
有以下数组(为方便计算,数组下标从1开始)

我们把它转换成线段树,是长这样的:

(1)叶子结点(绿色)存的都是原数组元素的值
(2)每个父结点(sum)是它的两个子节点的值的和
(3)每个父结点记录它表示区间的范围,如上图的“4-5”表示4到5的区间
下面我们看看线段树是如何实现查询和修改操作(和懒标记)的,顺便看看他是如何降低了时间复杂度的。
查询操作
例如我们需要查询2-5区间的和

使用递归的思想:
2~5的和
=2~3的和+4~5的和
=3+0+4~5的和
=3+0+7
=10
总之,就是把查询的区间细化成几个区间的和,在把细化的区间和算出来就行了。
修改操作
例如,我们要把结点6的值由8->7,线段树需要沿着黄色部分一个一个改,直到根结点:

不管是修改操作还是查询操作,时间复杂度都是O(logn),可见线段树的厉害!!!
下一步我们来看如何实现线段树!
算法实现
首先我们需要将原始数组建立成一棵线段树,然后在树的基础上支持区间查询,区间和单点修改的操作。
建树
观察上图,我们发现线段树是一棵近似就是完全二叉树,利用完全二叉树的性质,我们就可以直接用一个数组来存它。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4;
struct node {int l, r, sum;
};
node tree[N * 4 + 10];
int a[N + 10];
void build(int x, int l, int r) {tree[x] = {l, r};//也可以写成tree[x].l = l, tree[x].r = r;//初始化每个节点的左右边界printf("%d:%d %d\n", x, l, r);if(l == r) {tree[x].sum = a[l];//只有叶子节点是真正赋值的,其他节点都要进行pushup操作return;}int mid = l + r >> 1;//递归左右儿子节点build(x << 1, l, mid);build(x << 1 | 1, mid + 1, r);//递归完成后,进行pushup操作tree[x].sum = tree[x * 2].sum + tree[x * 2 + 1].sum;
}
int main() {int n;cin >> n;for(int i = 1; i <= n; i++) {cin >> a[i];}printf("运行结果如下:\n");build(1, 1, n);for(int i = 1; i <= n; i++) {if(n * 2 <= pow(2, i) - 1) {n = i;break;}}for(int i = 1; i <= pow(2, n) - 1; i++) {printf("tree[%d].sum = %d\n", i, tree[i].sum);}printf("在完全二叉树中,0表示这个空间没有数,但是占空间\n");
}运行效果如下:

区间查询
区间查询就是把查询的区间细化成几个区间的和,在把细化的区间和算出来就行了(当然不仅仅局限与求和,求最大值等等也可以实现,改个符号就行了)。
这里以求和为例。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4;
struct node {int l, r, sum;
};
node tree[N * 4 + 10];
int a[N + 10];
void build(int x, int l, int r) {tree[x] = {l, r};//也可以写成tree[x].l = l, tree[x].r = r;//初始化每个节点的左右边界//printf("%d:%d %d\n", x, l, r);if(l == r) {tree[x].sum = a[l];//只有叶子节点是真正赋值的,其他节点都要进行pushup操作return;}int mid = l + r >> 1;//递归左右儿子节点build(x << 1, l, mid);build(x << 1 | 1, mid + 1, r);//递归完成后,进行pushup操作tree[x].sum = tree[x * 2].sum + tree[x * 2 + 1].sum;
}
int query(int x, int l, int r) {//区间查询if(tree[x].l >= l && tree[x].r <= r) return tree[x].sum;//如果该节点的区间被要查找的区间包括了,那么就不用继续找了,直接返回改节点的值就行了int mid = (tree[x].l + tree[x].r) / 2;int sum = 0;if(l <= mid) sum += query(x * 2, l, r);//如果当前节点在要查找区间左边界的右面,那么递归查找左子树if(r > mid) sum += query(x * 2 + 1, l, r);//如果当前节点在要查找区间右边界的左面,那么递归查找右子树return sum;//由此得出了该区间的值,返回即可
}
int main() {int n, m;cin >> n >> m;//n为有n数,m为有m次询问。for(int i = 1; i <= n; i++) {cin >> a[i];}build(1, 1, n);for(int i = 1; i <= m; i++) {int l, r;cin >> l >> r;printf("%d~%d的和为:%lld\n", l, r, query(1, l, r));} return 0;
}运行效果如下:

单点修改
单点修改就是先递归找到要修改的数,然后从这个数一直修改,修改到根节点的过程。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4;
struct node {int l, r, sum;
};
node tree[N * 4 + 10];
int a[N + 10];
void build(int x, int l, int r) {tree[x] = {l, r};//也可以写成tree[x].l = l, tree[x].r = r;//初始化每个节点的左右边界//printf("%d:%d %d\n", x, l, r);if(l == r) {tree[x].sum = a[l];//只有叶子节点是真正赋值的,其他节点都要进行pushup操作return;}int mid = l + r >> 1;//递归左右儿子节点build(x << 1, l, mid);build(x << 1 | 1, mid + 1, r);//递归完成后,进行pushup操作tree[x].sum = tree[x * 2].sum + tree[x * 2 + 1].sum;
}
int query(int x, int l, int r) {//区间查询if(tree[x].l >= l && tree[x].r <= r) return tree[x].sum;//如果该节点的区间被要查找的区间包括了,那么就不用继续找了,直接返回改节点的值就行了int mid = (tree[x].l + tree[x].r) / 2;int sum = 0;if(l <= mid) sum += query(x * 2, l, r);//如果当前节点在要查找区间左边界的右面,那么递归查找左子树if(r > mid) sum += query(x * 2 + 1, l, r);//如果当前节点在要查找区间右边界的左面,那么递归查找右子树return sum;//由此得出了该区间的值,返回即可
}
void change(int now, int x, int k){//单点修改if(tree[now].l == tree[now].r) tree[now].sum = k;//如果找到该节点,修改它else {//printf("%d:%d %d\n", now, x, k);int mid = (tree[now].l + tree[now].r) / 2;//等价于<<1,但是加不加没有区别if(x <= mid) change(now * 2, x, k);else change(now * 2 + 1, x, k);tree[now].sum = tree[now * 2].sum + tree[now * 2 + 1].sum;//pushup操作}
}
int main() {int n, m;cin >> n >> m;//n为有n数,m为有m次询问。for(int i = 1; i <= n; i++) {cin >> a[i];}build(1, 1, n);printf("原来的数组:");cout << "\n";//cout << tree[1].sum << endl;for(int i = 1; i <= 16; i++) printf("tree[%d].sum = %d\n", i, tree[i].sum);change(1, 1, 9);printf("现在的数组:");//cout << tree[1].sum << endl;for(int i = 1; i <= 16; i++) printf("tree[%d].sum = %d\n", i, tree[i].sum);return 0;
}运行效果如下:

还有懒标记没写,改日更新,敬请期待!!!
相关文章:

线段树C++详细讲解和个人见解
问题引入 1275. 最大数 给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。 可以对这列数进行两种操作: 添加操作:向序列后添加一个数,序列长度变成 n1;询问操作:询问这个序列中最后 L 个数中…...

构建sysbench的镜像
方式1:先docker run一个镜像,手动安装好commit docker run -it --name mycentos arm64v8/centos:7 /bin/bash docker commit -a "PX Bai" mycentos mycentos1 docker run -it -d --namemycentos1 mycentos1 /bin/bash docker exec -it mycent…...
1201 - 1208 题)
leetcode解题思路分析(一百四十)1201 - 1208 题
丑数3 给你四个整数:n 、a 、b 、c ,请你设计一个算法来找出第 n 个丑数。丑数是可以被 a 或 b 或 c 整除的 正整数 。 容斥原理二分法 class Solution { public:int nthUglyNumber(int n, int a, int b, int c) {long long ab lcm((long long)a, (lo…...
)
FPGA设计的指导性原则 (一)
这一部分主要介绍FPGA/CPLD设计的指导性原则,如FPGA设计的基本原则、基本设 计思想、基本操作技巧、常用模块等。FPGA/CPLD设计的基本原则、思想、技巧和常用模 块是一个非常大的问题,在此不可能面面俱到,只能我们公司项目中常用的一些设计原则与 方法提纲携领地加以介绍,希…...
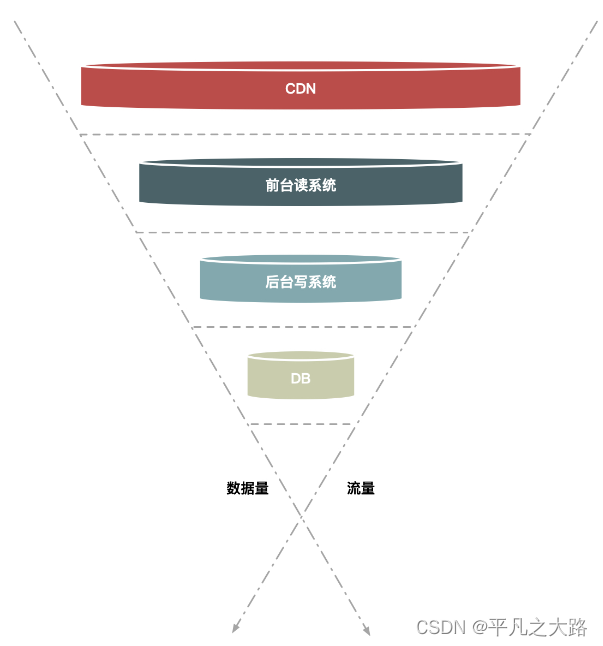
【架构】常见技术点--服务治理
导读:收集常见架构技术点,作为项目经理了解这些知识点以及解决具体场景是很有必要的。技术要服务业务,技术跟业务具体结合才能发挥技术的价值。 目录 1. 微服务 2. 服务发现 3. 流量削峰 4. 版本兼容 5. 过载保护 6. 服务熔断 7. 服务…...
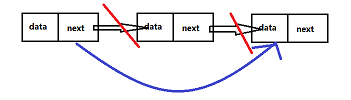
手撕数据结构—单链表
✅作者:简单^不简单 🔥系列专栏:C语言数据结构 💖如果文章有错误,时刻欢迎大家的指正。当然觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝 💬格言:希望我…...

Benewake(北醒) 快速实现 TF02-i-RS485 与电脑通信操作说明
目录 一、前言二、工具准备1. USB-RS485 转接器2. TF02-i-RS4853. 兆信直流电源4.连接线、绝缘胶带、螺丝刀5. PC:Windows 系统6. 串口助手软件 三、连接方式1. USB-RS485 转接板接口说明2. TF02-i-RS485 引脚定义3. 连接图 四、TF02-i-RS485 与电脑通信操作说明1. …...
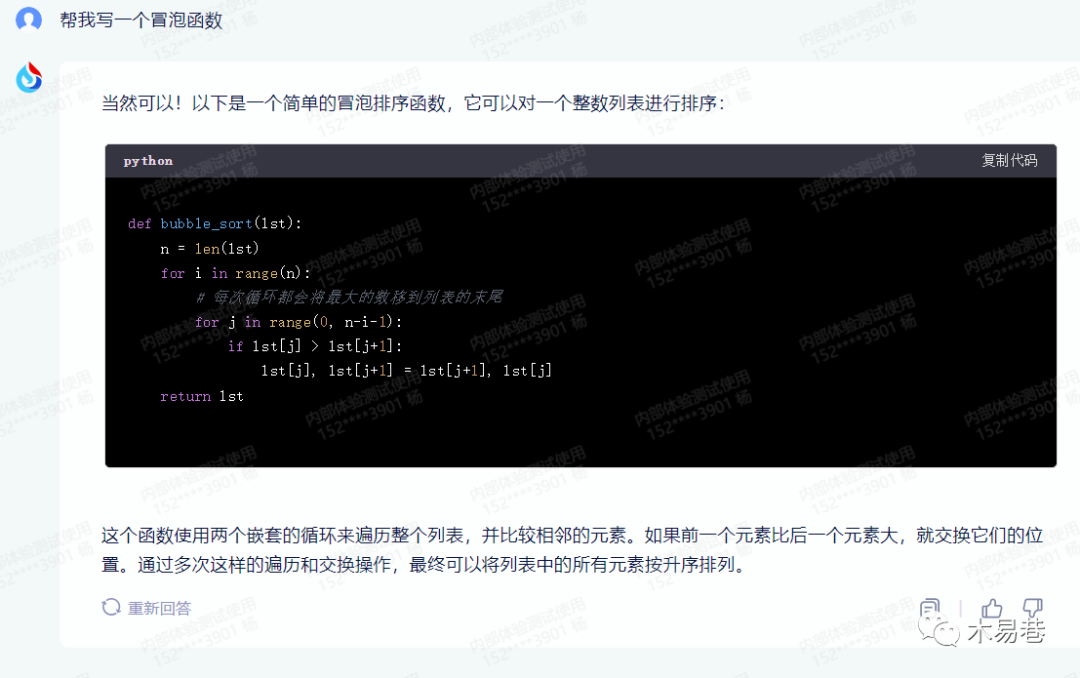
【分享】科大讯飞星火认知大模型(初体验)
前言: 哈喽,大家好,我是木易巷~ 随着人工智能技术的迅猛发展,自然语言处理(NLP)成为了热门话题。在众多NLP模型中,科大讯飞星火认知大模型成为了一个备受瞩目的新秀,今天我们来了解…...

logstash 采集应用日志切割问题
1.logstash [oswatch@rce1 conf]$ cat test.conf input { file { path=>["/tmp/test/test.log*"] } } output { stdout { codec=>rubydebug{} } } 2.python脚本: [oswatch@rce1 conf]$ cat t1.py #!/usr/bin/python # -*- coding: UTF-…...
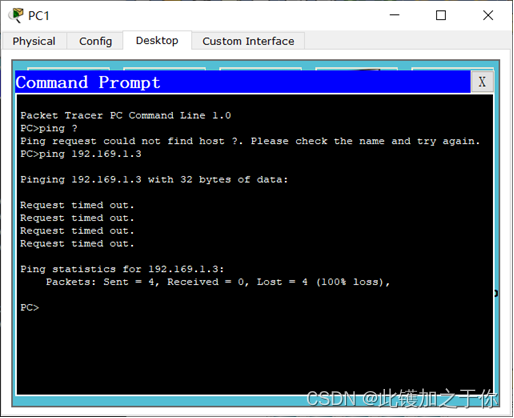
计算机网络实验:认识Packet Tracer软件
目录 前言实验目的实验内容及要求相关知识点实验指导实验过程总结 前言 计算机网络是当今信息技术的重要组成部分,它涉及到多种硬件和软件的协同工作,以实现数据的传输和交换。为了更好地理解和掌握计算机网络的基本原理和技术,我们需要进行…...

【MySQL新手到通关】第六章 时间日期函数
文章目录 1.获取日期时间函数1.1 获取当前日期时间1.2 获取当前日期1.3 获取当前时间 2.日期格式化★★★2.1 日期转指定格式字符串2.2 字符串转日期 3.日期间隔3.1 增加日期间隔 ★★★3.2 减去一个时间间隔★★★3.3 日期相差天数(天)3.4 相差时间&…...

深蓝学院C++基础笔记 第 1 章 C++初探
第 1 章 C初探 1.从Hello World 谈起 Hello World: #include <iostream> int mian() { std::cout << "Hello World!" << std::endl; }函数: 一段能被反复调用的代码,可以接收输入,进行处理并(或)产生输出-返回…...

【配电网重构】基于混合整数二阶锥配电网重构研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Kubernetes mysql 实战以及外部存储处理 [一]
在 Kubernetes 中部署 MySQL 数据库需要考虑以下几个方面: 部署方式:可以选择使用 StatefulSet 或者 Deployment 进行部署,如果需要有状态的服务,使用 StatefulSet 更加合适。存储:MySQL 需要一个持久化存储来保存数据。可以使用 Kubernetes 提供的 PersistentVolumeClaim…...
使用【Python+Appium】实现自动化测试
一、环境准备 1.脚本语言:Python3.x IDE:安装Pycharm 2.安装Java JDK 、Android SDK 3.adb环境,path添加E:\Software\Android_SDK\platform-tools 4.安装Appium for windows,官网地址 Redirecting 点击下载按钮会到GitHub的…...
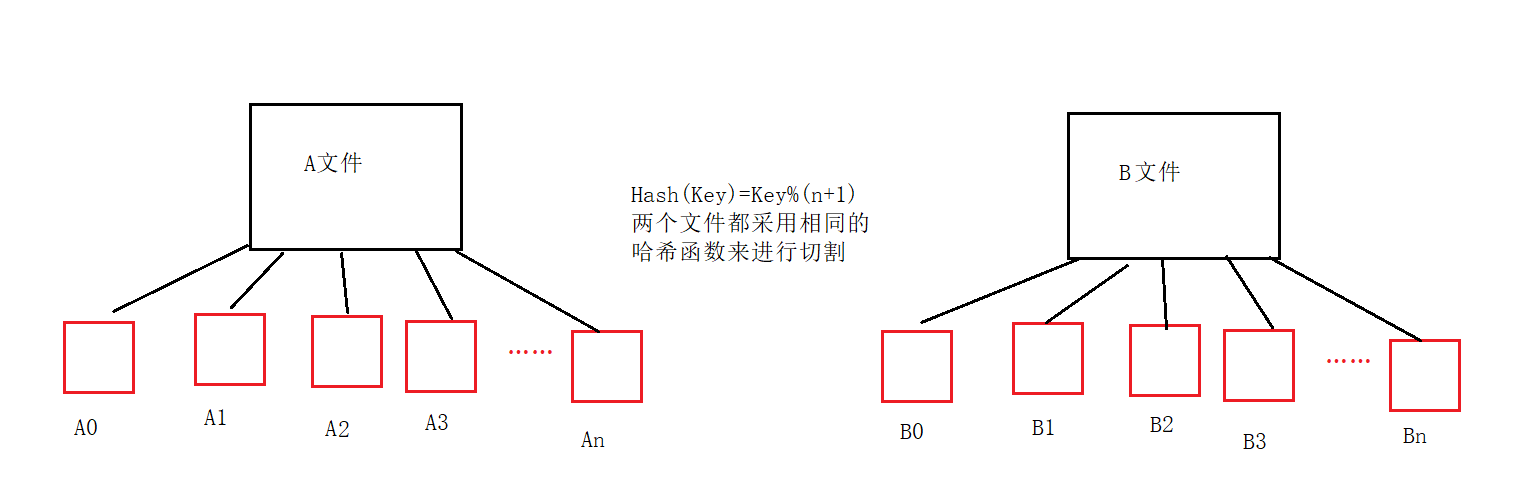
位图和布隆过滤器
位图和布隆过滤器 位图的概念位图的简单模拟实现位图set位图reset位图test 位图总的代码和实现位图的应用布隆过滤器布隆过滤器的简单实现相关操作讨论布隆过滤器的结构设计布隆过滤器插入布隆过滤器查找 布隆过滤器总代码 布隆过滤器优点和缺陷海量数据面试题哈希切割位图应用…...
Eclipse 教程Ⅳ
Eclipse 工作空间(Workspace) eclipse 工作空间包含以下资源: 项目文件文件夹 项目启动时一般可以设置工作空间,你可以将其设置为默认工作空间,下次启动后无需再配置: 工作空间(Workspace)有明显的层次结构。 项目在最顶级&…...

Webpack搭建本地服务器
1 开启本地服务器 2 HMR热模块替换 3 devServer配置 4 开发和生成环境 需要本地服务的目的就在每次我们保存项目源文件的时候都可以自动打包新的打包文件, 这里主要讲webpack-dev-server: 先安装: npm install webpack-dev-server -D 需要…...
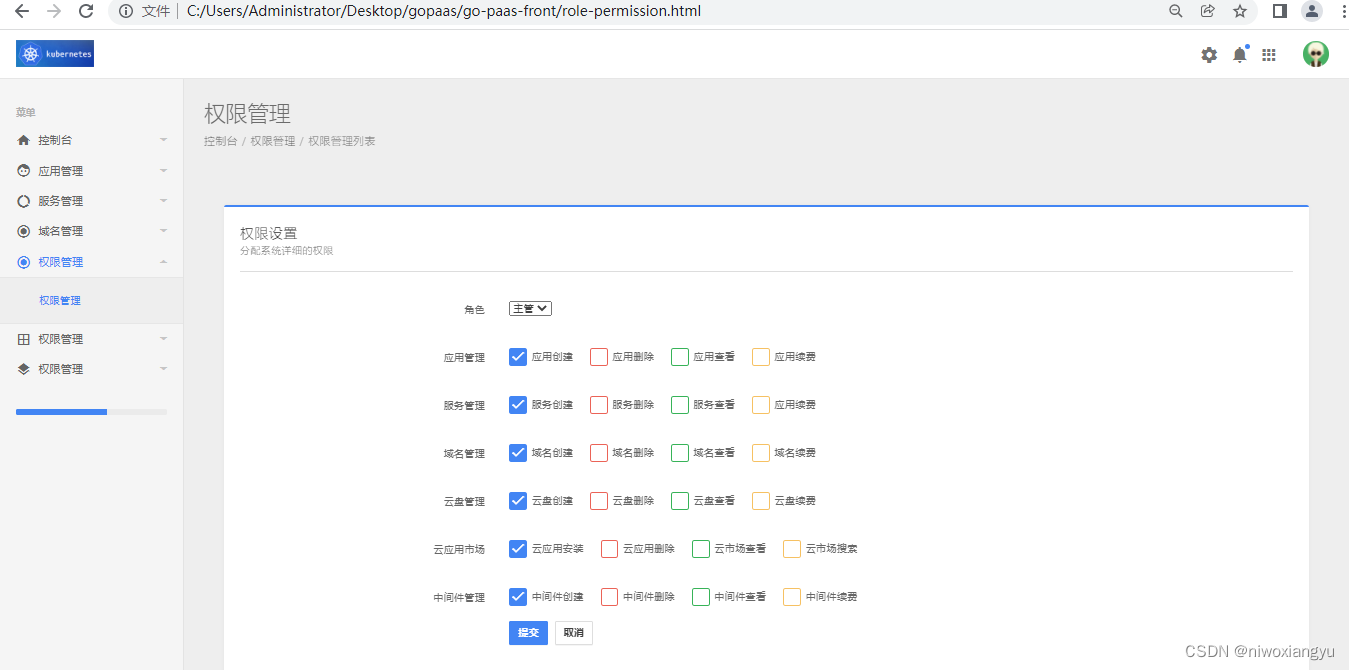
基于Go开发PaaS平台3
Go开发PaaS平台核心功能 代码仓库地址GitHub - yunixiangfeng/gopaas 10-18 中间件前端页面以及核心API开发(中) C:\Users\Administrator\Desktop\gopaas\middlewareapi\handler\middlewareApiHandler.go package handlerimport ("context"…...
虎牙直播在微服务改造的实践总结
博主介绍:✌全网粉丝4W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建与毕业项目实战、定制、远程,博主也曾写过优秀论文,查重率极低,在这方面…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...
