CAP原则
CAP原则又称CAP定理,指的是在一个分布式系统中,存在Consistency(一致性)、Availability(可用性)、Partition tolerance(分区容错性),三者不可同时保证,最多只能保证其中的两者。
一致性(C):在分布式系统中的所有数据备份,在同一时刻都是同样的值(所有的节点无论何时访问都能拿到最新的值)
可用性(A):系统中非故障节点收到的每个请求都必须得到响应(比如我们之前使用的服务降级和熔断,其实就是一种维持可用性的措施,虽然服务返回的是没有什么意义的数据,但是不至于用户的请求会被服务器忽略)
分区容错性(P):一个分布式系统里面,节点之间组成的网络本来应该是连通的,然而可能因为一些故障(比如网络丢包等,这是很难避免的),使得有些节点之间不连通了,整个网络就分成了几块区域,数据就散布在了这些不连通的区域中(这样就可能出现某些被分区节点存放的数据访问失败,我们需要来容忍这些不可靠的情况)
总的来说,数据存放的节点数越多,分区容忍性就越高,但是要复制更新的次数就越多,一致性就越难保证。同时为了保证一致性,更新所有节点数据所需要的时间就越长,那么可用性就会降低。
所以说,只能存在以下三种方案:
AC 可用性+一致性
要同时保证可用性和一致性,代表着某个节点数据更新之后,需要立即将结果通知给其他节点,并且要尽可能的快,这样才能及时响应保证可用性,这就对网络的稳定性要求非常高,但是实际情况下,网络很容易出现丢包等情况,并不是一个可靠的传输,如果需要避免这种问题,就只能将节点全部放在一起,但是这显然违背了分布式系统的概念,所以对于我们的分布式系统来说,很难接受。
CP 一致性+分区容错性
为了保证一致性,那么就得将某个节点的最新数据发送给其他节点,并且需要等到所有节点都得到数据才能进行响应,同时有了分区容错性,那么代表我们可以容忍网络的不可靠问题,所以就算网络出现卡顿,那么也必须等待所有节点完成数据同步,才能进行响应,因此就会导致服务在一段时间内完全失效,所以可用性是无法得到保证的。
AP 可用性+分区容错性
既然CP可能会导致一段时间内服务得不到任何响应,那么要保证可用性,就只能放弃节点之间数据的高度统一,也就是说可以在数据不统一的情况下,进行响应,因此就无法保证一致性了。虽然这样会导致拿不到最新的数据,但是只要数据同步操作在后台继续运行,一定能够在某一时刻完成所有节点数据的同步,那么就能实现最终一致性,所以AP实际上是最能接受的一种方案。
比如我们实现的Eureka集群,它使用的就是AP方案,Eureka各个节点都是平等的,少数节点挂掉不会影响正常节点的工作,剩余的节点依然可以提供注册和查询服务。而Eureka客户端在向某个Eureka服务端注册时如果发现连接失败,则会自动切换至其他节点。只要有一台Eureka服务器正常运行,那么就能保证服务可用**(A),只不过查询到的信息可能不是最新的(C)**
相关文章:

CAP原则
CAP原则又称CAP定理,指的是在一个分布式系统中,存在Consistency(一致性)、Availability(可用性)、Partition tolerance(分区容错性),三者不可同时保证,最多只…...

【PowerQuery】M语言的使用产品和使用场景
当然PowerQuery的M语言应用场景不只是引用在PowerBI和Excel中,它具有广泛的应用场景。目前我们可以在以下产品的使用场景中应用到M语言。 Excel PowerQuery应用Excel通过M语言可以实现整体数据的清洗和重构。 PowerBI 的PowerQuery应用 PowerBI也是通过M语言来实现数据…...

【Linux】遇事不决,可先点灯,LED驱动的进化之路---1
【Linux】遇事不决,可先点灯,LED驱动的进化之路---1 前言: 一、最简单的LED驱动程序 1.1 字符设备驱动程序框架 1.2 程序实战 1.2.1 驱动程序(led_drive_simple.c) 1.2.2 应用程序(led_test_simple.c…...
hive任务reduce步骤卡在99%原因及解决
我们在写sql的时候经常发现读取数据不多,但是代码运行时间异常长的情况,这通常是发生了数据倾斜现象。数据倾斜现象本质上是因为数据中的key分布不均匀,大量的数据集中到了一台或者几台机器上计算,这些数据的计算速度远远低于平均…...

C++11 -- lambda表达式
文章目录 lamaba表达式的引入lambda表达式语法lamabda达式各部分说明捕获列表说明 lamaba表达式底层原理探索 lamaba表达式的引入 在C11之前,如果我们想对自定义类型Goods排序,可以根据姓名,价格,学号按照从大到小或者从小到大的方式排序,可是,这样我们要写额外写6个相关的仿函…...
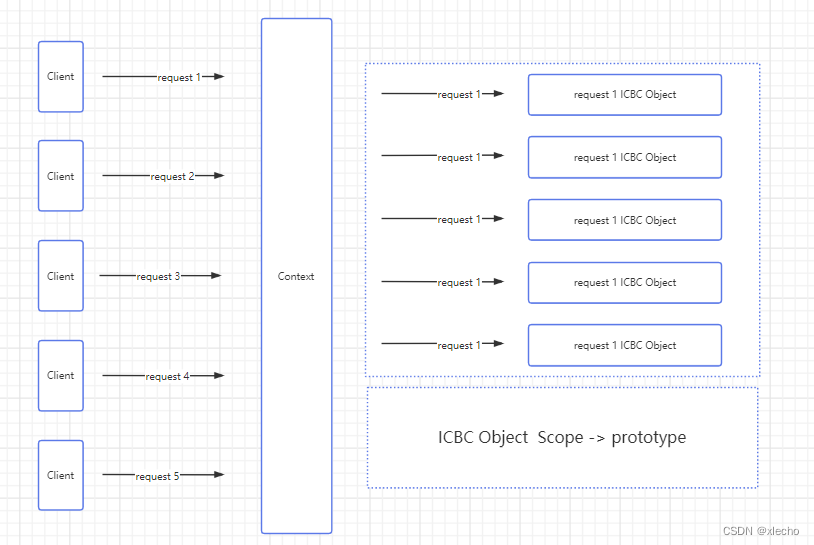
【开源项目】银行查询服务的设计和实现
银行查询服务的设计和实现 项目地址github:https://github.com/xl-echo/bankInquiryService项目地址gitee:https://gitee.com/xl-echo/bank-inquiry-service 银行查询服务的设计初衷是:为提供更加便利的查询服务,我们在分布式系…...

Linux服务器禁止密码登录,设置秘钥登录
生成SSH密钥 (客户机端) 执行ssh-keygen -t rsa命令创建RSA密钥对,执行结果如下(键入3次回车): [rootnode01 .ssh]# ssh-keygen -t rsa Generating public/private rsa key pair. Enter file in which to save the key (/root/.ssh/id_rsa): [回车] En…...

第十八章 开发Productions - ObjectScript Productions - 通过引用或作为输出传递值
文章目录 第十八章 开发Productions - ObjectScript Productions - 通过引用或作为输出传递值典型的回调方法典型的辅助方法 第十八章 开发Productions - ObjectScript Productions - 通过引用或作为输出传递值典型的回调方法典型的辅助方法 第十八章 开发Productions - Object…...

【云原生|Kubernetes】07-Pod健康检查和服务可用性检查
【云原生|Kubernetes】07-Pod健康检查和服务可用性检查 文章目录 【云原生|Kubernetes】07-Pod健康检查和服务可用性检查前言Pod探针Liveness(Pod存活探针)Readiness(Pod服务就绪探针)Startup(启动探针) 定义Liveness存活探针EXec探针HTTP探针TCP探针gRPC探针使用命名端口 定义…...

jeecgboot使用的问题记录
最近使用jeecgboot些项目,总结使用过程中的问题。 form表单 1.下拉框 — 使用字典方式 {label: 工单状态,field: orderStatus,component: JDictSelectTag,componentProps: {dictCode: emergency_order_status,}, } 2.下拉框—使用接口获取数据方式 配置项 { l…...

【C++】数组 - 一维数组,二维数组
文章目录 1. 一维数组1.1 一维数组定义方式1.2 数组名1.3 冒泡排序 2. 二维数组2.1 二维数组定义方式2.2 数组名 所谓数组,就是一个集合,里边存放了相同类型的数据元素。 特点1:数组中的每个数据元素都是相同的数据类型 特点2:数…...

前端:使用rollup的简单记录
目录 rollup安装 简单使用 1、命令行打包 2、配置文件打包 问题 1、报错提示:(node:23744) Warning: To load an ES module, set "type": "module" in the package.json or use the .mjs extension.(Use node --trace-warnings ... to sho…...
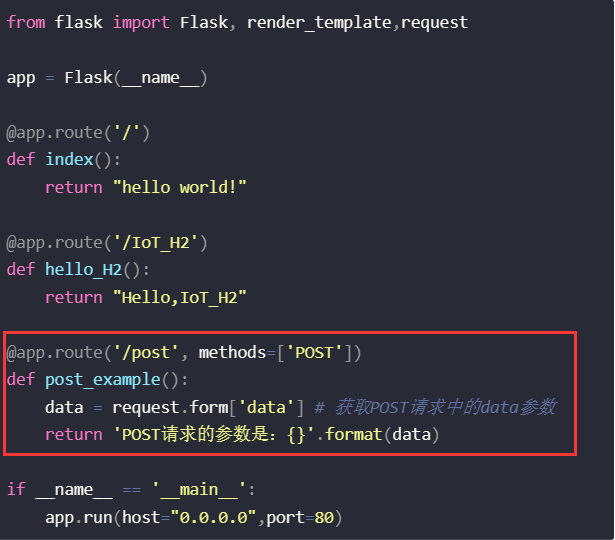
基于flask的web应用开发——接受post请求
目录 0. 前言1. 了解post方法2. 在flask中实现3. 具体讲解 0. 前言 操作系统:Windows10 家庭版 开发环境:Pycahrm Comunity 2022.3 Python解释器版本:Python3.8 第三方库:flask 1. 了解post方法 POST是HTTP协议定义的一种请…...
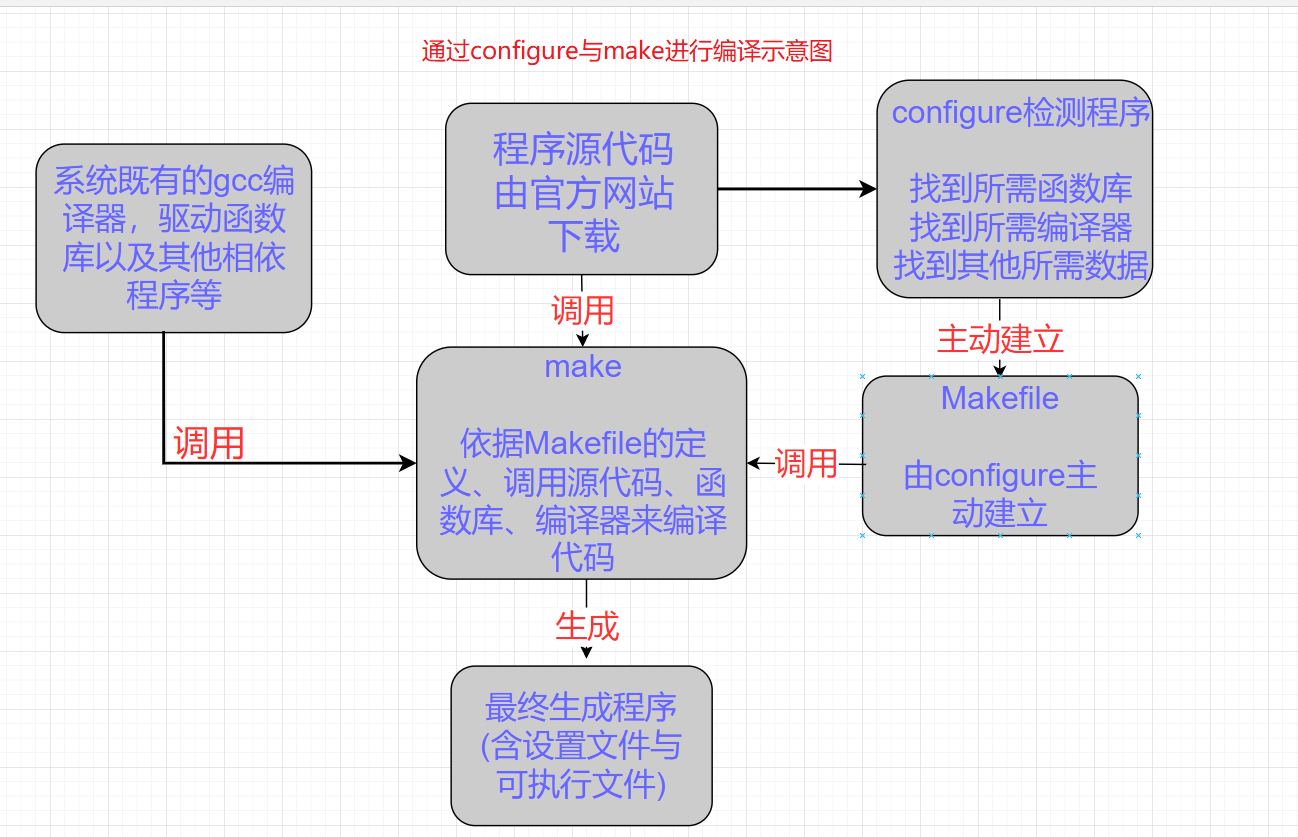
Linux源码包的安装与升级
文章目录 Linux源码包的安装与升级什么是源代码、编译器与可执行文件什么是函数库什么是make与configure什么是Tarball的软件如何安装与升级软件 Linux源码包的安装与升级 如果你想在自己的Linux服务器上运行网站,就需要安装一个Web服务器软件,否则无法…...
电子合同签署协议开源版系统开发
电子合同签署协议开源版系统开发 H5TP6mysqlphp 源码开源不加密 以下是电子合同系统可能包含的功能列表: 用户注册和登录:用户可以注册并登录系统,以便创建、签署和管理合同。合同创建:用户可以创建新合同,包括填写合…...

【每日一题Day221】LC2455可被三整除的偶数的平均值 | 模拟
可被三整除的偶数的平均值【LC2455】 给你一个由正整数组成的整数数组 nums ,返回其中可被 3 整除的所有偶数的平均值。 注意:n 个元素的平均值等于 n 个元素 求和 再除以 n ,结果 向下取整 到最接近的整数。 思路 遍历数组,如果某…...
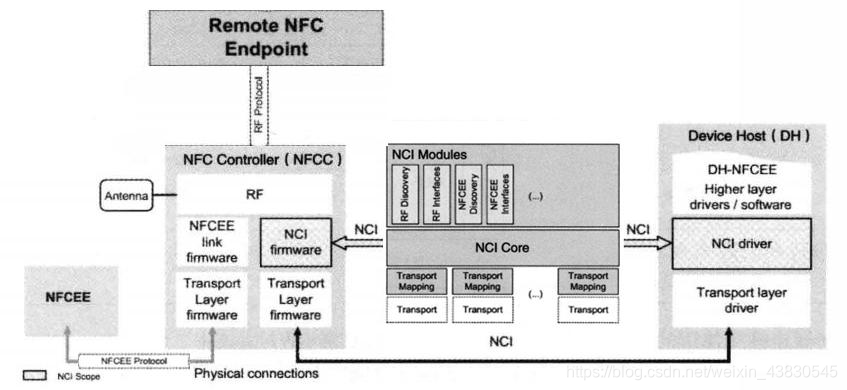
NCI架构-1
1、NFCC和DH通过物理连线相连,物理连线对应为Transport Layer(传输层),支持SPI、I2C、UART、USB等; 2、DH中所有和NFC相关的应用程序都可视为DH-NFCEE(EE:Execution Enviroment),图左的NFCEE模块可运行一些…...

lambda使用场景
字符串转换为数组: [rootmaster pyflink]# cat t300.py f(lambda i: (i, 1)) x11 22 33 print(f(x)) [rootmaster pyflink]# python t300.py (11 22 33, 1) [rootmaster pyflink]# cat t301.py f(lambda i: i[0]) x(aa,11, 22, 33) print(f(x)) [rootmaster pyflink]# pyth…...

Python模拟Postgres数据库连接
psycopg2 psycopg2是一个Python库,用于在Python应用程序中连接和操作PostgreSQL数据库。它是PostgreSQL数据库的官方驱动程序之一,具有广泛的应用和支持。 以下是一些psycopg2的特点和功能: 连接到PostgreSQL数据库:psycopg2提供…...
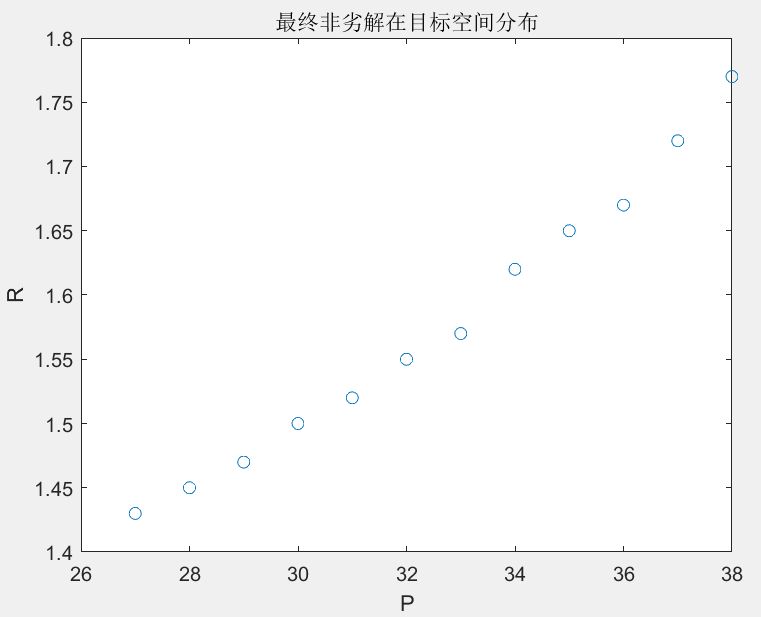
(转载)基于粒子群算法的多目标搜索算法(matlab实现)
1 理论基础 在实际工程优化问题中,多数问题是多目标优化问题。相对于单目标优化问题,多目标优化问题的显著特点是优化各个目标使其同时达到综合的最优值。然而,由于多目标优化问题的各个目标之间往往是相互冲突的,在满足其中一个…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
