(转载)基于粒子群算法的多目标搜索算法(matlab实现)
1 理论基础
2 案例背景
2.1 问题描述

2.2 算法流程
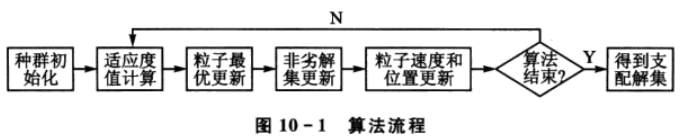
2.3 适应度计算
2.4 筛选非劣解集
2.5 粒子速度和位置更新
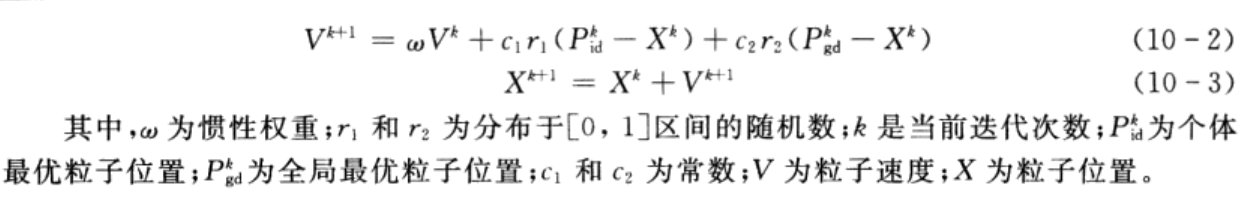
2.6 粒子最优
3 MATLAB程序实现
%% 该函数演示多目标perota优化问题
%清空环境
clc
clearload data%% 初始参数
objnum=size(P,1); %类中物品个数
weight=92; %总重量限制%初始化程序
Dim=5; %粒子维数
xSize=50; %种群个数
MaxIt=200; %迭代次数
c1=0.8; %算法参数
c2=0.8; %算法参数
wmax=1.2; %惯性因子
wmin=0.1; %惯性因子x=unidrnd(4,xSize,Dim); %粒子初始化
v=zeros(xSize,Dim); %速度初始化xbest=x; %个体最佳值
gbest=x(1,:); %粒子群最佳位置% 粒子适应度值
px=zeros(1,xSize); %粒子价值目标
rx=zeros(1,xSize); %粒子体积目标
cx=zeros(1,xSize); %重量约束% 最优值初始化
pxbest=zeros(1,xSize); %粒子最优价值目标
rxbest=zeros(1,xSize); %粒子最优体积目标
cxbest=zeros(1,xSize); %记录重量,以求约束% 上一次的值
pxPrior=zeros(1,xSize);%粒子价值目标
rxPrior=zeros(1,xSize);%粒子体积目标
cxPrior=zeros(1,xSize);%记录重量,以求约束%计算初始目标向量
for i=1:xSizefor j=1:Dim %控制类别px(i) = px(i)+P(x(i,j),j); %粒子价值rx(i) = rx(i)+R(x(i,j),j); %粒子体积cx(i) = cx(i)+C(x(i,j),j); %粒子重量end
end
% 粒子最优位置
pxbest=px;rxbest=rx;cxbest=cx;%% 初始筛选非劣解
flj=[];
fljx=[];
fljNum=0;
%两个实数相等精度
tol=1e-7;
for i=1:xSizeflag=0; %支配标志for j=1:xSize if j~=iif ((px(i)<px(j)) && (rx(i)>rx(j))) ||((abs(px(i)-px(j))<tol)...&& (rx(i)>rx(j)))||((px(i)<px(j)) && (abs(rx(i)-rx(j))<tol)) || (cx(i)>weight) flag=1;break;endendend%判断有无被支配if flag==0fljNum=fljNum+1;% 记录非劣解flj(fljNum,1)=px(i);flj(fljNum,2)=rx(i);flj(fljNum,3)=cx(i);% 非劣解位置fljx(fljNum,:)=x(i,:); end
end%% 循环迭代
for iter=1:MaxIt% 权值更新w=wmax-(wmax-wmin)*iter/MaxIt;%从非劣解中选择粒子作为全局最优解s=size(fljx,1); index=randi(s,1,1); gbest=fljx(index,:);%% 群体更新for i=1:xSize%速度更新v(i,:)=w*v(i,:)+c1*rand(1,1)*(xbest(i,:)-x(i,:))+c2*rand(1,1)*(gbest-x(i,:));%位置更新x(i,:)=x(i,:)+v(i,:);x(i,:) = rem(x(i,:),objnum)/double(objnum);index1=find(x(i,:)<=0);if ~isempty(index1)x(i,index1)=rand(size(index1));endx(i,:)=ceil(4*x(i,:)); end%% 计算个体适应度pxPrior(:)=0;rxPrior(:)=0;cxPrior(:)=0;for i=1:xSizefor j=1:Dim %控制类别pxPrior(i) = pxPrior(i)+P(x(i,j),j); %计算粒子i 价值rxPrior(i) = rxPrior(i)+R(x(i,j),j); %计算粒子i 体积cxPrior(i) = cxPrior(i)+C(x(i,j),j); %计算粒子i 重量endend%% 更新粒子历史最佳for i=1:xSize%现在的支配原有的,替代原有的if ((px(i)<pxPrior(i)) && (rx(i)>rxPrior(i))) ||((abs(px(i)-pxPrior(i))<tol)...&& (rx(i)>rxPrior(i)))||((px(i)<pxPrior(i)) && (abs(rx(i)-rxPrior(i))<tol)) || (cx(i)>weight) xbest(i,:)=x(i,:);%没有记录目标值pxbest(i)=pxPrior(i);rxbest(i)=rxPrior(i);cxbest(i)=cxPrior(i);end%彼此不受支配,随机决定if ~( ((px(i)<pxPrior(i)) && (rx(i)>rxPrior(i))) ||((abs(px(i)-pxPrior(i))<tol)...&& (rx(i)>rxPrior(i)))||((px(i)<pxPrior(i)) && (abs(rx(i)-rxPrior(i))<tol)) || (cx(i)>weight) )...&& ~( ((pxPrior(i)<px(i)) && (rxPrior(i)>rx(i))) ||((abs(pxPrior(i)-px(i))<tol) && (rxPrior(i)>rx(i)))...||((pxPrior(i)<px(i)) && (abs(rxPrior(i)-rx(i))<tol)) || (cxPrior(i)>weight) )if rand(1,1)<0.5xbest(i,:)=x(i,:);pxbest(i)=pxPrior(i);rxbest(i)=rxPrior(i);cxbest(i)=cxPrior(i);endendend%% 更新非劣解集合px=pxPrior;rx=rxPrior;cx=cxPrior;%更新升级非劣解集合s=size(flj,1);%目前非劣解集合中元素个数%先将非劣解集合和xbest合并pppx=zeros(1,s+xSize);rrrx=zeros(1,s+xSize);cccx=zeros(1,s+xSize);pppx(1:xSize)=pxbest;pppx(xSize+1:end)=flj(:,1)';rrrx(1:xSize)=rxbest;rrrx(xSize+1:end)=flj(:,2)';cccx(1:xSize)=cxbest;cccx(xSize+1:end)=flj(:,3)';xxbest=zeros(s+xSize,Dim);xxbest(1:xSize,:)=xbest;xxbest(xSize+1:end,:)=fljx;%筛选非劣解flj=[];fljx=[];k=0;tol=1e-7;for i=1:xSize+sflag=0;%没有被支配%判断该点是否非劣for j=1:xSize+s if j~=iif ((pppx(i)<pppx(j)) && (rrrx(i)>rrrx(j))) ||((abs(pppx(i)-pppx(j))<tol) ...&& (rrrx(i)>rrrx(j)))||((pppx(i)<pppx(j)) && (abs(rrrx(i)-rrrx(j))<tol)) ...|| (cccx(i)>weight) %有一次被支配flag=1;break;endendend%判断有无被支配if flag==0k=k+1;flj(k,1)=pppx(i);flj(k,2)=rrrx(i);flj(k,3)=cccx(i);%记录非劣解fljx(k,:)=xxbest(i,:);%非劣解位置endend%去掉重复粒子repflag=0; %重复标志k=1; %不同非劣解粒子数flj2=[]; %存储不同非劣解fljx2=[]; %存储不同非劣解粒子位置flj2(k,:)=flj(1,:);fljx2(k,:)=fljx(1,:);for j=2:size(flj,1)repflag=0; %重复标志for i=1:size(flj2,1)result=(fljx(j,:)==fljx2(i,:));if length(find(result==1))==Dimrepflag=1;%有重复endend%粒子不同,存储if repflag==0 k=k+1;flj2(k,:)=flj(j,:);fljx2(k,:)=fljx(j,:);endend%非劣解更新flj=flj2;fljx=fljx2;end%绘制非劣解分布
plot(flj(:,1),flj(:,2),'o')
xlabel('P')
ylabel('R')
title('最终非劣解在目标空间分布')
disp('非劣解flj中三列依次为P,R,C')3.1 仿真结果
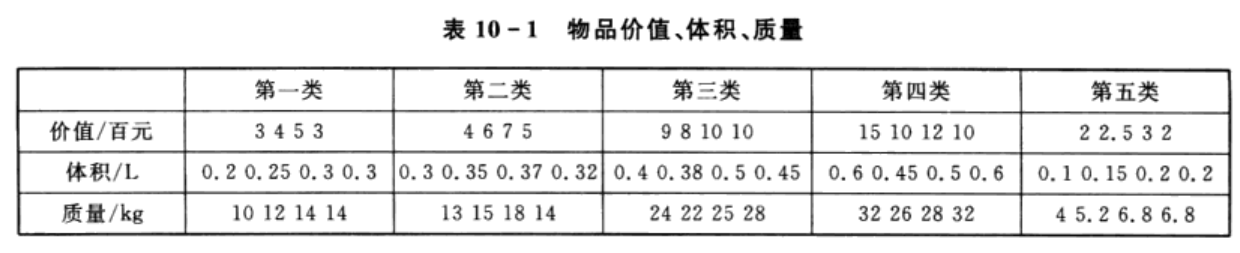
4 延伸阅读
相关文章:

(转载)基于粒子群算法的多目标搜索算法(matlab实现)
1 理论基础 在实际工程优化问题中,多数问题是多目标优化问题。相对于单目标优化问题,多目标优化问题的显著特点是优化各个目标使其同时达到综合的最优值。然而,由于多目标优化问题的各个目标之间往往是相互冲突的,在满足其中一个…...
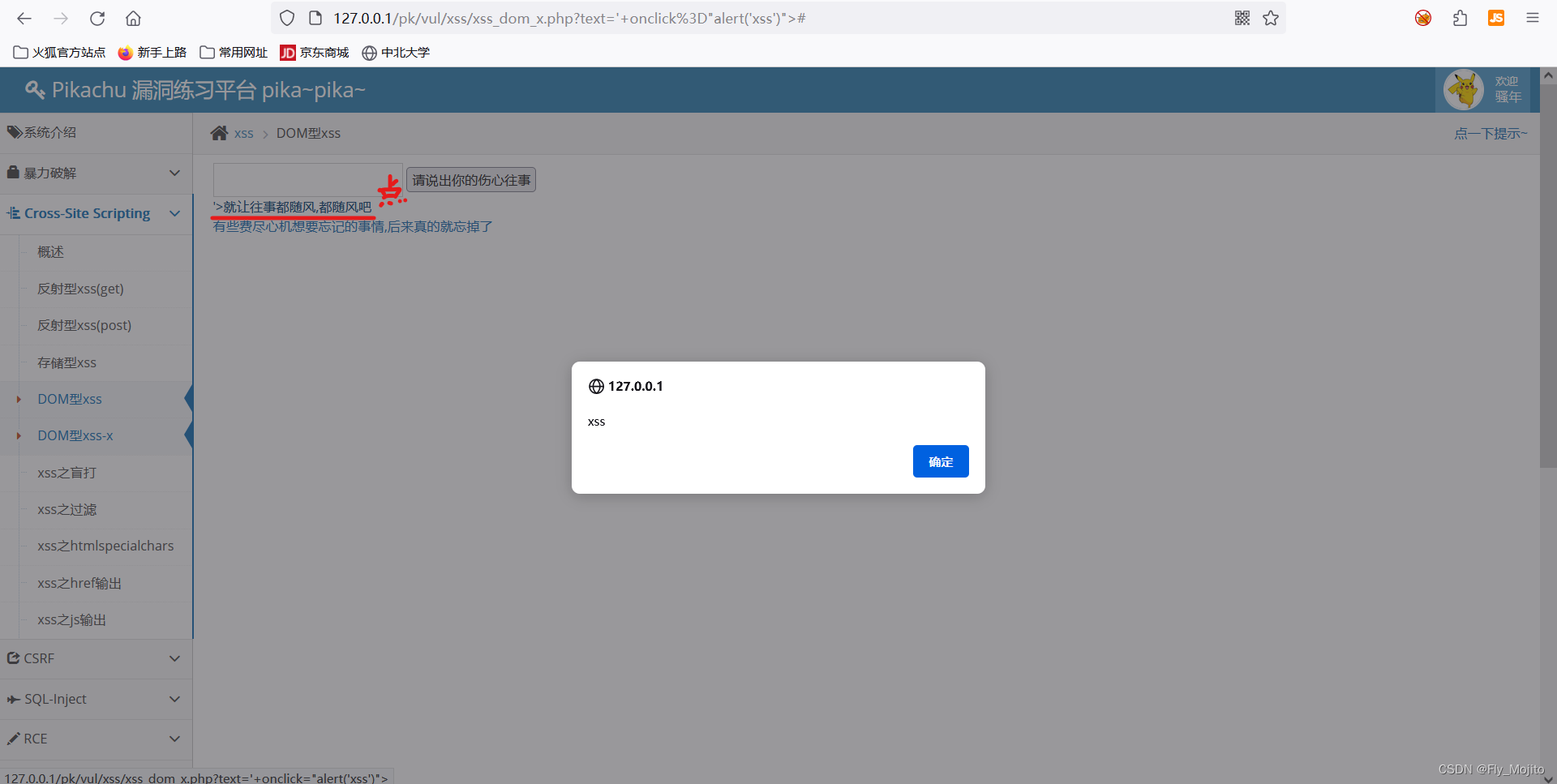
皮卡丘存储型xss、DOM型xss、DOM型xss-x
1.存储型xss 看题目,我们先留言,看它的过滤机制 发现可以永久存储并输出我们的留言 之后插入payload: <script>alert(xss)</script> 成功弹窗! 2.DOM型xss Dom型xss,简单的说,就是向文档对象传入xss参…...
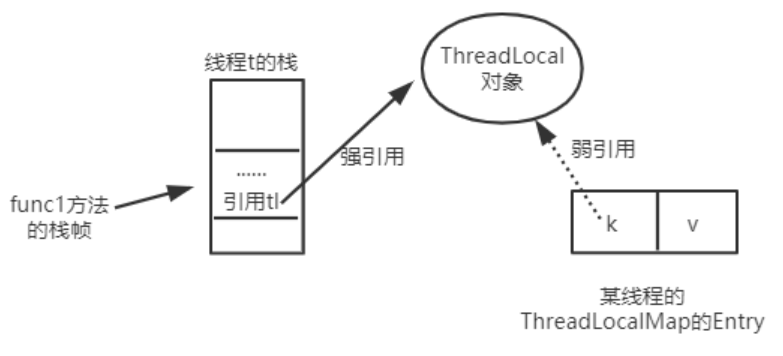
ThreadLocal源码
介绍 ThreadLocal是一个线程的本地变量,也就意味着这个变量是线程独有的,是不能与其他线程共享的。这样就可以避免资源竞争带来的多线程的问题。 但是,这种解决多线程安全问题的方式和加锁方式(synchronized、Lock) 是有本质的区…...
数据操作、查询)
Hive学习---3、DML(Data Manipulation Language)数据操作、查询
1、DML(Data Manipulation Language)数据操作 1.1 Load load语句可将文件导入到Hive表中 1、语法 load data [local] inpath filepath [overwrite] into table tablename [partition(partcol1val1,partcol2val2...)]2、关键字说明 (1&…...

chatgpt赋能python:Python去除重复元素的几种方法
Python去除重复元素的几种方法 在Python编程中,去除列表、集合、字典等数据结构中的重复元素是一个常见的操作。本文将介绍Python中去除重复元素的几种方法,并分析它们的优缺点。 方法一:使用set去重 Set是Python中的一种集合类数据结构&a…...
2年测试我迷茫了,软件测试大佬都会哪些技能?我的测试进阶之路...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 Python自动化测试&…...

21天学会C++:Day7----auto关键字
CSDN的uu们,大家好。这里是C入门的第七讲。 座右铭:前路坎坷,披荆斩棘,扶摇直上。 博客主页: 姬如祎 收录专栏:C专题 目录 1. 知识引入 2. auto的使用 2.1 auto与指针和引用结合起来使用 2.2 在同一…...

Vue3 + ElementPlus实战学习——模拟简单的联系人列表管理后台
文章目录 📋前言🎯demo 介绍🎯功能分析🧩数据的展示与分页功能🧩编辑功能🧩删除功能 🎯部分代码分析🎯完整代码📝最后 📋前言 这篇文章介绍一下基于 Vue3 和…...
【Go语言从入门到实战】并发篇
Go语言从入门到实战 — 并发篇 协程 Thread vs Groutine 相比之下,协程的栈大小就小很多了,创建起来也会更快,也更节省系统资源。 一个 goroutine 的栈,和操作系统线程一样,会保存其活跃或挂起的函数调用的本地变量…...
)
img标签请求 添加自定义header(二)
之前写过一篇关于img添加自定义请求头的处理方式(点击这里),那么本篇我们来看另外几种实现方法。 自定义指令 以Vue为例,我们可以定义一个全局指令,对img标签进行一些处理。 <template><img :src"src…...

Set和weakSet Map和WeakMap
Set和weakSet的用法和区别 1.Set 和weakSet 它是类似于数组,且成员值都是唯一的, 2.Set有 add has delete clear size keys values forEach entries 3.weakSet 有add has delete 4.WeakSet中只能存放对象类型,不能存放基本类型 5.WeakSet它是…...

Qt基础之三十六:异常处理
本文将介绍如何在Qt中使用try...catch和调试dump文件来处理异常。 Qt版本5.12.6 一.使用try...catch 一段简单的捕获异常的代码,新建一个控制台工程,pro文件不用修改 #include <QCoreApplication> #include <QDebug>int main(int argc, char *argv[]) {QCoreA…...

【HMS Core】【ML Kit】活体检测FAQ合集
【问题描述1】 使用示例代码集成活体检测SDK时,报错state code -7001 【解决方案】 使用示例代码前请详细阅读示例工程中的“README”文件。您需要完成以下操作后才可以运行示例代码。 在AppGallery Connect网站下载自己应用的“agconnect-services.json”文件&a…...

ChatGPT:使用OpenAI创建自己的AI网站,使用 flask web框架快速搭建网站主体
使用OpenAI创建自己的AI网站 如果你还是一个OpenAI的小白,有OpenAI的账号,但想调用OpenAI的API搞一些有意思的事,那么这一系列的教程将仔细的为你讲解如何使用OpenAI的API制作属于自己的AI网站。 使用 flask web框架快速搭建网站主体 之前…...
后端(一):Tomcat
我们之前的前端是被我们一笔带过的,那不是我们要讲的重点,而这里的后端则是重点。本章先来认识认识后端的基础。 Tomcat 是什么 我们先来聊聊什么叫做tomcat,我们熟悉的那个是汤姆猫: 这和我们Java世界中的Tomcat 不是同一只猫&…...
)
华为OD机试之最小调整顺序次数、特异性双端队列(Java源码)
最小调整顺序次数、特异性双端队列 题目描述 有一个特异性的双端队列,该队列可以从头部或尾部添加数据,但是只能从头部移出数据。 小A依次执行2n个指令往队列中添加数据和移出数据。其中n个指令是添加数据(可能从头部添加、也可能从尾部添加…...

2023年武汉住建厅七大员怎么报名?报名流程?精准题库一次过??
2023年武汉住建厅七大员怎么报名?报名流程?精准题库一次过?? 2023年武汉住建厅七大员是指施工员、质量员、资料员、材料员、机械员、标准员、劳务员,报的最多的可能就是施工员,质量员和资料员 报名流程: 1…...

Rust每日一练(Leetday0014) 组合总和II、缺失正数、接雨水
目录 40. 组合总和 II Combination Sum II 🌟🌟 41. 缺失的第一个正数 First Missing Positive 🌟🌟🌟 42. 接雨水 Trapping Rain Water 🌟🌟🌟 🌟 每日一练刷题…...
EnjoyVIID部署
1、下载 git clone https://gitee.com/tsingeye/EnjoyVIID.git 2、导入数据库 创建表enjoyviid 导入数据库(修改数据库文件里的编码) EnjoyVIID/sql/tsingeye-viid.sql 3、修改配置 vim EnjoyVIID/tsingeye-admin/src/main/resources/application-dev.yml 修改数据库连接、re…...

用Python解决爱因斯坦的数学问题
1 问题 有一条阶梯,若每步跨2阶,则剩最后一阶,若每步跨3阶,则最后剩2阶,若每步跨5阶,则最后剩4阶,若每步跨6阶,则最后剩5阶,只有每次跨7阶,最后才刚好不剩&am…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
