剑指offer打卡
这里写目录标题
- day1 二叉树和为某一路径
- day2复杂链表的复刻
- day3二叉搜索树与双向链表
- day4数字排列
- day5找出出现次数超过一半的次数
- day6 二进制中1的个数
- day7 二叉树的最近公共祖先
- day8 字符串转换为整数
- day9 构建乘积数组
- day10不用加减乘除的加法
- day11求1+2....+n
- day11 股票的最大价值
- day13扑克牌的顺子
- day14骰子的点数
- day15滑动窗口的最大值
day1 二叉树和为某一路径

思路分析
- 初步想法:这个题就是一个典型的爆搜问题,我们最简单的一个想法就是,搜索所有路径,并求和进行判断,所以我们可以使用dfs模板
- 简化:为了判断是否于tar相等,我们需要每次递归时都传入,sum,tar两个参数,我们可以将加法转化为减法,与0进行比较
- 在这里我们需要使用递归函数,所以采用递归三步法进行分析:定义,终止条件,单层逻辑;
class Solution {static List<List<Integer>> ans;static List<Integer> res=new ArrayList<>();public List<List<Integer>> findPath(TreeNode root, int sum) {ans=new ArrayList<>();dfs(root,sum);return ans;}//1.定义:对路径进行搜索,无返回值public static void dfs(TreeNode root,int sum){//2.递归终止条件,当传入节点为null时,则无需进行下一步递归。if(root==null)return;//如果为null则直接返回//3.单层逻辑res.add(root.val);//3.1将该值加入ressum=sum-root.val;//3.2并用sum减去该值//3.3判断此时的节点是否符合要求//**********重点**********/*为什么在ans.add(new ArrayList<>(res)) 要重新建立一个list?*答:在该题中res为成员变量,所有的方法共享一个,指向同一地址;*如果直接加入,在后续语句中,依旧会修改res,导致其答案不一样**/if(root.left==null && root.right==null && sum==0)ans.add(new ArrayList<>(res));//3.4递归处理左右子树dfs(root.left,sum);dfs(root.right,sum);res.remove(res.size()-1);//恢复现状,如果该条路不同则,退出该值,}day2复杂链表的复刻
思路分析
- 首先我们可以使用hash表存储每个点对应的来next指针 random指针,而后复现
- 在这里我们还有另一种做法:
1. 在每个点对应的后面复制每一个点
2. 遍历链表处理random指针
3. 将这两条互相交叉的链分开(必须将原有链恢复原样,不然会报错)
class Solution {public ListNode copyRandomList(ListNode head) {//1.在原链表的每一个节点后加上节点的复制if(head==null)return null;for(ListNode p = head ; p != null;){ListNode q = new ListNode(p.val);//防止断链ListNode next = p.next;p.next = q;q.next = next;p = next;}//2.将新加入的节点的random指针指向原链表的random指针for(ListNode p = head ; p != null ; p = p.next.next){if(p.random != null){//新节点的random指针指向原节点random指针指向的下一个节点p.next.random = p.random.next;}}//3.将两条链分开ListNode dummy = new ListNode(-1);ListNode cur = dummy;for(ListNode p = head; p != null; p = p.next){cur.next = p.next;cur = cur.next;// 前面破坏了原head链表,恢复链表p.next = p.next.next;
}return dummy.next;}
}
day3二叉搜索树与双向链表

思路分析
- 我们可以知道对于一个二叉搜索树,中序遍历与有序列表的元素顺序相同
- 所以我们在这里使用中序遍历的模板
- 对于中序遍历会先重最左边的节点(4)开始处理
class Solution {//指针:用来记录前一个节点·static TreeNode pre=null;public TreeNode convert(TreeNode root) {if(root==null)return null;dfs(root);while(root.left!=null)root=root.left;return root;}//我们一第一个节点4[6]来讲解这个单层逻辑 //1.函数定义:将二叉搜索树变为有序的双向链表,无返回值public static void dfs(TreeNode root){//2.递归终止条件:若节点为空,则结束if(root==null)return;dfs(root.left);//由于中序遍历,所以root 会依次是 4 6 8 10 .。。。root.left=pre;// null<—4(<-6)[4<—6]if(pre!=null)pre.right=root;//pre为空不执行 [4—>(<——)6]pre=root;//pre=4;[pre=6]dfs(root.right);}}
day4数字排列
思路分析
- 很容易知道这里应该使用回溯算法求解,很经典
class Solution {static List<Integer> path;static boolean[] st;//该数是否被使用static Set<List<Integer>> res;static int n;public List<List<Integer>> permutation(int[] nums) {path=new ArrayList<>();st=new boolean[nums.length];res=new HashSet<>();n=nums.length;dfs(0,nums);List<List<Integer>> ans=new ArrayList<>(res);return ans;}public static void dfs(int u,int[] nums){if(u==n){res.add(new ArrayList<>(path));return;}for(int i=0;i<n;i++){if(!st[i]){path.add(nums[i]);st[i]=true;dfs(u+1,nums);st[i]=false;path.remove(path.size()-1);}}}
}
day5找出出现次数超过一半的次数
class Solution {public int moreThanHalfNum_Solution(int[] nums) {int cnt=1,val=nums[0];for(int i=0;i<nums.length;i++){if(nums[i]==val)cnt++;else cnt--;//如果出现问题则进行重置if(cnt==0){val=nums[i];cnt=1;}}return val;}
}
测试例子解析
- 例1:input([1,2,1,1,3])
i=0:nums[i]=1,val=1,cnt=2
i=1:nums[i]=2,val=1,cnt=1
i=2:nums[i]=1,val=1,cnt=2
i=3:nums[i]=1,val=1,cnt=3
i=4:nums[i]=3,val=1,cnt=2
例2:input([2,0,1,1,3])
i=0:nums[i]=2,val=2,cnt=2
i=1:nums[i]=0,val=2,cnt=1
i=2:nums[i]=1,val=2,cnt=0,重置,val=1,cnt=1
i=3:nums[i]=1,val=1,cnt=2
i=4:nums[i]=3,val=1,cnt=1
day6 二进制中1的个数

基本知识点
- 计算机中数的二进制表示
3:00000011
-3:使用补码进行表示
先计算-3绝对值的二进制 00000011
取反:11111100
加1:11111101(这就是计算级的-3表示)
- 无符号整数:计算机里的数是用二进制表示的,最左边的这一位一般用来表示这个数是正数还是负数,这样的话这个数就是有符号整数。无符号整数包括0和正数。
举例:假设有一个 数据类型有8位组成
无符号整数:8位全部表示数值;范围位[0,2^8-1]
有符号整数:最左边表示符号,后7位表示数值;范围[-111 1111,+111 1111]
- 位运算
un&1:将二进制的个位取出
un>>>1:将个位删掉
思路分析
如果n位正数(0),我们直接挨个将每一位数字取出计算即可
负数:我们可以将负数先转换位无符号整数,在进行与正数相同操作
class Solution {public int NumberOf1(int n) {int res=0;int un=n & 0xffffffff;//将数字转换为无符号整数;0xffffffff表示32个1while(un!=0){res=res+(un&1);un=un>>>1;}return res;}
}
day7 二叉树的最近公共祖先
 这里推荐一个大佬的题解
这里推荐一个大佬的题解
大佬题解(非常详细有用)
思路分析
day8 字符串转换为整数
思路分析
按照以下步骤就可以
- 最前面的空格
- 判断符号
- 数位相乘计算整数
- char 转换位数字 :char-‘0’
class Solution {public int strToInt(String str) {long res=0;char[] ch=str.toCharArray();int k=0;//去除空格while(k<ch.length && ch[k]==' ')k++;int flag=1;if(k<ch.length && ch[k]=='-'){flag=-1;k++;}else if(k<ch.length && ch[k]=='+') k++;// System.out.println(k<ch.length && ch[k]>='0' && ch[k]<='9');while(k<ch.length && ch[k]>='0' && ch[k]<='9'){// System.out.println(ch[k]-'0');res=res*10+(ch[k]-'0');if (res > 1e11) break;k++;}// System.out.println(res);res=(res*flag);if (res > Integer.MAX_VALUE) res = Integer.MAX_VALUE;if (res < Integer.MIN_VALUE) res = Integer.MIN_VALUE;return (int)res;}
}
day9 构建乘积数组
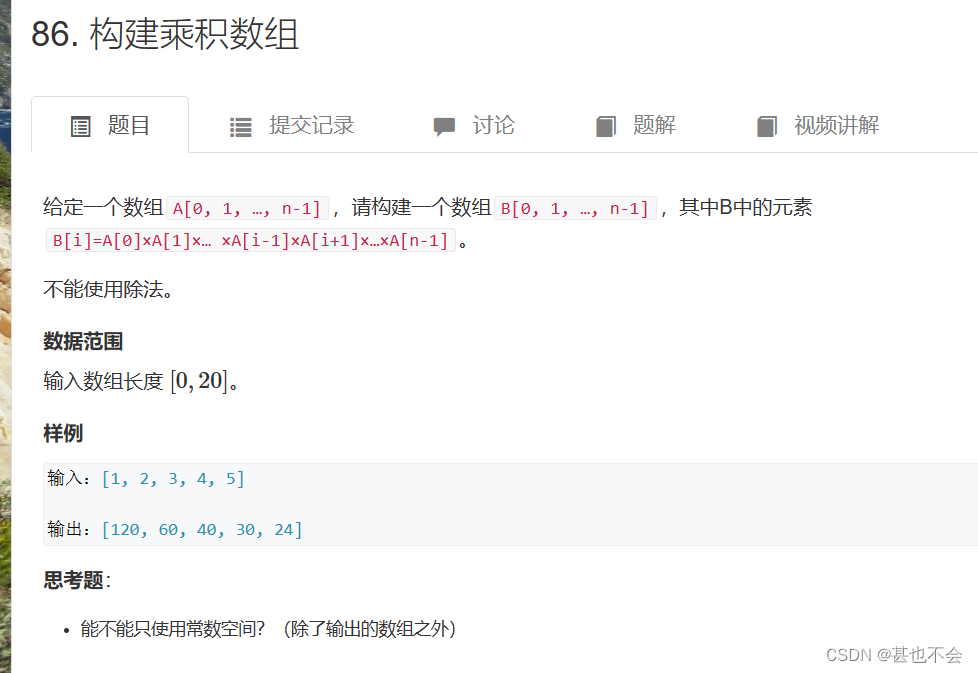
思路分析
-
B[i]主要由 A[0,i] 与A[i+1,n-1] 两个连续部分组成
-
[0,i-1]的计算
B[i-1]=A[0]…*A[i-2]
B[i] =A[0]… *A[i-2] * A[i-1]
观测可知 B[i]=B[i-1]*A[i-1] -
在后半部分计算有着同样的规律,所以我们可以利用两个循环来实现答案的计算
class Solution {
/*分析可知
*1.B[i]的乘积有两部分组成,[0,i-1]与[i+1,r]
*2.我们可以注意到在计算[0,i-1]部分上的B[i]乘积时,可以利用前一个B[i-1]*a[i-1]得到
*3.第二部分倒序计算时,有着相同的规律
*5.所以我们可以利用两次循环来获得结果
*/public int[] multiply(int[] A) {int[] ans=new int[A.length];if(A.length==0)return ans;ans[0]=1;//循环计算第一部分for(int i=1;i<A.length;i++){ans[i]=ans[i-1]*A[i-1];}//计算第二部分循环int tmp=1;//tmp记录前一个循环的值for(int i=A.length-2;i>=0;i--){tmp=tmp*A[i+1];ans[i]*=tmp;}return ans; }
}
day10不用加减乘除的加法
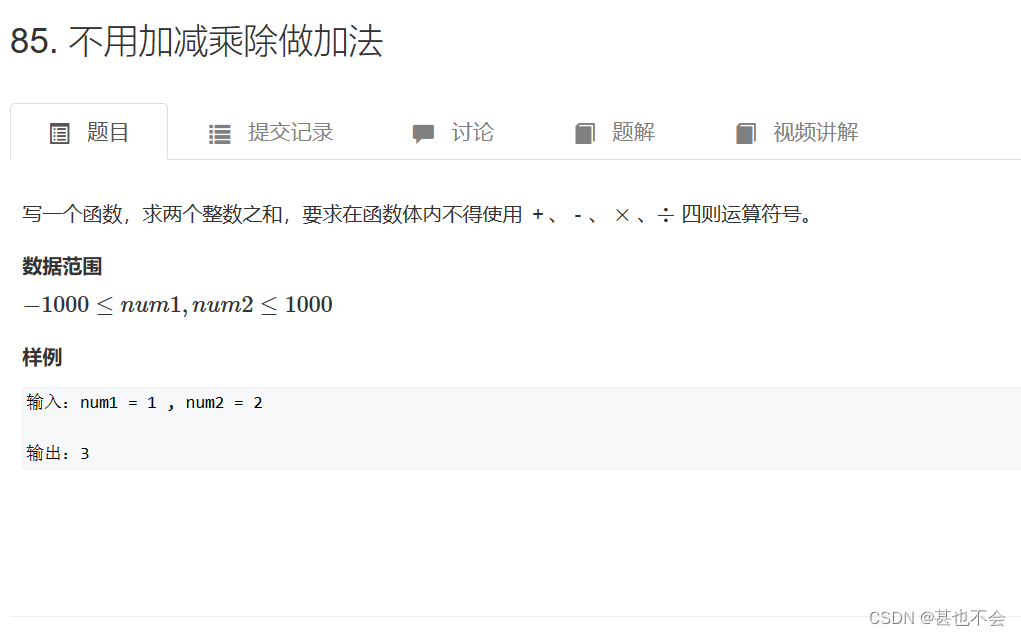
思路分析
- 这里我们利用位运算来求解
- 位运算根据值的不同可以分为4种情况
| a(i) | b(i) | c(i) | c(i+1) |
| ---- | ---- | ---- | ------ |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1| 0 |
| 1 | 1 | 0 | 1 | - 本位:当两个同为1/0时,等于0;否则为1;即 本位 为 a^b
- 进位:两个数同为 1 时 为1 所以 进位 为 a&b
- 我们可以类比10进制,当知道10位数为a,个位数为b—> (a*10+b )
同理,二进制即为:a&b<<1+a^b;
由于不能用加法,我们可以多次循环值进位为0,则此时的 非进位即所求答案
大佬详解
class Solution {public int add(int num1, int num2) {if(num2==0)return num1;return add(num1^num2,(num1&num2)<<1);}
}
day11求1+2…+n
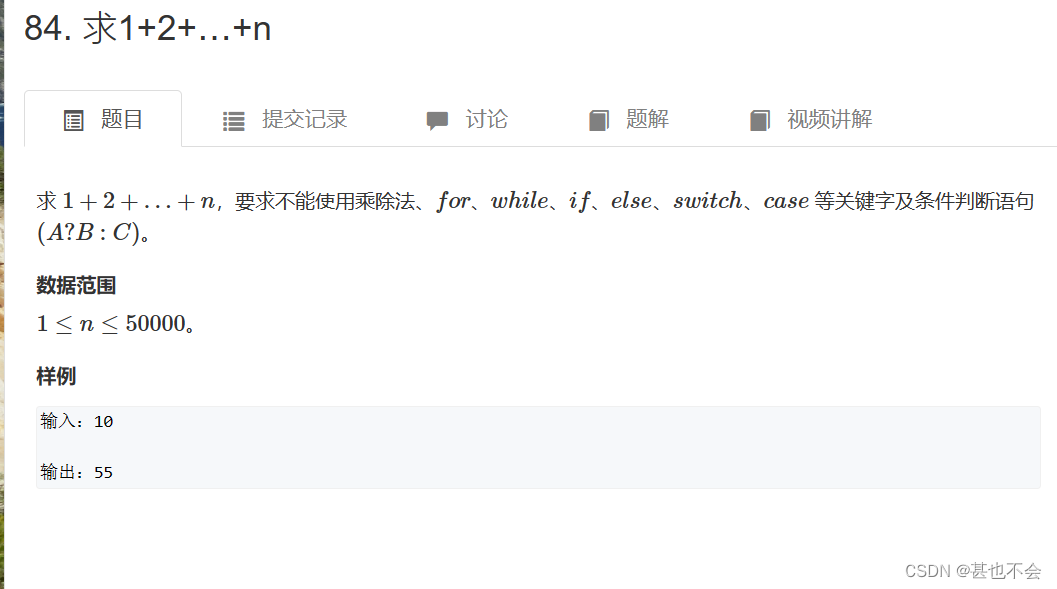
思路分析
- 根据题意不能使用循环和乘除法,所以很容易想到使用递归
- 最小子问题 n=1 return 1;
- 单层逻辑:n+getSum(n-1)
class Solution {public int getSum(int n) {if(n==1)return 1;return n+getSum(n-1);}
}
day11 股票的最大价值
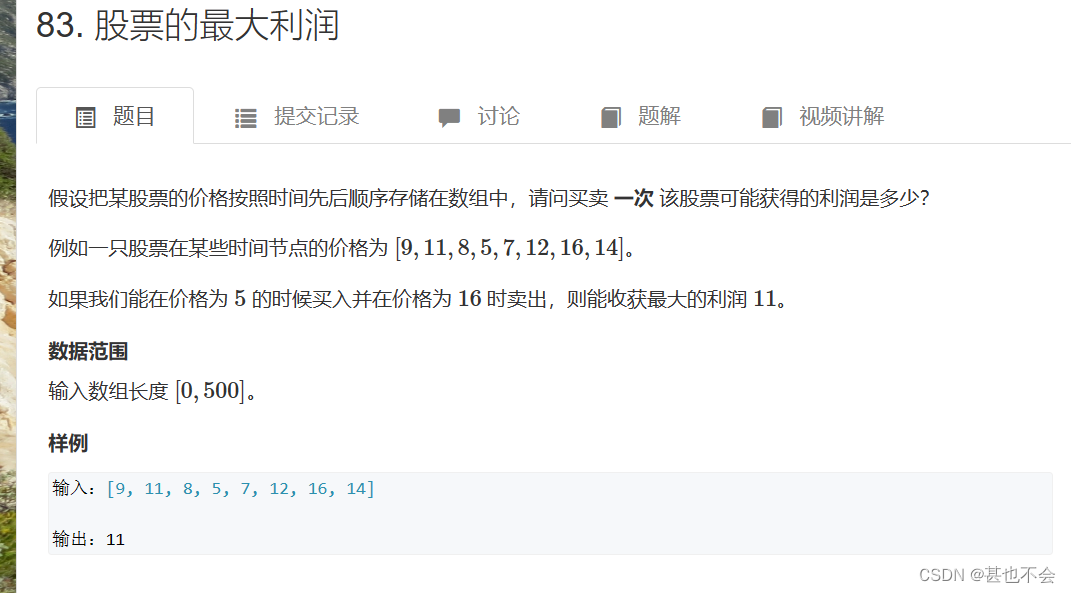
思路分析
- 状态表示
- 状态集合:前i个元素中任选两个元素的所有选法
- 属性:序号后-序号前的最大值
- 状态计算
- 不包含 nums[i] 最大值为 dp[i-1]
- 包含nums[i] 最大值 为 nums[i]-min(前i个元素的最小值)
所以状态转移方程为 dp[i]=Math.max(dp[i-1],nums[i]-min)
day13扑克牌的顺子
day14骰子的点数
day15滑动窗口的最大值
相关文章:

剑指offer打卡
这里写目录标题 day1 二叉树和为某一路径day2复杂链表的复刻day3二叉搜索树与双向链表day4数字排列day5找出出现次数超过一半的次数day6 二进制中1的个数day7 二叉树的最近公共祖先day8 字符串转换为整数day9 构建乘积数组day10不用加减乘除的加法day11求12....nday11 股票的最…...
运维实用脚本整理
运维实用脚本整理 本文脚本仅供参考运维排查问题思路运维排查问题的方法和命令(1)尽可能搞清楚问题的前因后果(2)有谁在?(3)之前发生了什么?(4) 现在在运行的进程是啥?࿰…...
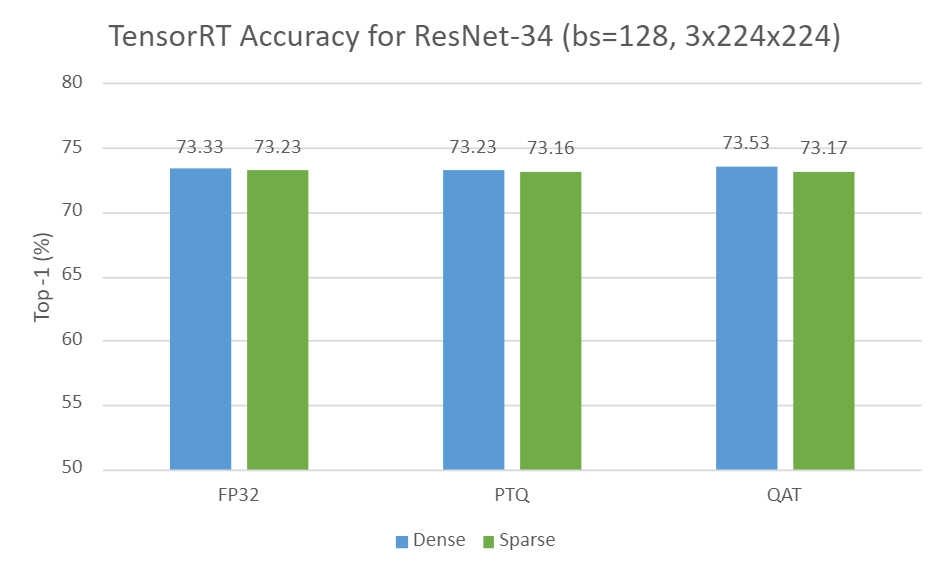
INT8 中的稀疏性:加速的训练工作流程和NVIDIA TensorRT 最佳实践
INT8 中的稀疏性:加速的训练工作流程和NVIDIA TensorRT 最佳实践 文章目录 INT8 中的稀疏性:加速的训练工作流程和NVIDIA TensorRT 最佳实践结构稀疏量化在 TensorRT 中部署稀疏量化模型的工作流程案例研究:ResNet-34要求第 1 步:…...

隧道模式HTTP代理使用代码示例
以下是使用Python实现隧道模式HTTP代理的代码示例: python import socket def handle_client(client_socket): # 接收客户端请求 request client_socket.recv(4096) # 解析请求头,获取目标主机和端口号 host request.split(b\r\n)[1].sp…...

翻筋斗觅食海鸥优化算法-附代码
翻筋斗觅食海鸥优化算法 文章目录 翻筋斗觅食海鸥优化算法1.海鸥优化算法2. 改进海鸥优化算法2.1 非线性参数 A 策略2.2 翻筋斗觅食策略 3.实验结果4.参考文献5.Matlab代码6.python代码 摘要:针对基本海鸥优化算法(SOA)在处理复杂优化问题中存在低精度、…...
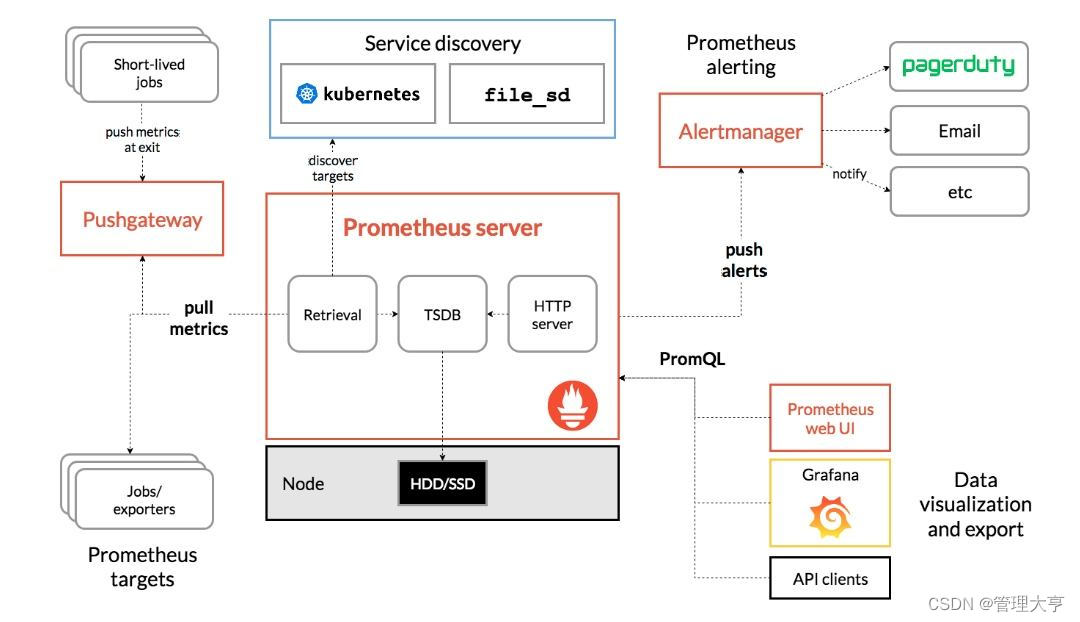
K8S常见应用场景(六)
Kubernetes 是一个可移植的、可扩展的开源平台,用于管理容器化的工作负载和服务,可促进声明式配置和自动化。 Kubernetes 拥有一个庞大且快速增长的生态系统。Kubernetes 的服务、支持和工具广泛可用。 Kubernetes 这个名字源于希腊语,意为“…...

《不抱怨的世界》随记
*不抱怨的世界 * 1.天才只有三件事:我的事,他的事,老天的事。抱怨自己的的人,应该试着学习接纳自己;抱怨他人的人,应该试着把抱怨转成请求;抱怨老天的人么,请试着用祈祷的方式来诉求…...
2.2 利用MyBatis实现CRUD操作
一、准备工作 打开MyBatisDemo项目 二、查询表记录 1、在映射器配置文件里引入结果映射元素 在UserMapper.xml文件里创建结果映射元素 将UserMapper接口里抽象方法上的注解暂时注释掉 运行TestUserMapper测试类里的testFindAll()测试方法,查看结果 2、添加…...
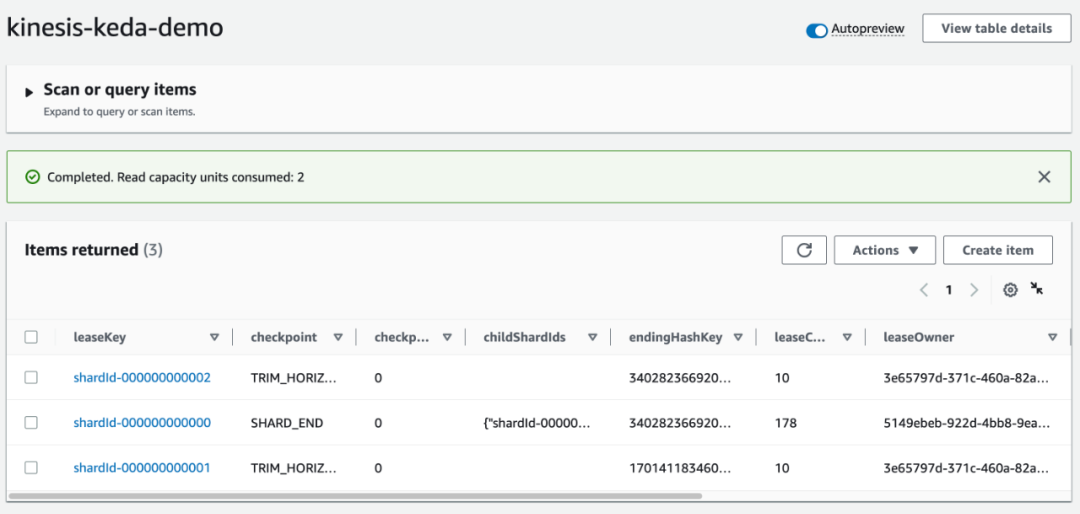
自动缩放Kubernetes上的Kinesis Data Streams应用程序
想要学习如何在Kubernetes上自动缩放您的Kinesis Data Streams消费者应用程序,以便节省成本并提高资源效率吗?本文提供了一个逐步指南,教您如何实现这一目标。 通过利用Kubernetes对Kinesis消费者应用程序进行自动缩放,您可以从其…...

介绍js各种事件
目录 一、点击事件 二、鼠标移动事件 三、键盘事件 四、滚轮事件 五、拖放事件 六、窗口大小改变事件 一、点击事件 点击事件是指当用户单击页面上的某个元素时触发的事件。这是最常见和基础的事件之一,也是Web应用程序中最常用的交互之一。 以下是如何使用…...

Python 将 CSV 分割成多个文件
文章目录 使用 Pandas 在 Python 中创建 CSV 文件在 Python 中将 CSV 文件拆分为多个文件根据行拆分 CSV 文件根据列拆分 CSV 文件 总结 在本文中,我们将学习如何在 Python 中将一个 CSV 文件拆分为多个文件。 我们将使用 Pandas 创建一个 CSV 文件并将其拆分为多个…...
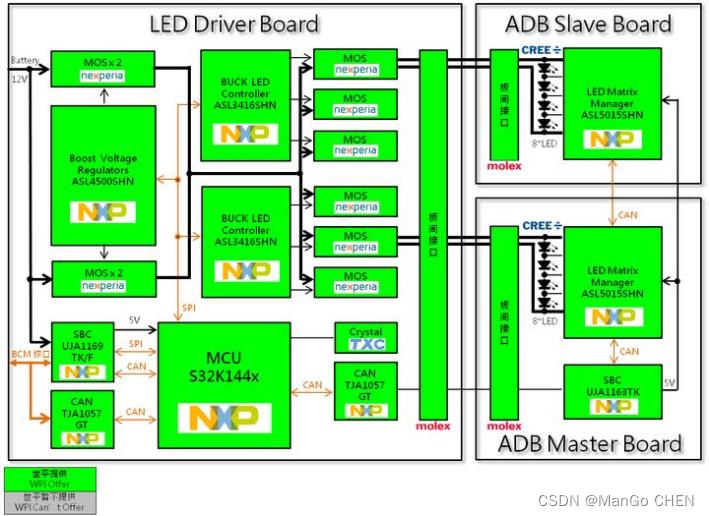
S32K144开发板
目录 一.S32K144开发板概述 二.产品技术和功能规格 三.开发环境 1.S32K144的开发环境主流是这么三种: 2.开发板Demo工程 四.S32K144开发板实物图 五、汽车大灯硬件架构 一.S32K144开发板概述 S32K14…...
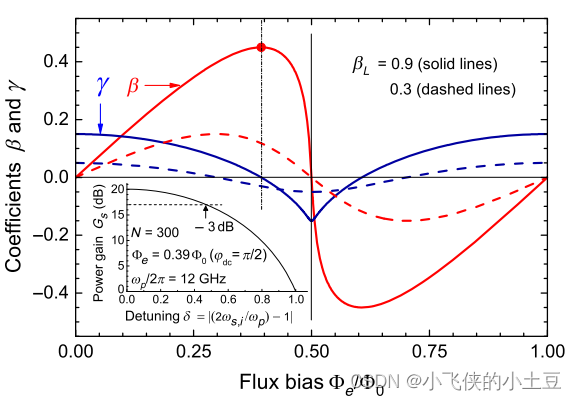
三波混频下的相位失配原理
原理推导 在四波混频情况下,实现零相位失配是一件很困难的事情。因为在四波混频中,相位调制和增益都依赖于相同的参数,即克尔非线性 γ \gamma γ。这个问题可以用嵌入在传输线上的辅助共振元件的复杂色散工程来部分解决。 但是在三波混频中…...

软考A计划-试题模拟含答案解析-卷一
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分享&am…...

Ubuntu下编译运行MicroPython Unix版本
文章目录 github拉取源码更新模块编译运行 github拉取源码 到Github(https://github.com/micropython/micropython)上下载源码 终端输入,如果提示识别不到gh命令,就sudo apt-get install gc安装一下。 再根据提示在终端里登录自己的github账号。 再次…...

实现用QCustomPlot封装的插件,放到绘图软件中可以点击和移动
首先,我们需要在绘图软件中创建一个插件,并将QCustomPlot控件添加到插件中。QCustomPlot是一个功能强大的绘图控件,可以轻松创建各种类型的图表,包括折线图、散点图、柱状图等等。 接下来,我们需要为QCustomPlot控件添加鼠标事件处理函数,以实现点击和移动的功能。QCust…...

【源码解析】Nacos配置热更新的实现原理
使用入门 使用RefreshScopeValue,实现动态刷新 RestController RefreshScope public class TestController {Value("${cls.name}")private String clsName;}使用ConfigurationProperties,通过Autowired注入使用 Data ConfigurationProperti…...

界面组件DevExpress ASP.NET Core v22.2 - UI组件升级
DevExpress ASP.NET Core Controls使用强大的混合方法,结合现代企业Web开发工具所期望的所有功能。该套件通过ASP.NET Razor标记和服务器端ASP.NET Core Web API的生产力和简便性,提供客户端JavaScript的性能和灵活性。ThemeBuilder工具和集成的Material…...

阿里系文生图(PAI+通义)
PAI-Diffusion模型来了!阿里云机器学习团队带您徜徉中文艺术海洋 - 知乎作者:汪诚愚、段忠杰、朱祥茹、黄俊导读近年来,随着海量多模态数据在互联网的爆炸性增长和训练深度学习大模型的算力大幅提升,AI生成内容(AI Gen…...
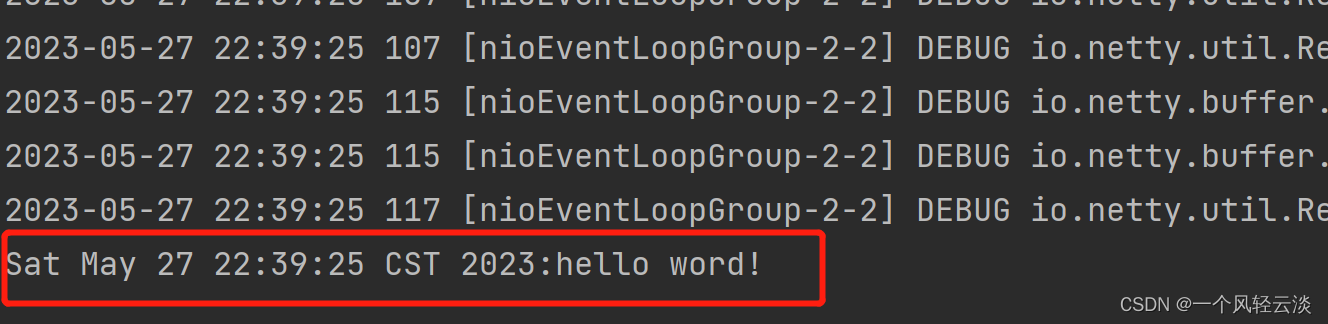
Netty概述及Hello word入门
目录 概述 Netty是什么 Netty的地位 Netty的优势 HelloWord入门程序 目标 pom依赖 服务器端 客户端 运行结果 入门把握理解 概述 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable hi…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
