信息论与编码 SCUEC DDDD 期末复习
1.证明熵的可加性

2.假设一帧视频图像可以认为是由3*10的五次方个像素组成(每像素均独立变化),如果每个像素可取128个不同的等概率亮度表示。请计算出每帧图像含多少信息量?若有一口述者在约12000个汉字的字汇中选400个字来口述此电视图像,试问口述者描述此图像所需要的信息量是多少(假设汉字是等概率独立分布)?若要恰当地描述此图像,口述者在口述中至少需要用多少汉字?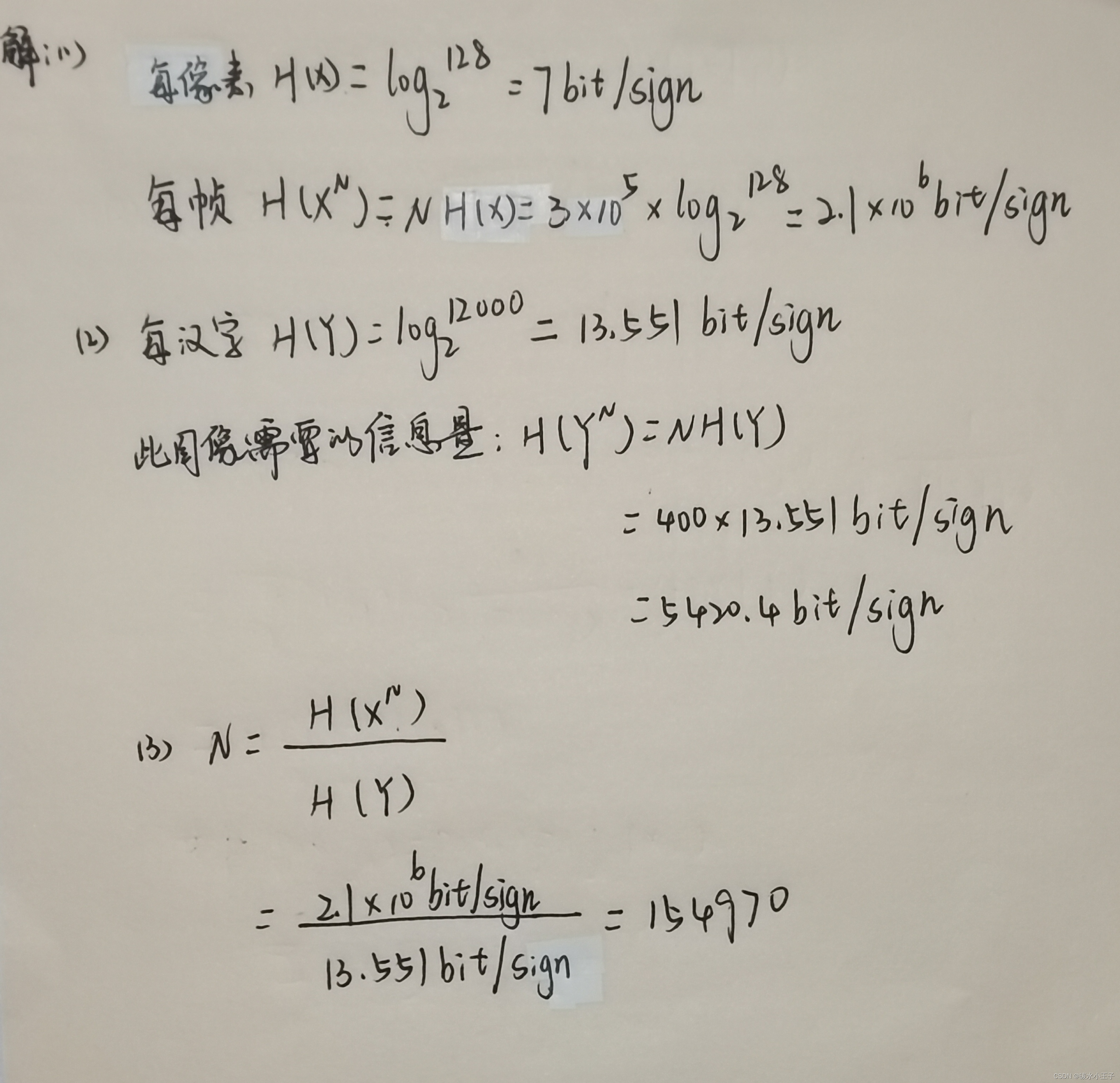
3.信源:产生要传输的消息。
4.信源编码:对信源输出进行变化(消除冗余,压缩),提高信息传输的有效性。
5.信道编码:对信源编码输出变换(加入冗余),提高抗干扰能力,提高信息传输的可靠性。
6.加密编码:提高传输的安全性。
7.信道:信号传输的介质。
8.信宿:接受信源传输的消息。
9.无失真信源编码定理(香农第一定理)
如果信源编码码率 R (编码后传送信源符号所需比特数)不小于信源的熵 H ( X ),就存在无失真编码,反之不存在无失真编码。
10.有噪信道编码定理(香农第二定理)
如果信息传输速率小于信道容量,则总可以找到一种编码方式使得当编码序列足够长时传输差错任意小。反之不存在使差错任意小的编码。
11.限失真信源编码定理(香农第三定理)
只要码字足够长,总可以找到一种编码,使得当编码码率 R > R ( D )时,码的平均失真 D ;反之不存在平均失真 D 的编码。在允许一定失真度 D 的情况下,信源输出的信息率可以压缩到 R ( D )。
R ( D )称为信息率失真函数,是满足失真准则(平均失真 D )下,每个信源符号所需最小编码比特数。
12.平均错误概率不仅与信道本身的统计特性有关,还与编码方法和译码准则有关。
13.事件发生的概率越小,不确定性就越大。概率等于1的必然事件,不存在不确定性。
14.如果知道事件 Xi 已发生,则事件包含的自信息定义为:
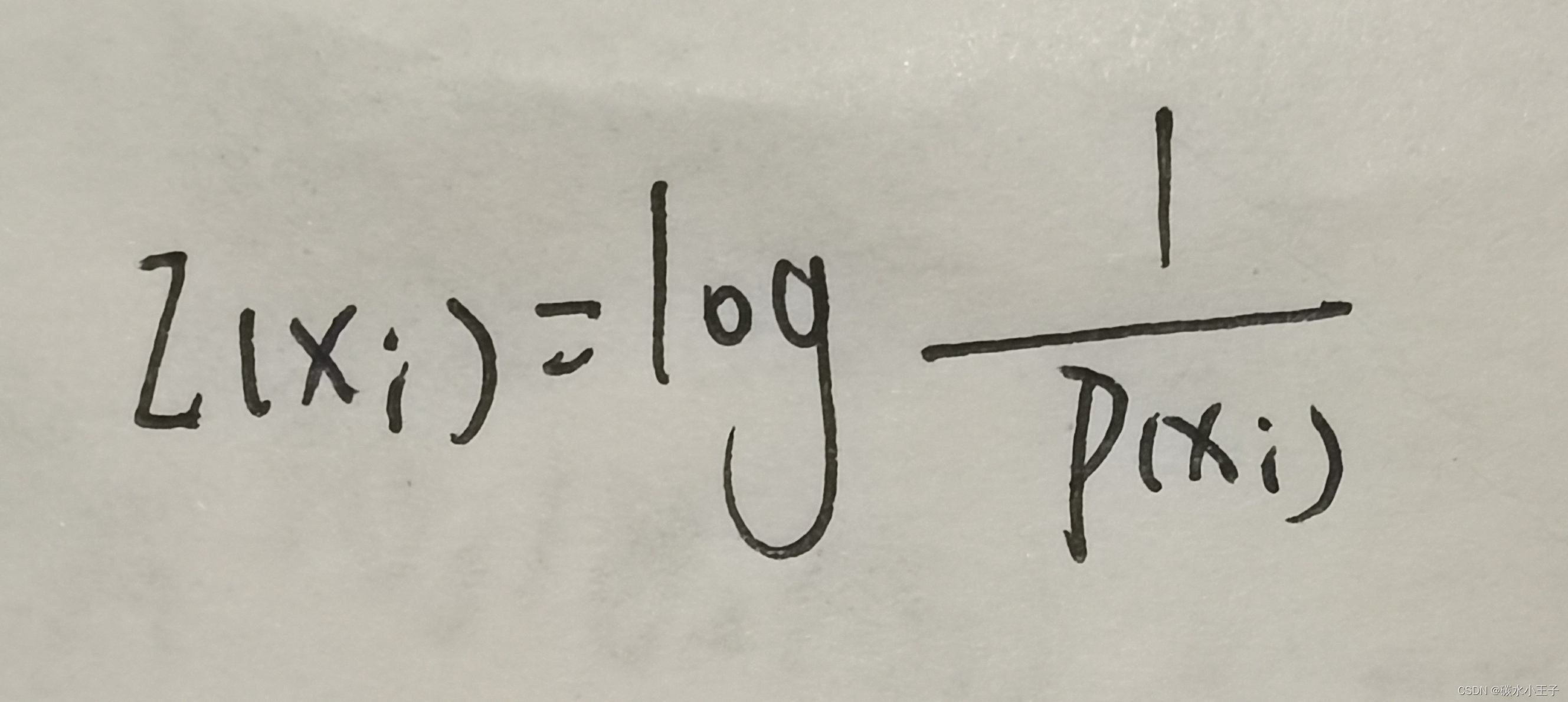
15.自信息的含义
当事件 Xi 发生以前表示事件 Xi 发生的不确定性;
当事件 Xi 发生以后表示事件 X 所包含的信息量。
16.信源自信息量为非负值;当事件发生概率为1时,自信息量为0;当事件发生概率为0时,自信息量为无穷大;自信息量是事件发生概率的单调递减函数。
5.联合自信息量
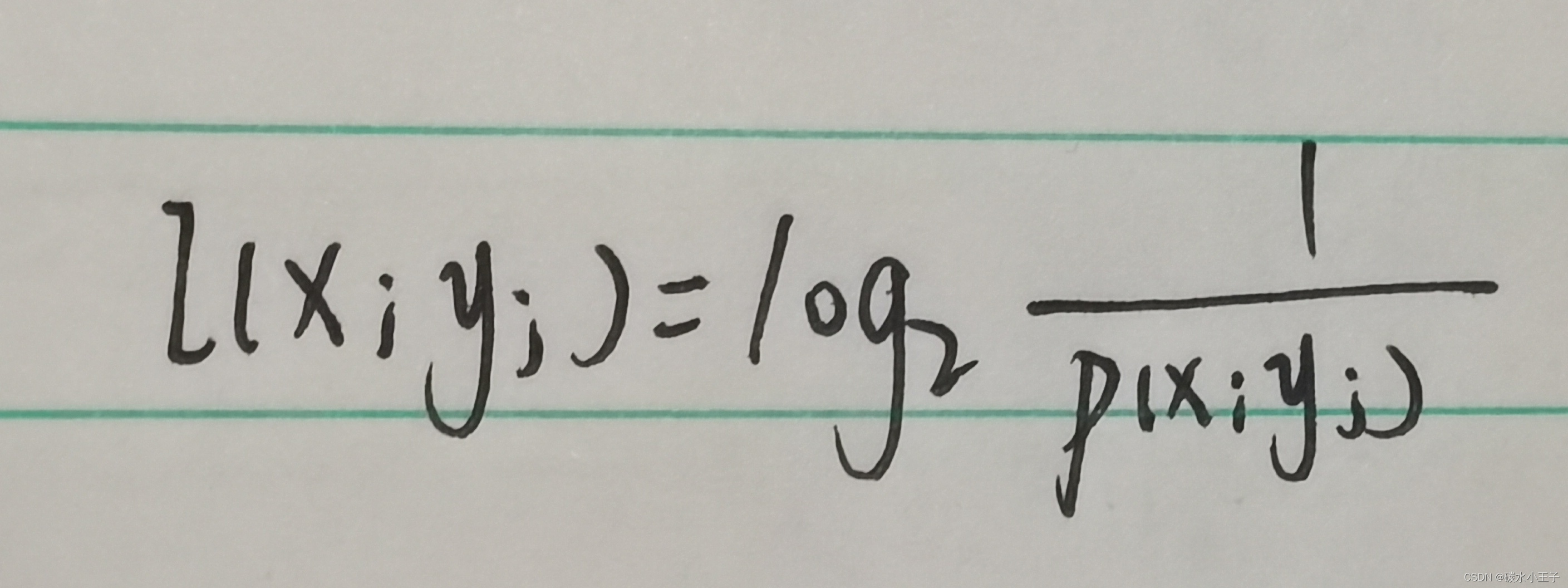 当 X 和 Y 相互独立时:
当 X 和 Y 相互独立时:
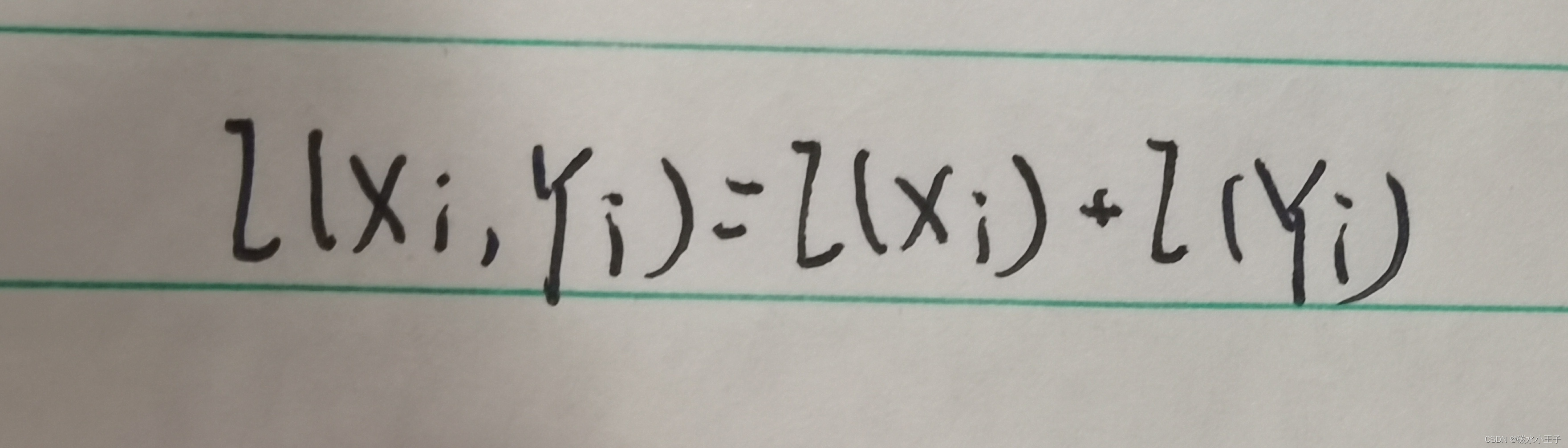
6.关于信道容量与信息的可靠传输
有噪信道编码定理(香农第二定理)是信道编码的理论基础,其内容是:如果信息传输速率小于信道容量,则总可找到一种编码方式使得当编码序列足够长时传输差错任意小,反之不存在使差错任意小的编码。
7.信息率失真理论(数据压缩的理论基础)
限失真信源编码定理(香农第三定理)的是有损压缩编码的理论基础,其内容是:只要码字足够长,总可找到一种编码,使得当信源编码的码率> R ( D )时,码的平均失真 D ;反之,如果信源编码的码率< R ( D ),就不存在平均失真 D 的编码。可以简述为:在允许一定失真度 D 的情况下,信源输出的信息率可压缩到 R ( D )
R ( D )称为信息率失真函数,是满足失真准则(平均失真 D )下,每信源符号所需最小编码比特数。
8.
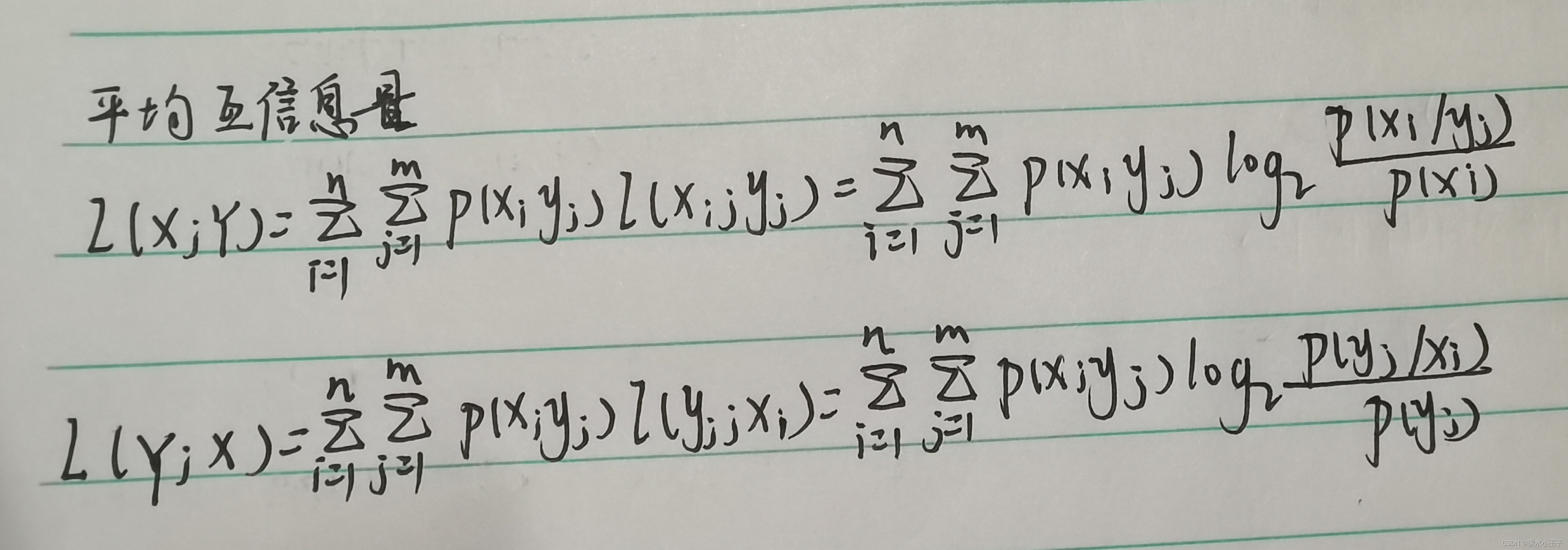
9.熵的基本性质和定理

相关文章:

信息论与编码 SCUEC DDDD 期末复习
1.证明熵的可加性 2.假设一帧视频图像可以认为是由3*10的五次方个像素组成(每像素均独立变化),如果每个像素可取128个不同的等概率亮度表示。请计算出每帧图像含多少信息量?若有一口述者在约12000个汉字的字汇中选400个字来口述此…...
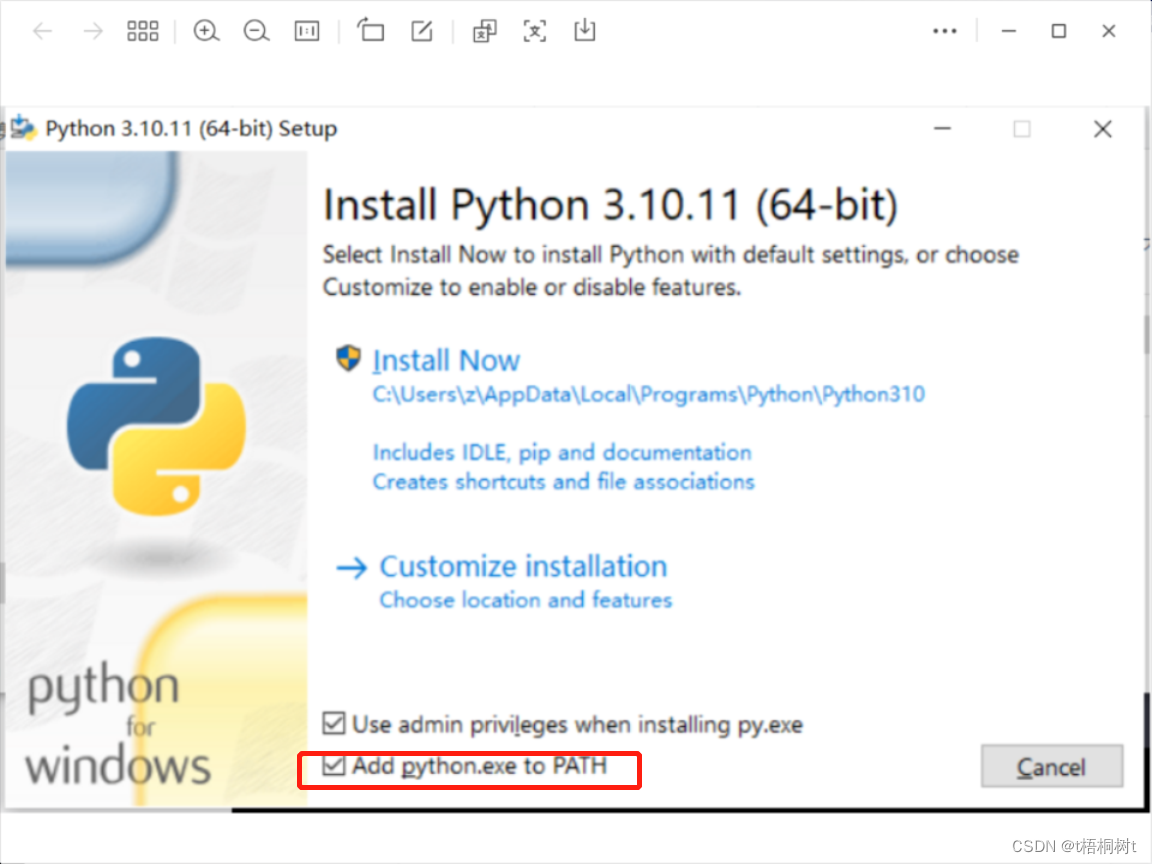
windows安装python开发环境
最近因工作需要,要学习一下python,所以先安装一下python的开发环境,比较简单 下载和安装Python 首先,在浏览器中打开Python的官方网站(https://www.python.org/downloads/) 然后,从该网站下载与你的操…...

java idea常用的快捷方式
文章目录 java idea常用的快捷方式快速复制选多行改变代码格式化 快速代码编辑psvmsout5.forarr.for快速死循环快速补全代码当方法还没创建的时候抽取具有一定功能的代码变成方法 java idea常用的快捷方式 快速复制 c t r l d \color{red}{ctrld} ctrld 选多行改变 A l t 鼠…...

lwIP 开发指南
目录 lwIP 初探TCP/IP 协议栈是什么TCP/IP 协议栈架构TCP/IP 协议栈的封包和拆包 lwIP 简介lwIP 源码下载lwIP 文件说明 MAC 内核简介PHY 芯片介绍YT8512C 简介LAN8720A 简介 以太网接入MCU 方案软件TCP/IP 协议栈以太网接入方案硬件TCP/IP 协议栈以太网接入方案 lwIP 无操作系…...

RabbitMQ消息属性详解
content-type属性 如同各种标准化的HTTP规范,content-type传输消息体的MIME类型。例如,如果你的应用程序正在发送JSON序列化的数据值,那么将content-type属性设置为application/json将允许尚待开发的消费者应用程序在收到消息时检查消息类型…...

shader 混合模式
在所有着色器执行完毕,所有纹理都被应用,所有像素准备被呈现到屏幕之后,使用Blend命令来操作这些像素进行混合。 3.2 blend的语法 BlendOff:关闭blend混合(默认值) BlendSrcFactor DstFactor :配置并启动混…...

【大数据工具】Hive 安装
Hive 环境搭建与基本使用 Hive 安装包下载地址:https://dlcdn.apache.org/hive/ 注:安装 Hive 前要先安装好 MySQL 1. MySQL 安装 MySQL 安装包下载地址:https://dev.mysql.com/downloads/mysql/archives/community/MySQL%20::%20Downloa…...

Android9.0 iptables用INetd实现app某个时间段禁止上网的功能实现
1.前言 在9.0的系统rom定制化开发中,在system中netd网络这块的产品需要中,会要求设置app某个时间段禁止上网的功能,liunx中iptables命令也是比较重要的,接下来就来在INetd这块实现app某个时间段禁止上网的的相关功能,就是在系统中只能允许某个app某个时间段禁止上网,就是…...

webpack.config.js基础配置(五大核心属性)
在上一节webpack零基础入门中我们在安装完webpack 和 webpack-cli依赖之后,直接通过npx webpack ./src/main.js --modedevelopment的方式对src下的js文件进行了打包。 其中的 ./src/main.js: 指定 Webpack 从 main.js 文件开始打包,不但会打包 main.js&a…...
【2023 B卷|200分】)
【华为OD机试】阿里巴巴找黄金宝箱(IV)【2023 B卷|200分】
【华为OD机试】-真题 !!点这里!! 【华为OD机试】真题考点分类 !!点这里 !! 题目描述 一贫如洗的樵夫阿里巴巴在去砍柴的路上,无意中发现了强盗集团的藏宝地, 藏宝地有编号从0-N的箱子,每个箱子上面有一个数字,箱子排列成一个环, 编号最大的箱子的下一个是编号为0的箱…...

Qt6 C++基础入门2 文件结构与信号和槽
目录 标准文件结构widget.hwidget.cppmain.cpppro 文件 信号与槽自定义信号connect 的两种方式 标准文件结构 widget.h widget 对象的头文件 一般会直接在头文件导入所有后续在 cpp 文件内用到的类,所以 include 基本都会写在这里 // 头文件标志起始 #ifndef WID…...
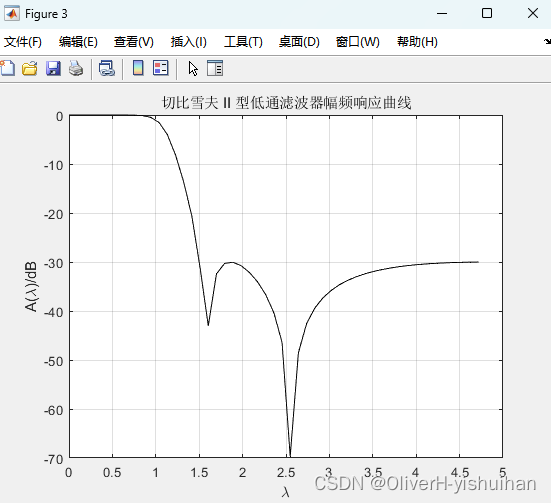
常用模拟低通滤波器的设计——契比雪夫II型滤波器
常用模拟低通滤波器的设计——契比雪夫II型滤波器 切比雪夫 II 型滤波器的振幅平方函数为: 式中,为有效带通截止频率, 是与通带波纹有关的参量, 大,波纹大,; 为 N 阶契比雪夫多项式。 在 Matl…...

SSM 如何使用 Redis 实现缓存?
SSM 如何使用 Redis 实现缓存? Redis 是一个高性能的非关系型数据库,它支持多种数据结构和多种操作,可以用于缓存、队列、计数器等场景。在 SSM(Spring Spring MVC MyBatis)开发中,Redis 可以用来实现数…...

uin-app如何获取微信昵称和头像的博客
在很多应用中都会使用到微信登录功能,这样可以方便用户快速地完成注册、登录等操作。本文将介绍如何通过uin-app获取微信用户的昵称和头像信息。 第一步:准备开发环境 首先,需要下载并安装QQ精简版开发工具(uin-app)…...

第六十七天学习记录:对陈正冲编著《C 语言深度解剖》中关于变量命名规则的学习
最近开始在阅读陈正冲编著的《C 语言深度解剖》,还没读到十分之一就感觉收获颇多。其中印象比较深刻的是其中的变量的命名规则。 里面提到的不允许使用拼音正是我有时候会犯的错。 因为在以往的工作中,偶尔会遇到时间紧迫的情况。 而对于新增加的变量不知…...

matlab 计算点云的线性指数
目录 一、算法原理二、代码实现三、结果展示一、算法原理 选取当前点 p i ( x , y , z ) p_{i}(x,y,z) p<...
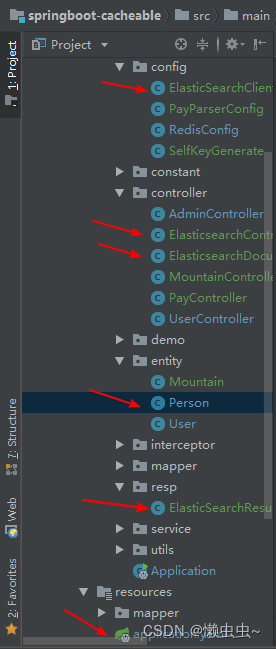
SpringBoot集成ElasticSearch
文章目录 前言一、ElasticSearch本地环境搭建二、SpringBoot整合ElasticSearch1.pom中引入ES依赖2.application.yaml配置elasticsearch3.ElasticSearchClientConnect连接ES客户端工具类4.ElasticSearchResult封装响应结果5.Person实体类6.Person实体类7.ElasticsearchControlle…...

分治入门+例题
目录 🥇2.3.2 合并排序 🥇2.3.3 快速排序 🌼P1010 [NOIP1998 普及组] 幂次方 🌳总结 形象点,分治正如“凡治众如治寡,分数是也”,管理少数几个人,即可统领全军 本质ÿ…...
剑指offer打卡
这里写目录标题 day1 二叉树和为某一路径day2复杂链表的复刻day3二叉搜索树与双向链表day4数字排列day5找出出现次数超过一半的次数day6 二进制中1的个数day7 二叉树的最近公共祖先day8 字符串转换为整数day9 构建乘积数组day10不用加减乘除的加法day11求12....nday11 股票的最…...
运维实用脚本整理
运维实用脚本整理 本文脚本仅供参考运维排查问题思路运维排查问题的方法和命令(1)尽可能搞清楚问题的前因后果(2)有谁在?(3)之前发生了什么?(4) 现在在运行的进程是啥?࿰…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
