哈希表题目:矩阵置零
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 进阶
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
- 解法三
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:矩阵置零
出处:73. 矩阵置零
难度
3 级
题目描述
要求
给定一个 m×n\texttt{m} \times \texttt{n}m×n 的矩阵,如果一个元素为 0\texttt{0}0,则将其所在行和列的所有元素都设为 0\texttt{0}0。
请使用原地算法。
示例
示例 1:
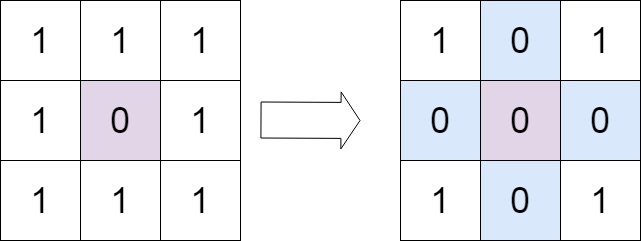
输入:matrix=[[1,1,1],[1,0,1],[1,1,1]]\texttt{matrix = [[1,1,1],[1,0,1],[1,1,1]]}matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]\texttt{[[1,0,1],[0,0,0],[1,0,1]]}[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
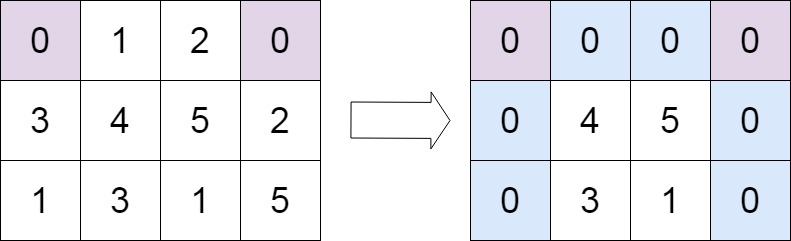
输入:matrix=[[0,1,2,0],[3,4,5,2],[1,3,1,5]]\texttt{matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]}matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]\texttt{[[0,0,0,0],[0,4,5,0],[0,3,1,0]]}[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
数据范围
- m=matrix.length\texttt{m} = \texttt{matrix.length}m=matrix.length
- n=matrix[0].length\texttt{n} = \texttt{matrix[0].length}n=matrix[0].length
- 1≤m,n≤200\texttt{1} \le \texttt{m, n} \le \texttt{200}1≤m, n≤200
- -231≤matrix[i][j]≤231−1\texttt{-2}^\texttt{31} \le \texttt{matrix[i][j]} \le \texttt{2}^\texttt{31} - \texttt{1}-231≤matrix[i][j]≤231−1
进阶
- 一个直观的解决方案是使用 O(mn)\texttt{O(mn)}O(mn) 的额外空间,但这并不是一个好的解决方案。
- 一个简单的改进方案是使用 O(m+n)\texttt{O(m + n)}O(m + n) 的额外空间,但这仍然不是最好的解决方案。
- 你能想出一个仅使用常量空间的解决方案吗?
解法一
思路和算法
最直观的做法是找到矩阵中所有等于 000 的元素,对于每个元素 000,将其所在行和列的所有元素置零。
如果直接在原矩阵中将元素置零,则无法判断等于 000 的元素是原始值等于 000 还是被置零,因此需要创建辅助矩阵,辅助矩阵和原矩阵的大小相同,辅助矩阵中的每个元素表示原矩阵中的该元素是否置零。
遍历原矩阵,对于原矩阵中每个等于 000 的元素,将辅助矩阵中相应位置的相同行和相同列的元素都设为置零。然后再次遍历原矩阵和辅助矩阵,对于辅助矩阵中置零的位置,将原矩阵中相应位置的元素置零。
代码
class Solution {public void setZeroes(int[][] matrix) {int m = matrix.length, n = matrix[0].length;boolean[][] zero = new boolean[m][n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == 0) {for (int k = 0; k < n; k++) {zero[i][k] = true;}for (int k = 0; k < m; k++) {zero[k][j] = true;}}}}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (zero[i][j]) {matrix[i][j] = 0;}}}}
}
复杂度分析
-
时间复杂度:O(mn(m+n))O(mn(m + n))O(mn(m+n)),其中 mmm 和 nnn 分别是矩阵 matrix\textit{matrix}matrix 的行数和列数。需要遍历矩阵两次,第一次遍历需要将元素 000 所在行和列的所有元素标为置零,每个元素需要 O(m+n)O(m + n)O(m+n) 的处理时间,第二次遍历将矩阵中的标为置零的元素置零,每个元素需要 O(1)O(1)O(1) 的处理时间,因此总时间复杂度是 O(mn(m+n))O(mn(m + n))O(mn(m+n))。
-
空间复杂度:O(mn)O(mn)O(mn),其中 mmm 和 nnn 分别是矩阵 matrix\textit{matrix}matrix 的行数和列数。需要创建和原矩阵大小相同的辅助矩阵记录原矩阵中的每个元素是否置零。
解法二
思路和算法
解法一的时间复杂度和空间复杂度都较高,可以优化。
由于矩阵中每个元素 000 所在行和列的所有元素需要置零,因此只需要记录矩阵的每一行和每一列是否需要置零即可。
创建两个哈希表分别记录矩阵的每一行和每一列是否需要置零,遍历矩阵一次,对于每个等于 000 的元素,在两个哈希表中分别记录其所在行和列需要置零,遍历结束之后即可得到所有需要置零的行和列。然后再次遍历矩阵,对于每个元素,如果两个哈希表中至少有一个哈希表记录了该元素所在的行或列需要置零,则将该元素置零。
实现方面,可以用两个数组分别记录矩阵的每一行和每一列是否需要置零。
代码
class Solution {public void setZeroes(int[][] matrix) {int m = matrix.length, n = matrix[0].length;boolean[] rows = new boolean[m];boolean[] columns = new boolean[n];for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (matrix[i][j] == 0) {rows[i] = true;columns[j] = true;}}}for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {if (rows[i] || columns[j]) {matrix[i][j] = 0;}}}}
}
复杂度分析
-
时间复杂度:O(mn)O(mn)O(mn),其中 mmm 和 nnn 分别是矩阵 matrix\textit{matrix}matrix 的行数和列数。需要遍历矩阵两次,第一次遍历需要将元素 000 所在行和列在两个哈希表中记录,每个元素需要 O(1)O(1)O(1) 的处理时间,第二次遍历将矩阵中的标为置零的元素置零,每个元素需要 O(1)O(1)O(1) 的处理时间,因此总时间复杂度是 O(mn)O(mn)O(mn)。
-
空间复杂度:O(m+n)O(m + n)O(m+n),其中 mmm 和 nnn 分别是矩阵 matrix\textit{matrix}matrix 的行数和列数。需要创建两个哈希表(或数组)分别记录矩阵的每一行和每一列是否需要置零,各需要 O(m)O(m)O(m) 和 O(n)O(n)O(n) 的空间。
解法三
思路和算法
解法二仍需要 O(m+n)O(m + n)O(m+n) 的额外空间。如果要将空间复杂度降低到 O(1)O(1)O(1),必须在矩阵内部记录每一行和每一列是否需要置零。
在矩阵内部记录置零信息,可以使用第 000 行和第 000 列记录。第 000 行的一个元素如果是 000,则表示该元素所在列需要置零;第 000 列的一个元素如果是 000,则表示该元素所在行需要置零。
如果直接修改矩阵的第 000 行和第 000 列的元素,则无法记录矩阵的第 000 行和第 000 列是否需要置零,因此需要使用两个变量分别记录矩阵的第 000 行和第 000 列是否需要置零。
矩阵置零的完整过程如下。
-
遍历矩阵的第 000 行和第 000 列,记录矩阵的第 000 行和第 000 列是否需要置零。
-
遍历矩阵的其余元素(指除了第 000 行和第 000 列的全部元素,下同),对于每个等于 000 的元素,将其所在行的第 000 列的元素和所在列的第 000 行的元素置零。
-
再次遍历矩阵的其余元素,对于每个元素,如果一个元素所在的行或列需要置零,则将该元素置零。
-
如果矩阵的第 000 行需要置零,则将矩阵的第 000 行元素全部置零;如果矩阵的第 000 列需要置零,则将矩阵的第 000 列元素全部置零。
如果矩阵的第 000 行或第 000 列的一个元素原本就是 000,则该元素所在行和列需要置零,上述解法同样适用于该情况。
代码
class Solution {public void setZeroes(int[][] matrix) {int m = matrix.length, n = matrix[0].length;boolean rowZero = false, columnZero = false;for (int j = 0; j < n; j++) {if (matrix[0][j] == 0) {rowZero = true;break;}}for (int i = 0; i < m; i++) {if (matrix[i][0] == 0) {columnZero = true;break;}}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (matrix[i][j] == 0) {matrix[i][0] = 0;matrix[0][j] = 0;}}}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (matrix[i][0] == 0 || matrix[0][j] == 0) {matrix[i][j] = 0;}}}if (rowZero) {for (int j = 0; j < n; j++) {matrix[0][j] = 0;}}if (columnZero) {for (int i = 0; i < m; i++) {matrix[i][0] = 0;}}}
}
复杂度分析
-
时间复杂度:O(mn)O(mn)O(mn),其中 mmm 和 nnn 分别是矩阵 matrix\textit{matrix}matrix 的行数和列数。最多需要遍历矩阵中的每个元素两次。
-
空间复杂度:O(1)O(1)O(1)。
相关文章:

哈希表题目:矩阵置零
文章目录题目标题和出处难度题目描述要求示例数据范围进阶解法一思路和算法代码复杂度分析解法二思路和算法代码复杂度分析解法三思路和算法代码复杂度分析题目 标题和出处 标题:矩阵置零 出处:73. 矩阵置零 难度 3 级 题目描述 要求 给定一个 m…...
HTTP API自动化测试从手工到平台的演变
不管是 Web 系统,还是移动 APP,前后端逻辑的分离设计已经是常态化,相互之间通过 API 调用进行数据交互。在基于 API 约定的开发模式下,如何加速请求 / 响应的 API 测试,让研发人员及早参与到调试中来呢?既然…...

【从零开始学C语言】知识总结一:C语言的基本知识汇总
C语言期末知识点总结 C语言期末试题(附答案)选择题编程题 2022C语言知识点大全【详细、必备】 C语言期末大作业-学生成绩管理系统(完整源码设计报告) C语言期末作业(15个)-货物管理系统、歌曲信息管理系…...

CAD二次开发 添加按钮Ribbon
这篇文章是教大家怎样子创建自己的Ribbon按钮界面(如下图),以下示例代码在CAD2020中运行实现。 背景 创建一个属于自己的Ribbon按钮(如下图) 理解Ribbon、Panel、Tab的关系(如下图)ÿ…...

[RK3568 Android12] 添加自定义启动脚本
1:定义添加的脚本 比如为displayn2k.sh #!/system/bin/sh log "displayn2k.sh begin running" sleep 5 log "displayn2k.sh sleep 8" sleep 5 log "================sleep finished==========================" #remount /system/bin/mount -o …...

API 体系构建
前言 API 是模块或者子系统之间交互的接口定义。好的系统架构离不开好的 API 设计,而一个设计不够完善的 API 则注定会导致系统的后续发展和维护非常困难。在关键环节制定明确的 API 规范有助于 Service 对内提高产品间互通的效率,对外提供一致的使用体…...

RMPE: Regional Multi-Person Pose Estimation (AlphaPose)阅读笔记
区域多人姿态估计 ICCV 2017 论文链接 代码链接 摘要: 野外多人姿态估计具有挑战性。sota人体检测器不可避免存在定位和识别误差,这些误差可能导致依赖人体检测器的单人姿态估计器(SPPE)的失败。本文提出了一种新的区域多人姿态估…...

2月16日昆明面试经历部分考题
2月16日昆明面试部分考题 1.说说em和rem的区别?rpx呢? rem是相对于根元素(HTML)进行计算,而em是相对于当前元素或父元素的字体大小,如果当前文本的字体尺寸没有设置,则相对于浏览器的默认字体…...

ARC140D One to One
ARC140D One to One 题目大意 对于一个长度为nnn的整数序列X(x1,x2,…xn)X(x_1,x_2,\dots x_n)X(x1,x2,…xn),每个元素都在111到nnn之间,令f(X)f(X)f(X)表示以下问题的答案: 有一个nnn个顶点nnn条边的无向图(可能有重边和…...

联合身份验证与Cognito
Hello大家好,我们接下来讨论AWS联合身份验证的内容。 AWS联合身份验证 对于考试,联合身份验证部分是一块非常重要的内容。那什么是联合身份验证,它是做什么用的呢? 联合身份验证,是用来允许AWS外部用户,如…...

day18_常用API之String类丶Object类
String概述 java.lang.String 类代表字符串,String类定义的变量可以用于指向字符串对象,同时String类提供了很多操作字符串的功能,我们可以直接使用。Java 程序中的所有字符串文字(例如“abc”)都为此类的对象 特点:St…...

OSG三维渲染引擎编程学习之五十五:“第五章:OSG场景渲染” 之 “5.13 一维纹理”
目录 第五章 OSG场景渲染 5.13 一维纹理 5.13.1 一维纹理介绍 5.13.2 一维纹理示例 第五章 OSG场景渲染 OSG存在场景树和渲染树,“场景数”的构建在第三章“OSG场景组织”已详细阐明,本章开始...
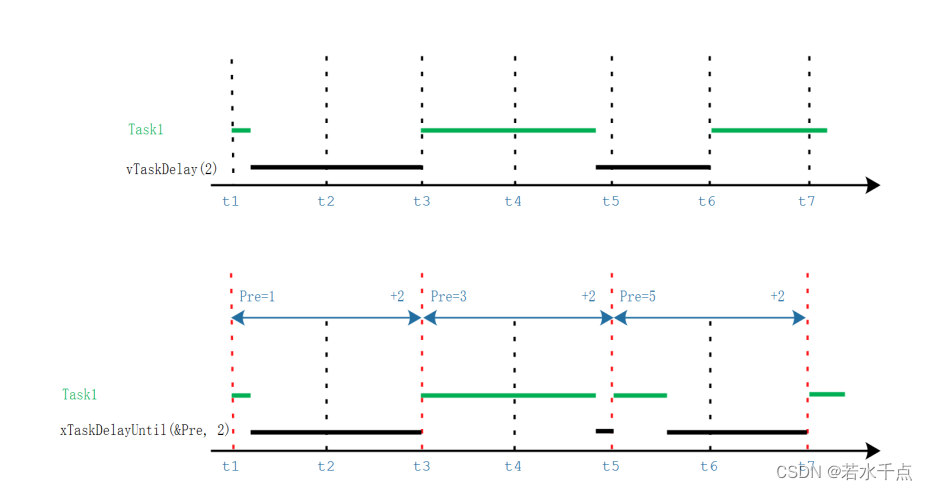
RTOS随笔之FreeRTOS启动与同步方法
RTOS启动与同步机制RTOS启动任务切换场景任务同步机制队列信号量事件组任务通知任务延时RTOS启动 FreeRTOS在任务创建完成后调用函数vTaskStartScheduler()启动任务调度器。 vTaskStartScheduler()任务启动函数详解 void vTaskStartScheduler( void ) {BaseType_t xReturn;xR…...
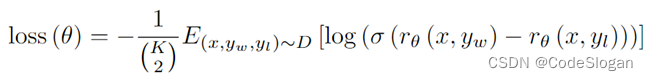
【AI/NLP】InstructGPT数据标注问题
文章目录1 背景介绍2 标记员筛选2.1 标记员筛选标准3 数据集及其标注3.1 预训练3.2 微调3.2.1 SFT-demonstration data3.2.2 RM-comparison data3.3 数据集大小4 模型实现1 背景介绍 ChatGPT的训练过程与InstructGPT相近,大致分为三步: SFT:…...
三次握手和四次挥手
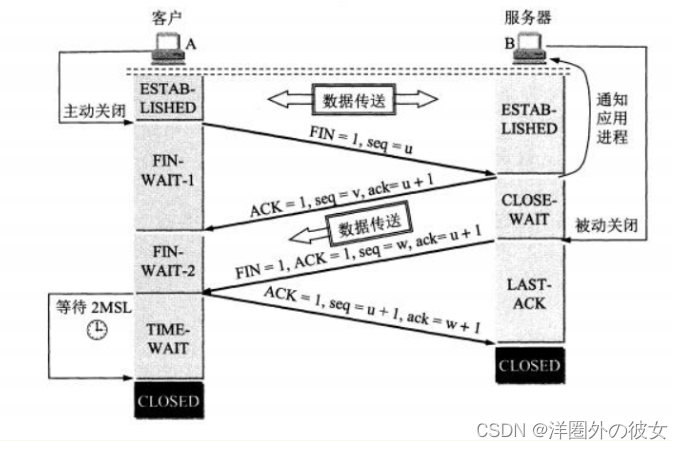
文章目录TCP三次握手为什么要三次握手三次握手可以携带数据吗?三次握手失败,服务端会如何处理?ISN代表什么,意义,何要动态随机什么是半连接队列第2次握手传回了ACK,为什么还要传回SYN?为什么要四次挥手TCP…...
Jmeter常用断言之响应断言详解
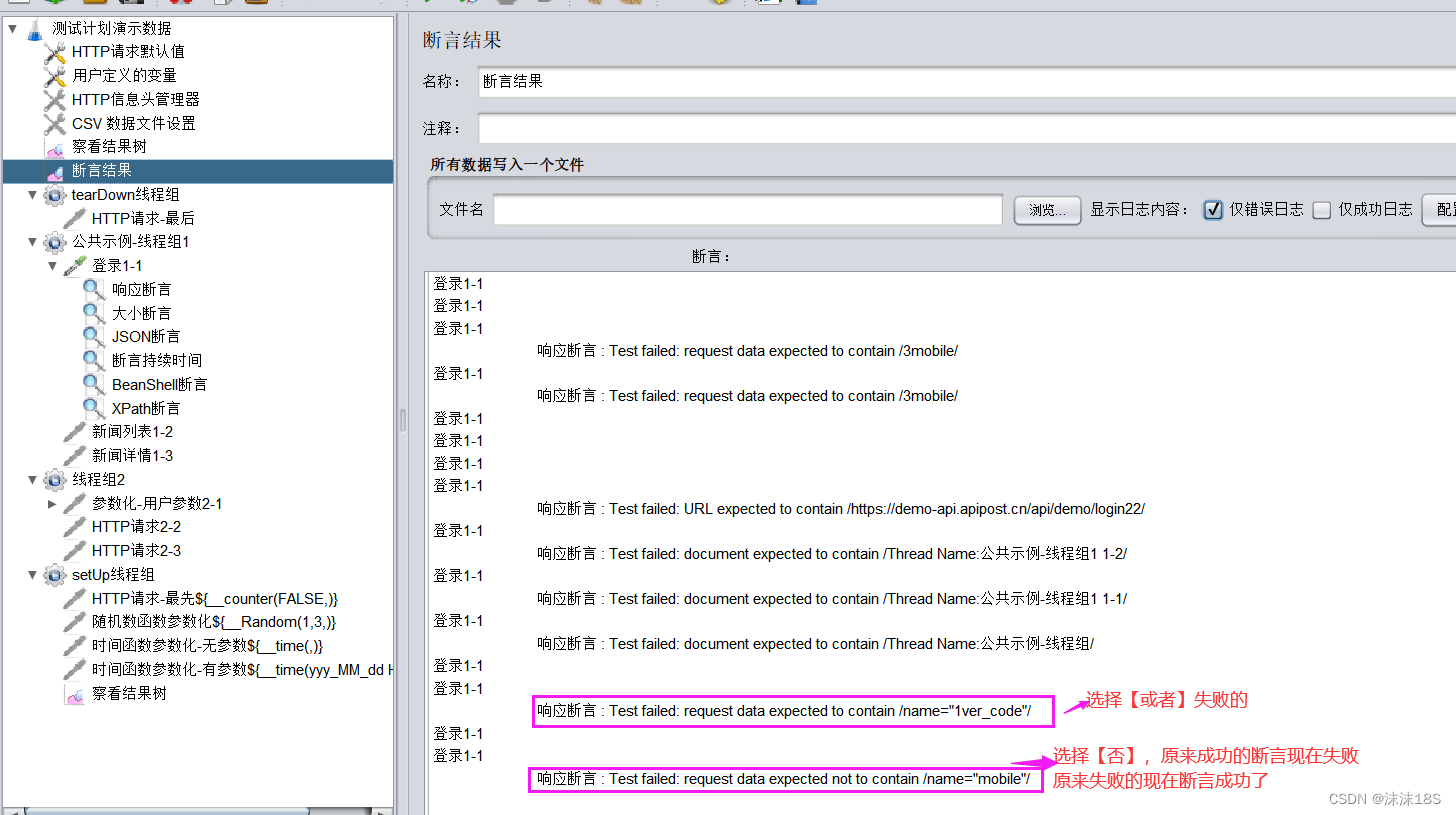
响应断言是最常用的一种断言方法,主要是对响应结果中的文本内容进行断言,比如响应结果是否包含指定的值,或者是否等于指定的值。响应断言可以适用各种返回类型的响应结果,如:Test、html、application/json、applicatio…...
)
【Python学习笔记】36.Python3 MySQL - mysql-connector 驱动(1)
前言 MySQL 是最流行的关系型数据库管理系统,本章节为大家介绍使用 mysql-connector 来连接使用 MySQL, mysql-connector 是 MySQL 官方提供的驱动器。 Python3 MySQL - mysql-connector 驱动 我们可以使用 pip 命令来安装 mysql-connector࿱…...

计算机SCI论文课题设计需要注意什么? - 易智编译EaseEditing
课题设计就要本着严谨性和可行性来进行。实验设计的类型要选择准确,统计学的方法要运用合理,研究对象和观察指标的选择也要符合研究目的的要求,技术路线要清晰明了。 关于课题的设计的可行性也要综合考虑,比如前期的相关工作基础…...
Quartz入门教程
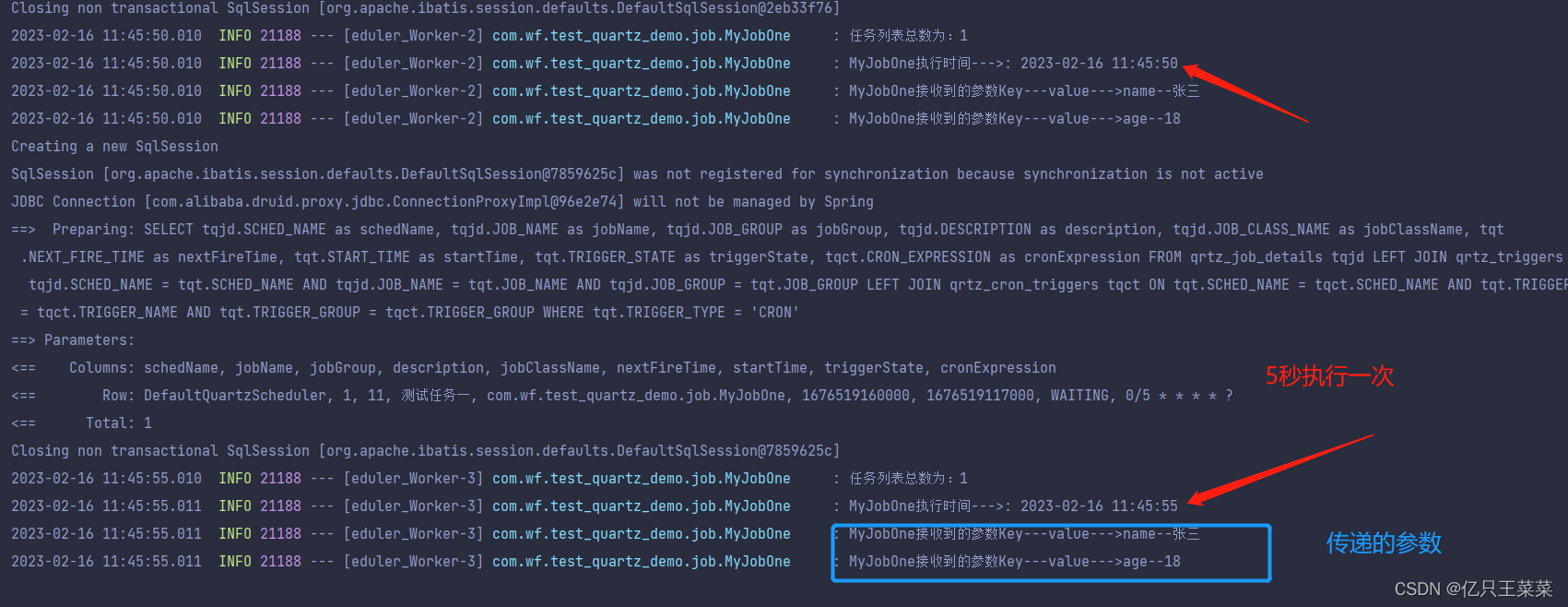
本文参考文章编写 Quartz 官网 Quartz 是 OpenSymphony 开源组织在 Job Scheduling 领域又一个开源项目,是完全由 Java 开发的一个开源任务日程管理系统,“任务进度管理器”就是一个在预先确定(被纳入日程)的时间到达时ÿ…...

TypeScript 学习之 function
函数可以实现抽象层,模拟类,信息隐藏和模块。 函数有:有名字的函数、匿名函数 在 JavaScript 中的函数 // 有名字的函数 function add(x, y) {return x y; }// 匿名函数 let myAdd function (x, y) {return x y; };函数类型 typescript 可…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...
