【2611. 老鼠和奶酪】

来源：力扣（LeetCode）

描述：

有两只老鼠和 n 块不同类型的奶酪，每块奶酪都只能被其中一只老鼠吃掉。

下标为 i 处的奶酪被吃掉的得分为：

• 如果第一只老鼠吃掉，则得分为 reward1[i] 。
• 如果第二只老鼠吃掉，则得分为 reward2[i] 。

给你一个正整数数组 reward1 ，一个正整数数组 reward2 ，和一个非负整数 k 。

请你返回第一只老鼠恰好吃掉 k 块奶酪的情况下，最大 得分为多少。

示例 1：

输入：reward1 = [1,1,3,4], reward2 = [4,4,1,1], k = 2
输出：15
解释：这个例子中，第一只老鼠吃掉第 2 和 3 块奶酪（下标从 0 开始），第二只老鼠吃掉第 0 和 1 块奶酪。
总得分为 4 + 4 + 3 + 4 = 15 。
15 是最高得分。

示例 2：

输入：reward1 = [1,1], reward2 = [1,1], k = 2
输出：2
解释：这个例子中，第一只老鼠吃掉第 0 和 1 块奶酪（下标从 0 开始），第二只老鼠不吃任何奶酪。
总得分为 1 + 1 = 2 。
2 是最高得分。

提示：

• 1 <= n == reward1.length == reward2.length <= 10⁵
• 1 <= reward1[i], reward2[i] <= 1000
• 0 <= k <= n

方法：贪心 + 排序

有 n 块不同类型的奶酪，分别位于下标 0 到 n − 1。下标 i 处的奶酪被第一只老鼠吃掉的得分为 reward₁[i]，被第二只老鼠吃掉的得分为 reward₂[i]。

如果 n 块奶酪都被第二只老鼠吃掉，则得分为数组 reward₂ 的元素之和，记为 sum。如果下标 i 处的奶酪被第一只老鼠吃掉，则得分的变化量是 reward₁[i] − reward₂[i]。

创建长度为 n 的数组 diffs，其中 diffs[i] = reward₁[i]−reward₂[i]。题目要求计算第一只老鼠恰好吃掉 k 块奶酪的情况下的最大得分，假设第一只老鼠吃掉的 k 块奶酪的下标分别是 i₁ 到 i_k，则总得分为：

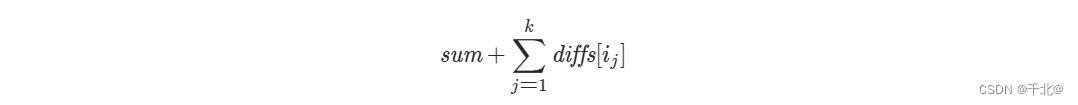
其中 sum 为确定的值。根据贪心思想，为了使总得分最大化，应使下标 i₁ 到 i_k 对应的 diffs 的值最大，即应该选择 diffs 中的 k 个最大值。

贪心思想的正确性说明如下：假设下标 i₁ 到 i_k 对应的 diffs 的值不是最大的 k 个值，则一定存在下标 i_j 和下标 p 满足 diffs[p] ≥ diffs[i_j] 且 p 不在 i₁ 到 i_k 的 k 个下标中，将 diffs[i_j] 替换成 diffs[p] 之后的总得分不变或增加。因此使用贪心思想可以使总得分最大。

具体做法是，将数组 diffs 排序，然后计算 sum 与数组 diffs 的 k 个最大值之和，即为第一只老鼠恰好吃掉 k 块奶酪的情况下的最大得分。

代码：

class Solution {
public:int miceAndCheese(vector<int>& reward1, vector<int>& reward2, int k) {int ans = 0;int n = reward1.size();vector<int> diffs(n);for (int i = 0; i < n; i++) {ans += reward2[i];diffs[i] = reward1[i] - reward2[i];}sort(diffs.begin(), diffs.end());for (int i = 1; i <= k; i++) {ans += diffs[n - i];}return ans;}
};

执行用时：124ms, 在所有 C++ 提交中击败了69.45%的用户
内存消耗：101 MB, 在所有 C++ 提交中击败了82.99%的用户
复杂度分析
时间复杂度：O(nlogn)，其中 n 是数组 reward₁ 和 reward₂ 的长度。创建数组 diffs 需要 O(n) 的时间，将数组 diffs 排序需要 O(nlogn) 的时间，排序后计算 diffs 的 k 个最大值之和需要 O(k) 的时间，其中 k ≤ n，因此时间复杂度是 O(nlogn)。
空间复杂度：O(n)，其中 n 是数组 reward₁ 和 reward₂ 的长度。需要创建长度为 n 的数组 diffs 并排序，数组需要 O(n) 的空间，排序需要 O(logn) 的递归调用栈空间，因此空间复杂度是 O(n)。

方法二：贪心 + 优先队列

方法一当中，计算最大得分的做法是创建长度为 n 的数组 diffs，其中 diffs[i] = reward₁[i] − reward₂[i]，将数组 diffs 排序之后计算 sum 与数组 diffs 的 k 个最大值之和。也可以使用优先队列存储数组 diffs 中的 k 个最大值，优先队列的队首元素为最小元素，优先队列的空间是 O(k)。

用 sum 表示数组 reward₂ 的元素之和。同时遍历数组 reward₁ 和 reward₂，当遍历到下标 i 时，执行如下操作。

将 reward₁[i] − reward₂[i] 添加到优先队列。

如果优先队列中的元素个数大于 k，则取出优先队列的队首元素，确保优先队列中的元素个数不超过 k。

遍历结束时，优先队列中有 k 个元素，为数组 reward₁ 和 reward₂ 的 k 个最大差值。计算 sum 与优先队列中的 k 个元素之和，即为第一只老鼠恰好吃掉 k 块奶酪的情况下的最大得分。

代码：

class Solution {
public:int miceAndCheese(vector<int>& reward1, vector<int>& reward2, int k) {int ans = 0;int n = reward1.size();priority_queue<int, vector<int>, greater<int>> pq;for (int i = 0; i < n; i++) {ans += reward2[i];pq.emplace(reward1[i] - reward2[i]);if (pq.size() > k) {pq.pop();}}while (!pq.empty()) {ans += pq.top();pq.pop();}return ans;}
};

执行用时：152ms, 在所有 C++ 提交中击败了45.26%的用户
内存消耗：102.4 MB, 在所有 C++ 提交中击败了63.91%的用户
复杂度分析
时间复杂度：O(nlogk)，其中 n 是数组 reward₁ 和 reward₂ 的长度，k 是第一只老鼠吃掉的奶酪块数。遍历两个数组的过程中，每个下标处的优先队列操作时间是 O(logk)，共需要 O(nlogk) 的时间，遍历数组之后计算优先队列中的 k 个元素之和需要 O(klogk) 的时间，其中 k ≤ n，因此时间复杂度是 O(nlogk+klogk) = O(nlogk)。
空间复杂度：O(k)，其中 k 是第一只老鼠吃掉的奶酪块数。优先队列需要 O(k) 的空间。
author：LeetCode-Solution