二叉树详解:带你掌握二叉树
目录
- 前言
- 1. 树型结构
- 1. 1 树的概念
- 1.2 树的特点
- 1.3 树的相关术语
- 2. 二叉树(binary tree)
- 2.1 二叉树的概念
- 2.2 二叉树中的特殊树
- 2.2.1 满二叉树
- 2.2.2 完全二叉树
- 2.3 二叉树的性质
- 3. 二叉树的遍历
- 3.1 前序遍历
- 3.2 中序遍历
- 3.3 后序遍历
- 3.4 层序遍历
- 总结
前言
因为二叉树是一种特殊的树,所以想要学习好二叉树,必须了解树型结构,知道树的基本概念。所以正式开始学习之前,在前面为大家引入了树的概念。
1. 树型结构
1. 1 树的概念
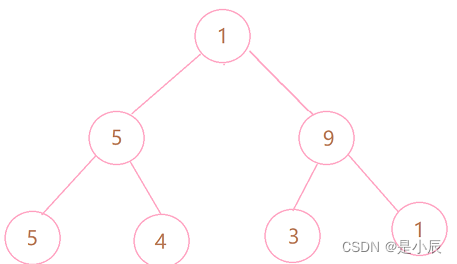
树是一种非线性的数据结构,它是有n个节点构成的集合,把它称为树,是因为这种结构看起来就像一个倒挂的树,根在上面,叶在下面。
1.2 树的特点
- 有一个特殊的节点,没有前驱节点,我们将此称为根节点。
- 树是递归定义的。
- 树的任何节点都可以有任意后继,但是它们不会交叉。
- 树是一个非线性数据结构。
1.3 树的相关术语
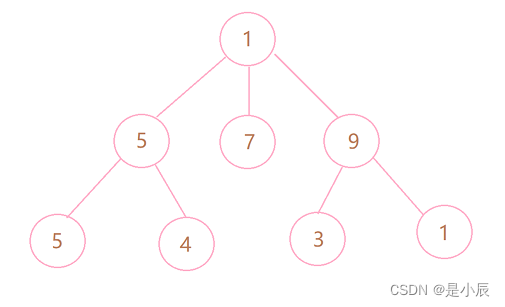
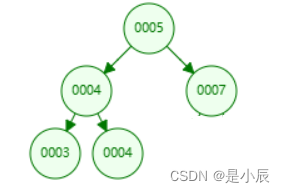
- 根节点:一个特殊节点,没有前驱节点;上图:第一个1 。
- 节点的度:一个节点拥有的子树的多少,就是该节点的度;上图:9的度为:2 。
- 树的度:一棵树最大节点的度就是树的度; 上图:最大的节点的度为3 ,则树的度为3 。
- 叶节点:又称叶子节点,终端节点,度为零的节点;上图:3、4等都是叶节点。
- 父节点:又称双亲节点,父亲节点,一个节点有子节点,则就是这是字节点的父节点;上图:9是3的父节点。
- 子节点:又称孩子节点,一个节点下面与连接的节点就是子节点;上图:3是9的子节点。
- 节点的层次:根节点为第一层,根节点的子节点为第二层,以此类推。
- 树的高度或深度:树中最大的节点的层次。
2. 二叉树(binary tree)
2.1 二叉树的概念
二叉树是一种树形数据结构,是一种特殊的树,二叉树中每个节点最多只能有两个子节点,并且二叉树的次序是不可颠倒的,是一颗有序树。
2.2 二叉树中的特殊树
二叉树是一种特殊的树,而特殊树中还会有特殊。
2.2.1 满二叉树
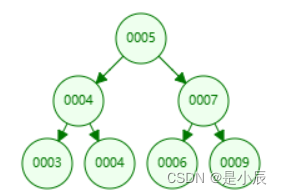
一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵
二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
2.2.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n
个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
- 二叉树是由节点和边构成的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点,没有子节点的节点称为叶子节点。
- 二叉树有一个根节点,其它节点都是根节点的子节点。根节点没有父节点。
- 对于一个有n个节点的二叉树,设其高度为h,则h的取值范围为1到n,且h为log2(n+1)向上取整。
- 在二叉树的第i层上,最多有2^(i-1)个节点。
- 若深度为h的二叉树满足:每个节点都有两个子节点,且所有叶子节点都在第h层或h-1层,则称该树为满二叉树。满二叉树的节点数为2^h-1。
- 若深度为h的二叉树最后一层只有叶子节点,其它层都是满的,则称该树为完全二叉树。完全二叉树的节点数在1到2^(h-1)之间。
- 若二叉树的左右子树可以交换位置且仍为同一棵树,则该二叉树为镜像二叉树。1. 二叉树是由节点和边构成的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点,没有子节点的节点称为叶子节点。
《一些练习的题》
1.某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
3.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
答案:
1.B
2.A
3.B
4.B
3. 二叉树的遍历
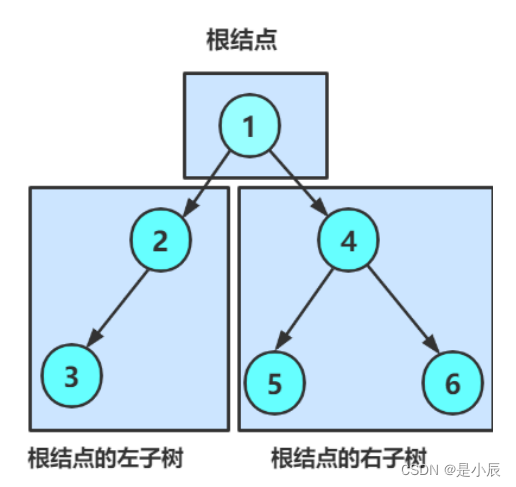
二叉树的遍历是一个重要的点,是一个必须要掌握的点,遍历分为前中后序遍历,层序遍历四种。我们将使用这张图详细介绍一下。
遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
3.1 前序遍历
前序遍历的遍历顺序:访问根结点—>根的左子树—>根的右子树。
遍历结果:123456
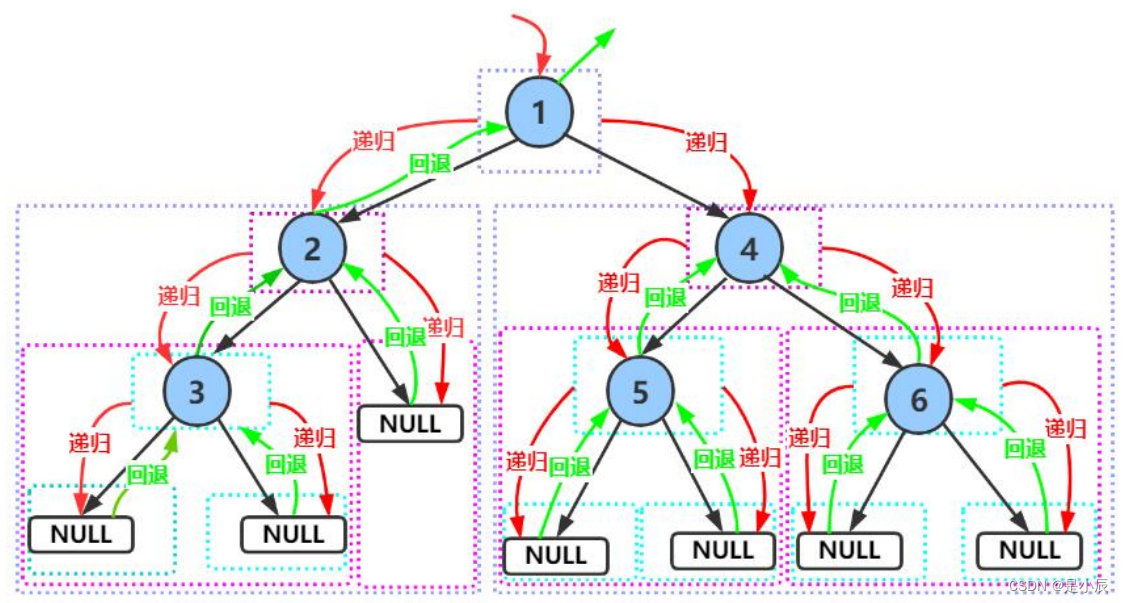
如上图:遍历根节点1,然后遍历左子树2,一直遍历到左子树为null。然后返回途中遍历右子树,3的右子树为null。然后返回到2,2的右子树为null,返回到根节点1。1的左树已经遍历一遍,所以继续遍历1的右子树4,然后先遍历左子树5,5的左右都为空,则返回遍历4的右子树6。6的左右都为空,原路返回,到根节点遍历结束。
3.2 中序遍历
根的左子树—>根节点—>根的右子树。
遍历结果:321546
3.3 后序遍历
根的左子树—>根的右子树—>根节点。
遍历结果:325641
3.4 层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在
层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
遍历结果:124356
一些练习选择题
- 某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA- 二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A: E B: F C: G D: H- 设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde- 某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
【参考答案】 1. A 2. A 3. D 4. A
总结
这篇博客主要为大家带来树及二叉树的基本概念,性质,遍历方式等,下篇博客将为大家带来代码的实现以及应用。
期待大家关注!
最后,祝大家61快乐,天天开心!
相关文章:

二叉树详解:带你掌握二叉树
目录 前言1. 树型结构1. 1 树的概念1.2 树的特点1.3 树的相关术语 2. 二叉树(binary tree)2.1 二叉树的概念2.2 二叉树中的特殊树2.2.1 满二叉树2.2.2 完全二叉树 2.3 二叉树的性质 3. 二叉树的遍历3.1 前序遍历3.2 中序遍历3.3 后序遍历3.4 层序遍历 总…...
LNMP网站框架搭建(编译安装)
目录 一、Nginx的工作原理 工作进程: 二、Nginx编译安装安装 三、mysql的编译安装 四、php的编译安装 验证PHP与nginx的是否连接 验证lnmp的是否搭建成功 五、部署 Discuz!社区论坛 一、Nginx的工作原理 php-fpm.conf 是控制php-fpm守护…...
详解Servlet API
目录 前言 HttpServlet HttpServletRequest 代码实例 打印请求信息 通过URL中的queryString进行传递。 通过post请求的body,使用form表单传递 通过POST 请求中的 body 按照 JSON 的格式进行传递 HttpServletResponse 核心方法代码实例 设置状态码 自动刷…...
【小白教程】Docker安装使用教程,以及常用命令!
【小白教程】Docker安装使用教程,以及常用命令! - 带你薅羊毛最近调试Docker内容,顺手记录一下,我常用的几个命令!这里总结一下,方便自己也同时方便大家使用! 内容慢慢完善更新!如有…...

TypeScript基础
TS编译运行 ts不是在终端运行,是一门中间语言,最终编译为js运行。 手动编译 // 1. ts编译为js npm i -g typescript // 查看版本 tsc -v// 2. ts直接运行,主要用来查看是否报错 npm i -g ts-node // 查看版本 ts-node -v1.手动编译ts代码 …...
QML学习二:Doxygen为qml工程生成代码文档
效果如下: 设置后能够支持.js和.qml文档。 QML学习二:Doxygen为工程生成注释文档 前言一、安装doxyqml二、Doxygen设置1.文档目录设置2.文档目录设置三、添加注释总结前言 好的代码必须配一个好的文档说明,方便以后维护以及学习。 前提条件: 1.安装好了Doxygen代码生成工…...

Vue 有哪些经典面试题?
前言 下面总结了vue的一些经典的面试题,希望对正在找工作面试的小伙伴们提供一些帮助,我们废话少说直接进入整体、 简述一下什么是MVVM模型 MVVM,是Model-View-ViewModel的简写,其本质是MVC模型的升级版。其中 Model 代表数据模…...
pandas速学-DataFrame
一、理解DataFrame 他是一个表格结构:DataFrame 是一个表格型的数据结构 他是有序的,不同值类型:它含有一组有序的列,每列可以是不同的值类型(数值、字符串、布尔型值)。 他可以被看做一个由series组成的…...

在任务与执行策略之间的隐性耦合
我们已经知道, Executor 框架可以将任务的提交与任务的执行策略解耦开来。就像许多对复杂过程的解耦操作那样,这种论断多少有些言过其实了。虽然Executor 框架为制定和修改执行策略都提供了相当大的灵活性,但并非所有的任务都能适用所有的执行…...

Spring Cloud Alibaba Nacos 构建配置中心
构建配置中心 新建命名空间 登录 Nacos 面板,依次点击左侧菜单栏【命名空间→新建命名空间】、填写命名空间名和描述信息,点击【确定】: 新建配置文件 依次点击左侧菜单栏【配置管理→配置列表】、切换到指定命名空间【此处为 shop】、点击…...

华为OD机试真题 Java 实现【猴子爬山】【2023 B卷 100分】,附详细解题思路
一、题目描述 一天一只顽猴想去从山脚爬到山顶,途中经过一个有个N个台阶的阶梯,但是这猴子有一个习惯: 每一次只能跳1步或跳3步,试问猴子通过这个阶梯有多少种不同的跳跃方式? 二、输入描述 输入只有一个整数N(0<N<=50)此阶梯有多少个阶梯。 三、输出描述 输…...

【19JavaScript for 循环】JavaScript for 循环:掌握重复执行的关键
JavaScript for 循环 在JavaScript中,for循环是一种常用的循环结构,它允许您重复执行一段代码,达到循环的目的。 基本语法 for (initialization; condition; iteration) {// 要执行的代码}for循环由以下几个关键部分组成: init…...
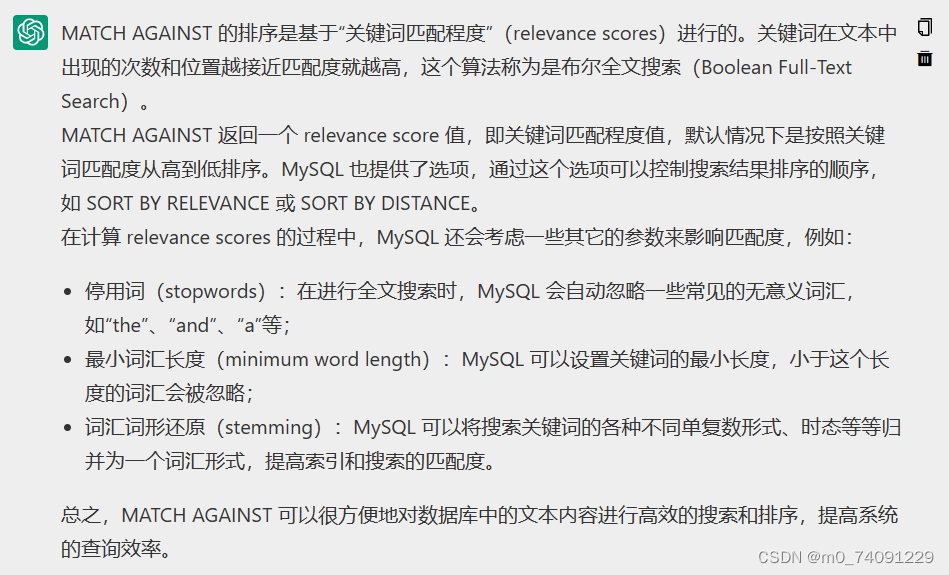
MySQL学习(联结,组合查询,全文本搜索)
联结 SQL最强大的功能之一就是能在数据检索查询的执行中联结表; 关系表 为什么要使用关系表? 使用关系表可以储存数据不重复,从而不浪费时间和空间;如果有数据信息变动,只需更新一个表中的单个记录,相关…...

Nautilus Chain:独特且纯粹的创新型 Layer3
以 Layer3 架构为主要特点的模块化公链 Nautilus Chain 即将在近期上线主网,这也进一步引发了行业关于 Layer3 的讨论。 实际上,在2022年以太坊的创始人 Vitalik 提出了三大目标:Layer2 用于扩展,Layer3 用于定制功能,…...

十六、立方体贴图(天空盒)
第一部分 概念: 1) 引用 OpenGL ES 立方体贴图本质上还是纹理映射,是一种 3D 纹理映射。立方体贴图所使的纹理称为立方图纹理,它是由 6 个单独的 2D 纹理组成,每个 2D 纹理是立方图的一个面。 立方图纹理的采样通过一个 3D 向量…...

UniAD:实现多类别异常检测的统一模型
来源:投稿 作者:Mr.Eraser 编辑:学姐 论文标题:用于多类异常检测的统一模型 论文链接:https://arxiv.org/abs/2206.03687 论文贡献: 提出UniAD,它以一个统一框架完成了多个类别的异常检测。 …...
)
Java 面试 | tcp ip http https(2023版)
文章目录 HTTP&HTTPS1、Http和Https的区别?2、什么是对称加密与非对称加密3、客户端不断进行请求链接会怎样?DDos(Distributed Denial of Service)攻击?4、GET 与 POST 的区别?5、什么是 HTTP 协议无状态协议?怎么解决Http协议无状态协议?6、Session、Cookie 与 Appl…...
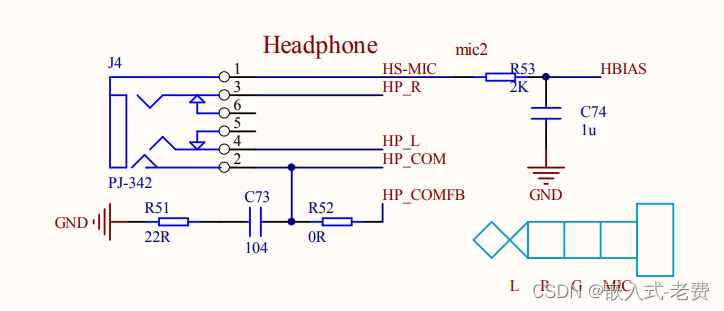
全志V3S嵌入式驱动开发(音频输出和音频录制)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 之前在芯片公司的时候,基本没有看过音频这一块,只知道有个alsa框架这么个知识点。要驱动音频,需要两部分&#…...

使用RP2040自制的树莓派pico—— [2/100] HelloWorld! 和 点亮LED
使用RP2040自制的树莓派pico—— [2/100] HelloWorld! 和 点亮LED 开发环境HelloWorld!闪烁 LED 灯代码 由于比较简单就放在一起写了 开发环境 软件:Thonny HelloWorld! 要想使串口打印HelloWorld! 只需要一行代码 print("HelloWorld!")保…...
康耐视In-Sight2800相机的使用
In-Sight2800相机注册分类程序 一、登录相机 二、图像导入 IS相机支持拍摄图像和从文件中导入图像 如选择从文件中导入图像,文件夹选择位置在页面左下方,如下图 三、注册分类器 在检查模块注册分类器,注册图像需要一张一张去学习&#x…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...