11.无监督学习之主成分分析
11.1 降维
降维的两种应用:一是数据压缩;二是可视化数据。
11.1.1 数据压缩
将相关性强的两个特征导致冗余,可以直接去掉其中一个特征,或者将两个特征进行某种转换,得到一个特征。

11.1.2 可视化数据
直接看数据可能看不出什么现象出来

但是通过图来进行对比,按照GDP或者是其他标准来看,会更明显。

11.2 主成分分析(PCA)
假设我们有一个二维的样本x数据集,当我们向对数据进行降维从二维到一维,也就是想到找一条能够将数据投影成一条直线。PCA会找一个低维得平面,刚刚的假设例子是一条直线,然后将数据投影在上面使这些蓝色小线段长度(有时也叫投影误差)平方最小,PCA要做的就是找到一个投影平面对数据进行投影使得能最小化这个距离。

主成分分析(PCA)是一种数据压缩的算法,他将数据压缩到k维度,并使得所有数据投影到新维度的距离最小。在应用PCA之前,常规的做法是先进行均值归一化和特征常规化,使得特征得均值为0并且其数值在可比较范围之内。

PCA做的就是,对于二维降到一维:要试着找到一个向量,假设是(
),要找一个数据投影后能够最小化投影误差的方向,在这个例子里,希望PCA能找到这个向量
。当把数据投影到
存在的这条直线上时,就会得到非常小的重构误差(如上图所示)。
对于N维降到K维:我们要找的就不是单个向量来对数据进行投影二是想寻找K个方向来对数据进行投影来最小化投影误差。
PCA不是线性回归,一个是投影距离,一个是点与直线上点的距离。
下图的左边部分表示线性回归,当我们处理线性回归时,给定某个输入的特征量x来预测出某变量y的值。所以在线性回归中,我们要做的就是拟合一条直线来最小化点和直线之间的平方误差,要最小化的是图中蓝线之和的平方。下图的右边部分表示PCA,在处理PCA中,它要做的是试图最小化这些蓝色直线的长度(是他们最短的正交距离)。线性回归垂直x轴,求预测与实际y差;而PCA是垂直于拟合线,求正交距离。

并且线性回归是用所有的x来预测y,在PCA中没有区别对待,没有什么特殊的变量y需要预测,相反我们有一系列特征都是同等对待。
PCA执行过程:首先对数据预处理,进行均值归一化(可能也要进行特征缩放),然后计算协方差,最后得到一个k维的矩阵。

首先对数据进行均值归一化,然后确定要压缩的目标维度,即对应向量的个数,PCA的目标是使得所有数据距离新维度的距离最小。

将n维降到k维,下面是过程:
在进行数据预处理后,首先计算协方差(covariance matrix)Sigma是nxn的矩阵, 再进行特征缩放。



11.3 压缩重现
怎么样把降维的数据再重现回去?

(这里反求的x是近似的)
11.4 确定维度K
为了选择k也就是主要成分的数量,这里有一些有用的概念。
PCA所做的是尝试使得这个式子最小化,这就是平均平方差投影误差。训练集数据的总方差:
(所有训练实例的范数得平均值)。也就是说,它代表了我的数据点与(0,0)点平均有多远。当我们选择k时,我们要取得最小值的k,使得下图的不等式小于等于0.01。

选择k使得平均投影平方误差(分子)除以总方差(分母),也就是代表数据波动有多大。这里的0.01,用术语说就是保留99%的方差特性,也就是降维后保留的数据量要占到原数据的99%以上。variance在这里不应该理解成为方差而是差异,PCA其实是保留差异的分量,将具有相关性。可能95%到99%是最常使用的数值。因为很多数据特征相关,所以降维依然可以保留95%以上的特征。
实现这一点的步骤如下:
如果你想要k的值,让k=1,执行PCA算法,计算下面这些变量的值,然后检查下面不等式是否满足小于等于0.01,如果不成立继续让k=2,k=3,k=4...;如果成立就选择k=1。但是这样做效率不高。

可以使用PCA运算中已经写好的svd分解函数,调用svd,通过Sigma参数,得到U,S,V三个参数。其中,S矩阵是一个对角阵。并且可以证明对于给定的k,将变换成
这样计算,接下来要做的就是验证它是否小于等于0.01,或者验证
是否大于0.99。


11.5 PCA的应用

如果直接再交叉验证集和测试集上用PCA会过拟合,所以只能用训练集降维矩阵去给测试机和交叉验证集做映射,不能另外在上面做PCA。
PCA的应用:首先它能进行数据压缩,其次可以使用PCA去加速学习算法以及可视化。
PCA不能防止过拟合!过拟合是由于某些异常数据的影响而产生的,通过主成分分析只能去除异常数据内部的一部分噪音,并不能把异常数据本身从数据集中去除,异常数据在投影面上的异常性还是存在。解决过拟合的好方式使用正则化。
PCA有时候会丢失一些重要的数据信息,这样训练出来的模型性能会减弱,除非数据太大或者算法太慢才会考虑PCA。

相关文章:

11.无监督学习之主成分分析
11.1 降维 降维的两种应用:一是数据压缩;二是可视化数据。 11.1.1 数据压缩 将相关性强的两个特征导致冗余,可以直接去掉其中一个特征,或者将两个特征进行某种转换,得到一个特征。 11.1.2 可视化数据 直接看数据可…...

「HTML和CSS入门指南」figcaption 标签详解
什么是 figcaption 标签? 在 HTML 中,figcaption 标签用于为与 figure 元素相关的媒体内容提供说明性文本。通常用于包含图像、音频或视频等媒体元素的说明文本。 figcaption 标签的基本语法 以下是 figcaption 标签的基本语法: <figure><!-- 在这里放置您的媒体…...

电子企业实施数字化工厂建设之前,需要注意哪些
随着工业4.0时代的到来,数字化工厂建设已成为越来越多电子企业的重要议题。数字化工厂管理系统能够提高生产效率、降低成本、提高产品质量等多个方面的优势,对于企业的可持续发展具有重要意义。然而,在实施电子企业数字化工厂建设之前&#x…...
迅捷pdf实现多页插入
之前我们使用福昕阅读器实现了在每一页插入logo 这里我们用迅捷pdf再来一次,别问,问就是公司买了会员 首先声明,这里已经有会员了,所以不知道别人操作是不是需要会员,担心的话可以看看上一篇福昕阅读器版本 打开编辑…...

调用阿里云API实现证件照生成
目录 1. 作者介绍2. 算法介绍2.1 阿里云介绍2.2 证件照生成背景2.3 图像分割算法 3.调用阿里云API进行证件照生成实例3.1 准备工作3.2 实验代码3.3 实验结果与分析 参考(可供参考的链接和引用文献) 1. 作者介绍 王逸腾,男,西安工…...

PHP 转换 excel中读取的时间
首先,我们需要知道PHPExcel的时间和日期格式是以Excel内部的“1900年1月1日”为基础,以天为单位来计算的。即Excel日期与PHP时间戳之间存在一个时间偏移量。通过查阅PHPExcel的官方文档,我们可以得到以下的计算公式: // 读取exce…...
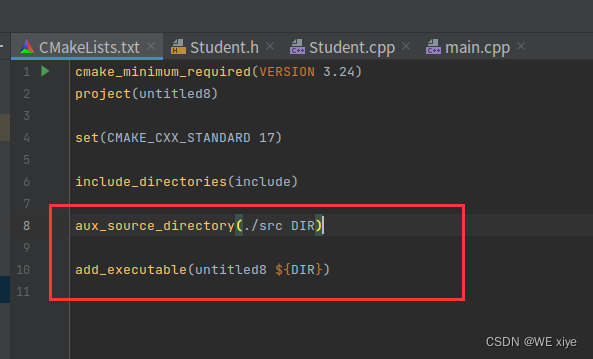
Cmake工具的简单使用
引言 本篇文章讲述如何简单的使用cmake工具构建一个项目,帮助入门的c新手学会如何使用cmake. 我们在Clion新创建一个项目时,会发现,除了main.cpp文件之外,还存在一个build-debug目录和一个CMakelists.txt文件,如图: …...

html选择器
基本选择器 基本选择器 : 标签选择器 , 类选择器 , ID选择器 标签选择器 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEed…...

Leetcode 剑指 Offer II 030. 插入、删除和随机访问都是 O(1) 的容器
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 设计一个支持在平均 时间复杂度 O(1) 下,执行以下操作…...

django实现读取数据导出生成excel表格
目录 一、简单示例: 1.创建文件对象: 2.添加工作表: 3.写入数据: 二、实践出真理 需要先安装xlwt模块 pip install -i https://pypi.douban.com/simple xlwt一、简单示例: import xlwt# 创建一个Excel文件对象 …...

DevOps系列文章之 Docker-compose
一,Docker-compose全集 1,Docker-compose简介 Docker-Compose项目是Docker官方的开源项目,负责实现对Docker容器集群的快速编排。 Docker-Compose将所管理的容器分为三层,分别是工程(project),…...

Vue Router入门:轻松构建单页应用程序
Vue.js是一种流行的前端JavaScript框架,可以让开发人员轻松构建动态用户界面。Vue.js的一个关键特性是其路由系统,它使得开发人员可以轻松创建具有多个视图和页面的单页应用程序(SPA)。在本文中,我们将探讨如何使用Vue Router在Vue.js中构建SPA。我们将介绍如何安装和配置…...

ITSM 如何帮助制造业企业
ITSM在现代制造业中的作用 在过去的几年中,制造业已经看到了快速的数字化,以智能制造技术改进生产技术。在工业4.0和工业5.0的推动下,制造商正在摆脱陈旧 以及利用物联网、人工智能、机器学习和大数据等先进技术的互联智能制造系统ÿ…...

leecode
leecode20,有效的括号,栈 class Solution:def isValid(self, s: str) -> bool:def check(ch1,ch2):if ch1 [ and ch2 ]:return Trueelif ch1 ( and ch2 ):return Trueelif ch1 { and ch2 }:return Trueelse:return Falsestack []for i in ran…...
<未来补全>)
2023-06-09 LeetCode每日一题(修改图中的边权)<未来补全>
2023-06-09每日一题 一、题目编号 2699. 修改图中的边权二、题目链接 点击跳转到题目位置 三、题目描述 给你一个 n 个节点的 无向带权连通 图,节点编号为 0 到 n - 1 ,再给你一个整数数组 edges ,其中 edges[i] [ai, bi, wi] 表示节点…...

Linux 应用程序信号量使用实战
背景 在项目实施过程中,有个机制需要做两个线程之间的同步。 具体需求如下: 首先,线程1需要把资源读取到缓存 其次,线程2才可以操作这块缓存 上述两个动作顺序交替重复。 思路 使用信号量解决思路,申请两个信号…...

【Java多线程进阶】synchronized工作原理
前言 本期讲解 synchronized 工作的原理以及常见的锁优化机制,相信大家在看完这篇博文后对 synchronized 工作流程有一定的理解。话不多说,让我们快速进入学习吧~ 目录 1. 锁的工作流程 2. 偏向锁 3. 轻量级锁和重量级锁 3.1 轻量级锁 3.2 重量级锁…...
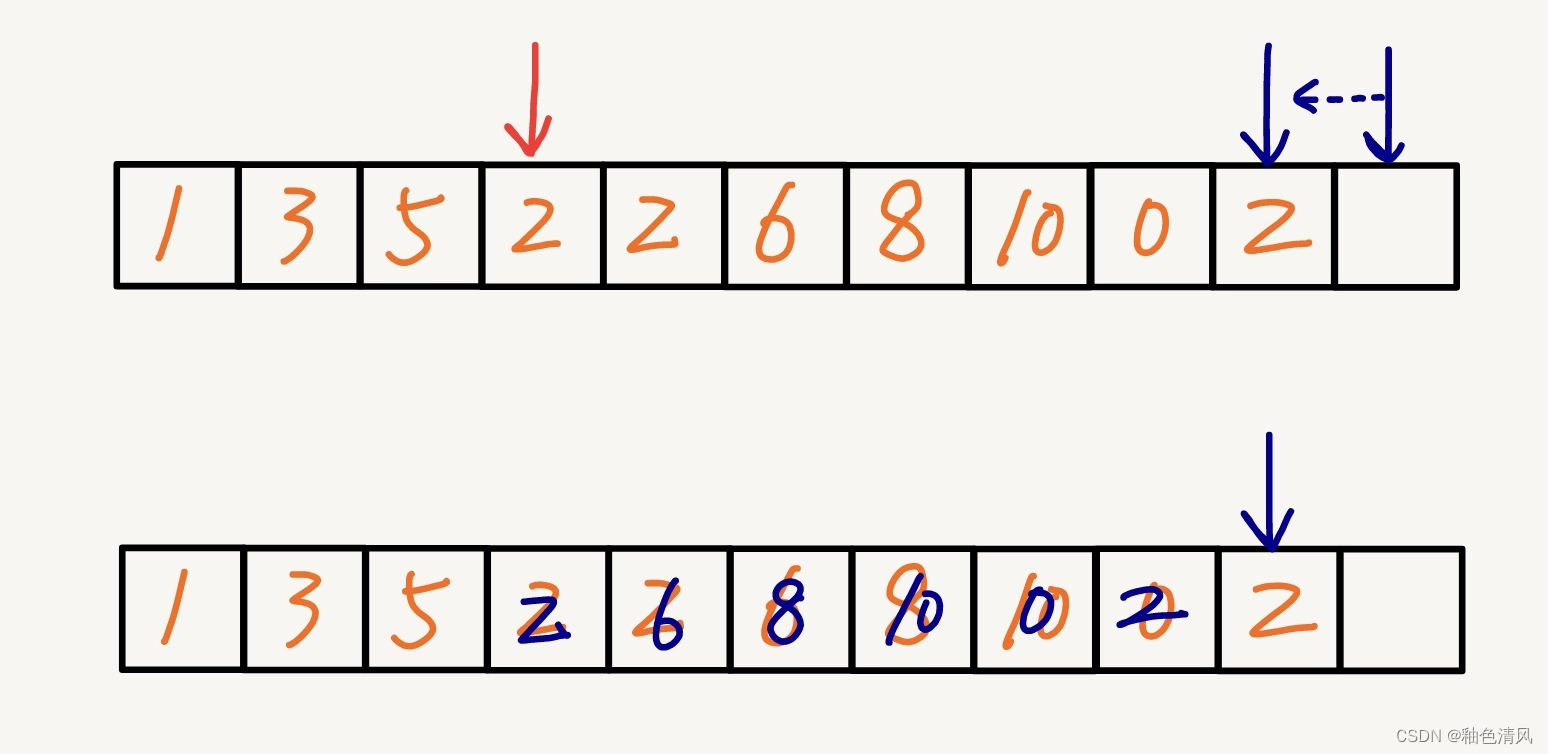
C语言经典题目(三)
C站的小伙伴们,大家好呀!😊😊✨✨这一篇是C语言之经典题目篇,除程序设计,还有一些不错的程序分析,快来和我一起进入C语言的世界吧!✨✨✨ 💕C语言其他刷题篇在这里哦&…...
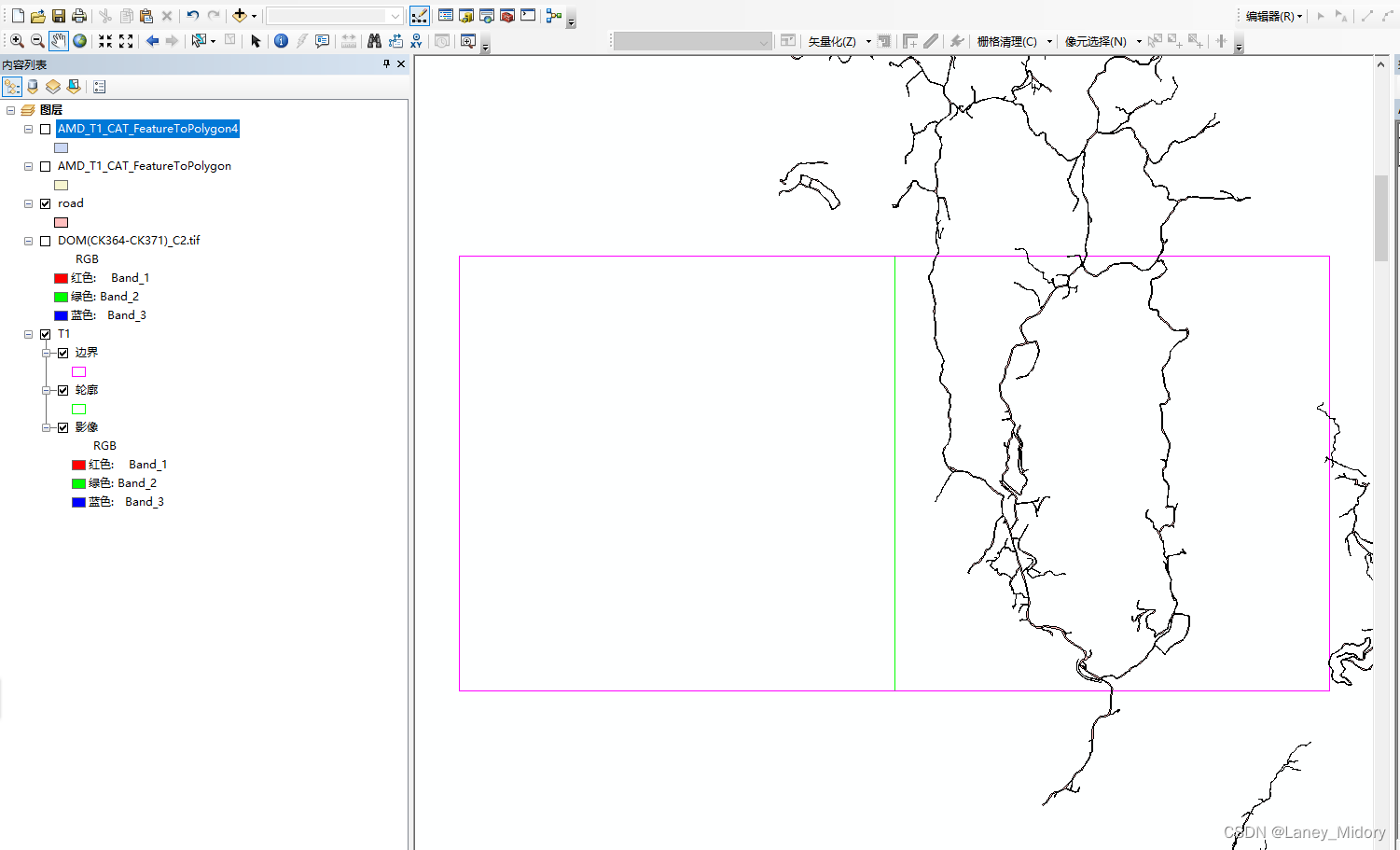
九、(补充文章四)Arcgis实现深度学习训练样本数据的批量制作——只靠原图+shp如何批量制作样本图片
之前写了一些个深度学习系列文 其中先是单张样本的制作方法 最后通过构造模型批量处理 大大提高了生成样本的速度 四、Arcgis实现深度学习河流训练样本数据的制作(使用软件批量获取样本图片)——对已经获取到的完整面状样本数据进行处理 但是这个方法不仅仅需要shp和原图 还需要…...
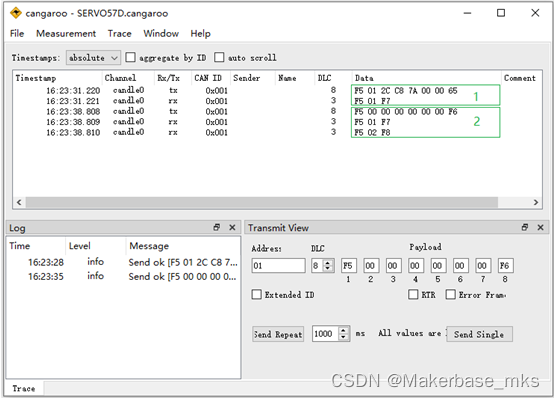
MKS SERVO4257D 闭环步进电机_系列8 CAN通讯示例
第1部分 产品介绍 MKS SERVO 28D/35D/42D/57D 系列闭环步进电机是创客基地为满足市场需求而自主研发的一款产品。具备脉冲接口和RS485/CAN串行接口,支持MODBUS-RTU通讯协议,内置高效FOC矢量算法,采用高精度编码器,通过位置反馈&a…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
