代码随想录第55天
1.判断子序列:
动态规划五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
注意这里是判断s是否为t的子序列。即t的长度是大于等于s的。
如果t的长度小于s那直接return false,如果s的长度为0,是return true;
有同学问了,为啥要表示下标i-1为结尾的字符串呢,为啥不表示下标i为结尾的字符串呢?
为什么这么定义我在 718. 最长重复子数组 (opens new window)中做了详细的讲解。
其实用i来表示也可以!
但我统一以下标i-1为结尾的字符串来计算,这样在下面的递归公式中会容易理解一些,如果还有疑惑,可以继续往下看。
2.确定递推公式
在确定递推公式的时候,首先要考虑如下两种操作,整理如下:
- if (s[i - 1] == t[j - 1])
- t中找到了一个字符在s中也出现了
- if (s[i - 1] != t[j - 1])
- 相当于t要删除元素,继续匹配
if (s[i - 1] == t[j - 1]),那么dp[i][j] = dp[i - 1][j - 1] + 1;,因为找到了一个相同的字符,相同子序列长度自然要在dp[i-1][j-1]的基础上加1(如果不理解,在回看一下dp[i][j]的定义)
if (s[i - 1] != t[j - 1]),此时相当于t要删除元素,t如果把当前元素t[j - 1]删除,那么dp[i][j] 的数值就是 看s[i - 1]与 t[j - 2]的比较结果了,即:dp[i][j] = dp[i][j - 1];
其实这里 大家可以发现和 1143.最长公共子序列 (opens new window)的递推公式基本那就是一样的,区别就是 本题 如果删元素一定是字符串t,而 1143.最长公共子序列 是两个字符串都可以删元素。
3.dp数组如何初始化
从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],所以dp[0][0]和dp[i][0]是一定要初始化的。
这里大家已经可以发现,在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。
因为这样的定义在dp二维矩阵中可以留出初始化的区间,如图:

如果要是定义的dp[i][j]是以下标i为结尾的字符串s和以下标j为结尾的字符串t,初始化就比较麻烦了。
dp[i][0] 表示以下标i-1为结尾的字符串,与空字符串的相同子序列长度,所以为0. dp[0][j]同理。
vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
4.确定遍历顺序
同理从递推公式可以看出dp[i][j]都是依赖于dp[i - 1][j - 1] 和 dp[i][j - 1],那么遍历顺序也应该是从上到下,从左到右
如图所示:
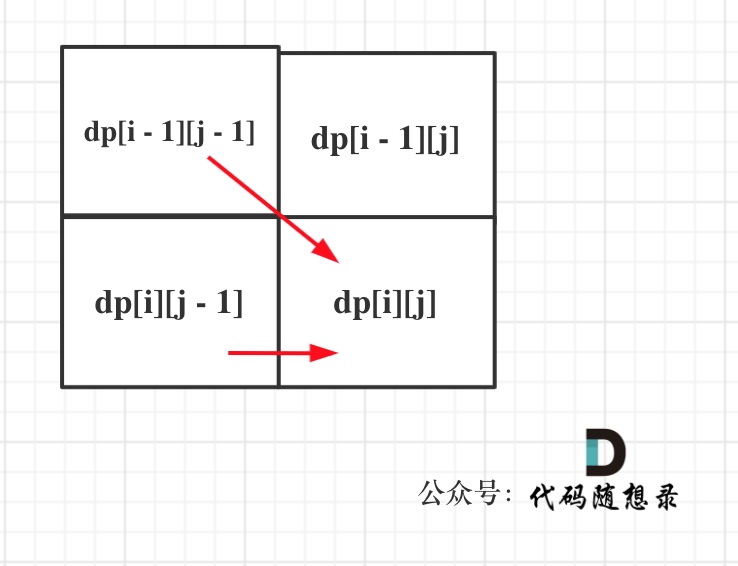
5.举例推导dp数组
以示例一为例,输入:s = "abc", t = "ahbgdc",dp状态转移图如下:
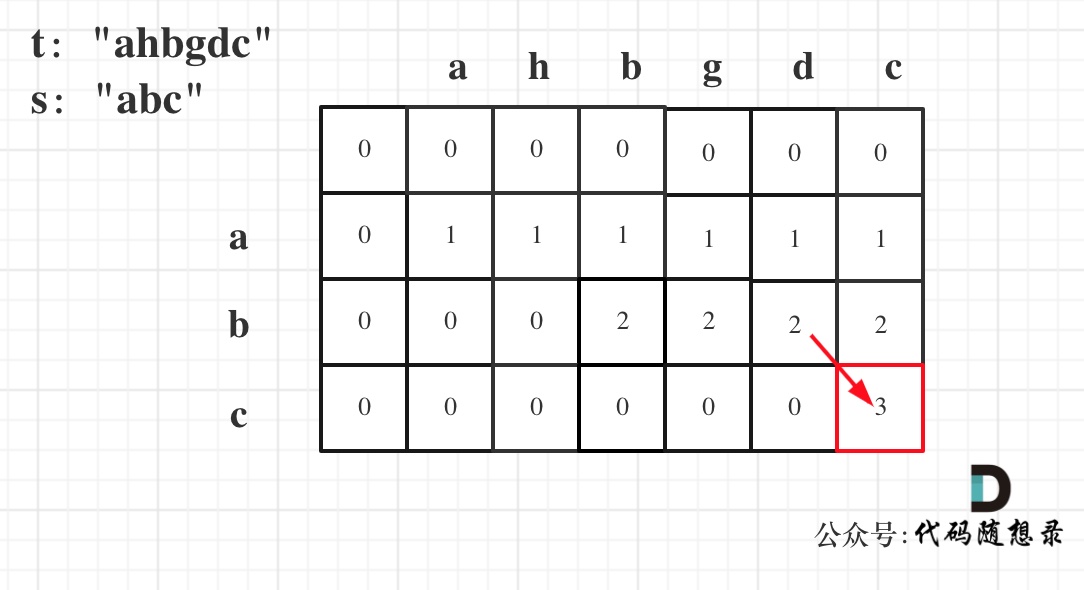
dp[i][j]表示以下标i-1为结尾的字符串s和以下标j-1为结尾的字符串t 相同子序列的长度,所以如果dp[s.size()][t.size()] 与 字符串s的长度相同说明:s与t的最长相同子序列就是s,那么s 就是 t 的子序列。
图中dp[s.size()][t.size()] = 3, 而s.size() 也为3。所以s是t 的子序列,返回true。
动规五部曲分析完毕,C++代码如下:
class Solution {
public:bool isSubsequence(string s, string t) {vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = dp[i][j - 1];}}if (dp[s.size()][t.size()] == s.size()) return true;return false;}
};
2.不同的子序列:
这道题目如果不是子序列,而是要求连续序列的,那就可以考虑用KMP。
这道题的问题就是s里边删除元素变成t的方法数
动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
为什么i-1,j-1 这么定义我在 718. 最长重复子数组 (opens new window)中做了详细的讲解。
2.确定递推公式
这一类问题,基本是要分析两种情况
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。
在判断子序列中这里是加1的,那这道题为什么不加1?
因为判断子序列中求的是s和t的相同子序列的长度;而这道题求的是s里边删除元素变成t的方法数,所以当s[i - 1] 与 t[j - 1]相等时,方法数不变
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
这里可能有录友不明白了,为什么还要考虑 不用s[i - 1]来匹配,都相同了指定要匹配啊。
例如: s:bagg 和 t:bag ,s[3] 和 t[2]是相同的,但是字符串s也可以不用s[3]来匹配,即用s[0]s[1]s[2]组成的bag。
当然也可以用s[3]来匹配,即:s[0]s[1]s[3]组成的bag。
所以当s[i - 1] 与 t[j - 1]相等时,dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
首先他是方法数,然后dp[i][j]是以s[i-1]为结尾的s的子序列中找以j-1为结尾的t(dp数组的含义),其实他是由dp[i-1][j]为基础推出来的,只不过是当s[i - 1] 与 t[j - 1]相等时多了一个情况,就是以s[i-1]为结尾去代替dp[i-1][j]种方法中的结尾字母,最后是把他们加起来,相当于dp[i - 1][j - 1]是增量。
这个不相等时就相当于没有增量。
当s[i - 1] 与 t[j - 1]不相等时,dp[i][j]只有一部分组成,不用s[i - 1]来匹配(就是模拟在s中删除这个元素),即:dp[i - 1][j]
所以递推公式为:dp[i][j] = dp[i - 1][j];
这里可能有录友还疑惑,为什么只考虑 “不用s[i - 1]来匹配” 这种情况, 不考虑 “不用t[j - 1]来匹配” 的情况呢。
这里大家要明确,我们求的是 s 中有多少个 t,而不是 求t中有多少个s,所以只考虑 s中删除元素的情况,即 不用s[i - 1]来匹配 的情况。
3.dp数组如何初始化
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来,如图:,那么 dp[i][0] 和dp[0][j]是一定要初始化的。

每次当初始化的时候,都要回顾一下dp[i][j]的定义,不要凭感觉初始化。
dp[i][0]表示什么呢?
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数(也就是方法数)就是1。
再来看dp[0][j],dp[0][j]:空字符串s可以随便删除元素,出现以j-1为结尾的字符串t的个数。
那么dp[0][j]一定都是0,s如论如何也变成不了t。
最后就要看一个特殊位置了,即:dp[0][0] 应该是多少。
dp[0][0]应该是1,空字符串s,可以删除0个元素,变成空字符串t。
初始化分析完毕,代码如下:
vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0; // 其实这行代码可以和dp数组初始化的时候放在一起,但我为了凸显初始化的逻辑,所以还是加上了。
4.确定遍历顺序
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。

所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
代码如下:
for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}
}
5.举例推导dp数组
以s:"baegg",t:"bag"为例,推导dp数组状态如下:

动规五部曲分析完毕,代码如下:
class Solution {
public:int numDistinct(string s, string t) {vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));for (int i = 0; i < s.size(); i++) dp[i][0] = 1;for (int j = 1; j < t.size(); j++) dp[0][j] = 0;for (int i = 1; i <= s.size(); i++) {for (int j = 1; j <= t.size(); j++) {if (s[i - 1] == t[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];} else {dp[i][j] = dp[i - 1][j];}}}return dp[s.size()][t.size()];}
};32 位的有符号整数的取值范围以及数值溢出
【C语言】uint8_t、uint16_t、uint32_t、uint64_t是什么?
int的取值范围为:-2^31 ---- 2^31-1 ,即:-2147483648 - 2147483647
uint32_t.min=0 uint32_t.max=4294967295
uint64_t.min=0 uint64_t.max=18446744073709551615
这里用uint32_t也可以
相关文章:

代码随想录第55天
1.判断子序列: 动态规划五部曲分析如下: 确定dp数组(dp table)以及下标的含义 dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。 注意这里是判断s是否…...
)
算法设计与分析(填空专题)
文章目录 填空题填空题 设有一稀疏图 G,则 G 采用 邻接表 存储较省空间。 算法的时间复杂性是指算法中 元运算 执行次数。 分治法的基本思想是将一个规模为 n 的问题分解为与原问题 相同 的 k 个规模较小且互相独立的子问题。 贪心算法中每次做出的贪心选择都是 当前的 最优选…...

Ubuntu22.04 K8s1.27.2
Ubuntu22.04 && K8s1.27.2 1. 服务器配置 IpServerMEM192.168.56.11k8smaster6G192.168.56.16k8snode14G192.168.56.17k8snode24G 2. 获取源 $ sudo apt-get update $ sudo apt-get install -y apt-transport-https ca-certificates curl# packages.cloud.google.c…...
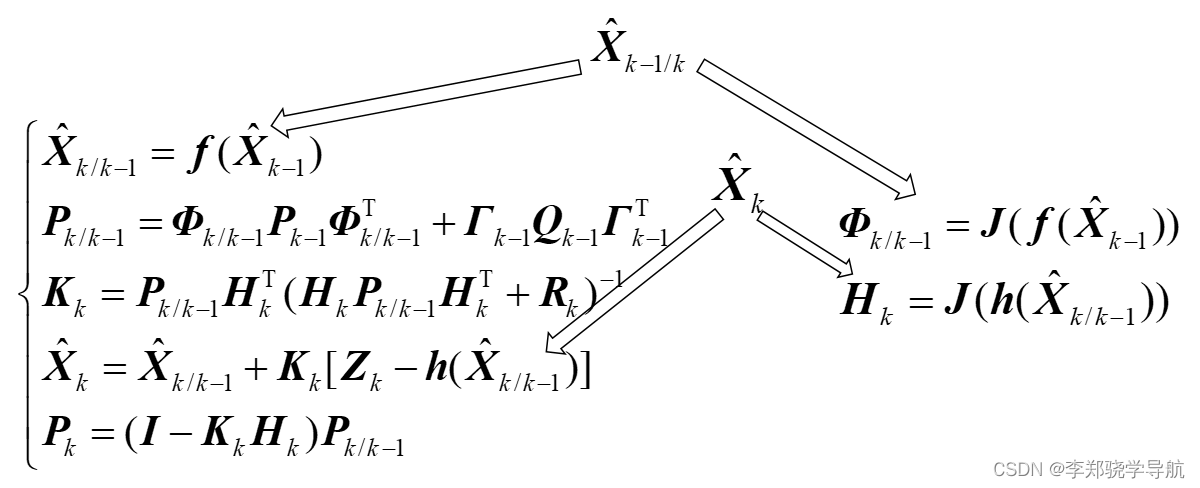
卡尔曼滤波与组合导航原理(十二)扩展卡尔曼滤波:EKF、二阶EKF、迭代EKF
文章目录 一、多元向量的泰勒级数展开二、扩展Kalman滤波三、二阶滤波四、迭代EKF滤波 一、多元向量的泰勒级数展开 { y 1 f 1 ( X ) f 1 ( x 1 , x 2 , ⋯ x n ) y 2 f 2 ( X ) f 2 ( x 1 , x 2 , ⋯ x n ) ⋮ y m f m ( X ) f m ( x 1 , x 2 , ⋯ x n ) \left\{\begin{…...
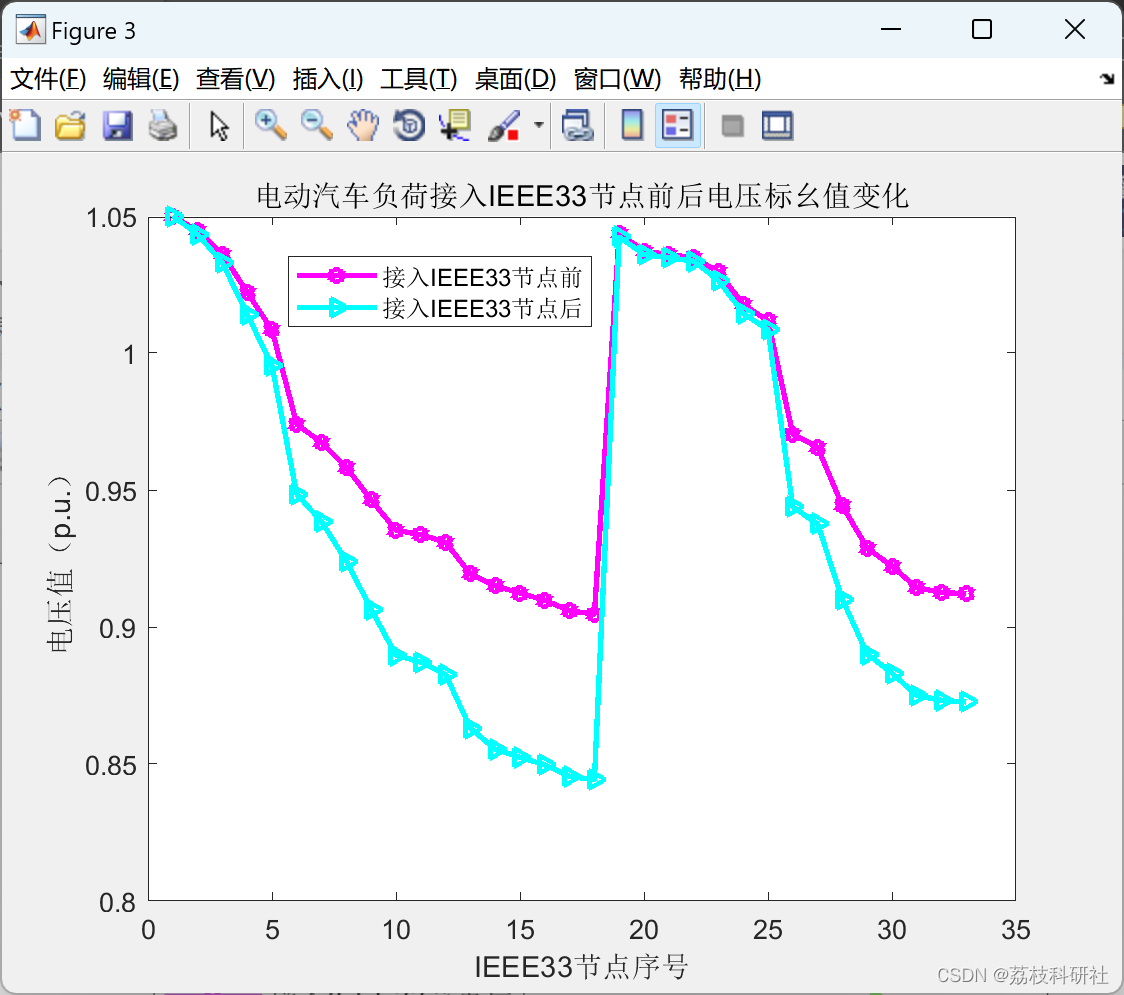
基于蒙特卡洛模拟法的电动汽车充电负荷研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
自学黑客【网络安全】,一般人我劝你还是算了吧
一、自学网络安全学习的误区和陷阱 1.不要试图先成为一名程序员(以编程为基础的学习)再开始学习 我在之前的回答中,我都一再强调不要以编程为基础再开始学习网络安全,一般来说,学习编程不但学习周期长,而…...

编程中的心理策略:如何从错误中学习并实现自我成长
在日复一日的工作中,我们免不了会产生一些失误,会因此感到沮丧和失望。但如何正确地对待和处理这些失误才是最重要的,它直接影响到我们的工作表现和个人成长。 一、面对失误而带来的指责和沮丧的策略 在程序设计领域,我们经常面临…...
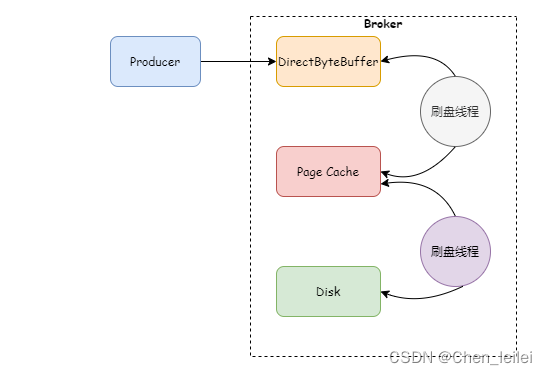
Rocket面试(五)Rocketmq发生流量控制的情况有哪些?
在使用rocketmq过程中总能看见一下异常 [TIMEOUT_CLEAN_QUEUE]broker busy, start flow control for a while, period in queue: 206ms, size of queue: 5这是因为Rocketmq出发了流量控制。 触发流量控制就是为了防止Broker压力过大挂掉。主要分为Broker流控,Consu…...

Tableau招聘信息数据可视化
获取的招聘信息数据为某招聘网站发布的大数据及数据分析相关岗位,对其他计算机相关岗位的招聘信息数据分析也有一定的参考价值。因为所获取的招聘信息数据数量只有1万左右,实际的招聘信息数量肯定不止1万,所以可能会与实际信息有一定的误差。…...
:合理应对异常)
游戏服务器开发指南(八):合理应对异常
大家好!我是长三月,一位在游戏行业工作多年的老程序员,专注于分享服务器开发相关的文章。 本文是通用程序设计主题下的第二篇。这个主题主要探讨如何编写高效、健壮、易读的游戏业务代码,每篇从一个小点切入。本次讨论的要点是&a…...

【g】聚类算法之K-means算法
聚类算法是一种无监督学习方法,它将相似的数据样本划分为一组,同时将不相似的数据样本划分为另一组。这个过程由计算机自动完成,不需要任何人为的干预。 K-means算法是一种经典的聚类算法,它的主要思想是把数据集分成k个簇&#…...
scala内建控制结构
一、条件表达式 (一)语法格式 - if (条件) 值1 else 值2(二)执行情况 条件为真,结果是值1;条件为假,结果是值2。如果if和else的返回结果同为某种类型,那么条件表达式结果也是那种类…...

Linux SSH命令实战教程,提升你的服务器管理基本功!
前言 大家好,又见面了,我是沐风晓月,本文是专栏【linux基本功-基础命令实战】的第62篇文章。 专栏地址:[linux基本功-基础命令专栏] , 此专栏是沐风晓月对Linux常用命令的汇总,希望能够加深自己的印象&am…...
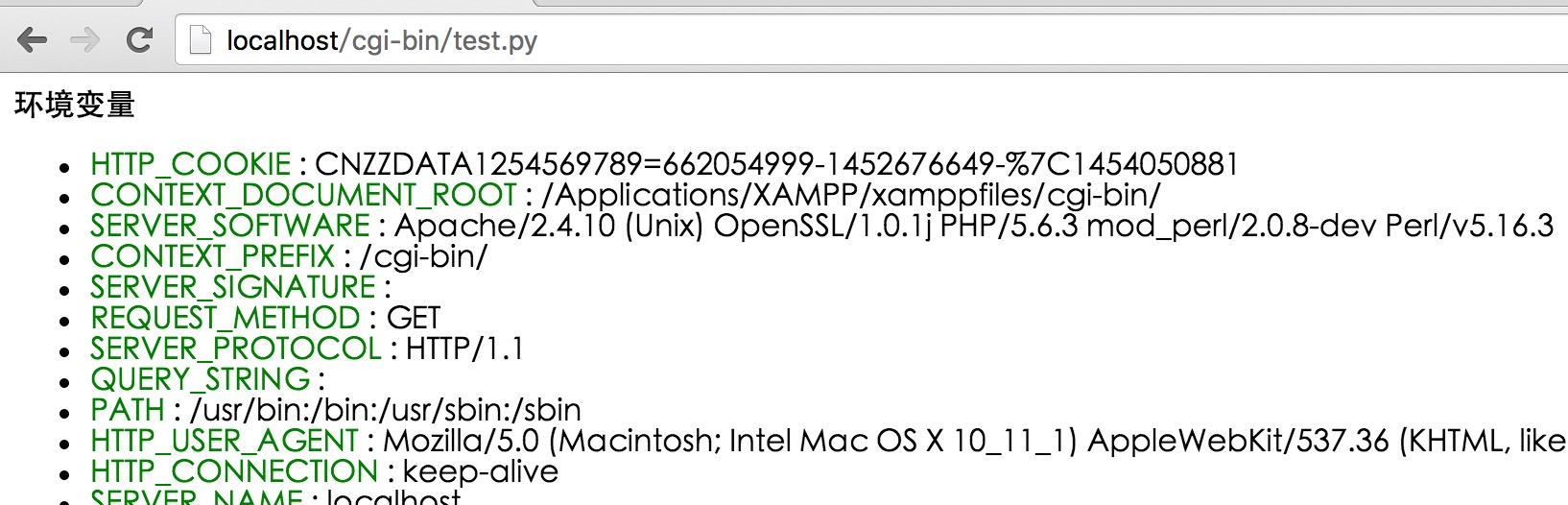
【Python】Python进阶系列教程-- Python3 CGI编程(二)
文章目录 前言什么是CGI网页浏览CGI架构图Web服务器支持及配置第一个CGI程序HTTP头部CGI环境变量GET和POST方法使用GET方法传输数据简单的表单实例:GET方法使用POST方法传递数据通过CGI程序传递checkbox数据通过CGI程序传递Radio数据通过CGI程序传递 Textarea 数据通…...

do..while、while、for循环反汇编剖析
1、循环语句重要特征提取 循环语句最重要的特点就是执行的过程中会往上跳!!! 箭头往上跳的一般都是循环语句,比如下面的for循环: 2、do..while语句反汇编 #include<iostream> using namespace std; #pragma …...

【代码随想录】刷题Day53
1.最长公共子序列 1143. 最长公共子序列 和之前的一道题目的区别就是这个子序列不需要每个字符相邻。那么条件就变成两种了,一种是当前的字符相同,一种是不同。相同跟之前的条件一样;不同则需要继承上次比较的较大值。if (text1[i - 1] tex…...

MySQL 索引及查询优化总结
一个简单的对比测试 前面的案例中,c2c_zwdb.t_file_count表只有一个自增id,FFileName字段未加索引的sql执行情况如下: 在上图中,typeall,keynull,rows33777。该sql未使用索引,是一个效率非常低…...
什么是AJAX?
AJAX是一种基于Web的技术,它允许Web应用程序在不刷新整个页面的情况下与服务器进行交互。通过AJAX,Web应用程序可以使用JavaScript向服务器发送异步请求并在不干扰用户的情况下更新页面的部分内容。 AJAX是Asynchronous JavaScript and XML的缩写。尽管…...

报表生成器FastReport .Net用户指南:显示数据列、HTML标签
FastReport .Net是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案,使用FastReport .NET可以创建独立于应用程序的.NET报表,同时FastReport .Net支持中文、英语等14种语言,可以让你的产品保证真正的国际性。 FastReport.NET官方版…...

bootstrap-dialog弹框,去掉遮盖层,可移动
1.去掉遮盖层的设置data-backdrop"false" <div class"modal fade" id"modal" aria-modal"true" role"dialog" data-backdrop"false" style"width:50%"><div class"modal-dialog modal-l…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
