Tableau招聘信息数据可视化
获取的招聘信息数据为某招聘网站发布的大数据及数据分析相关岗位,对其他计算机相关岗位的招聘信息数据分析也有一定的参考价值。因为所获取的招聘信息数据数量只有1万左右,实际的招聘信息数量肯定不止1万,所以可能会与实际信息有一定的误差。
文章目录
- 学历与经验分布柱状图
- 公司行业分布与平均薪资折柱混合图
- 公司类型分布与平均薪资折柱混合图
- 平均薪资分布折线图
- 城市平均薪资词云图
- 学历与经验平均薪资折线图
- 公司规模分布与平均薪资折线图
- 城市岗位数量散点图
学历与经验分布柱状图
不同招聘网站的侧重点不同,本数据来源的招聘网站更侧重于有经验的求职者。
招聘信息的学历要求主要为本科学历,本科学历中所需经验要求为3-5年的招聘信息最多。
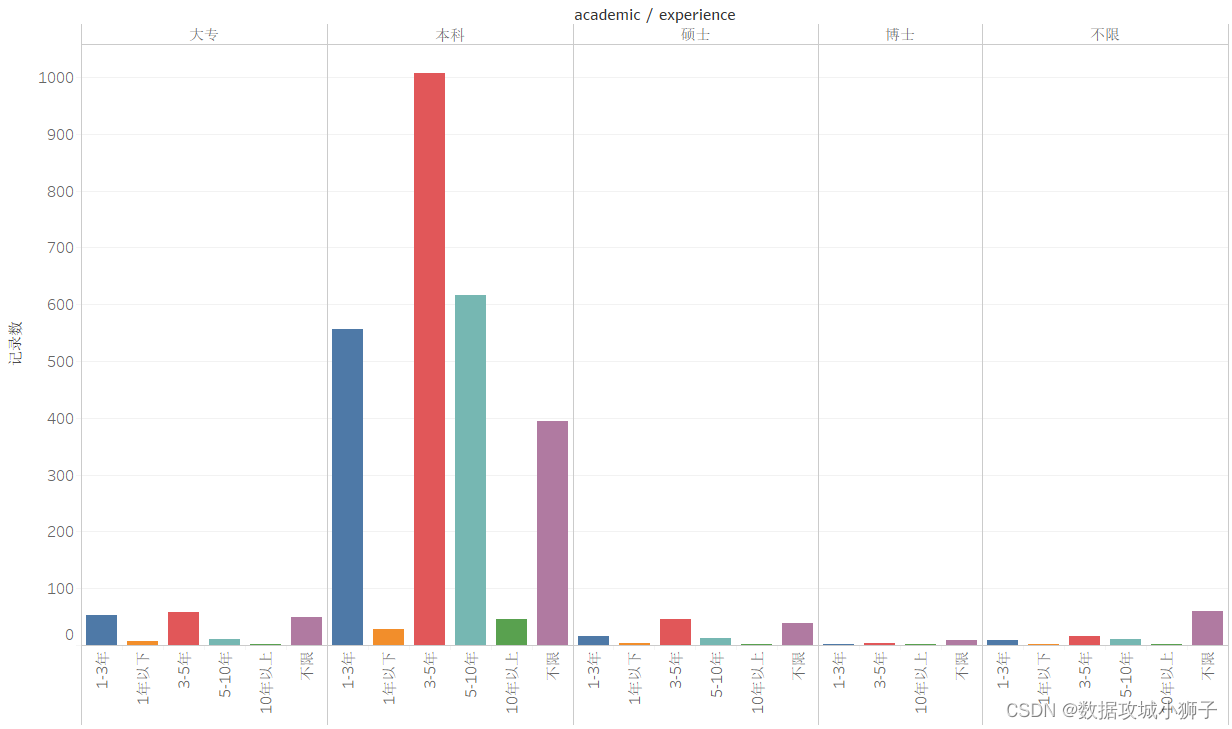
公司行业分布与平均薪资折柱混合图
数量最多的公司行业为数据服务,其次为科技金融。因为我获取的主要是大数据和数据分析相关岗位的招聘信息数据。平均薪资最高的公司行业是农林牧渔(这…可能是这个行业的几个公司发布的招聘领导级别的招聘信息),其次是新能源汽车制造。
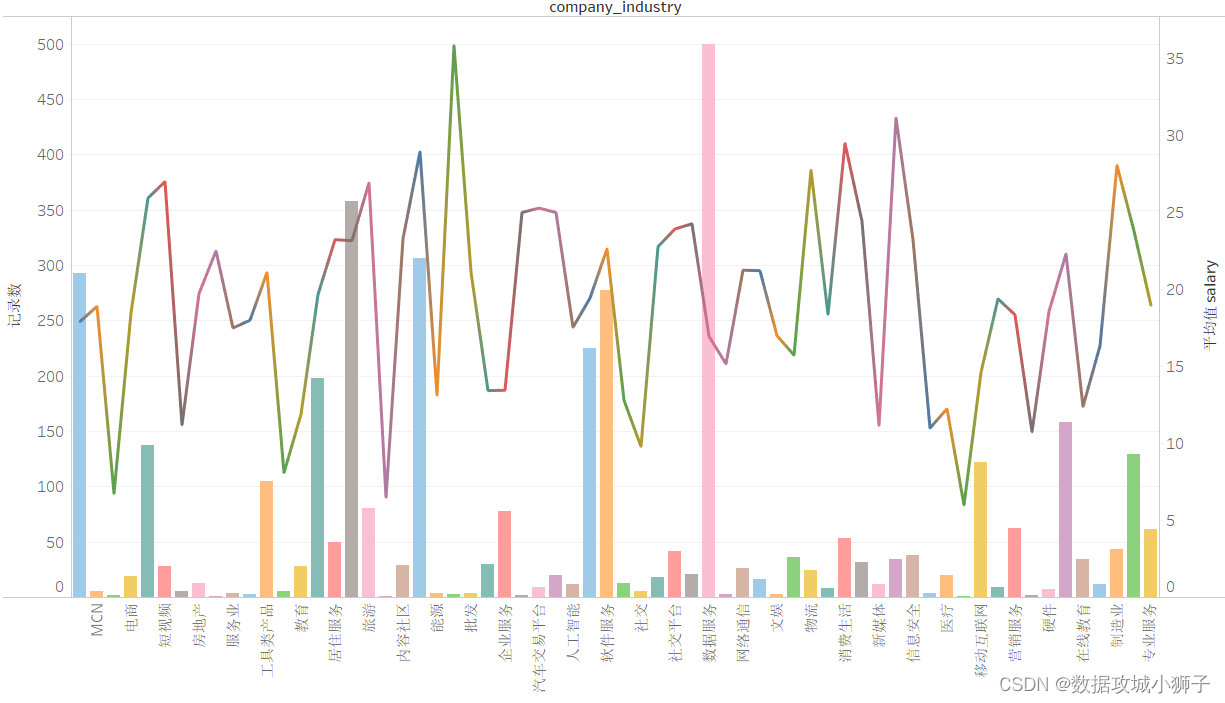
公司类型分布与平均薪资折柱混合图
不同招聘网站的公司类型划分可能不同,有的是按民营这些划分,有的是按融资这些划分。
数量最多的公司类型为不需要融资,平均薪资最高的公司类型为D轮及以上。
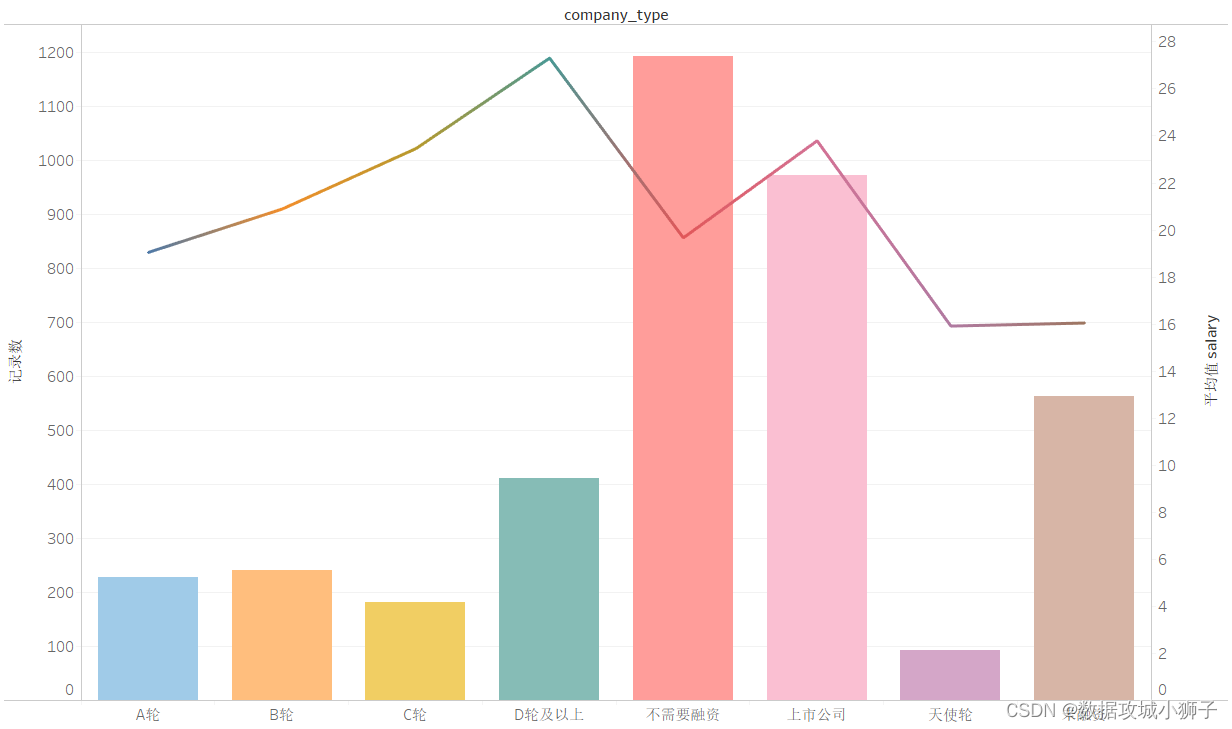
平均薪资分布折线图
平均薪资的分布折线图类似钟形曲线,平均薪资过高和过低的是少数,大部分人的薪资处于中游。招聘信息的平均薪资也和招聘网站有关,不同招聘网站的侧重点不同。从之前的学历与经验分布柱状图可以看出,招聘信息最多的是本科学历3-5年经验。所以分布较多的平均薪资区间的薪资看起来有点高。
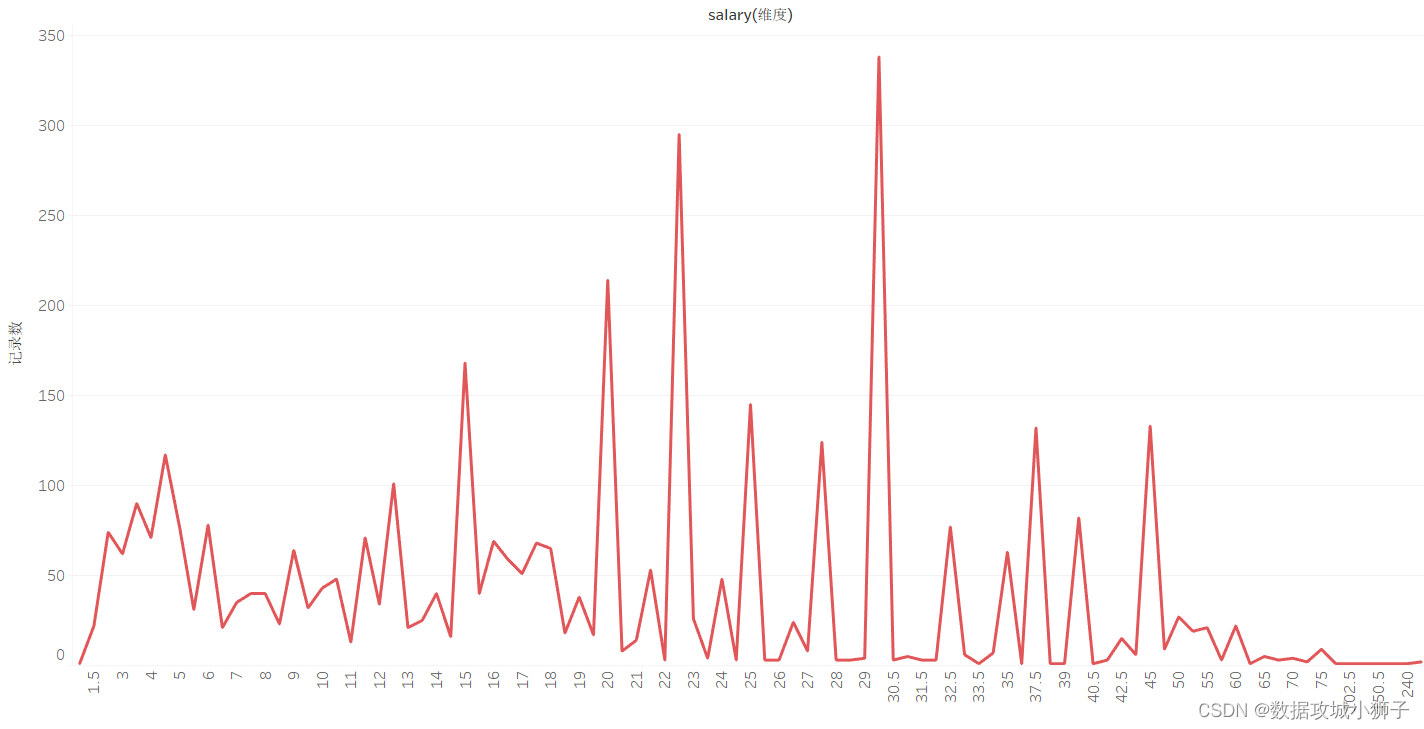
城市平均薪资词云图
各城市的平均薪资,城市的平均薪资我觉得参考价值有,但是应该不高,因为即使是互联网行业发展一般的城市可能主要招聘有经验的领导岗位,这些岗位会提高城市的平均薪资。

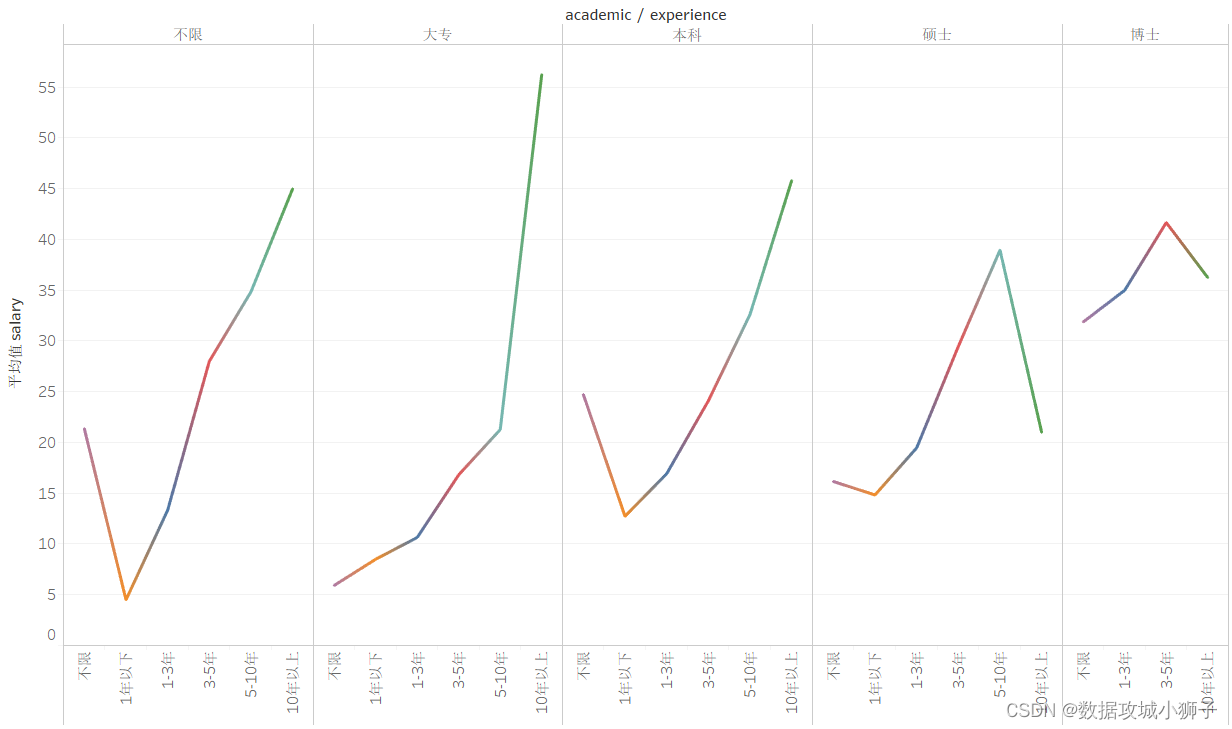
学历与经验平均薪资折线图
这个图就很容易看出各学历随着工作经验的增多,平均薪资也随着增多。当然也存在一些不合理的地方,准确的可视化图表需要大量准确数据的支持,我获取的数据虽然有1万条,但是在如今的大数据时代,说实话还是比较少的。
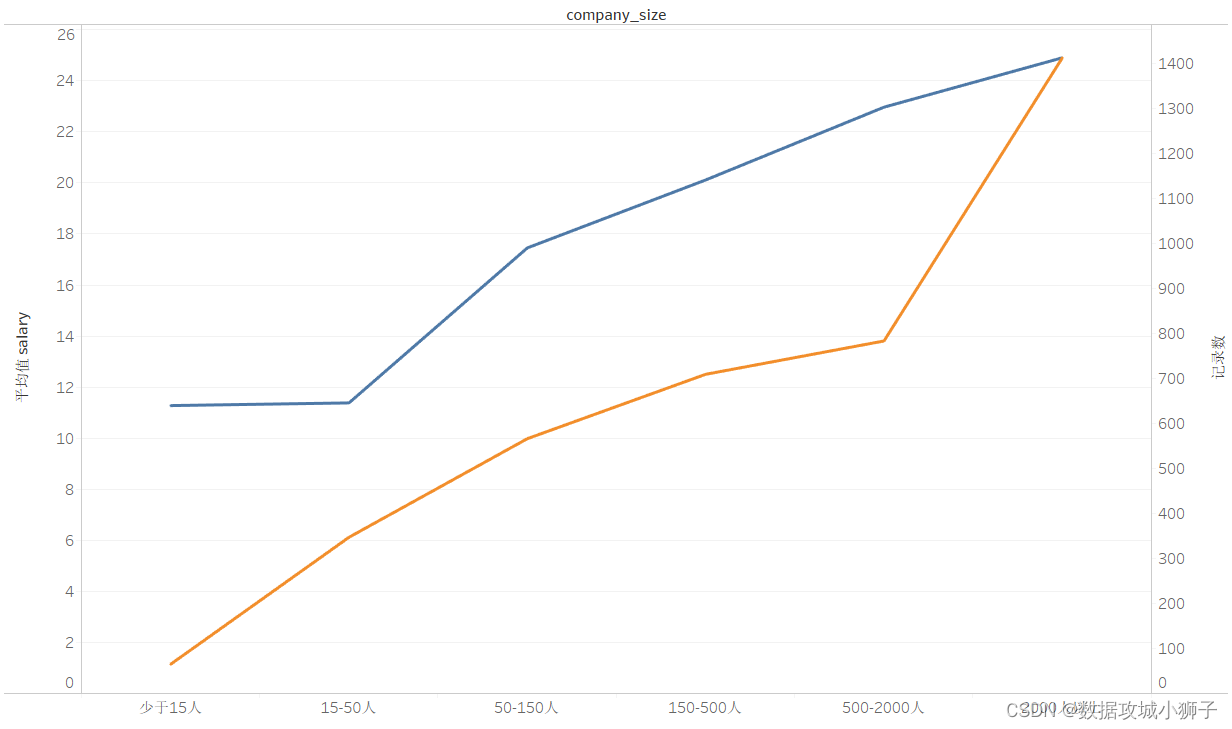
公司规模分布与平均薪资折线图
这个图就比较合理,公司规模的数量和平均薪资随着公司规模的增多而增多。
城市岗位数量散点图
招聘岗位的所在城市主要位于沿海地区城市及各省会城市,其他未标出的城市不是没有发布招聘信息,而是因为我获取的数据不全面,还望理解。

招聘信息的数据可视化分析其实并不复杂,有的数据需要进行更复杂的计算,所以不断学习,不断进步吧!
相关文章:

Tableau招聘信息数据可视化
获取的招聘信息数据为某招聘网站发布的大数据及数据分析相关岗位,对其他计算机相关岗位的招聘信息数据分析也有一定的参考价值。因为所获取的招聘信息数据数量只有1万左右,实际的招聘信息数量肯定不止1万,所以可能会与实际信息有一定的误差。…...
:合理应对异常)
游戏服务器开发指南(八):合理应对异常
大家好!我是长三月,一位在游戏行业工作多年的老程序员,专注于分享服务器开发相关的文章。 本文是通用程序设计主题下的第二篇。这个主题主要探讨如何编写高效、健壮、易读的游戏业务代码,每篇从一个小点切入。本次讨论的要点是&a…...

【g】聚类算法之K-means算法
聚类算法是一种无监督学习方法,它将相似的数据样本划分为一组,同时将不相似的数据样本划分为另一组。这个过程由计算机自动完成,不需要任何人为的干预。 K-means算法是一种经典的聚类算法,它的主要思想是把数据集分成k个簇&#…...
scala内建控制结构
一、条件表达式 (一)语法格式 - if (条件) 值1 else 值2(二)执行情况 条件为真,结果是值1;条件为假,结果是值2。如果if和else的返回结果同为某种类型,那么条件表达式结果也是那种类…...

Linux SSH命令实战教程,提升你的服务器管理基本功!
前言 大家好,又见面了,我是沐风晓月,本文是专栏【linux基本功-基础命令实战】的第62篇文章。 专栏地址:[linux基本功-基础命令专栏] , 此专栏是沐风晓月对Linux常用命令的汇总,希望能够加深自己的印象&am…...
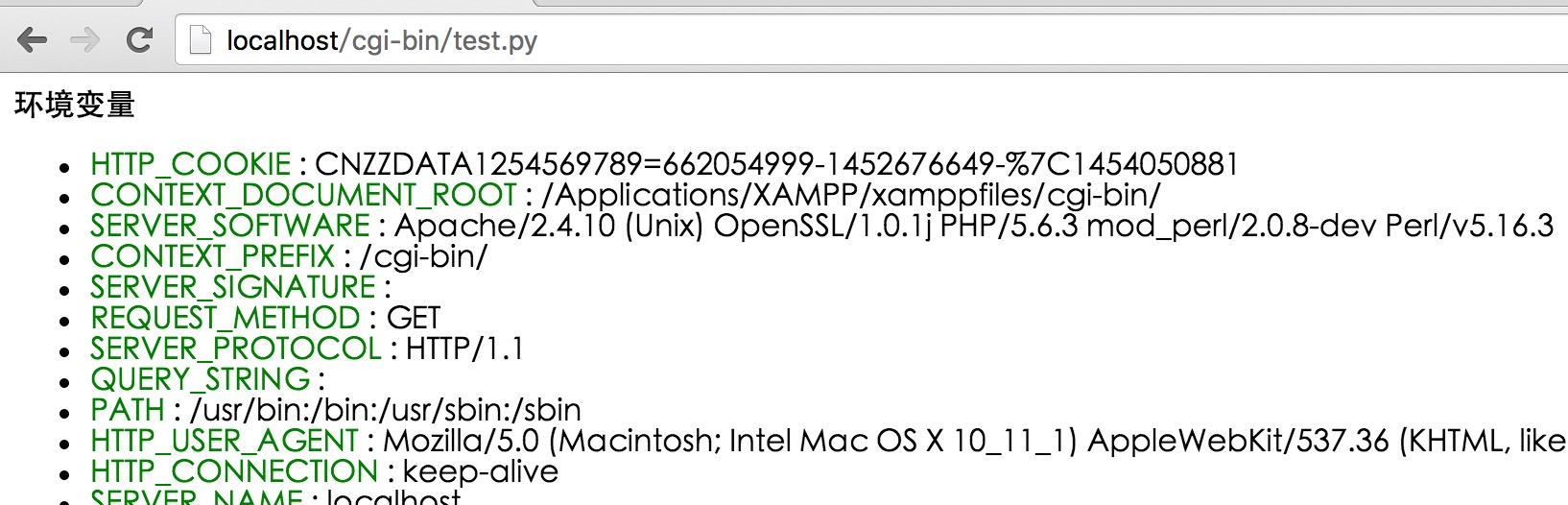
【Python】Python进阶系列教程-- Python3 CGI编程(二)
文章目录 前言什么是CGI网页浏览CGI架构图Web服务器支持及配置第一个CGI程序HTTP头部CGI环境变量GET和POST方法使用GET方法传输数据简单的表单实例:GET方法使用POST方法传递数据通过CGI程序传递checkbox数据通过CGI程序传递Radio数据通过CGI程序传递 Textarea 数据通…...

do..while、while、for循环反汇编剖析
1、循环语句重要特征提取 循环语句最重要的特点就是执行的过程中会往上跳!!! 箭头往上跳的一般都是循环语句,比如下面的for循环: 2、do..while语句反汇编 #include<iostream> using namespace std; #pragma …...

【代码随想录】刷题Day53
1.最长公共子序列 1143. 最长公共子序列 和之前的一道题目的区别就是这个子序列不需要每个字符相邻。那么条件就变成两种了,一种是当前的字符相同,一种是不同。相同跟之前的条件一样;不同则需要继承上次比较的较大值。if (text1[i - 1] tex…...

MySQL 索引及查询优化总结
一个简单的对比测试 前面的案例中,c2c_zwdb.t_file_count表只有一个自增id,FFileName字段未加索引的sql执行情况如下: 在上图中,typeall,keynull,rows33777。该sql未使用索引,是一个效率非常低…...
什么是AJAX?
AJAX是一种基于Web的技术,它允许Web应用程序在不刷新整个页面的情况下与服务器进行交互。通过AJAX,Web应用程序可以使用JavaScript向服务器发送异步请求并在不干扰用户的情况下更新页面的部分内容。 AJAX是Asynchronous JavaScript and XML的缩写。尽管…...

报表生成器FastReport .Net用户指南:显示数据列、HTML标签
FastReport .Net是一款全功能的Windows Forms、ASP.NET和MVC报表分析解决方案,使用FastReport .NET可以创建独立于应用程序的.NET报表,同时FastReport .Net支持中文、英语等14种语言,可以让你的产品保证真正的国际性。 FastReport.NET官方版…...

bootstrap-dialog弹框,去掉遮盖层,可移动
1.去掉遮盖层的设置data-backdrop"false" <div class"modal fade" id"modal" aria-modal"true" role"dialog" data-backdrop"false" style"width:50%"><div class"modal-dialog modal-l…...

7. user-Agent破解反爬机制
文章目录 1. 为什么要设置反爬机制2. 服务器如何区分浏览器访问和爬虫访问3. 反爬虫机制4. User-Agent是什么5. 如何查询网页的User-Agent6. user-agent信息解析7. 爬虫程序user-agent和浏览器user-agent的区别8. 代码查看爬虫程序的user-agent9. 在代码中加入请求头信息 1. 为…...

3.Nginx+Tomcat负载均衡和动静分离群集
文章目录 NginxTomcat负载均衡和动静分离群集Nginx作用实验七层反向代理nginx动静分离四层反向代理负载均衡 NginxTomcat负载均衡和动静分离群集 Nginx是-款非常优秀的HTTP服务器软件 支持高达50 000个并发连接数的响应拥有强大的静态资源处理能力运行稳定内存、CPU等系统资源…...
数据结构与算法之树结构
目录 为什么要使用树结构树结构基本概念树的种类树的存储与表示常见的一些树的应用场景为什么要使用树结构 线性结构中不论是数组还是链表,他们都存在着诟病;比如查找某个数必须从头开始查,消耗较多的时间。使用树结构,在插入和查找的性能上相对都会比线性结构要好 树结构…...

【python】 用来将对象持久化的 pickle 模块
pickle 模块可以对一个 Python 对象的二进制进行序列化和反序列化。说白了,就是它能够实现任意对象与二进制直接的相互转化,也可以实现对象与文本之间的相互转化。 比如,我程序里有一个 python 对象,我想把它存到磁盘里ÿ…...

【博客654】prometheus配置抓取保护以防止压力过载
prometheus抓取保护配置以防止压力过载 场景 担心您的应用程序指标可能突然激增,以及指标突然激增导致prometheus压力过载 就像生活中的许多事情一样,标签要有节制。当带有用户 ID 或电子邮件地址的标签被添加到指标时,虽然它不太可能结束…...

Backtrader官方中文文档:第十三章Observers观察者
本文档参考backtrader官方文档,是官方文档的完整中文翻译,可作为backtrader中文教程、backtrader中文参考手册、backtrader中文开发手册、backtrader入门资料使用。 本章包含 backtrader 官方Observers章节全部内容,入口 : https://backtrader.com/docu/observers-and-sta…...

算法leetcode|54. 螺旋矩阵(rust重拳出击)
文章目录 54. 螺旋矩阵:样例 1:样例 2:提示: 分析:题解:rust:go:c:python:java:每次循环移动一步:每次循环完成一个顺时针:…...
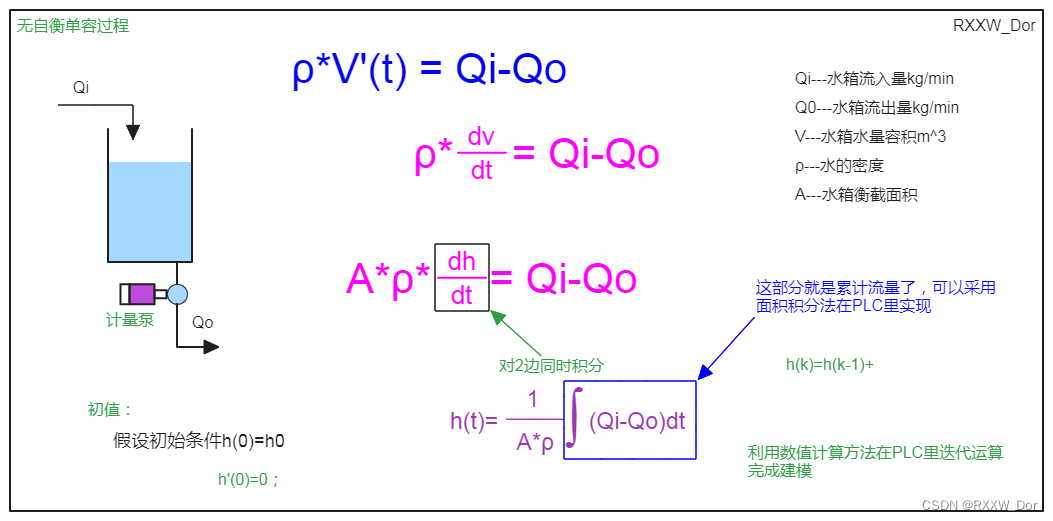
单容水箱建模(自衡单容水箱+无自衡单容水箱)
自衡单容水箱Simulink建模和PLC源代码请参看下面文章链接: 单容双容水箱建模(simulink仿真+PLC代码)_RXXW_Dor的博客-CSDN博客PLC通过伯努利方程近似计算水箱流量详细内容请参看下面的文章博客PLC通过伯努利方程近似计算水箱流量(FC)_怎么用伯努利方程求某水位流量_RXXW_Dor的…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
