CSDN竞赛57期题解
总结
交卷时一看才六十多分还有点吃惊,一看非编程题部分还是丢了二十分。填空题是这类竞赛最大的诟病,答案是名词的必然不唯一,答案需要计算的给定的参考答案必然计算错误,更离谱的是题目出成这样,反馈后官方竟然一点改变的意思都没有。但凡答案不唯一的题目你给多个候选答案也不会被人这么吐槽了。寄存器与状态寄存器、图灵机与图灵机模型这种不唯一的答案还记忆犹新,多少期前反馈时,C站不想着手动改一下判错的答案,而是回复以后不会再出填空题了,然而仅隔了一期填空题又再现了。
为什么这类竞赛的赞助商这么钟爱填空题呢?比如这次填空题答案是BST,看到题目时候我就在群里艾特出题人,BST至少有三种中文叫法,你想让我们填哪种?还特地翻了下书,没找着书上的叫法,于是在二叉搜索树、二叉排序树、二叉查找书当中选了个最常见的二叉搜索树填上去了,果不其然答案是二叉排序树,十分丢失。
另一道扣分的是判断题,问树的等价二叉树是不是唯一的,我寻思按照正常的转换方法应该是唯一的,结果却不是。失分的两题在书上也都没翻到解答。回到开始的问题,为什么赞助商总是出这种让人反感的填空题,他们的回复是以书上答案为准。提供了赞助,用这种方式迫使我们买本书不过分吧。还是随遇而安,叫不醒装睡的人,能白嫖本书也不亏。
编程题部分几乎该类竞赛每期都出现了不给数据规模的情况,可以发现出题人相当的不专业,python选手用map切分下就好了,C++选手每次写之前还要手动处理下输入数组,很是烦人。另外这次的两道题都不给数据范围,全靠自己猜范围了。
题目列表
1.凑数
题目描述
给定一组n个正整数,要求每次选其中一个数乘以或除以一个素数(称为一次凑数),问至少需要凑数多少次可以把所有的数都凑成相等。
分析
将所有数凑成相等第一反应是凑成最小公倍数或者最大公约数。但是这种方式的解很容易被推翻,比如2 4 8,凑成2和8的操作次数都是3,但是凑成4的次数是2,那么4这个数有什么性质呢?显然作为最终凑成的数,数组中小于它的数一定是它的约数,大于它的数一定是它的倍数。所以我们可以暴力求解一波,先列出一波候选解,除了数组里每个元素,还有就是它们的最大公约数和最小公倍数。可以先打表求出正向前 i i i个元素的最小公倍数 x x x以及逆向后 n − i n - i n−i个元素的最大公约数 y y y,如果 x x x 能被 y y y整除就尝试将 x x x和 y y y作为候选解求下凑的次数,最后取个最小值就可以了。
当然比赛时我没有这么做,秉着最大得分原则,读完题就想着先混个部分分,求出所有数的最大公约数 t t t,然后求所有数到 t t t需要操作的次数之和。提交通过了大部分用例,数据范围改到十万再提交就AC了,可见这个题目的数据还是比较水的,有点数论基础的同学都可以比较快的AC。
代码
#include <iostream>
#include <string>
using namespace std;
int a[100005];
int gcd(int a, int b) {return b ? gcd(b, a % b) : a;
}
int get(int n) {int res = 0;for(int i = 2; i <= n; i++) {while(n % i == 0) {n /= i;res++;}}return res;
}
int main() {string s;getline(cin,s);int n = 0;int t = 0;int sz = s.size();for(int i = 0; i < sz; i++) {if (s[i] != ' ') t = t * 10 + s[i] - '0';else {a[n++]=t;t = 0;}}a[n++] = t;t = a[0];for (int i = 1; i < n; i++) {t = gcd(t, a[i]);}int res = 0;for(int i = 0; i < n; i++) {int r = a[i] / t;res += get(r);}cout<<res<<endl;return 0;
}
2.树的寻路
题目描述
给定一棵有n个节点且节点编号为1到n的树,求满足以下条件的路径组合数: 1. 从节点a到节点b的路径(称为路径ab) 边数为p 2. 从节点c到节点d的路径(称为路径cd)边数为q 3. 路径ab和cd不交,即不存在一个节点既在路径ab又在路径 cd上
分析
这类题目早几年做应该是可以秒掉的,工作躺平太久加之下班比较困了,花了挺长时间才通过四成用例。首先题目用例给了三条边,结果是8,没有用例说明还是让人很疑惑的,毕竟组合数这个词比较模糊。用例是1到2,2到3,3到4这三条边,乍一看不就1-2和3-4这两个长度为1的边不相交嘛,就算再倒过来算上3-4和1-2也才两种组合数啊,8是怎么得到的?不妨尝试去枚举一下路径的起点,第一条路径的起点可以是1 2 3 4,可以得到以下的路径组合:
- 1-2,3-4
- 1-2,4-3
- 2-1,3-4
- 2-1,4-3
- 3-4,1-2
- 3-4,2-1
- 4-3,1-2
- 4-3,2-1
虽然看起来这些组合有点离谱,就两条路径弄出了八个组合,但是用例来看应该就是这种组合方式了。
想象一下作为一棵树,其中的任意一个节点作为路径的起点,路径可以向其孩子节点延伸,也可以向其祖先节点延伸,也可以通过祖先节点向其兄弟、表兄弟节点延伸,我们选定一个根节点来遍历是没有什么意义的。
不妨先建个图,然后像上面枚举路径起点那样去枚举路径长度为 x x x路径的起点,遍历到其中一条长度为 x x x的路径的终点时,要保证遍历途中的节点做好了标记。再遍历下所有节点,只要没被标记的节点都可以作为与长度为 x x x路径不相交的、长度为 y y y的路径的起点。再次以新的起点去遍历相邻节点,直到找到与第一条路径不相交的路径,就将方案数加上1。
dfs过程中要注意遇见被标记的节点不可继续拓展,因为要么是第二条路径遍历的时候遇见的第一条路径上的节点,要么就是父节点,从 a a a走到 b b b,显然不能再走回来了。
这题没有给定数据范围,比赛时就假定数据范围是1w了,题目评测是一旦有超时的用例就是TLE,一分没有。所以加了下数据规模超过一千的就输出0。当然直接输出0也能得到一成的分数。比赛时由于时间关系没有继续调整数据范围和TLE的界限的,不然应该可以通过更多的用例。
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10005, M = 2 * N;
int idx = 0,e[M],ne[M],h[N];
int n,x,y,ans = 0;
int st[N];
void add(int a,int b) {e[idx]=b, ne[idx]=h[a],h[a] = idx++;
}
void dfs(int u, int d, int t) {if (!t) {//枚举的是第一条路径if (d == x) {//路径长度达到xfor(int i = 1; i <= n; i++) {if (!st[i]) {//枚举第二条路径的起点st[i] = true;dfs(i, 0, 1);st[i] = false;}}return;}} else {//枚举的是第二条路径if (d == y) {//第二条路径长度达到yans++;return;}}for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];//已经被标记的节点跳过if (st[j]) continue;st[j] = true;dfs(j, d + 1, t);st[j] = false;}
}
int main() {cin>>n>>x>>y;memset(h,-1,sizeof h);for(int i = 1; i < n; i++) {int a,b;cin>>a>>b;add(a,b);add(b,a);}if (n > 1000) {cout<<0<<endl;return 0;}for(int i = 1; i <= n; i++) {st[i] = true;//枚举长度为x的路径起点idfs(i, 0, 0);st[i] = false;}cout<<ans<<endl;return 0;
}
相关文章:

CSDN竞赛57期题解
总结 交卷时一看才六十多分还有点吃惊,一看非编程题部分还是丢了二十分。填空题是这类竞赛最大的诟病,答案是名词的必然不唯一,答案需要计算的给定的参考答案必然计算错误,更离谱的是题目出成这样,反馈后官方竟然一点…...
springboot+vue.js大学生竞赛报名作品评分管理系统
本文介绍了大学生竞赛管理系统的开发全过程。通过分析大学生竞赛管理系统管理的不足,创建了一个计算机管理大学生竞赛管理系统的方案。文章介绍了大学生竞赛管理系统的系统分析部分,包括可行性分析等,系统设计部分主要介绍了系统功能设计和数…...

Python爱好者的自我修养(1):简单输入与输出
Python简单输入与输出 1.输出1.1 简单输出1.2 转义字符1.2.1 定义1.2.2 常见的转义字符用法 2.输入3.温馨提示 终于…… 终于…… 我开始玩Python了 (不是C不学了哈,C还是照更~) 今天先来简单讲下输入和输出 1.输出 1.1 简单输出 输出的函…...
java SSM 摄影作品网站myeclipse开发mysql数据库springMVC模式java编程计算机网页设计
一、源码特点 java SSM 摄影作品网站系统是一套完善的web设计系统(系统采用SSM框架进行设计开发,springspringMVCmybatis),对理解JSP java编程开发语言有帮助,系统具有完整的源代 码和数据库,系统主要采…...

[Maven高级]->近万字文章带你深入了解Maven
⭐作者介绍:大二本科网络工程专业在读,持续学习Java,努力输出优质文章 ⭐作者主页:逐梦苍穹 ⭐所属专栏:JavaEE ⭐如果觉得文章写的不错,欢迎点个关注一键三连😉有写的不好的地方也欢迎指正&…...

物联网Lora模块从入门到精通(五)光照与温湿度传感器
一、前言 在程序开发中,光照与温湿度的获取是十分常见与重要的,本文我们主要是使用M21温湿度光照三合一传感器,其中温湿度数据通过协议获取,而光照通过ADC获取。 二、代码实现 本文内容较为简单,且后续文章将在本文基…...

【网络编程】计算机网络基础知识总结 | 运输层 |TCP协议
文章目录 前言一、计算机网络层次结构二、网络层三、运输层3.1、TCP/IP协议介绍3.2、端口(协议端口号)3.3、套接字3.4、TCP实现原理3.4.1、TCP的特点3.4.2、停止等待协议3.4.3、滑动窗口协议3.4.4、拥塞控制3.4.5、TCP连接的三个阶段 3.5、UDP实现原理 前…...

python关键知识点
1. 变量:在程序中存储值或对象的名称。 2. 数据类型:指变量的数据类型,例如 str、int、float、list、tuple、dict、set 等。 3. 操作符:表示运算符号,例如加号 和减号 -。 4. 循环:通过重复执行某个代码…...

c# 从零到精通 数组的操作-将两个一维数组合并成一个二维数组
c# 从零到精通 数组的操作-将两个一维数组合并成一个二维数组 using System; using System.Collections.Generic; using System.Linq; using System.Text; namespace Test07 { class Program { static void Main(string[] args) { //定义两个一维数组 int[] arr1 new int[] {…...
Linux目录结构(与window目录结构对比+绝对路径和相对路径)
一、Linux目录结构 Linux目录结构是一个标准化的文件系统层次结构,非常有组织性并且易于管理。而与Windows 操作系统不同,Linux将所有文件和设备都组织在一个单一的根目录下。以下是Linux的标准目录结构: /:根目录,包含…...
投票活动小程序开发搭建
由于小程序是基于微信开发者工具编写的,因此我先介绍一下需要使用的工具和技术: - 微信开发者工具:用于开发、调试和发布小程序。 - 小程序云开发:用于存储数据和进行后端逻辑处理。 - uni-app框架:uni-app 是一个使…...

代码随想录day18
513.找树左下角的值 本题用前中后序都可以(都是先遍历左再遍历右,保证最后一定是左侧的节点),因为没有中节点的处理逻辑,用全局变量记录最大深度,只要遇到叶子结点并且当前深度比最大深度大,就更…...
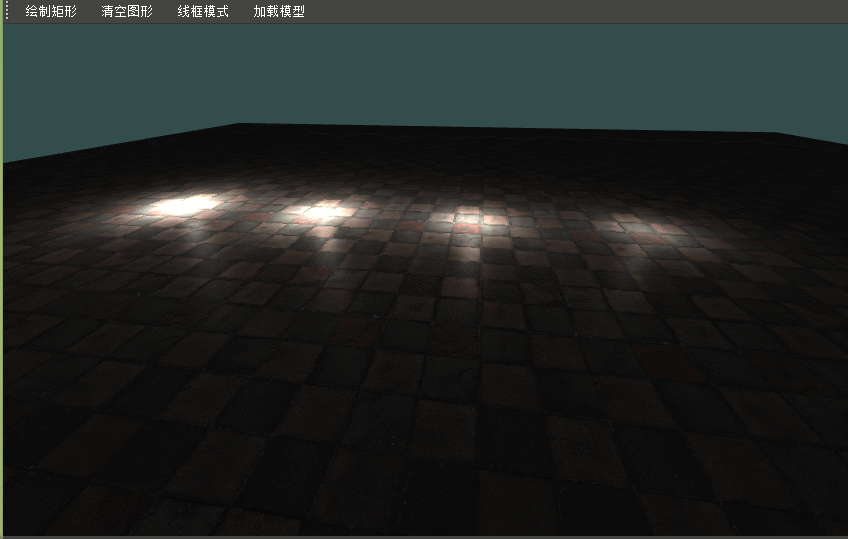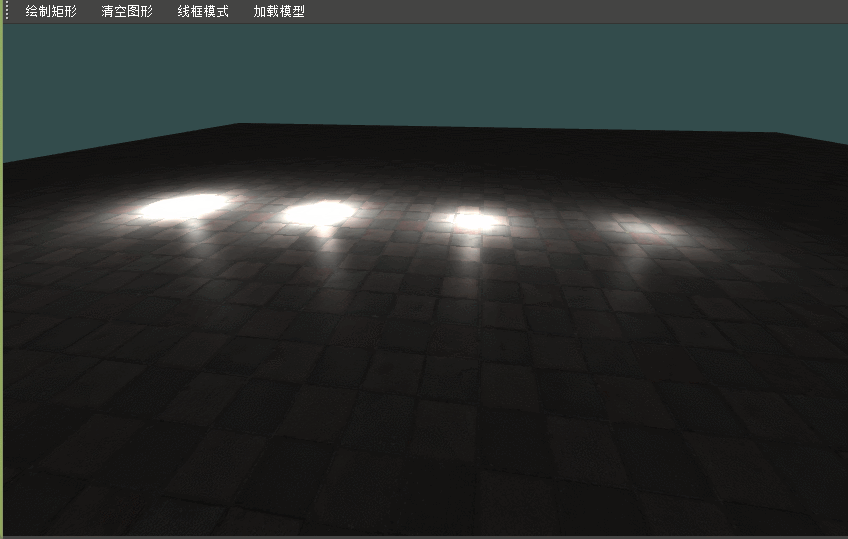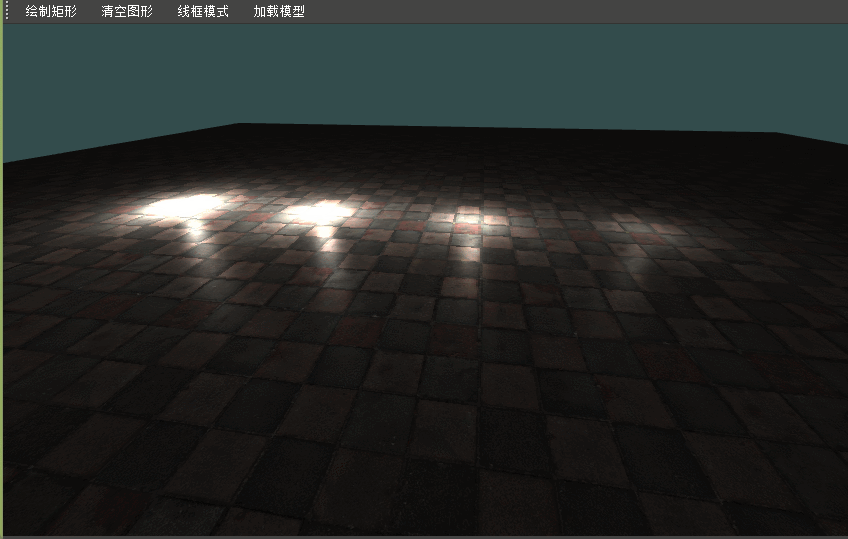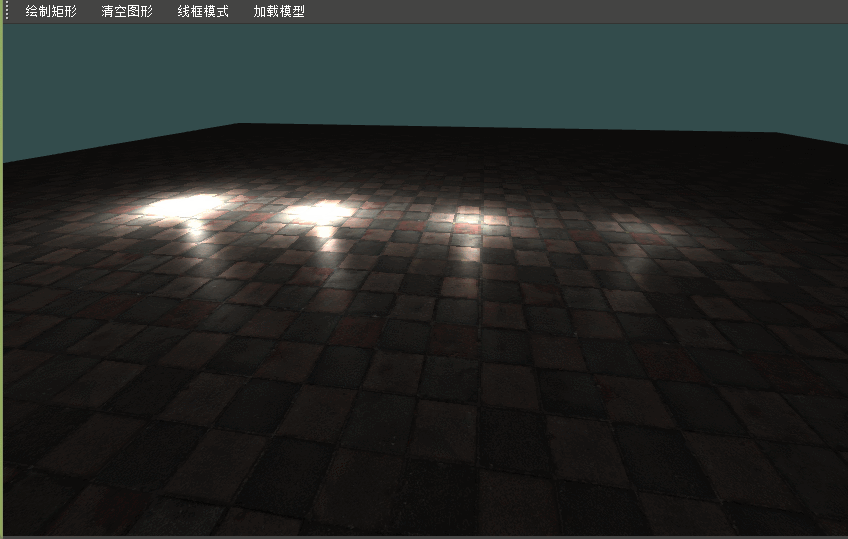
QT+OpenGL高级光照 Blinn-Phong和Gamma校正
QTOpenGL高级光照1 本篇完整工程见gitee:QtOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主 Blinn-Phong 冯氏光照:视线与反射方向之间的夹角不小于90度,镜面光分量会变成0.0(不是很合理&am…...
【Ubuntu系统内核更新与卸载】
【Ubuntu系统内核更新与卸载】 1. 前言2. 内核安装2.1 系统更新2.2 官网下载 3. 内核卸载3.1 需求分析3.2 卸载方法 1. 前言 我们在搭建环境时常常遇到内核版本不匹配的问题,需要我们安装新的内核版本;有时又会遇到在安装软件时报错boot空间已满无法安装…...
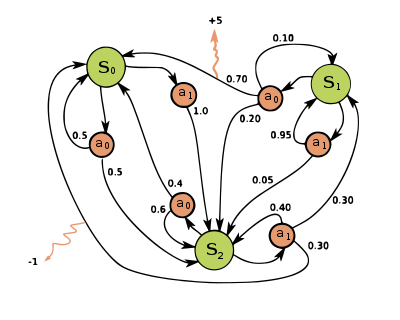
RL - 强化学习 马尔可夫奖励过程 (MRP) 的状态价值
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/131084795 GitHub 源码: https://github.com/SpikeKing/Reinforcement-Learning-Algorithm 马尔可夫奖励过程 (MRP) 的状态价值是指在某…...

Mybatis之批处理流式查询
文章目录 1 批处理查询1.1 引言1.2 流式查询1.2.1 定义1.2.2 流式查询接口1.2.3 使用流式查询关闭问题1.2.3.1 SqlSessionFactory1.2.3.2 TransactionTemplate1.2.3.3 Transactional 注解 1.2.4 完整示例1.2.4.1 mapper接口和SQL1.2.4.2 Service操作 1.3 游标查询1.3.1 定义1.3…...
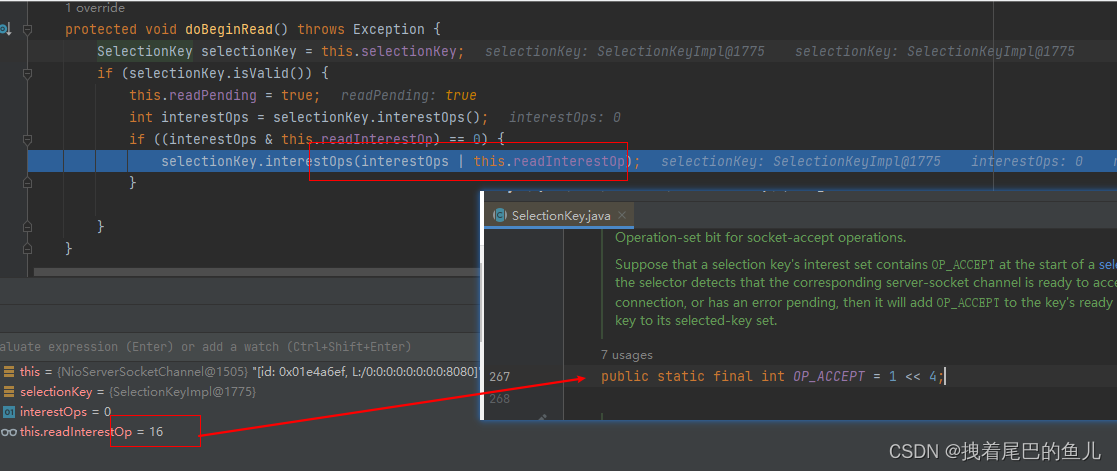
Spring架构篇--2.7.3 远程通信基础--Netty原理--bind实现端口的绑定
前言:在对ServerBootstrap 进行属性赋值之后,通过bind 方法完成端口的绑定,并开始在NioEventLoop中进行轮询进行事件的处理;本文主要探究ServersocketChannel 在netty 中是如何完成注册,以及端口的绑定 1 Nio selecto…...

【改进的多同步挤压变换】基于改进多同步挤压的高分辨率时频分析工具,用于分析非平稳信号(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

有关 python 切片的趣事
哈喽大家好,我是咸鱼 今天来讲一个我在实现 python 列表切片时遇到的趣事 在正式开始之前,我们先来了解一下切片(slice) 切片操作是访问序列(列表、字符串…)中元素的另一种方法,它可以访问一…...

ChatGPT 会带来失业潮吗?
(永久免费,扫码加入) 最近在翻知乎上的一些文章,很多都是跟ChatGPT有关的。因为本身是搞Python编程的,知乎推荐系统给我推荐了一篇廖雪峰老师的文章,觉得很有意思。 一共1119个赞,还是很厉害的&…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
