【基础知识整理】图的基本概念 邻接矩阵 邻接表
一、图概述
定义:
图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的;
其中,点通常被成为"顶点(vertex)“,而点与点之间的连线则被成为"边或弧”(edege)。
通常记为,G=(V,E)。
图是一种重要的数据结构,基本概念包括:顶点,边,有向,无向,权,路径回路,连通域,邻接点,度,入边,出边,入度,出度等等,很好理解。
参考这篇博客:http://www.cnblogs.com/skywang12345/p/3691463.html
二、图基础
2 图的分类
根据边是否有方向,将图可以划分为:无向图和有向图。
2.1.1 无向图
即两个顶点之间没有明确的指向关系,只有一条边相连,例如,A顶点和B顶点之间可以表示为 <A, B> 也可以表示为<B, A>,如下所示
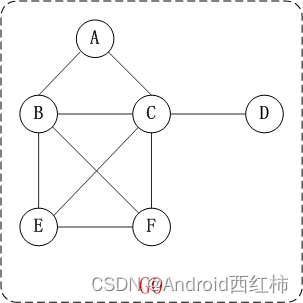
上面的图G0是无向图,无向图的所有的边都是不区分方向的。
我们用 **图 = (顶点集合,{边集合})**来表示图。
G0=(V1,{E1}) 其中,
(01) V1={A,B,C,D,E,F}。 V1表示由"A,B,C,D,E,F"几个顶点组成的集合。
(02) E1={(A,B),(A,C),(B,C),(B,E),(B,F),(C,F), (C,D),(E,F),(C,E)}。 E1是由边(A,B),边(A,C)…等等组成的集合。其中,(A,C)表示由顶点A和顶点C连接成的边。
2.2.2 有向图
顶点之间是有方向性的,例如A和B顶点之间,A指向了B,B也指向了A,两者是不同的,如果给边赋予权重,那么这种异同便更加显著了
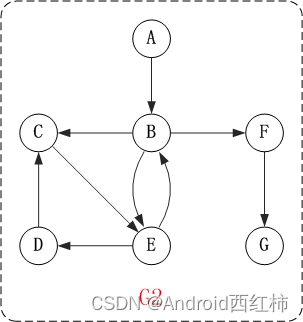
上面的图G2是有向图。
和无向图不同,有向图的所有的边都是有方向的!
3、邻接点和度
3.1 邻接点
一条边上的两个顶点叫做邻接点。
例如,上面无向图G0中的顶点A和顶点C就是邻接点。
在有向图中,除了邻接点之外;还有"入边"和"出边"的概念。
顶点的入边,是指以该顶点为终点的边。而顶点的出边,则是指以该顶点为起点的边。
例如,上面有向图G2中的B和E是邻接点;<B,E>是B的出边,还是E的入边。
3.2 度
在无向图中,某个顶点的度是邻接到该顶点的边(或弧)的数目。
例如,上面无向图G0中顶点A的度是2。
在有向图中,度还有"入度"和"出度"之分。
某个顶点的入度,是指以该顶点为终点的边的数目。
而顶点的出度,则是指以该顶点为起点的边的数目。顶点的度=入度+出度。
例如,上面有向图G2中,顶点B的入度是2,出度是3;顶点B的度=2+3=5。
4、路径和回路
路径:如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
路径长度:路径中"边的数量"。
简单路径:若一条路径上顶点不重复出现,则是简单路径。
回路:若路径的第一个顶点和最后一个顶点相同,则是回路。
简单回路:第一个顶点和最后一个顶点相同,其它各顶点都不重复的回路则是简单回路。
三、图的存储结构
上面了解了"图的基本概念",下面开始介绍图的存储结构。图的存储结构,常用的是"邻接矩阵"和"邻接表"。
3.1 邻接矩阵
邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。假设图中顶点数为n,则邻接矩阵定义为:

下面通过示意图来进行解释。
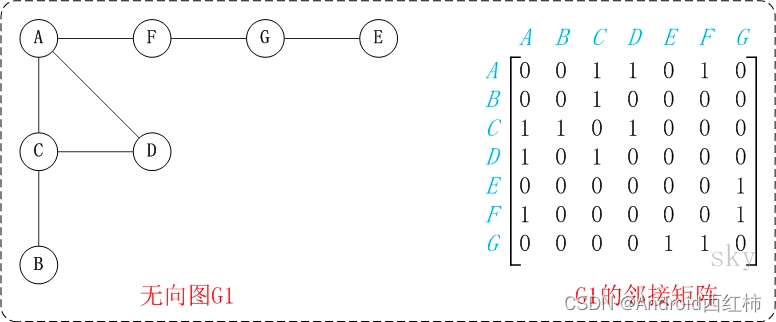
图中的G1是无向图和它对应的邻接矩阵。
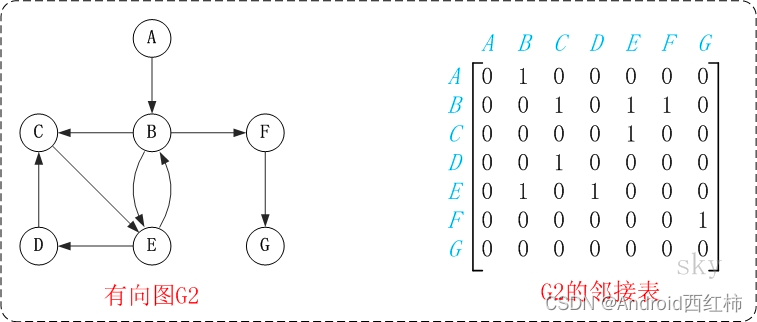
图中的G2是有向图和它对应的邻接矩阵。
通常采用两个数组来实现邻接矩阵:一个一维数组用来保存顶点信息,一个二维数组来用保存边的信息。
邻接矩阵的缺点就是比较耗费空间。
3.2 邻接表
邻接表是图的一种链式存储表示方法。它是改进后的"邻接矩阵",它的缺点是不方便判断两个顶点之间是否有边,但是相对邻接矩阵来说更省空间。

图中的G1是无向图和它对应的邻接矩阵。
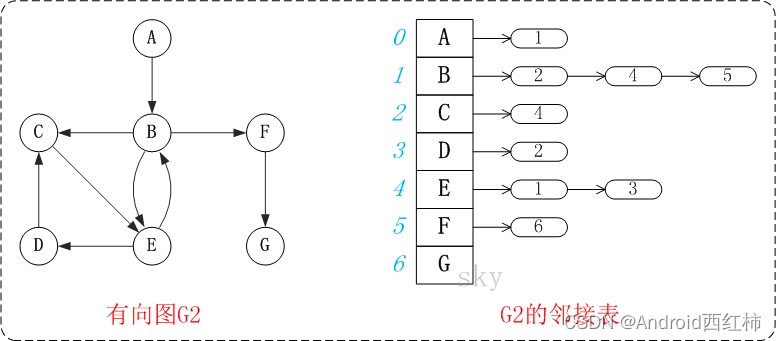
图中的G2是无向图和它对应的邻接矩阵。
3.3 十字链表
对于邻接表来说,计算顶点的入度是不方便的,那么有没有一种存储方式能够轻松的计算顶点的入度和出度呢,在十字链表中重新定义了节点的结构:
3.4 使用
实际使用,我们在拓扑排序中,使用邻接矩阵来实现,这是i个二维数组
首先,定义一些属性,用来存放节点数、顶点名称、排序后的顺序,图关系矩阵
/*** 节点个数*/public int size;/*** 顶点名称*/char [] nodeName;/*** 排序后的顺序*/List result;/*** 图关系矩阵*/int [][] matrix;
然后排序
// 排序public void tuopuSort() {System.out.println("\n");// 一个一维数组,用来保存顶点的入度int indegree[] = new int[size];boolean indegreeV[] = new boolean[size];// 给入度输入值for(int i = 0; i < size; i ++) {indegreeV[i] = false;for (int j = 0; j < size; j ++) {if (matrix[i][j] == 1) {indegree[j] = indegree[j] + 1;}}}System.out.println("\n");//开始进行遍历LinkedList<String> nodes = new LinkedList<String>();// 将入度为 0 的节点入队列for (int x = 0; x < size; x ++) {if (indegree[x] == 0) {System.out.println(nodeName[x]);nodes.add(String.valueOf(nodeName[x]));}}int j = 0;while (!nodes.isEmpty()) {for (int x = 0; x < size; x ++) {System.out.println("\n 数组 x = " + x + ", ");if (indegree[x] == 0 && !indegreeV[x]) {indegreeV[x] = true;String s = nodes.poll();System.out.println("add = " +s);result.add(s);// 找到跟它相关的节点,,入度 -1for (int y = 0; y < size; y ++) {if (matrix[x][y] == 1) {System.out.println("相关的节点 -1 = " + y);indegree[y] = indegree[y] - 1;if (indegree[y] == 0) {System.out.println("相关的节点 -1 后, 入度为0, " + nodeName[y]);nodes.add(String.valueOf(nodeName[y]));}}}} else {}}j ++;}System.out.println(result);}
四、图的遍历
深度优先遍历(DFS) & 广度优先遍历(BFS)
详细请看另外一篇文章
相关文章:

【基础知识整理】图的基本概念 邻接矩阵 邻接表
一、图概述 定义: 图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的; 其中,点通常被成为"顶点(vertex)“,而点与点之间的连线则被成为"边或弧”(edege)。 通常记为,G(V,E)。 图是一种重要的…...

5.程序控制结构|Java学习笔记
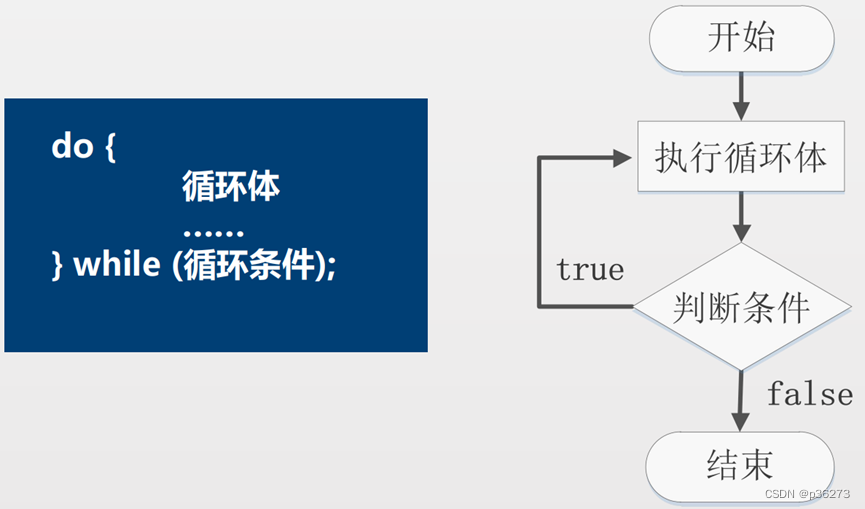
文章目录 程序流程控制介绍顺序控制分支控制分支控制if elseswitch分支结构 循环控制for循环控制while循环控制do...while循环控制跳转控制语句breakcontinuereturn 程序流程控制介绍 顺序控制分支控制循环控制 顺序控制 程序从上到下逐行地执行,中间没有任何判断…...
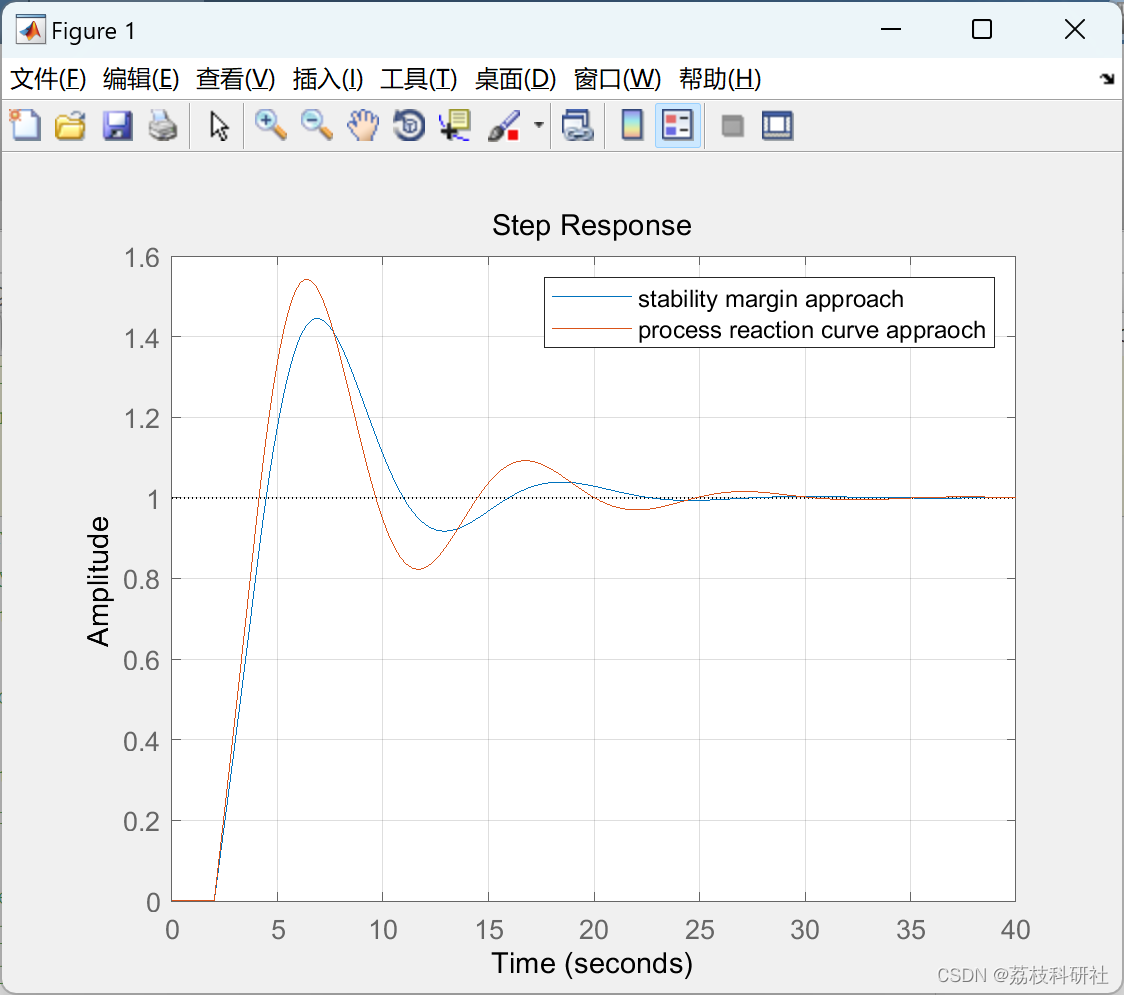
【最优PID 整定】PID性能指标(ISE,IAE,ITSE和ITAE)优化、稳定性裕量(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
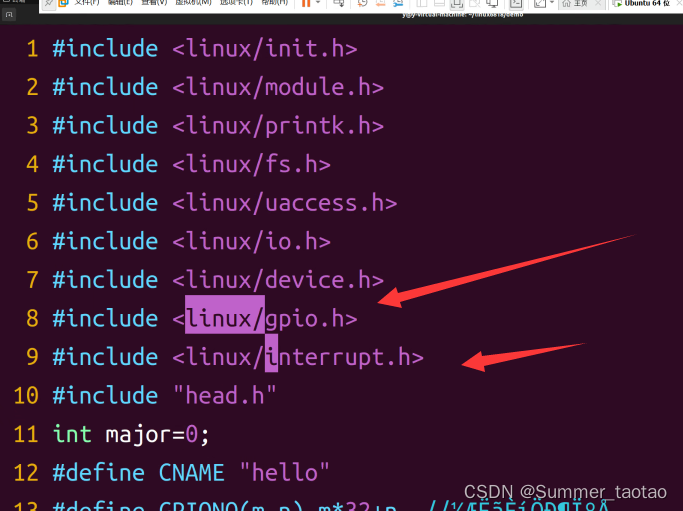
Linux内核中断和Linux内核定时器
目录 Linux内核中断 Linux内核定时器 Linux内核中断 int request_irq(unsigned int irq, irq_handler_t handler, unsigned long flags,const char *name, void *dev) 功能:注册中断 参数: irq : 软中断号 gpio的软中断号 软中断号 gpio_to_i…...

OMG--IDL(Interface Definition Language)
OMG--IDL(Interface Definition Language) 1 概述2 内容缩写IDL 语法和语义概述词法约定ISO Latin-1的字母字符如下表十进制数字字符图形字符格式化字符Tokens注释标识符冲突规则转义标识符关键字IDL识别的其他字符字面量 预处理IDL 语法构建块核心数据类…...

英语学习:M开头
machine 机器 mad 发疯的,生气的 madam 女士,夫人 madame 夫人 magazine 杂志 magic 有魔力的 maid 女仆,侍女 mail 邮递 mailbox 邮箱 mainland 大陆 major 较大的,主要的 majority 大多数 male 雄的 man 人类 man…...
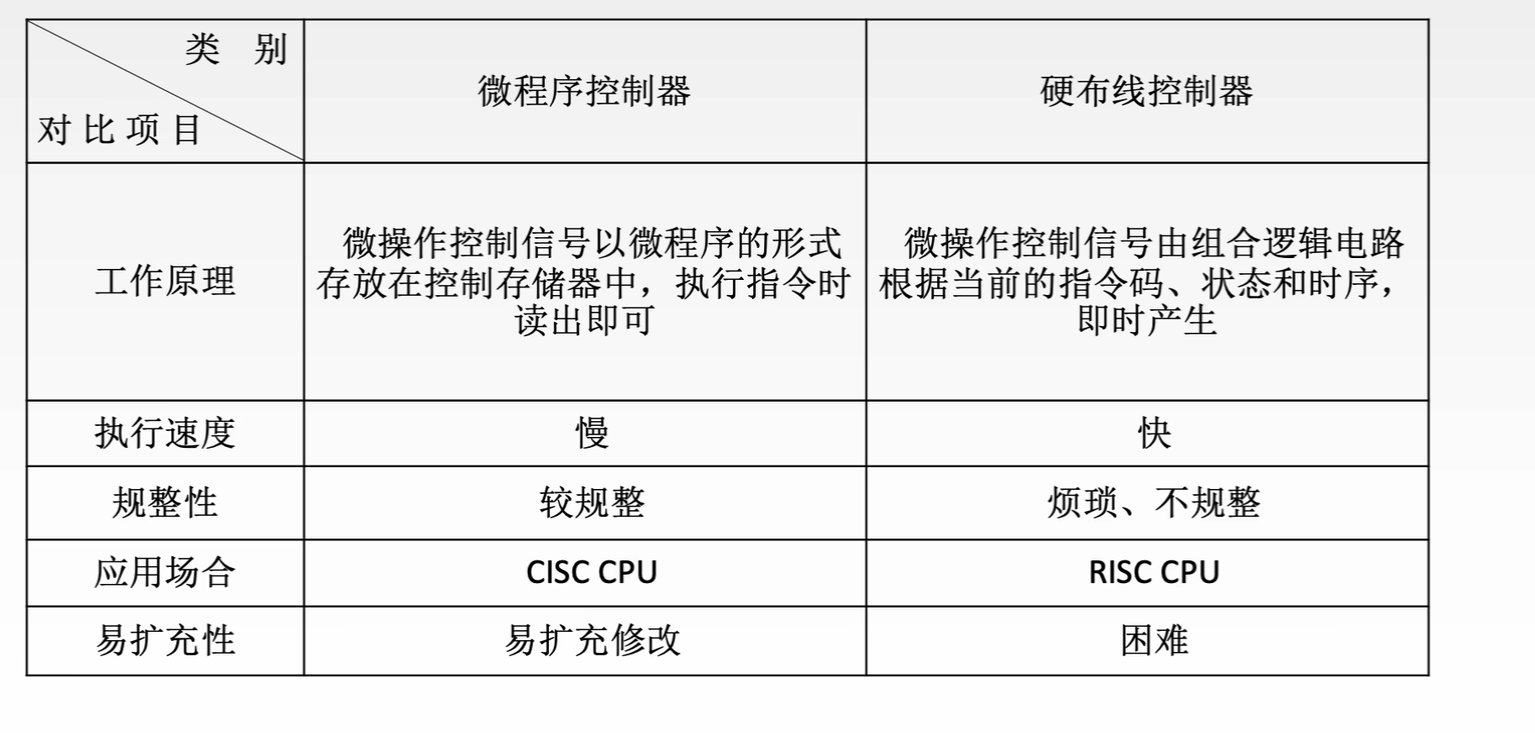
【计算机组成原理与体系结构】控制器
目录 一、CPU的功能与基本结构 二、指令周期的数据流 三、数据通路 四、硬布线控制器 五、微程序控制器 六、微指令 一、CPU的功能与基本结构 运算器基本结构 控制器基本结构 CPU的基本结构 二、指令周期的数据流 取址周期 间址周期 中断周期 指令周期流程 三、数据通路 …...

结构化命令
章节目录: 一、使用 if-then 语句二、if-then-else 语句三、嵌套 if 语句四、test 命令4.1 数值比较4.2 字符串比较4.3 文件比较 五、复合条件测试六、if-then 的高级特性6.1 使用单括号6.2 使用双括号6.3 使用双方括号 七、case 命令八、结束语 本章内容࿱…...
Java Web实训项目:西蒙购物网
文章目录 一、创建数据库和表1、创建数据库2、创建用户表3、创建类别表4、创建商品表5、创建订单表 二、创建Simonshop项目1、创建web项目2、修改Artifacts名称:simonshop3、重新部署项目4、编辑首页5、启动应用,查看效果 三、创建实体类1、用户实体类2、…...

ChatGPT Prompt 提示词设计技巧必知必会
本文内容整理自图灵社区直播《朱立成:ChatGPT Prompt提示词技巧必知必会》。 朱立成,图灵社区《ChatGPT即学即用》视频课程作者,软件工程师,对新事物充满好奇,关注ChatGPT应用。2001年毕业于浙江大学,从事软…...
尚硅谷-云尚办公-项目复盘
尚硅谷-云尚办公-项目复盘 资料地址本文介绍问题汇总问题1.knife4j无法下载 视频4问题2.dev等含义 视频5问题3.wrapper继承/实现图 视频8问题4.修改统一返回结果 视频11问题5.修改后新增也变修改 视频29问题6.redis中key值乱码 视频55-60问题7.RangeError: Maximum call stack …...
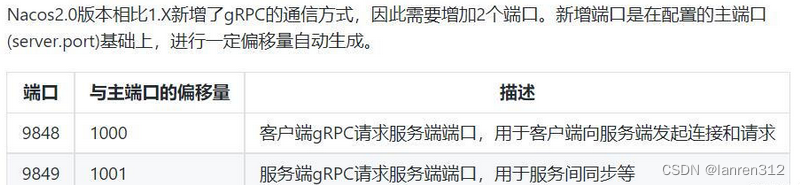
nacos升级到2.0.3(单机模式)
前提:https://github.com/alibaba/spring-cloud-alibaba/wiki/版本说明 Spring Cloud AlibabaSpring CloudSpring BootNacos2.2.7.RELEASESpring Cloud Hoxton.SR122.3.12.RELEASE2.0.3 一、pom.xml文件 <parent><groupId>org.springframework.boot&…...
Koa学习3:用户添加、错误处理
模型 在src目录下创建model目录,用来存放模型 创建用户模型 user.model.js 注意: UUID类型是无法自增的,将id设置为UUID类型时只需要为其指定默认值即可 // 数据类型 const { DataTypes } require(sequelize); // 导入已经连接了数据库…...
网络安全入门学习第十五课——PHP基础
文章目录 一、WEB技术1、什么是web2、B/S架构3、C/S架构 二、PHP概述1、PHP是什么2、PHP受欢迎的原因3、基于MVC模式的PHP框架4、常用编译工具5、PHP环境搭建6、开发工具 三、PHP基本语法格式1、标记2、输出语句3、注释4、标识符 四、数据与运算1、常量1.1、常量定义1.2、预定义…...
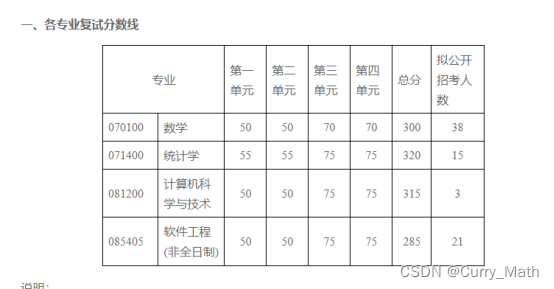
电子科技大学 数学专业-功不唐捐,玉汝于成
电子科技大学 数学专业 功不唐捐,玉汝于成 1.本科背景 本科是坐落于湖南湘潭的湖南科技大学,专业为网络工程专业,因热爱数学专业,所以决定跨考数学专业。 本科专业课平均成绩85,排名10/104。CET 4 474分,…...

Android10.0 iptables用IOemNetd实现删除子链功能的实现
1.前言 在10.0的系统rom定制化开发中,在system中netd网络这块的产品需要中,会要求设置屏蔽ip地址之内的功能, liunx中iptables命令也是比较重要的,接下来就来在IOemNetd这块实现删除创建子链的相关功能 2. iptables用IOemNetd实现删除创建子链功能的实现的核心类 syste…...

OpenGL光照之光照贴图
文章目录 漫反射贴图镜面光贴图放射光贴图代码 每个物体都拥有自己独特的材质从而对光照做出不同的反应的方法。这样子能够很容易在一个光照的场景中给每个物体一个独特的外观,但是这仍不能对一个物体的视觉输出提供足够多的灵活性。 我们将整个物体的材质定义为一个…...

2018~2019 学年第二学期《信息安全》考试试题(B 卷)
北京信息科技大学 2018 ~2019 学年第 2 学期 《信息安全》课程期末考试试卷 B 课程所在学院:计算机学院 适用专业班级:计科 1601-06,重修 考试形式:(闭卷) 一. 选择题(本题满分 10 分,共含 10 道小题,每小题 1 分) 网络中存在的安全漏洞主…...

LeetCode-C#-0002.两数相加
0.声明 该题目来源于LeetCode 如有侵权,立马删除。 解法不唯一,如有新解法可一同讨论。 1.题目 0002两数相加 给你两个非空的链表,表示两个非负的整数,它们每位数字都是按照逆序的方式存储的,并且每个节点只能存储一…...
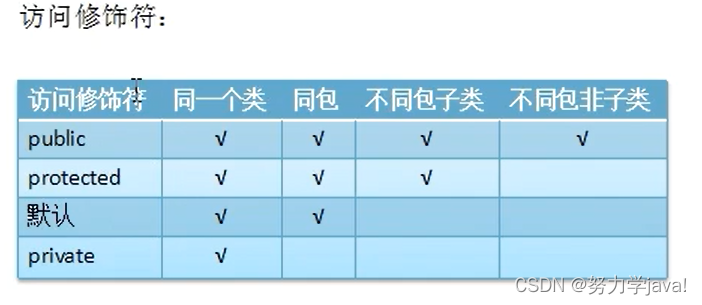
访问修饰符private,default,protected,public访问等级区别
private:private是最严格的访问修饰符,它将成员声明为私有的。私有成员只能在声明它们的类内部访问,其他类无法直接访问私有成员。这样可以确保数据的封装性和安全性。 default(默认):如果没有明确指定访问…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
