华为OD机试真题 JavaScript 实现【找终点】【2023 B卷 100分】,附详细解题思路

一、题目描述
给定一个正整数数组,设为nums,最大为100个成员,求从第一个成员开始,正好走到数组最后一个成员,所使用的最少步骤数。
要求:
- 第一步必须从第一元素开始,且1 <= 第一步的步长 < len/2,len为数组的长度,需要自行解析;
- 第二步开始,只能以所在成员的数字走相应的步数,不能多也不能少,如果目标不可达返回-1,只输出最少的步骤数量;
- 只能向数组的尾部走,不能往回走;
二、输入描述
由正整数组成的数组,以空格分隔,数组长度小于100,请自行解析数据数量。
三、输出描述
正整数,表示最少的步数,如果不存在输出-1。
四、解题思路
- 给定一个正整数数组,设为nums;
- 遍历nums,根据题目描述“第一步的步长 < len/2”,因为从0开始,所以循环到nums.length / 2 - 1;
- 根据当前index的值,再走n步,循环往复;
- 比如测试的输入
4 2 9 5 3 8 1 5 5 7 2 6 9; - 第一步为数字4,前进4步,到达nums[4],即为3;
- 再走3步,到达nums[7],即为5;
- 再走5步,正好到达最后一个数字9,完美;
- 比如测试的输入
- 判断最后一次的下角标是否等于最后一个,如果等于,则符合要求;
- 取符合要求的最小步骤数;
- 输出使用的最少步骤数,如果没有,输出-1。
五、JavaScript算法源码
/*** 求从第一个成员开始,正好走到数组最后一个成员,所使用的最少步骤数。*/
function calculate(nums) {const len = nums.length;// 最少步骤数,最大为100个成员let minSteps = Infinity;// 第一步的步长 < len/2for (let i = 0; i < Math.floor(len / 2); i++) {let index = i;let stepCount = 1;// 比如第一步为数字4,前进4步,到达nums[4],即为3,再走3步,到达nums[7],即为5,再走5步,正好到达最后一个数字9while (index < len - 1) {index += nums[index];stepCount++;}// 判断最后一次的下角标是否等于最后一个,如果等于,则符合要求if (index === len - 1) {minSteps = Math.min(minSteps, stepCount);}}// 输出使用的最少步骤数,如果没有,输出-1return minSteps === Infinity ? -1 : minSteps;
}
六、效果展示
1、输入
4 2 9 5 3 8 1 5 5 2 2 1 9
2、输出
3
3、说明
比如走0步,值为4,前进4步,到达nums[4],即为3,再走3步,到达nums[7],即为5,再走5步,正好到达最后一个数字9,花费4步。
比如走1步,值为2,前进2步,到达nums[9],即为1,再走1步,正好到达最后一个数字9,花费3步。
比如走3步,值为5,前进5步,到达nums[8],即为5,再走5步,正好到达最后一个数字9,花费3步。
取符合要求的最小步数,所以输出3。

🏆下一篇:华为OD机试真题 JavaScript 实现【相对开音节】【2022Q4 100分】,附详细解题思路
🏆本文收录于,华为OD机试(JavaScript)真题(A卷+B卷)
每一题都有详细的答题思路、详细的代码注释、样例测试,订阅后,专栏内的文章都可看,可加入华为OD刷题群(私信即可),发现新题目,随时更新,全天CSDN在线答疑。

相关文章:

华为OD机试真题 JavaScript 实现【找终点】【2023 B卷 100分】,附详细解题思路
一、题目描述 给定一个正整数数组,设为nums,最大为100个成员,求从第一个成员开始,正好走到数组最后一个成员,所使用的最少步骤数。 要求: 第一步必须从第一元素开始,且1 < 第一步的步长 &…...

详解数据仓库数据湖及湖仓一体
比别人更快接收好文章 随着近几年数据湖概念的兴起,业界对于数据仓库和数据湖的对比甚至争论就一直不断。有人说数据湖是下一代大数据平台,各大云厂商也在纷纷的提出自己的数据湖解决方案,一些云数仓产品也增加了和数据湖联动的特性。 但是…...
)
基于注解切换、Hikari实现的SpringBoot动态数据源(支持JNDI)
实现效果 先说效果,要实现方法级别注解切换当前数据源,不设置注解时走默认数据源,同时支持JNDI源。 总体思路 Spring框架中存在一个抽象类AbstractRoutingDataSource,他是一个可以动态选择当前DataSource的路由类,我…...
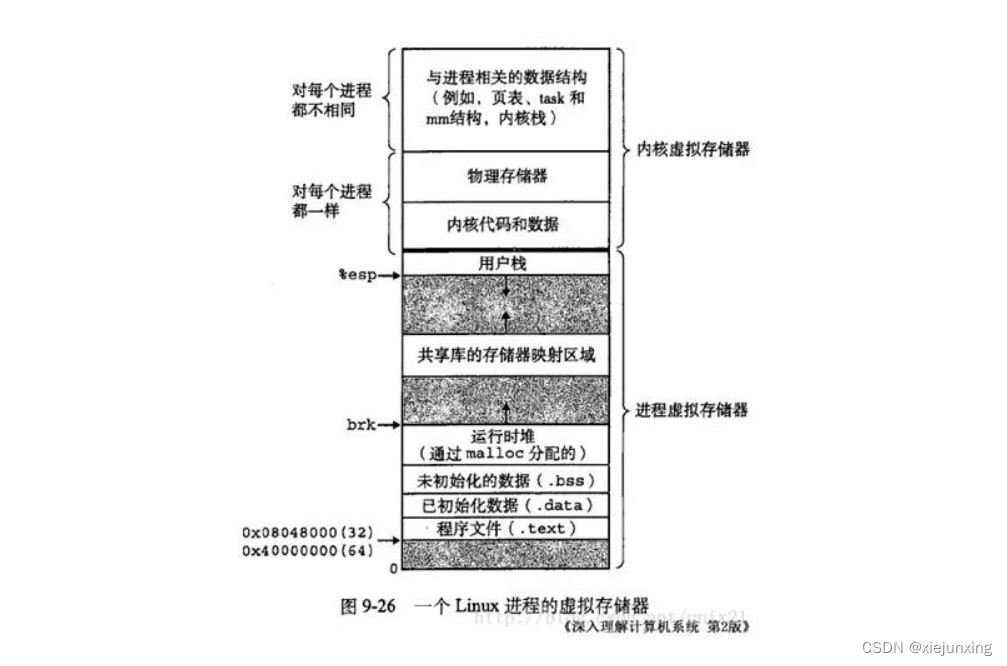
Java中的动态链接VS操作系统动态链接
在操作系统OS中为了优化内存的使用会采用一种动态链接方式,一个文件想要在操作系统中运行必须经过编译、汇编译、链接、装载等步骤。可以参考Java程序是怎么跑起来的。本篇主要讲解Java栈帧中动态链接部分与操作系统的的动态链接的区别与联系 操纵系统为什么需要动态…...

深入理解Linux虚拟内存管理(七)
系列文章目录 Linux 内核设计与实现 深入理解 Linux 内核 Linux 设备驱动程序 Linux设备驱动开发详解 深入理解Linux虚拟内存管理(一) 深入理解Linux虚拟内存管理(二) 深入理解Linux虚拟内存管理(三) 深入理…...

GSR II 智能速度辅助系统的型式认证和系统作为独立技术单元的型式认证测试流程和技术要求
智能速度辅助系统ISA的型式认证和系统作为独立技术单元的型式认证测试流程和技术要求 补充欧洲议会和欧洲理事会第2019/2144号条例,为机动车智能速度辅助系统的型式认证和这些系统作为独立技术单元的型式认证规定了详细的测试程序和技术要求,并修订该条例的附件二 (1)(EU…...
工厂方法模式(五)
过气的,终究是过气了 上一章简单介绍了工厂模式(四), 如果没有看过,请观看上一章 一.工厂方法模式 工厂方法模式,通过定义工厂父类负责定义创建对象的公共接口,而子类则负责生成具体的对象。 将类的实例化(具体产品的创建&…...

力扣笔记(每日随机一题)——最佳买卖股票时机含冷冻期
问题(中等) 给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票): 卖出股票后&a…...
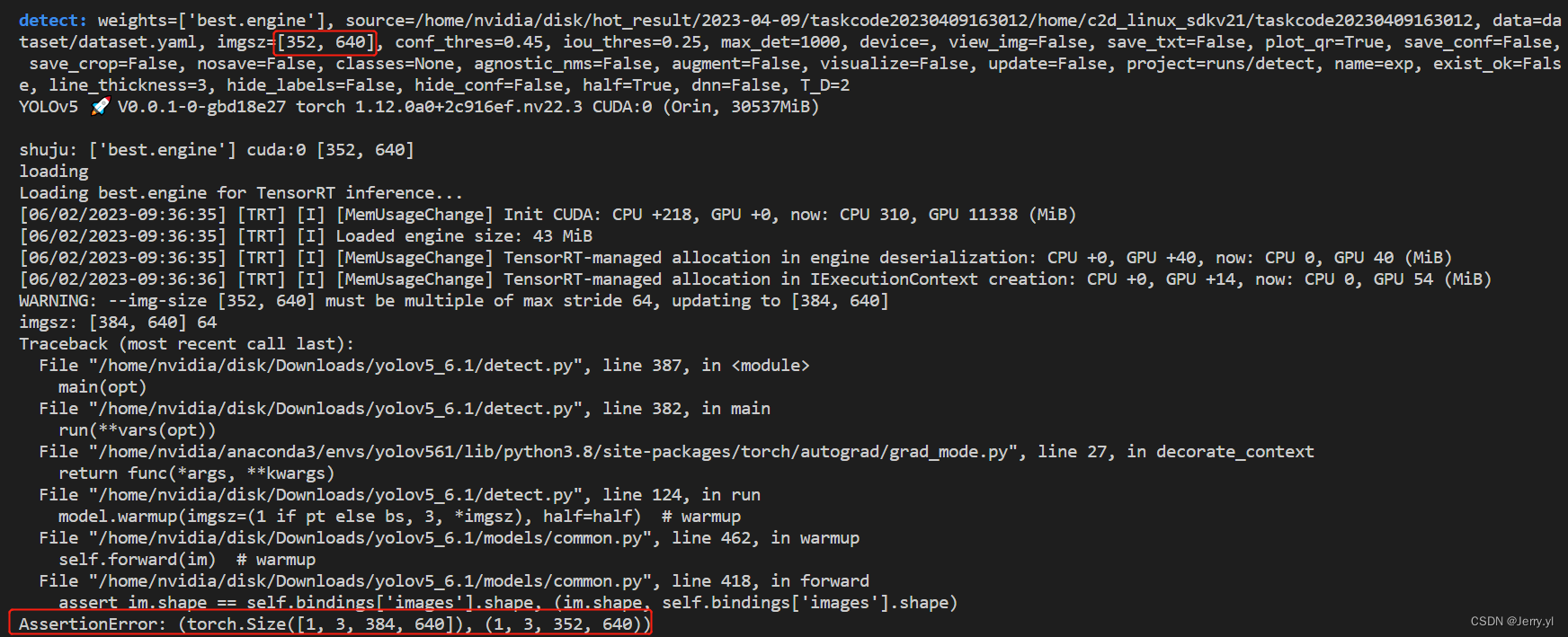
yolov5 6.1 关于 tensorrt 加速的使用以及问题说明
文章目录 1. 参考连接2. 使用说明2.1 导出加速模型2.1 使用加速模型2.2 加速参数对比 3. 问题说明3.1 在 Tensorrt 8.4.1.5 版本上使用 export.py 导出失败的问题3.2 把模型文件由 best.pt 更换成加速后的 best.engine 后,执行推理时标注的类别名不正确的问题3.3 导…...
用法介绍)
SVR(支持向量机)用法介绍
一、SVR回归介绍 SVR(Support Vector Regression)是支持向量机(SVM)在回归问题中的应用。与SVM分类模型相似,SVR也是一种非概率性算法,通过使用核函数将数据映射到高维空间,并在该空间上寻找最优的超平面与训练数据之间的间隔最大化…...

是面试官放水,还是公司实在是太缺人?这都没挂,腾讯原来这么容易进···
本人211非科班,之前在字节和腾讯实习过,这次其实没抱着什么特别大的希望投递,没想到腾讯可以再给我一次机会,还是挺开心的。 本来以为有个机会就不错啦!没想到能成功上岸,在这里要特别感谢帮我内推的同学&…...
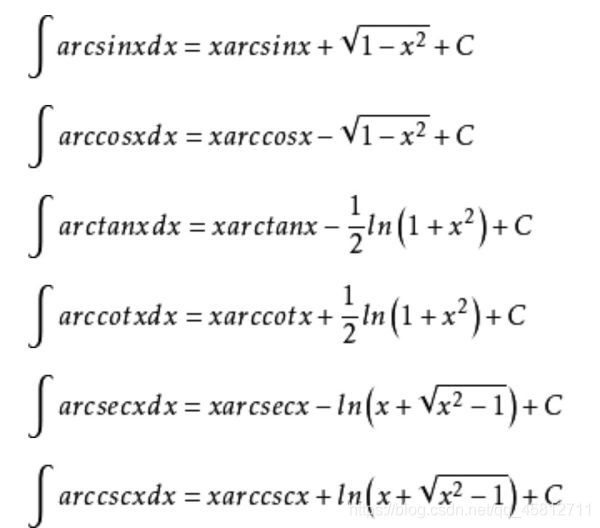
算法模板(5):数学(1):数学知识(1)
数论 整数的整除性 [x]表示不超过x的最大整数,叫做取整函数或高斯函数。设整数a,b不同时为零,则存在一对整数m,n,使得 ( a , b ) a m b n (a, b) am bn (a,b)ambn。注:a和b的最大公因数会写成 (a, b)…...
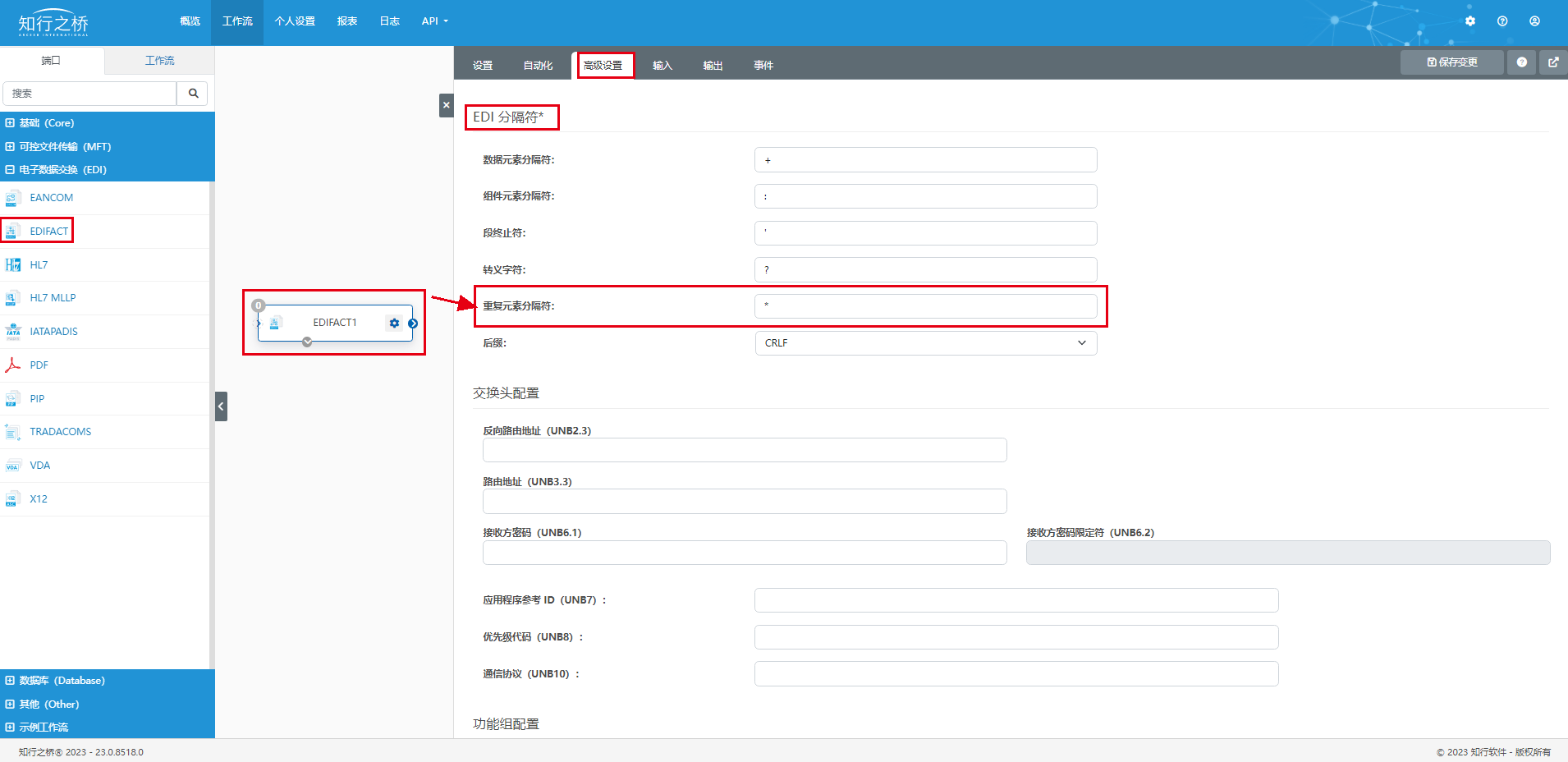
电子行业 K 公司对接 Nexperia EDI 项目案例
项目背景 Nexperia 是一家全球领先的半导体制造商,专注于提供高性能、高可靠性和创新性的半导体解决方案。公司成立于2017年,是前飞思卡尔半导体业务的一部分,并在全球范围内拥有多个设计、研发和生产基地。 Nexperia 使用 EDI(…...

chatgpt赋能python:Python如何将英文转化为中文的最佳方法
Python如何将英文转化为中文的最佳方法 介绍 在现代全球化社会中,国与国之间的交流越来越频繁,相应的语言翻译工具的需求也愈发迫切。Python是一种易于学习、快速上手的编程语言,适合初学者和经验丰富的程序员使用,在语言翻译方…...
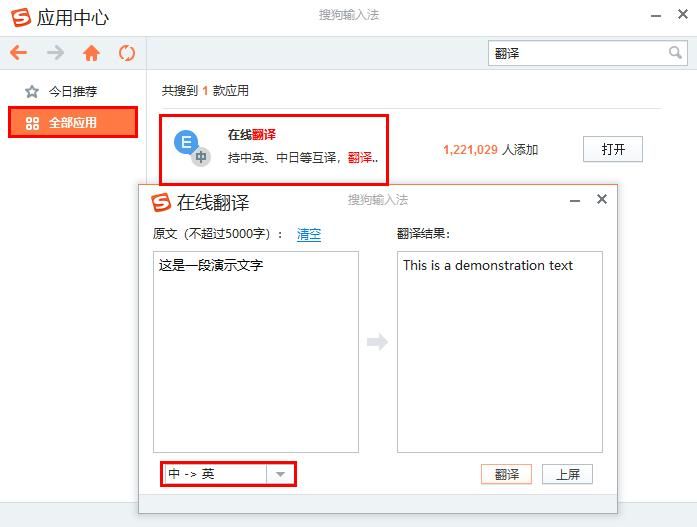
知道这些英文文档翻译的方式吗
在工作中,大家有没有遇到领导交给你一份外语的文档,要你去观看和理解,但是我们看不太懂或者没啥时间去一点点翻译怎么办呢?我们就需要有工具来将文档翻译,它是一项非常实用和便捷的功能,它可以将文档中的文…...
供应链安全
供应链安全 目录 文章目录 供应链安全目录本节实战可信任软件供应链概述构建镜像Dockerfile文件优化镜像漏洞扫描工具:Trivy检查YAML文件安全配置:kubesec准入控制器: Admission Webhook准入控制器: ImagePolicyWebhook关于我最后…...

华硕天选4原装Windows11系统带ASUSRECOVERY恢复工厂模式安装
华硕工厂恢复系统 ,安装结束后带隐藏分区以及机器所有驱动软件,奥创Myasus Recovery 文件地址https://pan.baidu.com/s/1Pq09oDzmFI6hXVdf8Vqjqw?pwd3fs8 提取码:3fs8 文件格式:5个底包(HDI KIT COM MCAFEE EDN) 1个引导工具TLK 支持ASUSRECOVERY型…...
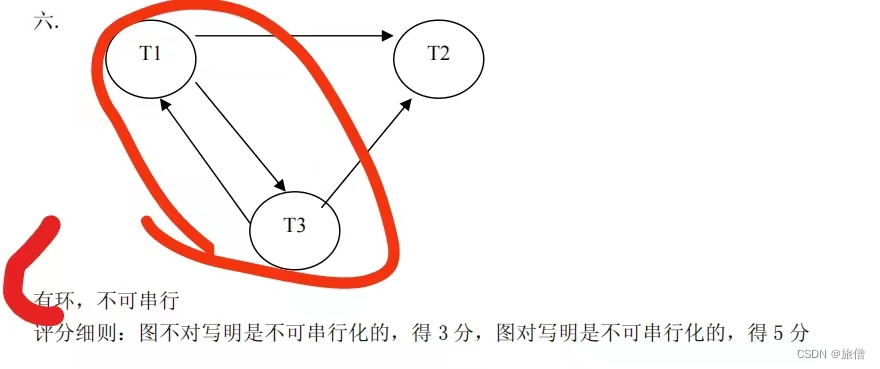
数据库期末复习(8)并发控制
笔记 数据库DBMS并发控制(1)_旅僧的博客-CSDN博客 数据库 并发控制(2)死锁和意向锁_旅僧的博客-CSDN博客 同一个对象不能既有slock又有xlock; 冲突可串行化和锁 怎么判断是否可以进行冲突可串行化:简便的方法是优先图 只有不同对象和同一对象都是读才不能发生非串行化调…...
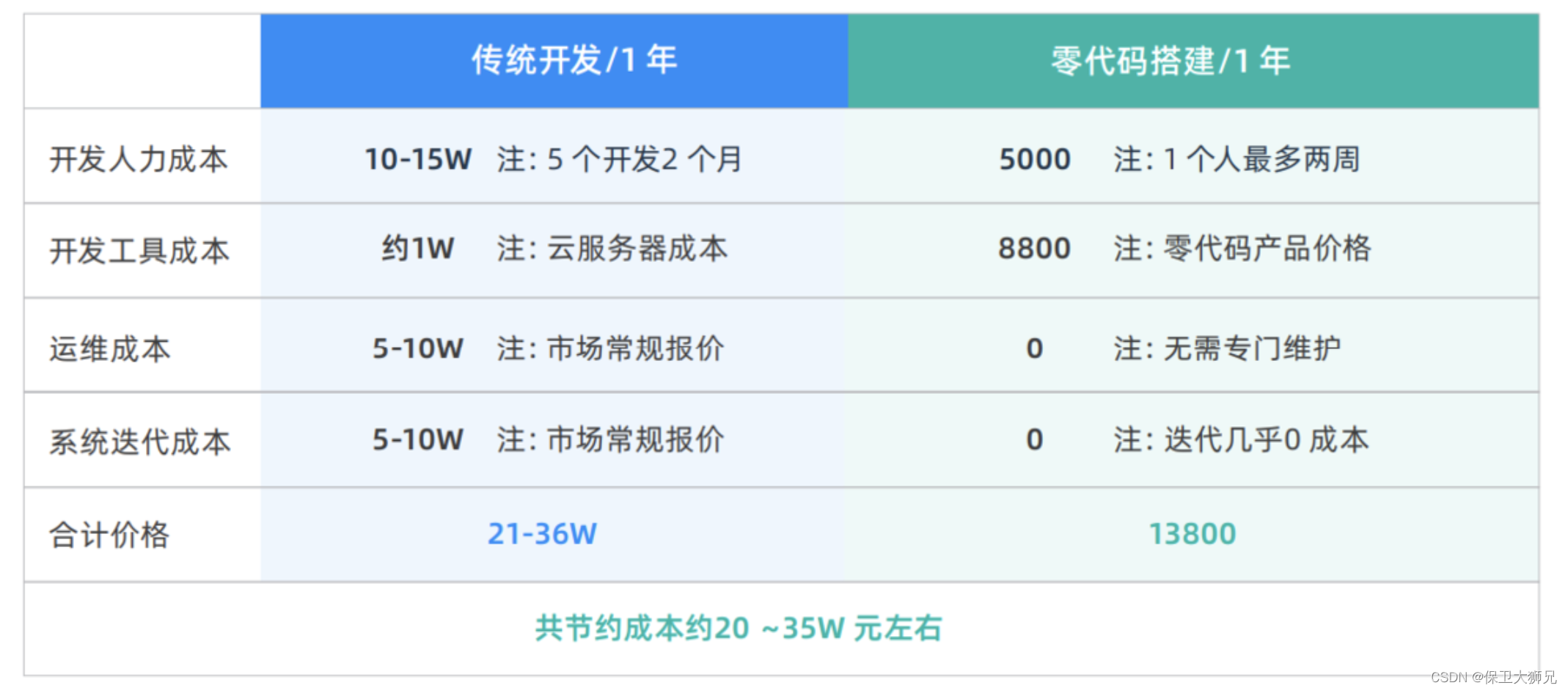
一文说透:低代码开发平台和零代码平台区别是什么?
低代码开发平台和零代码平台区别是什么? 一个简单的例子就可以解释清楚。 假设你想入住一套新房,回看住房变迁史: 最原始方式是:自己建造往后一点,交付“毛坯房”:开发商统一建小区,不需要自…...

4.将图神经网络应用于大规模图数据(Cluster-GCN)
到目前为止,我们已经为节点分类任务单独以全批方式训练了图神经网络。特别是,这意味着每个节点的隐藏表示都是并行计算的,并且可以在下一层中重复使用。 然而,一旦我们想在更大的图上操作,由于内存消耗爆炸,…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
