Mysql数据库的时间(3)一如何用函数插入时间
暂时用下面四个日期函数插入时间
如:insert into Stu(time) values (now());
| Mysql的时间函数 | 描述 | 对应的Mysql的时间类型 |
|---|---|---|
| now()/sysdate() | NOW()函数以`'YYYY-MM-DD HH:MM:SS'返回当前的日期时间 | date/time/dateTime/timeStamp/year |
| curDate()/current_date() | 返回当前的日期YYYY-MM-DD | date/year |
| curTime()/current_time() | 返回当前的时间HH:MM:SS | time |
日期函数
now()/curtime()/curdate()
这些函数的值是会随着时区的不同而获得到不同的值的.
1、now()/sysdate()返回当前日期和时间
NOW()函数和sysdate()都是以`'YYYY-MM-DD HH:MM:SS'返回当前的日期时间,可以直接存到DATETIME字段中。
select now(); select sysdate();
返回2023-02-16 11:26:05 和 2023-02-16 11:26:05
2、date()从日期或日期时间表达式中提取日期值
SELECT DATE("2017-06-15 11:11:16");
---- 返回2017-06-15
3、year(d)返回日期值 d 的年
select YEAR("2023:02:16");
--返回20234、monte(d)返回日期值 d 的月
select MONTH("2023:02:16");
--- 返回 25、day(d)返回日期值 d 的天
SELECT DAY("2017-06-15");
---- 返回15
6、curDate()/current_date()返回当前日期
SELECT CURDATE();
SELECT CURRENT_DATE();
---- 返回2019-02-19
7、current_time()/curTime()返回当前时间
SELECT CURRENT_TIME();
---- 返回11:40:45
8、current_timeStamp()返回当前日期和时间
SELECT CURRENT_TIMESTAMP();
---- 返回2019-02-19 11:41:32
9、addDate(d,n)计算起始日期 d 加上 n 天的日期
SELECT ADDDATE("2017-06-15", INTERVAL 10 DAY);
---- 返回2017-06-25
10、addTime(t,n)时间 t 加上 n 秒的时间
SELECT ADDTIME('2011-11-11 11:11:11', 5);
---- 返回2011-11-11 11:11:16
11、dateDiff(d1,d2)计算日期 d1->d2 之间相隔的天数
SELECT DATEDIFF('2001-01-01','2001-02-02');
---- 返回-32
12、date_format按表达式 f的要求显示日期 d
SELECT DATE_FORMAT('2011.11.11 11:11:11','%Y-%m-%d %r');
---- 返回2011-11-11 11:11:11 AM
13、dayName(d)返回日期 d 是星期几,如 Monday,Tuesday
SELECT DAYNAME('2011-11-11 11:11:11');
---- 返回Friday
14、dayOfMonth(d)计算日期 d 是本月的第几天
SELECT DAYOFMONTH('2011-11-11 11:11:11');
---- 返回11
15、dayOfWeek(d)日期 d 今天是星期几,1 星期日,2 星期一,以此类推
SELECT DAYOFWEEK('2011-11-11 11:11:11');
---- 返回6
16、dayOfYear(d)计算日期 d 是本年的第几天
SELECT DAYOFYEAR('2011-11-11 11:11:11');
---- 返回315
17、extract(type FROM d)从日期 d 中获取指定的值,type 指定返回的值
type可取值为:
MICROSECOND
SECOND
MINUTE
HOUR
DAY
WEEK
MONTH
QUARTER
YEAR
SECOND_MICROSECOND
MINUTE_MICROSECOND
MINUTE_SECOND
HOUR_MICROSECOND
HOUR_SECOND
HOUR_MINUTE
DAY_MICROSECOND
DAY_SECOND
DAY_MINUTE
DAY_HOUR
YEAR_MONTH
SELECT EXTRACT(MINUTE FROM '2011-12-13 14:15:16');
---- 返回15
18、unix_TimeStamp()得到时间戳
SELECT UNIX_TIMESTAMP('2019-2-19');
SELECT UNIX_TIMESTAMP(expression);
---- 返回1550505600
19、from_unixtime()时间戳转日期
SELECT FROM_UNIXTIME(1550505600);
---- 返回2019-02-19 00:00:00
SELECT FROM_UNIXTIME(1550505600, '%Y-%m-%d');
---- 返回2019-02-19
相关文章:

Mysql数据库的时间(3)一如何用函数插入时间
暂时用下面四个日期函数插入时间 如:insert into Stu(time) values (now()); Mysql的时间函数描述对应的Mysql的时间类型now()/sysdate()NOW()函数以YYYY-MM-DD HH:MM:SS返回当前的日期时间date/time/dateTime/timeStamp/yearcurDate()/current_date()返回当前的日期YYYY-M…...
)
关于eval函数(将JSON格式的字符串转换成JSON格式对象)
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>关于eval函数</title> </head> <body> <!--JSON是一种行业内的数据交换格式标准。在JS当中以对象的形式存在…...

2023最强软件测试面试题,精选100 道,内附答案版,冲刺金3银4
精挑细选,整理了100道软件测试面试题,都是非常常见的面试题,篇幅较长,所以只放出了题目,答案在评论区! 测试技术面试题 1、什么是兼容性测试?兼容性测试侧重哪些方面? 2、我现在有…...

一文搞懂Docker容器里进程的 pid 是如何申请出来的?
如果大家有过在容器中执行 ps 命令的经验,都会知道在容器中的进程的 pid 一般是比较小的。例如下面我的这个例子。 # ps -ef PID USER TIME COMMAND1 root 0:00 ./demo-ie13 root 0:00 /bin/bash21 root 0:00 ps -ef 不知道大家是否和我一样…...
若依框架如何新增自定义主题风格
若依框架新增主题风格1.实现结果2.实现步骤2.1Settings目录下2.2 variables.scss2.3 sidebar.scss2.4 Logo.vue2.5 Siderbar目录下的index.vue1.实现结果 2.实现步骤 需要改动的文件目录: 2.1Settings目录下 <div class"setting-drawer-block-checbox-it…...
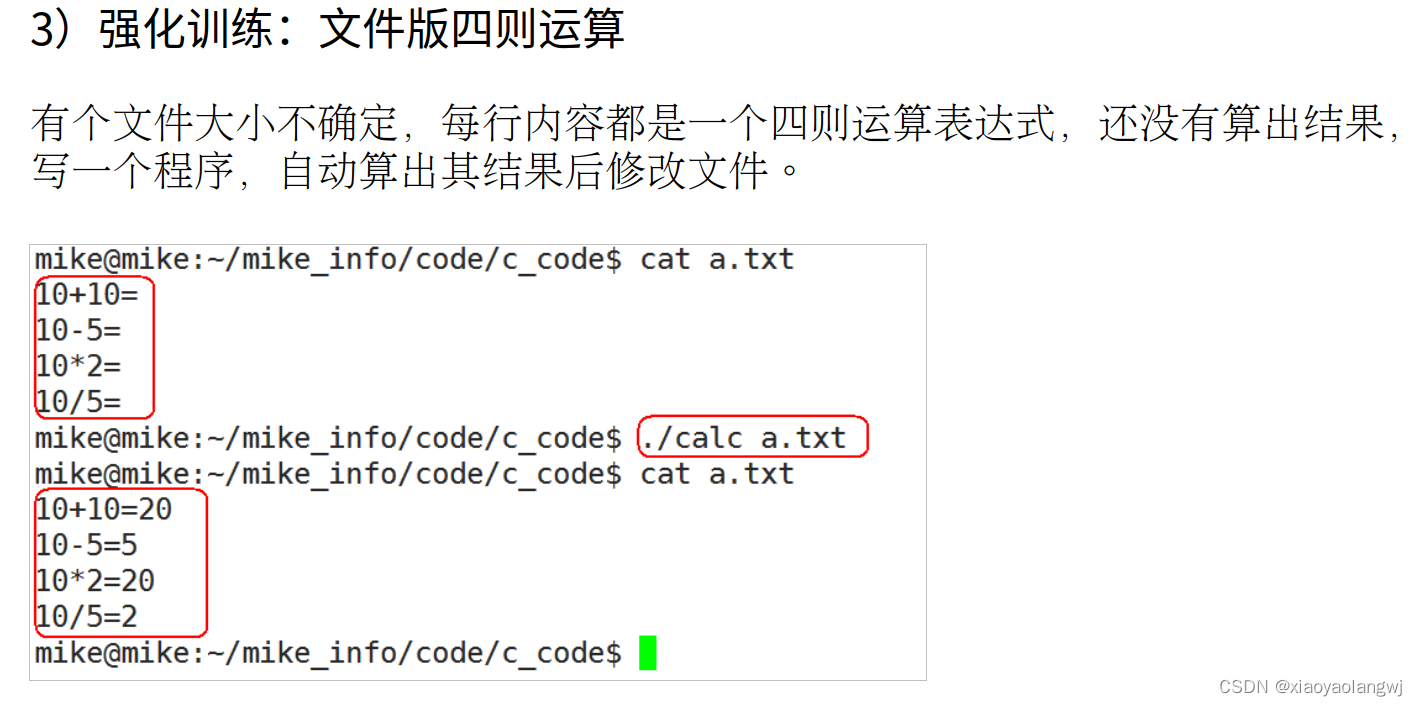
C语言格式化输入和输出; Format格式化
Format格式化 %1s或者%2s,%3s:取字符串的前1,2或者3位。%*c:屏蔽一个字符。%[A-Z]:取一个A到Z的值。 %[^a-z]:不取a到z的值。 %[^\n]:取非换行之前的值。printf("%5d", a):左边补 格式化:有正则在其中。 int main() {printf("%5d\n&quo…...
Revit教程:怎么关掉工具栏的实时提示?
一、Revit中如何关闭工具栏的实时帮助提示 如图1所示,Revit会对每一个命令有一个简单的图文说明,方便不熟悉软件的用户使用。对于已经熟悉软件的用户,会觉得鼠标在菜单上悬停时弹出的实时帮助页面很干扰使用,而且很占内存资源&…...

javascript 简介
JavaScript 是互联网上最流行的脚本语言,这门语言可用于 HTML 和 web,更可广泛用于服务器、PC、笔记本电脑、平板电脑和智能手机等设备。JavaScript 是脚本语言JavaScript 是一种轻量级的编程语言。JavaScript 是可插入 HTML 页面的编程代码。JavaScript…...
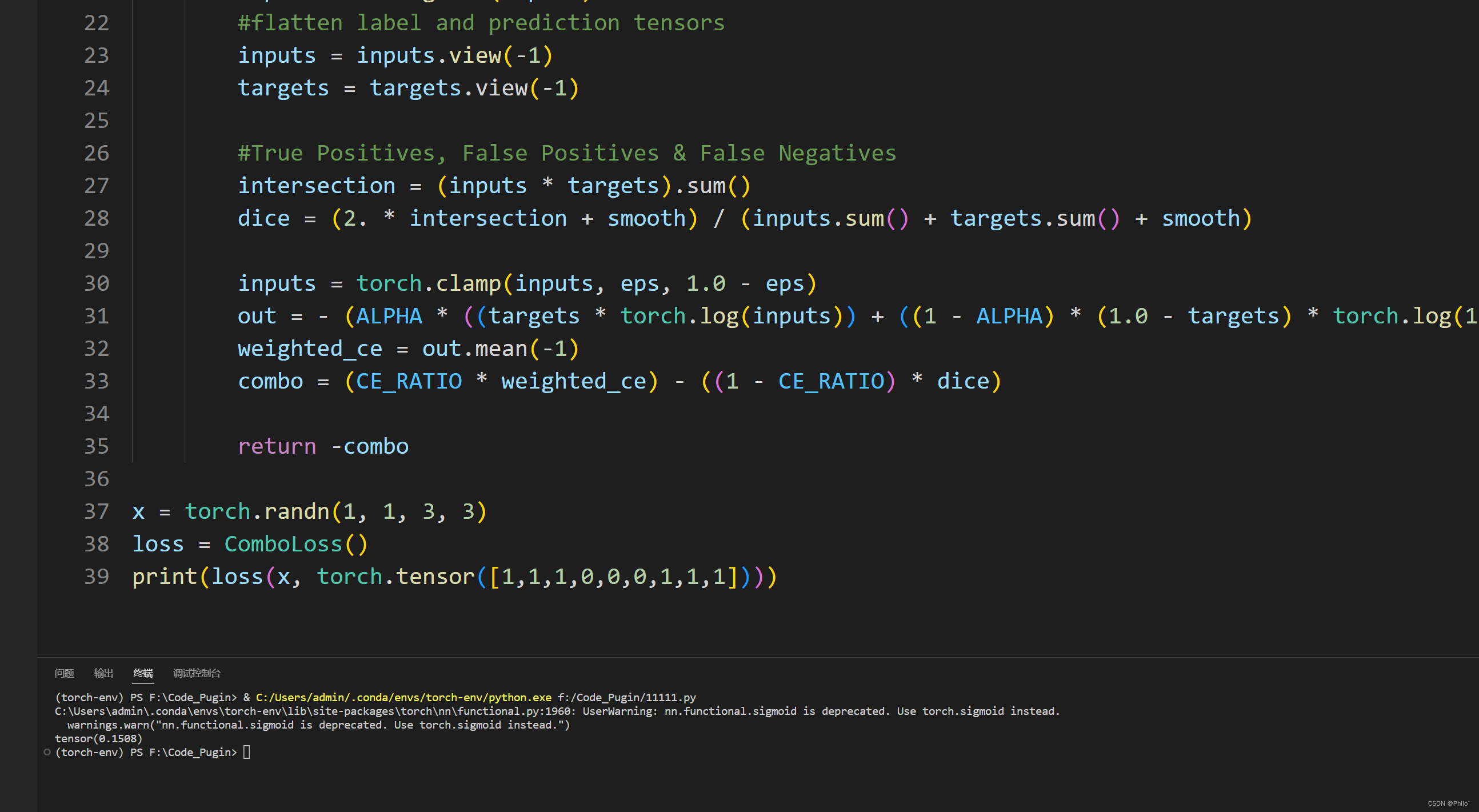
医学图象分割常用损失函数(附Pytorch和Keras代码)
对损失函数没有太大的了解,就是知道它很重要,搜集了一些常用的医学图象分割损失函数,学习一下! 医学图象分割常见损失函数前言1 Dice Loss2 BCE-Dice Loss3 Jaccard/Intersection over Union (IoU) Loss4 Focal Loss5 Tvesky Loss…...
)
【新2023】华为OD机试 - 病菌感染(Python)
华为 OD 清单查看地址:blog.csdn.net/hihell/category_12199275.html 病菌感染 题目 在一个地图中(地图有N*N个区域组成) 有部分区域被感染病菌 感染区域每天都会把周围上下左右的四个区域感染 请根据给定的地图计算多少天以后全部区域都会被感染 如果初始地图上所有区域都…...
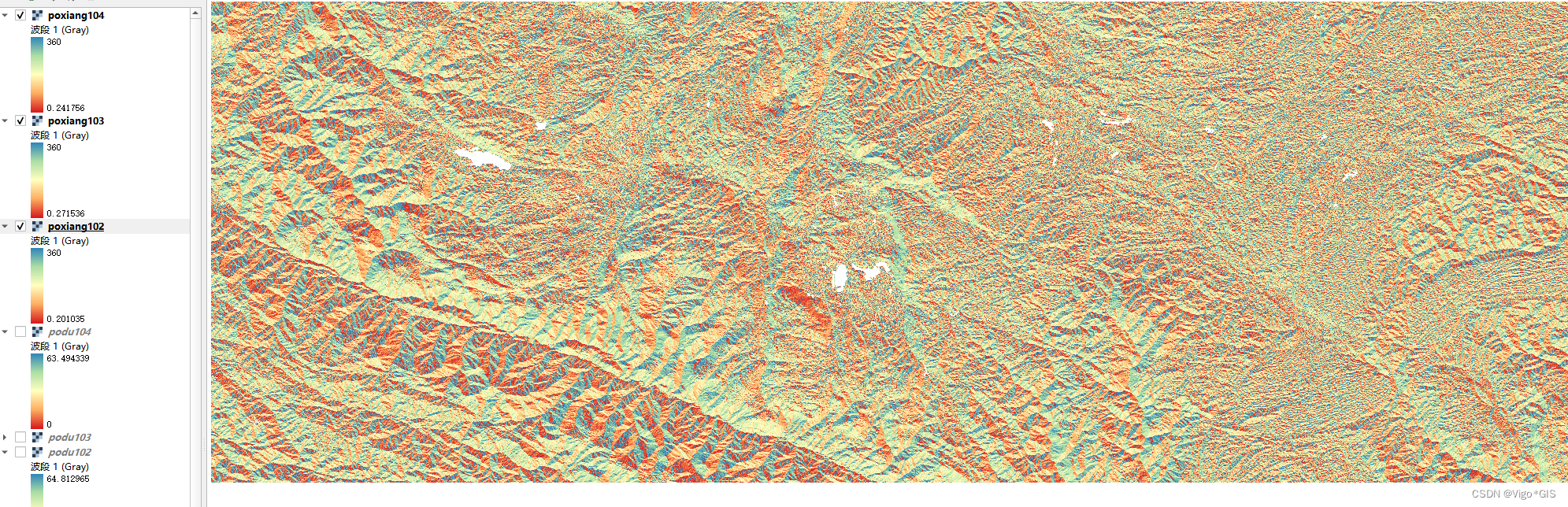
QGIS中进行批量坡向计算
QGIS中进行坡向计算1. 坡向计算中的Z因子(垂直单位与水平单位的比值)2. 坡向计算步骤坡度计算的姊妹篇–坡向计算来了 1. 坡向计算中的Z因子(垂直单位与水平单位的比值) z 因子是一个转换因子,当输入表面的垂直坐标&…...

Redis持久化机制
一、RDB RDB全称Redis Database Backup file(Redis数据备份文件),也被叫做Redis数据快照。 RDB是Redis默认的持久化机制 - RDB持久化文件,速度比较快,而且存储的是一个二进制的文件,传输起来很方便。 - RD…...

2、VUE面试题
1, 如何让CSS只在当前组件中起作用?在组件中的style前面加上scoped2、<keep-alive></keep-alive>的作用是什么?keep-alive 是 Vue 内置的一个组件,可以使被包含的组件保留状态,或避免重新渲染。3, vue组件中如何获取dom元素?使…...

DeepSort:论文翻译
文章目录摘要1、简介2、利用深度关联度量进行排序2.1、轨迹处理和状态估计2.3、匹配的级联2.4、深度外观描述符3、实验4、结论论文链接:https://arxiv.org/pdf/1703.07402.pdf摘要 简单在线实时跟踪(SORT)是一种实用的多目标跟踪方法,专注于简单、有效的…...

Debezium系列之:重置Sqlserver数据库的LSN拉取历史数据
Debezium系列之:重置Sqlserver数据库的LSN拉取历史数据 一、需求背景二、理解LSN三、sqlserver offset数据样式四、写入历史LSN五、观察历史数据六、拉取最新数据一、需求背景 需要重新拉取sqlserver数据库采集表的历史数据或者connector故障,从指定LSN处拉取历史数据二、理解…...
)
一起Talk Android吧(第四百九十四回:在Android中使用MQTT通信四)
文章目录 问题概述解决办法经验总结各位看官们大家好,这一回中咱们说的例子是" 在Android中使用MQTT通信四",本章回内容与前后章节内容无关联。闲话休提,言归正转,让我们一起Talk Android吧! 问题概述 我们在很早之前介绍过MQTT的用法,本章回是在原来的基础上…...
【vcpkg】cpprestsdk之64位编译链接及踩坑
▒ 目录 ▒🛫 问题描述1️⃣ 多版本vs报错指定VS路径2️⃣ error LNK2001: 问题排查通过IDA打开lib文件,确认导出内容查看源码增加参数--editable,重新编译3️⃣ error LNK2001: 外部符号__imp_?close_...去除__imp_🛬 结论vcpkg…...
初始QML
Qt Quick的介绍 : Qt Quick是QML的标准类型和功能库。它包括视觉类型,交互类型,动画,模型和视图,粒子效果和着色器效果。QML 应用程序开发人员可以通过单个导入语句访问所有这些功能,简单来说Qt Quick是一…...

SpringAOP切面实例实现对数据过滤返回,SpringAOP切面实现对用户权限控制,通过@Around注解过滤修改方法返回值
文章目录需求内容:实现:步骤一:导入SpringAOP相关依赖pom.xml步骤二:自定义两个注解步骤三:需要用到的实体类**步骤四:切面具体实现**用法1.需要过滤返回值的方法添加注解FilterByUser2.数据Dto在需要过滤的字段添加Fi…...
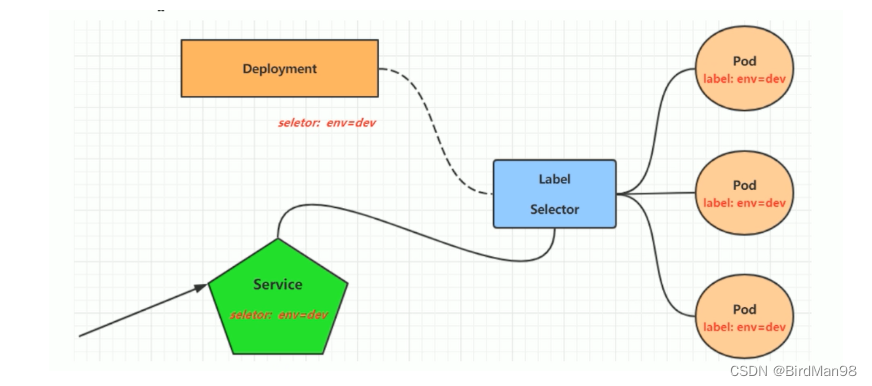
【Kubernetes】【九】Label,Deployment,Service
Label Label是kubernetes系统中的一个重要概念。它的作用就是在资源上添加标识,用来对它们进行区分和选择。 Label的特点: 一个Label会以key/value键值对的形式附加到各种对象上,如Node、Pod、Service等等一个资源对象可以定义任意数量的L…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
