深度学习笔记之Transformer(一)注意力机制基本介绍
深度学习笔记之Transformer——注意力机制基本介绍
引言
从本节开始,将介绍 Transformer \text{Transformer} Transformer模型。本节将介绍注意力机制的基本逻辑。
回顾: Seq2seq \text{Seq2seq} Seq2seq模型中的注意力机制
关于注意力机制 ( Attention ) (\text{Attention}) (Attention),我们并不陌生。在基于循环神经网络的模型结构—— Seq2seq \text{Seq2seq} Seq2seq中介绍了一种注意力机制。
该注意力机制的动机在于:从编码器 ( Encoder ) (\text{Encoder}) (Encoder)中产生的 Context \text{Context} Context向量 C \mathcal C C可能存在梯度消失问题,从而使解码器中生成出的序列信息与编码过程中的初始时刻序列信息关联不大,也就是对齐问题。
而注意力机制在 Seq2seq \text{Seq2seq} Seq2seq结构中的使用逻辑是:使用注意力机制对解码过程中的每一时刻 t = 1 , 2 , ⋯ , T ′ t=1,2,\cdots,\mathcal T' t=1,2,⋯,T′都使用专属于该时刻的 Context \text{Context} Context向量 C t \mathcal C_t Ct来替代原始所有时刻共用的 Context \text{Context} Context向量 C \mathcal C C。关于 C t \mathcal C_t Ct的表示如下:
- 已知解码器 ( Decoder ) (\text{Decoder}) (Decoder)关于 t t t时刻的序列信息 h D ( t ) h_{\mathcal D}^{(t)} hD(t)以及对应编码器 ( Encoder ) (\text{Encoder}) (Encoder)中所有时刻的序列信息 [ h L ; j ; h R ; ( T + 1 − j ) ] ( j = 1 , 2 , ⋯ , T ) \left[h_{\mathcal L;j};h_{\mathcal R;(\mathcal T+1-j)}\right](j=1,2,\cdots,\mathcal T) [hL;j;hR;(T+1−j)](j=1,2,⋯,T),构建神经网络对每对序列信息之间的关联关系进行评估:
每对序列具体是指h D ( t ) h_{\mathcal D}^{(t)} hD(t)与每一个[ h L ; j ; h R ; ( T + 1 − j ) ] \left[h_{\mathcal L;j};h_{\mathcal R;(\mathcal T+1-j)}\right] [hL;j;hR;(T+1−j)]配对并进行评估。配对的具体操作是将其拼接( Concatenate ) (\text{Concatenate}) (Concatenate)后作为线性计算层Attn \text{Attn} Attn的输入,并得到输出结果O ~ t j ( j = 1 , 2 , ⋯ , T ) \widetilde{\mathcal O}_{tj}(j=1,2,\cdots,\mathcal T) O tj(j=1,2,⋯,T)
{ O ~ t = ( O ~ t 1 , O ~ t 2 , ⋯ , O ~ t T ) T O ~ t j = Attn ( h D ( t ) , [ h L ; j ; h R ; ( T + 1 − j ) ] ) = W Attn ⋅ { Concat [ h D ( t ) , [ h L ; j ; h R ; ( T + 1 − j ) ] ] } + b Attn \begin{cases} \begin{aligned} \widetilde{\mathcal O}_t & = \left(\widetilde{\mathcal O}_{t1},\widetilde{\mathcal O}_{t2},\cdots,\widetilde{\mathcal O}_{t\mathcal T}\right)^T \\ \widetilde{\mathcal O}_{tj} & = \text{Attn} \left(h_{\mathcal D}^{(t)},\left[h_{\mathcal L;j};h_{\mathcal R;(\mathcal T+1-j)}\right]\right) \\ & = \mathcal W_{\text{Attn}} \cdot \left\{\text{Concat} \left[h_{\mathcal D}^{(t)},\left[h_{\mathcal L;j};h_{\mathcal R;(\mathcal T+1-j)}\right]\right]\right\} + b_{\text{Attn}} \end{aligned} \end{cases} ⎩ ⎨ ⎧O tO tj=(O t1,O t2,⋯,O tT)T=Attn(hD(t),[hL;j;hR;(T+1−j)])=WAttn⋅{Concat[hD(t),[hL;j;hR;(T+1−j)]]}+bAttn
- 对线性计算层输出 O ~ t \widetilde{\mathcal O}_t O t使用 Tanh \text{Tanh} Tanh激活函数进行映射;
O t = Tanh ( O ~ t ) \mathcal O_t = \text{Tanh}(\widetilde{\mathcal O}_t) Ot=Tanh(O t) - 构建神经网络层将 O t \mathcal O_t Ot中的每一个分量映射成标量信息,该信息的物理意义是: h D ( t ) h_{\mathcal D}^{(t)} hD(t)与所有编码器输出 [ h L ; j ; h R ; ( T + 1 − j ) ] ( j = 1 , 2 , ⋯ , T ) \left[h_{\mathcal L;j};h_{\mathcal R;(\mathcal T+1-j)}\right](j=1,2,\cdots,\mathcal T) [hL;j;hR;(T+1−j)](j=1,2,⋯,T)的评估分数。最后使用激活函数 Softmax \text{Softmax} Softmax,将该分数映射成比重结果:
E t = V T O t ⇒ ( e t 1 , e t 2 , ⋯ , e t T ) T s t j = Softmax ( e t j ) = exp ( e t j ) ∑ k = 1 T exp ( e t k ) S t = ( s t 1 , s t 2 , ⋯ , s t T ) T \begin{aligned} \mathcal E_t & = \mathcal V^T \mathcal O_t \\ & \Rightarrow (e_{t1},e_{t2},\cdots,e_{t\mathcal T})^T \\ s_{tj} & = \text{Softmax}(e_{tj})\\ & = \frac{\exp(e_{tj})}{\sum_{k=1}^{\mathcal T} \exp(e_{tk})} \\ \mathcal S_t & = (s_{t1},s_{t2},\cdots,s_{t\mathcal T})^T \end{aligned} EtstjSt=VTOt⇒(et1,et2,⋯,etT)T=Softmax(etj)=∑k=1Texp(etk)exp(etj)=(st1,st2,⋯,stT)T - 在得到 Softmax \text{Softmax} Softmax结果 S t \mathcal S_t St后,对 H B i = [ ( h L ; 1 ; h R ; T ) , ( h L ; 2 ; h R ; T − 1 ) , ⋯ , ( h L ; T ; h R ; 1 ) ] \mathcal H_{Bi} = \left[\left(h_{\mathcal L;1};h_{\mathcal R;\mathcal T}\right),\left(h_{\mathcal L;2};h_{\mathcal R;\mathcal T-1}\right),\cdots,\left(h_{\mathcal L;\mathcal T};h_{\mathcal R;1}\right)\right] HBi=[(hL;1;hR;T),(hL;2;hR;T−1),⋯,(hL;T;hR;1)]进行线性计算。即: S t \mathcal S_t St中的每一个分量与 H B i \mathcal H_{Bi} HBi对应结合,得到 C t \mathcal C_t Ct。
C t = [ S t ] T H B i \mathcal C_t = [\mathcal S_t]^T \mathcal H_{Bi} Ct=[St]THBi
注意力机制的简单描述
从心理学的角度观察,人类通常从刻意 ( Volitional ) (\text{Volitional}) (Volitional)信息与无意 ( Nonvolitional ) (\text{Nonvolitional}) (Nonvolitional)信息中选择注意点并进行获取。
-
刻意信息是指:自我主观想要获取的信息。例如:一张人脸图片中,我想要观察这个人的瞳孔颜色,而不是这个人的发量、性别等其他信息。
就像上面 Seq2seq \text{Seq2seq} Seq2seq注意力机制的例子,我们想要主观地认知 h D ( t ) h_{\mathcal D}^{(t)} hD(t)与编码器各时刻输出 [ h L ; j ; h R ; ( T + 1 − j ) ] \left[h_{\mathcal L;j};h_{\mathcal R;(\mathcal T+1-j)}\right] [hL;j;hR;(T+1−j)]之间的关联关系,而不仅仅是编码器产生的序列信息 C \mathcal C C。
-
而无意信息是指:相比于刻意信息,我们不经意间获取的信息。例如如下散点图:

很明显,我们注意到:这张图片中有一个红色的点。这并不是我们主观发现的,而是红色点区别于其他点的颜色性质使我们注意到了它。
很明显,刻意和无意信息在逻辑顺序上存在区别:
- 刻意:主动注意事物某一种属性 ⇒ \Rightarrow ⇒ 得到注意信息;
- 无意:事物原有的特点比较突出 ⇒ \Rightarrow ⇒ 从而该事物被注意到。
在深度学习中的一些操作仅考虑无意信息。例如:
- 卷积操作:它可能描述的是时间中其他过去时刻对该时刻的累积影响;或者是空间中,某图片周围像素点信息对中间像素点信息的累积影响。
- 全连接神经网络:对输入分布进行线性运算和非线性映射,将输入信息转化为抽象特征。
- 池化操作,如最大池化层 ( MaxPooling ) (\text{MaxPooling}) (MaxPooling)。该操作的思路在于:用一个值描述当前窗口信息的综合情况。
上述操作仅考虑无意信息的逻辑在于:它们对所有输入信息均一视同仁。也就是说,上述操作所得到的信息均归结于数据自身信息的性质。如:图像的边缘、明亮鲜艳的颜色等等。但这些信息并不是我们主观意识得到的信息。
相反, Seq2seq \text{Seq2seq} Seq2seq注意力机制中存在我们的主观意识,即刻意信息:在机器翻译任务中,刻意信息是指:某时刻的翻译结果与被翻译的句子中的某些词存在关联关系。
这里依然使用 Seq2seq \text{Seq2seq} Seq2seq注意力机制动机中的例子:
我 是 一名 演员 。 ⇔ I am an actor . \Leftrightarrow \text{I am an actor .} ⇔I am an actor .
关于 t = 3 t=3 t=3时刻翻译结果 an \text{ an } an 与原句之间存在如下关联关系:
其中原句中的‘一名’在英文中描述一个‘不定冠词’,但不定冠词中表示‘一个’的不定冠词有两种: a,an \text{a,an} a,an,但为什么选择 an \text{an} an而不是 a \text{a} a是因为‘演员’ actor \text{actor} actor开头是元音字母。因此,‘一名、演员’这两个词都对翻译结果 an \text{an} an产生了影响。

在深度学习中,刻意信息被称作查询向量 ( Query ) (\text{Query}) (Query);而环境信息(数据自身的信息)被描述成无意信息 ( Key ) (\text{Key}) (Key)与值 ( Value ) (\text{Value}) (Value)组成的键值对。
- 其中 Key \text{Key} Key和 Value \text{Value} Value可以是完全相同,完全相同意味着:主观意识没有对无意信息进行干预。
- 当然, Key \text{Key} Key和 Value \text{Value} Value也可以是不同的,不同的 Key,Value \text{Key,Value} Key,Value意味着:该无意信息根据主观意识进行描述产生的 Value \text{Value} Value,而不是无意信息自身。
而注意力机制,也称作注意力池化层 ( Attention Pooling ) (\text{Attention Pooling}) (Attention Pooling)。它的作用在于:基于查询向量 Query \text{Query} Query,从环境信息中有注意力偏向地选择出若干个键值对 ( Key-Value Pairs ) (\text{Key-Value Pairs}) (Key-Value Pairs)作为输出。其余的信息则不会输出出去。
注意力机制的机器学习范例: Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归
深度学习中的注意力机制确实是近 10 10 10年内的产物,但注意力机制自身并不是。早在 60 60 60年代提出一种非参数注意力的池化层—— Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归。
给定数据 D = { ( x ( i ) , y ( i ) ) } i = 1 N \mathcal D = \{(x^{(i)},y^{(i)})\}_{i=1}^N D={(x(i),y(i))}i=1N,对该数据做回归任务。它对应函数公式表示如下:
y ( i ) = 2 × sin ( x ( i ) ) + [ x ( i ) ] 0.8 + ϵ y^{(i)} = 2 \times \sin(x^{(i)}) + [x^{(i)}]^{0.8} + \epsilon y(i)=2×sin(x(i))+[x(i)]0.8+ϵ
其中 2 × sin ( x ( i ) ) + [ x ( i ) ] 0.8 2 \times \sin (x^{(i)}) + [x^{(i)}]^{0.8} 2×sin(x(i))+[x(i)]0.8表示真实分布 P d a t a \mathcal P_{data} Pdata的函数, ϵ ∼ N ( 0 , 0.5 ) \epsilon \sim \mathcal N(0,0.5) ϵ∼N(0,0.5)表示噪声信息。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)def f(x):return 2 * np.sin(x) + x ** 0.8SampleNum = 50
StandardX = np.linspace(0,5,200)
StandardY = [f(i) for i in StandardX]TrainX = [np.random.uniform(0,5) for _ in range(SampleNum)]
TrainY = [f(j) + np.random.normal(0.0,0.5) for j in TrainX]plt.plot(StandardX,StandardY,c="tab:blue")
plt.scatter(TrainX,TrainY,c="tab:orange")
plt.show()
对应训练数据(橙色点)以及真实函数(蓝色线)表示如下:

如果使用最简单的平均池化操作对标签进行预测。即:将所有训练数据对应标签取平均值。
f ( x ) = 1 N ∑ i = 1 N y ( i ) f(x) = \frac{1}{N} \sum_{i=1}^N y^{(i)} f(x)=N1i=1∑Ny(i)
基于该预测结果对应的函数图像表示如下(紫色虚线):

很明显,这就是一个极端欠拟合 ( Under-Fitting ) (\text{Under-Fitting}) (Under-Fitting)现象。也就是说:无论输入什么数据,预测结果均是该值。重新观察平均池化操作,我们发现:它对训练集内任意标签的权重(关注程度)均相同,为 1 N \begin{aligned}\frac{1}{N}\end{aligned} N1;
而 Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归描述了一种无参数注意力池化的思路:为训练集内不同样本的标签赋予不同的权重。
f ( x ) = ∑ i = 1 N κ ( x , x ( i ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( i ) f(x) = \sum_{i=1}^N \frac{\kappa(x,x^{(i)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(i)} f(x)=i=1∑N∑j=1Nκ(x,x(j))κ(x,x(i))⋅y(i)
其中, κ ( x , x ( i ) ) \kappa(x,x^{(i)}) κ(x,x(i))表示关于随机变量 x x x的核函数。在之前介绍过 κ ( x , x ( i ) ) \kappa(x,x^{(i)}) κ(x,x(i))描述的是:向量 x x x与 x ( i ) x^{(i)} x(i)被映射到高维空间后的内积结果:
κ ( x , x ( i ) ) = [ ϕ ( x ) ] T ⋅ ϕ ( x ( i ) ) \kappa(x,x^{(i)}) = [\phi(x)]^T \cdot \phi(x^{(i)}) κ(x,x(i))=[ϕ(x)]T⋅ϕ(x(i))
而内积大小描述的是余弦相似度。这意味着:核函数的结果描述样本之间的相似性。
回顾上式,将 f ( x ) f(x) f(x)展开:
f ( x ) = κ ( x , x ( 1 ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( 1 ) + κ ( x , x ( 2 ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( 2 ) + ⋯ + κ ( x , x ( N ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( N ) \begin{aligned} f(x) & = \frac{\kappa(x,x^{(1)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(1)} + \frac{\kappa(x,x^{(2)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(2)} + \cdots + \frac{\kappa(x,x^{(N)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(N)} \\ \end{aligned} f(x)=∑j=1Nκ(x,x(j))κ(x,x(1))⋅y(1)+∑j=1Nκ(x,x(j))κ(x,x(2))⋅y(2)+⋯+∑j=1Nκ(x,x(j))κ(x,x(N))⋅y(N)
可以看出:所有关于 y ( i ) ( i = 1 , 2 , ⋯ , N ) y^{(i)}(i=1,2,\cdots,N) y(i)(i=1,2,⋯,N)的系数,分母是相同的。那么这意味着:核函数的大小决定对应系数的大小。而系数的大小决定与对应向量 y ( i ) y^{(i)} y(i)注意力偏向的大小。
这里使用高斯核函数,也就是径向基核函数( Radial Basis Function,RBF \text{Radial Basis Function,RBF} Radial Basis Function,RBF)为例:
κ ( x , x ( j ) ) = exp { − 1 2 σ 2 ∣ ∣ x − x ( j ) ∣ ∣ 2 } \kappa(x,x^{(j)}) = \exp \left\{-\frac{1}{2\sigma^2} ||x - x^{(j)}||^2\right\} κ(x,x(j))=exp{−2σ21∣∣x−x(j)∣∣2}
其中 ∣ ∣ x − x ( j ) ∣ ∣ 2 ||x - x^{(j)}||^2 ∣∣x−x(j)∣∣2描述样本 x x x与样本 x ( j ) x^{(j)} x(j)之间的关联关系。以 ∣ ∣ x − x ( j ) ∣ ∣ 2 ||x - x^{(j)}||^2 ∣∣x−x(j)∣∣2作为自变量,观察 κ ( x , x ( j ) ) \kappa(x,x^{(j)}) κ(x,x(j))与自变量之间的关系:
import math
import numpy as np
import matplotlib.pyplot as pltdef RBF(x,sigma):return math.exp(-1 * (1 / (2 * (sigma ** 2))) * x)x = list(np.linspace(0,10,200))
y = [RBF(i,sigma=0.5) for i in x]
plt.plot(x,y)
plt.show()
返回结果表示如下:

很明显可以看出:以径向基核函数为前提的条件下,样本 x x x与某训练数据 x ( j ) x^{(j)} x(j)之间越接近(两者之间的差距越小, ∣ ∣ x − x ( j ) ∣ ∣ 2 → 0 ||x - x^{(j)}||^2 \rightarrow 0 ∣∣x−x(j)∣∣2→0),核函数结果越大,从而 Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归中,关于 y ( i ) y^{(i)} y(i)的系数越大。因此, Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归依然在求均值,只不过这次均值的权重包含了对各训练样本关联程度的注意力偏向。
从公式推导的角度也能看到其中的效果。将径向基核函数带入到上式中:
很明显,中间的系数项就是 Softmax \text{Softmax} Softmax函数的表达式。
f ( x ) = ∑ i = 1 N κ ( x , x ( i ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( i ) = ∑ i = 1 N exp { − 1 2 σ 2 ∣ ∣ x − x ( i ) ∣ ∣ 2 } ∑ j = 1 N exp { − 1 2 σ 2 ∣ ∣ x − x ( j ) ∣ ∣ 2 } ⋅ y ( i ) = ∑ i = 1 N Softmax [ − 1 2 σ 2 ∣ ∣ x − x ( i ) ∣ ∣ 2 ] ⋅ y ( i ) \begin{aligned} f(x) & = \sum_{i=1}^N \frac{\kappa(x,x^{(i)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(i)} \\ & = \sum_{i=1}^N \frac{\exp \left\{-\frac{1}{2\sigma^2} ||x - x^{(i)}||^2\right\}}{\sum_{j=1}^N \exp \left\{-\frac{1}{2\sigma^2} ||x - x^{(j)}||^2\right\}} \cdot y^{(i)} \\ & = \sum_{i=1}^N \text{Softmax} \left[-\frac{1}{2\sigma^2} ||x - x^{(i)}||^2\right] \cdot y^{(i)} \end{aligned} f(x)=i=1∑N∑j=1Nκ(x,x(j))κ(x,x(i))⋅y(i)=i=1∑N∑j=1Nexp{−2σ21∣∣x−x(j)∣∣2}exp{−2σ21∣∣x−x(i)∣∣2}⋅y(i)=i=1∑NSoftmax[−2σ21∣∣x−x(i)∣∣2]⋅y(i)
根据 Softmax \text{Softmax} Softmax函数的性质,上述操作相当于:将训练数据中的每个样本各自视作一个类别, Softmax \text{Softmax} Softmax结果相当于陌生样本对每个类别所归属的概率信息。并将该概率信息作为权重,执行带权重的均值计算。基于此,我们能够想到两种极端情况:
- 陌生样本 x x x与训练数据中的某样本 x ( j ) ( j ∈ { 1 , 2 , ⋯ , N } ) x^{(j)}(j \in \{1,2,\cdots,N\}) x(j)(j∈{1,2,⋯,N})重合。这意味着: Softmax \text{Softmax} Softmax函数的所有权重全部集中在 y ( j ) y^{(j)} y(j)上面。因而该样本 x x x的预测结果就是 y ( j ) y^{(j)} y(j);
- 陌生样本 x x x与所有训练数据 x ( j ) ( j = 1 , 2 , ⋯ , N ) x^{(j)}(j=1,2,\cdots,N) x(j)(j=1,2,⋯,N)都足够远(假设是无穷大),这导致 x x x关于所有 x ( j ) x^{(j)} x(j)的 Softmax \text{Softmax} Softmax系数均相同。从而该模型的预测结果就是平均值自身:
- Softmax \text{Softmax} Softmax
系数结果相同→ \rightarrow →既然核函数结果都是‘无限趋近与’0 0 0的值,它们之间的差别自然无关紧要。 取平均值可以理解为Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归最坏的预测情况。
f ( x ) = 1 N ∑ i = 1 N y ( i ) f(x) = \frac{1}{N} \sum_{i=1}^N y^{(i)} f(x)=N1i=1∑Ny(i)
- Softmax \text{Softmax} Softmax
从代码的角度描述 Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归的效果:
文章末尾附完整代码。
def NWKernelRegression(StandardX,TrainX,TrainY,Sigma):def RBF(x,xSample,Sigma):return math.exp(-1 * (1 / (2 * (Sigma ** 2))) * ((x - xSample) ** 2))def SoftmaxFunction(x,xSample,Sigma):return RBF(x,xSample,Sigma) / sum([RBF(x,i,Sigma) for i in TrainX])def NWKernelResult(x,Sigma):KernelResultList = list()for _,(xSample,ySample) in enumerate(zip(TrainX,TrainY)):SoftmaxCoeff = SoftmaxFunction(x,xSample,Sigma)KernelResultList.append(SoftmaxCoeff * ySample)return sum(KernelResultList)return [NWKernelResult(j,Sigma) for j in StandardX]
当超参数——高斯核函数的 σ = 0.5 \sigma=0.5 σ=0.5时,回归结果表示如下(绿色线):

当然,也可以继续调节 σ \sigma σ,找到一个更优秀的拟合效果甚至是过拟合效果:

可以发现:我们直接将陌生数据喂给训练集即可,没有显式的训练过程。这种处理方式被称作懒惰学习 ( Lazy Learning ) (\text{Lazy Learning}) (Lazy Learning)。之前介绍的另一种懒惰学习的代表—— K \mathcal K K近邻学习算法
Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归与注意力机制的关联
根据注意力机制的思路,可以将训练数据 D = { x ( i ) , y ( i ) } i = 1 N \mathcal D = \{x^{(i)},y^{(i)}\}_{i=1}^N D={x(i),y(i)}i=1N中,每个特征信息 x ( i ) ( i = 1 , 2 , ⋯ , N ) x^{(i)}(i=1,2,\cdots,N) x(i)(i=1,2,⋯,N)看做是无意信息 Key \text{Key} Key,而对应的 y ( i ) y^{(i)} y(i)则表示每个键值对 Key \text{Key} Key对应的 Value \text{Value} Value信息。
而每一个陌生样本 x x x被视作 Query \text{Query} Query,原因是:我们想要主观获取 Query \text{Query} Query与各个 Key \text{Key} Key之间的关联关系。这个关联关系的分布就是 Softmax \text{Softmax} Softmax构成的序列向量:
G [ Query ( x ) , Key ( x ( 1 ) , x ( 2 ) , ⋯ , x ( N ) ) ] = [ κ ( x , x ( 1 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , κ ( x , x ( 2 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , ⋯ , κ ( x , x ( N ) ) ∑ j = 1 N κ ( x , x ( j ) ) ] N × 1 T \mathcal G \left[\text{Query}(x),\text{Key}(x^{(1)},x^{(2)},\cdots,x^{(N)})\right] = \left[\frac{\kappa(x,x^{(1)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\frac{\kappa(x,x^{(2)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\cdots,\frac{\kappa(x,x^{(N)})}{\sum_{j=1}^N \kappa(x,x^{(j)})}\right]_{N \times 1}^T G[Query(x),Key(x(1),x(2),⋯,x(N))]=[∑j=1Nκ(x,x(j))κ(x,x(1)),∑j=1Nκ(x,x(j))κ(x,x(2)),⋯,∑j=1Nκ(x,x(j))κ(x,x(N))]N×1T
最终将注意力分布 G \mathcal G G与各个 Key \text{Key} Key对应的 Value \text{Value} Value相结合,得到注意力结果:
f ( x ) = { G [ Query ( x ) , Key ( x ( 1 ) , x ( 2 ) , ⋯ , x ( N ) ) ] } T ⋅ Value ( y ( 1 ) , y ( 2 ) , ⋯ , y ( N ) ) = [ κ ( x , x ( 1 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , κ ( x , x ( 2 ) ) ∑ j = 1 N κ ( x , x ( j ) ) , ⋯ , κ ( x , x ( N ) ) ∑ j = 1 N κ ( x , x ( j ) ) ] 1 × N ( y ( 1 ) y ( 2 ) ⋮ y ( N ) ) N × 1 = ∑ i = 1 N κ ( x , x ( i ) ) ∑ j = 1 N κ ( x , x ( j ) ) ⋅ y ( i ) \begin{aligned} f(x) & = \left\{\mathcal G \left[\text{Query}(x),\text{Key}(x^{(1)},x^{(2)},\cdots,x^{(N)})\right]\right\}^T \cdot \text{Value}(y^{(1)},y^{(2)},\cdots,y^{(N)}) \\ & = \left[\frac{\kappa(x,x^{(1)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\frac{\kappa(x,x^{(2)})}{\sum_{j=1}^N \kappa(x,x^{(j)})},\cdots,\frac{\kappa(x,x^{(N)})}{\sum_{j=1}^N \kappa(x,x^{(j)})}\right]_{1 \times N} \begin{pmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(N)} \end{pmatrix}_{N \times 1} \\ & = \sum_{i=1}^N \frac{\kappa(x,x^{(i)})}{\sum_{j=1}^N \kappa(x,x^{(j)})} \cdot y^{(i)} \end{aligned} f(x)={G[Query(x),Key(x(1),x(2),⋯,x(N))]}T⋅Value(y(1),y(2),⋯,y(N))=[∑j=1Nκ(x,x(j))κ(x,x(1)),∑j=1Nκ(x,x(j))κ(x,x(2)),⋯,∑j=1Nκ(x,x(j))κ(x,x(N))]1×N y(1)y(2)⋮y(N) N×1=i=1∑N∑j=1Nκ(x,x(j))κ(x,x(i))⋅y(i)
附: Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归示例完整代码
import numpy as np
import math
import matplotlib.pyplot as plt
np.random.seed(42)def f(x):return 2 * np.sin(x) + x ** 0.8def Average(TrainY):return [float(np.mean(TrainY)) for _ in range(200)]def NWKernelRegression(StandardX,TrainX,TrainY,Sigma):def RBF(x,xSample,Sigma):return math.exp(-1 * (1 / (2 * (Sigma ** 2))) * ((x - xSample) ** 2))def SoftmaxFunction(x,xSample,Sigma):return RBF(x,xSample,Sigma) / sum([RBF(x,i,Sigma) for i in TrainX])def NWKernelResult(x,Sigma):KernelResultList = list()for _,(xSample,ySample) in enumerate(zip(TrainX,TrainY)):SoftmaxCoeff = SoftmaxFunction(x,xSample,Sigma)KernelResultList.append(SoftmaxCoeff * ySample)return sum(KernelResultList)return [NWKernelResult(j,Sigma) for j in StandardX]SampleNum = 50
StandardX = np.linspace(0,5,200)
StandardY = [f(i) for i in StandardX]TrainX = [np.random.uniform(0,5) for _ in range(SampleNum)]
TrainY = [f(j) + np.random.normal(0.0,0.5) for j in TrainX]
AveragePred = Average(TrainY)
NWKernelPred1 = NWKernelRegression(StandardX,TrainX,TrainY,Sigma=0.01)
NWKernelPred2 = NWKernelRegression(StandardX,TrainX,TrainY,Sigma=0.25)plt.plot(StandardX,StandardY,c="tab:blue",label="Standard")
plt.plot(StandardX,AveragePred,c="#9900ff",linestyle="--",label="AveragePred")
plt.plot(StandardX,NWKernelPred1,c="tab:green",linestyle="--",label="NWPred sigma=0.01")
plt.plot(StandardX,NWKernelPred2,c="tab:red",linestyle="--",label="NWPred sigma=0.25")
plt.scatter(TrainX,TrainY,c="tab:orange")
plt.legend(loc=0)
plt.show()
相关参考:
64 注意力机制【动手学深度学习v2】
注意力汇聚:Nadaraya-Watson 核回归
相关文章:

深度学习笔记之Transformer(一)注意力机制基本介绍
深度学习笔记之Transformer——注意力机制基本介绍 引言回顾: Seq2seq \text{Seq2seq} Seq2seq模型中的注意力机制注意力机制的简单描述注意力机制的机器学习范例: Nadaraya-Watson \text{Nadaraya-Watson} Nadaraya-Watson核回归 Nadaraya-Watson \text…...

基于SpringBoot的SSM整合案例 -- SpringBoot快速入门保姆级教程(四)
文章目录 前言1.设计创建数据库表tbl_book2.创建新的SpringBoot模块,勾选相关依赖3. 添加SpringBoot创建项目时没有提供的相关坐标4.根据数据库表创建实体类Book5.编写dao层操作BookDao6.编写Service服务层接口BookService7.编写服务层实现类BookServiceImpl8.编写B…...

占据80%中国企业出海市场,亚马逊云科技如何为出海客户提供更多资源和附加值
亚马逊云科技就可以做到,作为占据80%中国企业出海市场的亚马逊云科技,其覆盖全球的业务体系,从亚马逊海外购、亚马逊全球开店、亚马逊智能硬件与服务,Amazon Alexa,Amazon Music都是属于亚马逊云科技“梦之队”的一员。…...

系统架构设计师笔记第11期:信息安全的抗攻击技术
拒绝服务攻击 拒绝服务攻击(Denial of Service,DoS)是一种旨在使目标系统无法提供正常服务的攻击方式。攻击者通过向目标系统发送大量的请求或占用系统资源,超过系统的承载能力,导致系统过载或崩溃,从而使…...
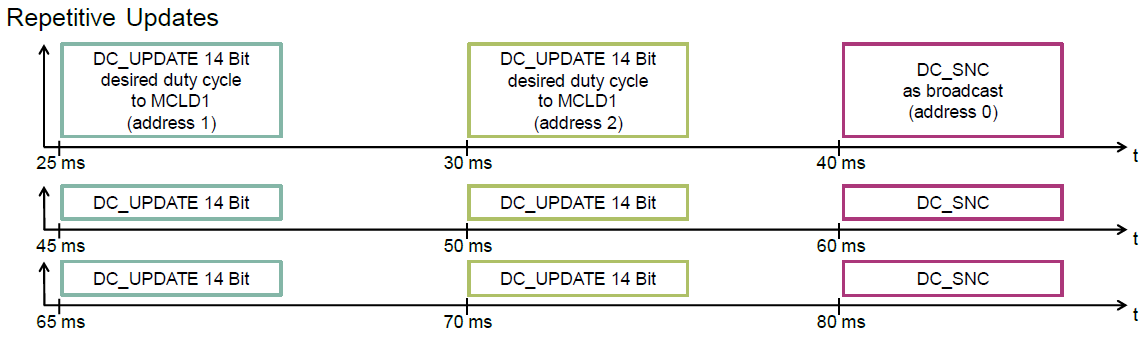
TLD7002学习笔记(二)-使用S32K144驱动TLD7002
文章目录 1. 前言2. 评估板简介3. 官方驱动3.1 官网驱动的介绍3.2 官方驱动的移植3.3 官方驱动的使用 4. 参考资料 1. 前言 本篇文章是TLD7002学习笔记的第二篇,主要是介绍如何使用S32K144驱动TLD7002-16ES。为此,笔者做了一套基于TLD7002-16ES的评估板…...

[元带你学: eMMC协议详解 14] 数据擦除(Erase) 详解
依JEDEC eMMC 5.1及经验辛苦整理,付费内容,禁止转载。 所在专栏 《元带你学: eMMC协议详解》 内容摘要 全文 4200字, 主要内容介绍了各种擦除操作概念以记用法,总结了不同擦除操作的区别, 根据不同安全级别和应用场景…...

【程序人生-Hello‘s P2P】哈尔滨工业大学深入理解计算机系统大作业
计算机系统 大作业 题 目 程序人生-Hello’s P2P 专 业 xxxx 学 号 2021xxxx 班 级 210xxxx 学 生 xx 指 导 教 师 xxx 计算机科学与技术学院 2023年5月 摘 要 HelloWorld是每个程序员接触的第一个程序,表面上平平无奇的它背后却是由操作系统许多设计精巧的机制支撑…...

Android Studio入门
首先确保系统已经安装好JDK和Android SDK Android SDK的安装有两种方案 方案一:直接下载包安装 官网下载 国内下载 方案二:使用命令行工具进行安装 在Android Studio官网下载Command line tools 最新:如果使用 Android Studio,…...
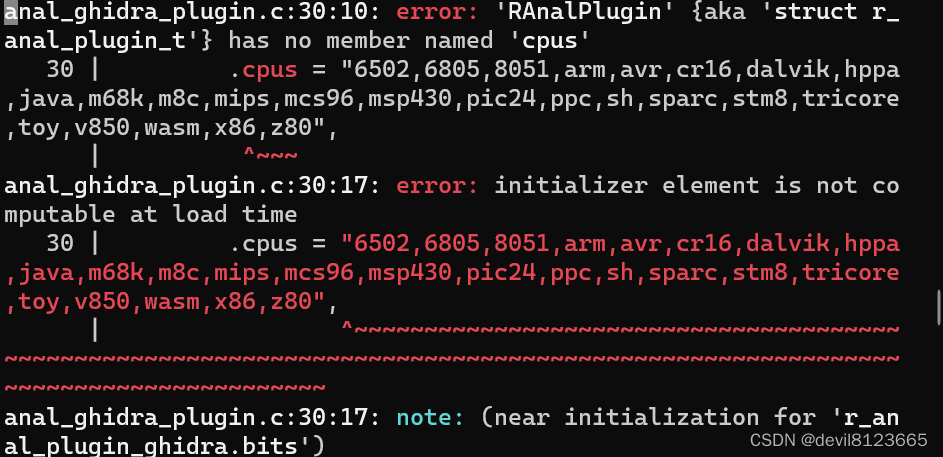
r2pm -ci r2ghidra 时报错:checking pkg-config flags for r_core... no
参考网址: sys/python.sh fails with checking pkg-config flags for r_core... no Issue #1943 radareorg/radare2 GitHub 进入目录/root/.local/share/radare2/r2pm/git/r2ghidra查看configure文件,查找报错位置 执行指令 : # pkg-co…...
【宿舍管理系统】注册登录页面的实现(前端)
目录 一.创建一个jsp文件,命名为login.jsp 代码: 1. 2. 3. 4. 5. 6. 编辑 二. 创建一个css文件,并命名为style.css 1. 编辑效果如下: 编辑 代码解析: 2. 效果如下: 代码解析࿱…...
 言简意赅傻瓜式写法)
python写入excel,(二) 言简意赅傻瓜式写法
xlrd限制条数,openpyxl 上限较高,所以推荐这种写法 import openpyxl # openpyxl引入模块 def write_to_excel(path: str, sheetStr, info, data): # 实例化一个workbook对象 workbook openpyxl.Workbook() # 激活一个sheet …...
:北京卷II)
我用ChatGPT写2023高考语文作文(六):北京卷II
2023年 北京卷 II 适用地区:北京 舞台上,戏曲演员有登场亮相的瞬间。生活中也有许多亮相时刻:国旗下的讲话,研学成果的汇报,新产品的发布……每一次亮相,都受到众人关注;每一次亮相,…...

Vue中如何进行图表绘制
Vue中如何进行图表绘制 数据可视化是Web应用中非常重要的一部分,其中图表绘制是其中的重要环节。Vue作为一款流行的前端框架,提供了很多优秀的图表库,以满足不同业务场景下的需求。本文将介绍如何在Vue中进行图表绘制,包括使用Vu…...
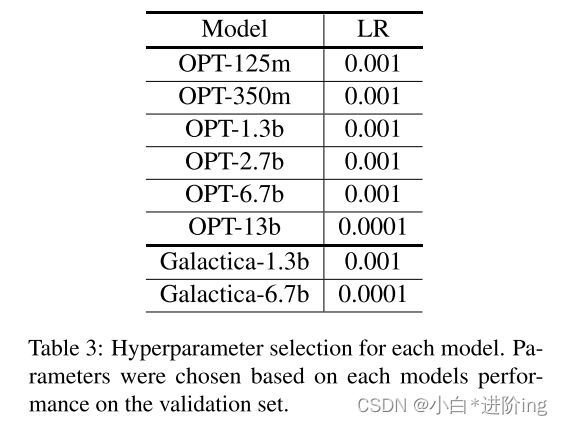
【Soft-prompt Tuning for Large Language Models to Evaluate Bias 论文略读】
Soft-prompt Tuning for Large Language Models to Evaluate Bias 论文略读 INFORMATIONAbstract1 Introduction2 Related work3 Methodology3.1 Experimental setup 4 Results5 Discussion & Conclusion总结A Fairness metricsB Hyperparmeter DetailsC DatasetsD Prompt …...

Qt 定时器与定时事件
一、定时器 在头文件.h中进行声明: private slots:void timeOut(); // 定时器超时槽函数在.cpp中进行实现相应的功能: // 构造函数 Widget::Widget(QWidget *parent) :QWidget(parent),ui(new Ui::Widget) {ui->setupUi(this);// 创建一个新的定时…...
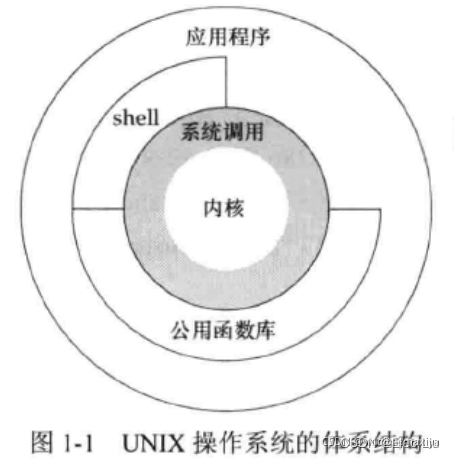
《UNUX环境高级编程》(1)UNIX基础
1、引言 2、UNIX体系结构 操作系统 一种软件,控制计算机硬件资源,提供程序运行环境。操作系统包含了内核和一些其他软件(如shell、公用函数库、应用程序等)。例如Linux就是GNU操作系统的内核,因此也称为GNU/Linux操作…...

MATLAB 入门之旅摘要
matlab官方基础课程,重温或者入门都是不错的选择。 MATLAB 入门之旅 MATLAB 入门之旅 | 自定进度在线课程 - MATLAB & Simulink 基本语法 示例说明x pi使用等号 () 创建变量。 左侧 (x) 是变量的名称,其值为右侧 (pi) 的值。y sin(-5)您可以使用括…...

chatgpt赋能python:Python小数运算:解决精度问题的最佳实践
Python小数运算:解决精度问题的最佳实践 在进行小数运算时,Python是一种十分常用的语言,但在进行小数运算时,由于二进制和十进制之间的转换不完全,可能会导致一些精度问题。为了避免这些问题,让我们一起了…...

Linux 安装Docker完整教程(六)
文章目录 背景一、Docker简介二、docker desktop 和 docker engin 区别三、Linux 安装Docker1. 安装docker的前置条件:2. 查看Docker版本3. 检查是否安装过Docker4. Docker自动化安装 (不想自带化安装的可跳过本步骤,选择手动安装)5. Docker手动安装&…...
手机连接adb 相关问题汇总
目录 关于端口占用问题1 关于修改adb 端口配置问题2 方法3 方法4 关于端口占用问题1 转载链接:https://www.jianshu.com/p/902a89b06271 报错信息: error: no device/emulators found error: device still connecting 解决方案: 重启…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
