原码反码补码
在计算机中,负数都是以补码的形式存放的,
正数的原码、反码、补码完全一致。
- 原码:指的是正数的二进制或负数的二进制,
负数的二进制(原码),其实就是在正数的二进制的最高位前面加一个符号位 1。 作者:LI_IR https://www.bilibili.com/read/cv11272331 出处:bilibili
- 求反码:对于正数,其反码和原码相同;对于负数,则将其原码的符号位 1 保持不变,而将其他位按位取反(即将 0 换为 1,将 1 换为 0)。
- 求补码:对于正数,其补码和原码相同;对于负数,负数的补码是反码加 1。若对一补码再次求补,就又得到了对应的原码。 作者:LI_IR https://www.bilibili.com/read/cv11272331 出处:bilibili
计算负数的补码有两种方法:
- 负数所对应的正数的补码的相反数:先求负数所对应的正数的二进制,然后再取反,再加 1,就得到了负数的补码,这也是负数在计算机中的存储形式。 作者:LI_IR https://www.bilibili.com/read/cv11272331 出处:bilibili
- 负数的补码是反码加 1
第一种方法计算示例
- 1 的原码、反码、补码为 0000 0001
- 取反为 1111 1110
- 加 1 为 1111 1111, 计算机存负 1 的形式
第二种方法计算示例
- -1 的原码为 1000 0001
- -1 的反码为 1111 1110
- -1 的补码为 1111 1111,计算机存储负 1 的形式
这两种方式计算结果一致是因为,正数的原码取反会把符号位上的 0 反成 1,而负数计算反码,符号位上的 1 保持不变
-128 的二进制是 110000000(注意:-128 占了 9 位,超出了一个字节),然后按照上面的规则求其补码,先求反码(符号位保持不变,其他位取反),再加 1,结果为 110000000,发现与原来一样,若用一个字节来存储,那就是 10000000(把高位给截掉),也就是说,-128 在计算机存储时是以 10000000(补码)的形式存储的,在计算机中它就表示-128。 作者:LI_IR https://www.bilibili.com/read/cv11272331 出处:bilibili
相关文章:

原码反码补码
在计算机中,负数都是以补码的形式存放的, 正数的原码、反码、补码完全一致。 原码:指的是正数的二进制或负数的二进制, 负数的二进制(原码),其实就是在正数的二进制的最高位前面加一个符号位 1。…...
大数据选股智能推荐系统V1.0-1
很长时间没有发布博客了,这段时间个人确实有点忙。另外一方面在这段时间我也没有闲着。自己研发了一套大数据选股的智能推荐系统。废话不说,我们先来看这套系统:登录页面:(技术点:验证码的生成)…...

调研生成GIF表情包之路
调研阶段 gifshot.js合成GIF 可以从媒体流、视频或图像创建动画 GIF 的 JavaScript 库。 csdn地址:https://blog.csdn.net/qq_16494241/article/details/125717405 分解GIF图片、合成GIF图片 两步走: 1、分解GIF图片 libgif-js:JavaScrip…...

【RocketMQ】源码详解:生产者启动与消息发送流程
消息发送 生产者启动 入口 : org.apache.rocketmq.client.impl.producer.DefaultMQProducerImpl#start(boolean) 生产者在调用send()方法发送消息之前,需要调用start进行启动, 生产者启动过程中会启动一些服务和线程 启动过程中会启动MQClientInstance, 这个实例是针对一个项…...
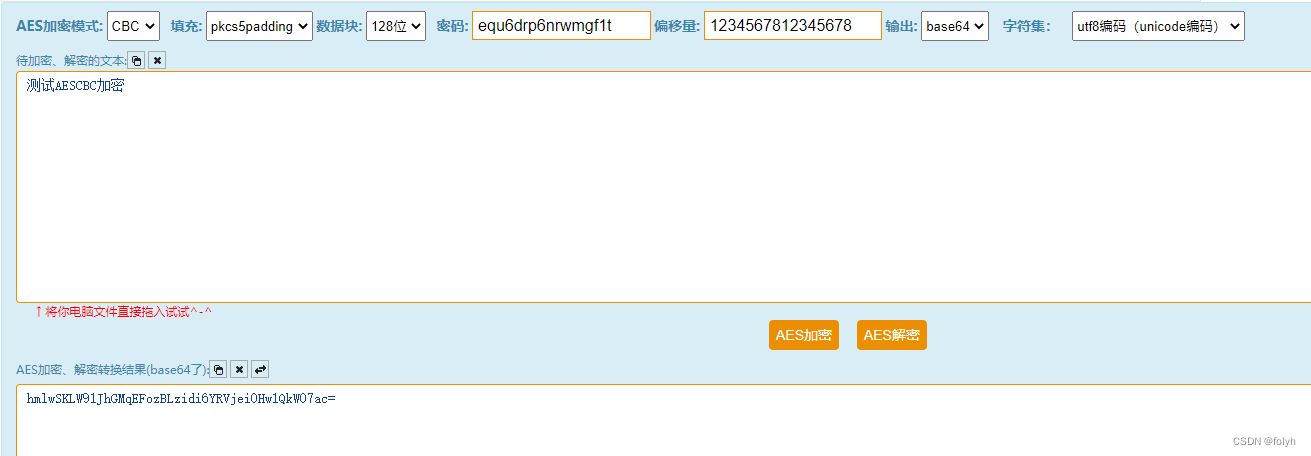
信息安全(一)
思维导图 一、AES加解密 1.概述 1.1 概念 AES: 高级加密标准(Advanced Encryption Standard)是一种对称加密的区块加密标准。 (1)替代DES的新一代分组加密算法 (2)支持三种长度密钥&#x…...

企业多会场视频直播(主会场、分会场直播)实例效果
阿酷TONY 2023-2-16 长沙 活动直播做多会场切换功能(主会场、分会场、会场一、会场二、会场三自由切换) 企业多会场视频直播(主会场、分会场直播)实例效果 特点:支持PC端,也支持移动端观看,会…...
行列式)
线性代数速览(一)行列式
文章目录行列式🌻 行列式的定义🌼 行列式的性质🌷 一些定理🥀 行列式的计算🌺 克莱姆法则行列式 行列式的本质,就是一个数值。 🌻 行列式的定义 有三种定义:1、按行展开ÿ…...

恭喜山东翰林“智慧园区管理系统”获易知微可视化设计大赛二等奖
数字化经济发展是全球经济发展的重中之重,“数字孪生(Digital Twin)”这一词汇正在成为学术界和产业界的一个热点。数字孪生作为近年来的新兴技术,其与国民经济各产业融合不断深化,推动着各大产业数字化、网络化、智能…...

gulp简单使用
gulp gulp的核心理念是task runner 可以定义自己的一系列任务 等待任务被执行 基于文件stream的构建流 我们可以使用gulp的插件体系来完成某些任务 webpack的核心理念是module bundler webpack是一个模块化的打包工具 可以使用各种各样的loader来加载不同的模块 可以使用各种…...

ce认证机构如何选择?
CE认证想必大家都已经有所了解,它是产品进入欧盟销售的通行证,那么我们在办理CE认证时该怎么进行选择?带大家了解一下CE认证机构,以及该怎么去进行选择? 以下信息由证果果编辑整理,更多认证机构信息请到证果果网站查看。找机构…...

全网招募P图高手!阿里巴巴持续训练鉴假AI
P过的证件如何鉴定为真?三千万网友都晒出了与梅西的合影?图像编辑技术的普及让人人都能P图,但也带来“假图”识别难题,甚至是欺诈问题。 为此,阿里安全联合华中科技大学国家防伪工程中心、国际文档分析识别方向的唯一顶…...
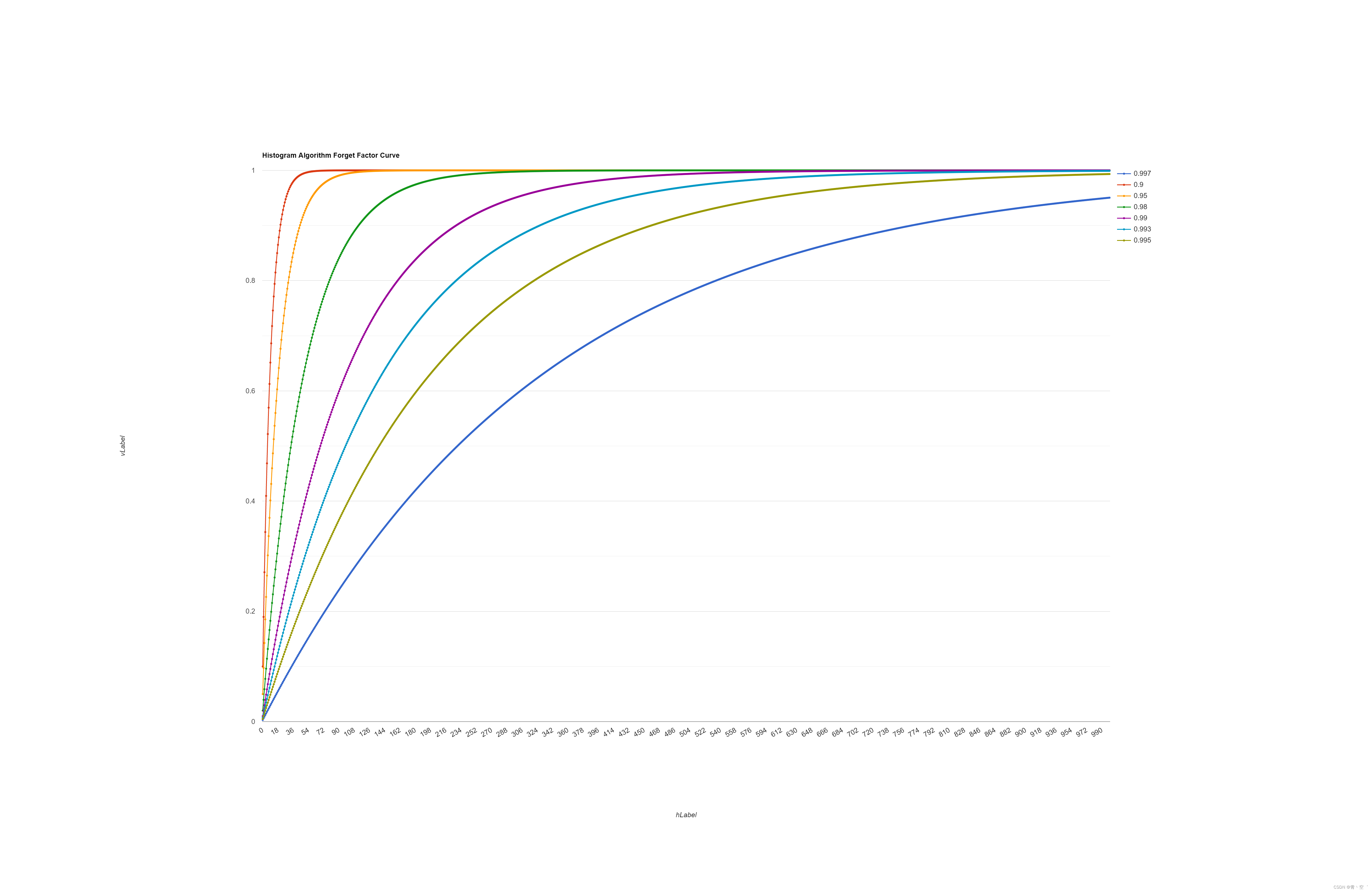
webrtc QOS笔记一 Neteq直方图算法浅读
webrtc QOS笔记一 Neteq直方图算法浅读 文章目录webrtc QOS笔记一 Neteq直方图算法浅读Histogram Algorithm获取目标延迟遗忘因子曲线Histogram Algorithm DelayManager::Update()->Histogram::Add() 会根据计算的iat_packet(inter arrival times, 实际包间间隔 / 打包时长…...

细分和切入点
本文重点介绍做SEO网站细分和切入点的方法:当我们的行业和关键词竞争性比较大的时候,我们可以考虑对行业或者产品做细分,从而找到切入点。可以按照以下三个方面进行细分。1、按城市细分例如:A:餐饮培训,当前…...
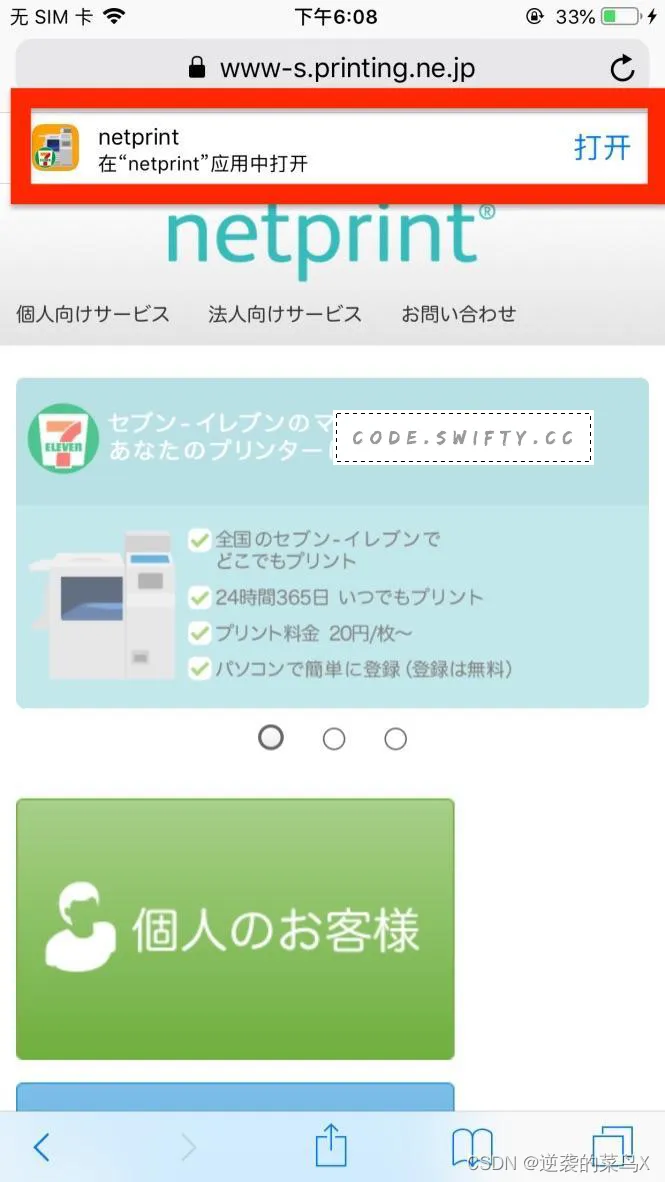
iOS创建Universal Link
iOS 9之前,一直使用的是URL Schemes技术来从外部对App进行跳转,但是iOS系统中进行URL Schemes跳转的时候如果没有安装App,会提示无法打开页面的提示。 iOS 9之后起可以使用Universal Links技术进行跳转页面,这是一种体验更加完美的…...

RuoYi-Vue搭建(若依)
项目简介 RuoYi-Vue基于SpringBootVue前后端分离的Java快速开发框架1.前端采用Vue、Element UI2.后端采用Spring Boot、Spring Security、Redis & Jwt3.权限认证使用Jwt,支持多终端认证系统4.支持加载动态权限菜单,多方式轻松权限控制5.高效率开发&a…...
进程组和用处
进程组:一个或多个进程的集合,进程组id是一个正整数。组长进程:进程组id 进程id组长进程可以创建一个进程组,创建该进程组的进程,终止了,只要进程组有一个进程存在,进程组就存在,与…...

Nacos集群+Nginx负载均衡
搭建Nacos集群 注意: 3个或3个以上Nacos节点才能构成集群。要求服务器内存分配最好大于6G以上(如果不够则需修改nacos启动脚本中的默认内存配置)根据nacos自带的mysql建库脚本建立对应数据库(/conf/nacos-mysql.sql)如果是三台服…...

TypeScript 学习之类型兼容
TypeScript 的类型兼容性是基于结构子类型的。 结构类型是一种只使用其成员来描述类型的方式。 interface Named {name: string; }class Person {name: string; }let p: Named; p new Person();// 赋值成功,因为都是结构类型,只要Person 类型的包含 Nam…...

Linux软件管理RPM
目录 前言 RPM软件管理程序:rpm RPM默认安装的路径 PRM讲解前准备工作 RPM安装(install) RPM查询(query) RPM卸载(erase) RPM升级与更新(upgrade/freshen) RPM重…...

01背包问题
背包问题的递归解决过程如下: 第一步明确思路 在解决问题之前,为描述方便,首先定义一些变量:Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...
