线性代数速览(一)行列式
文章目录
- 行列式
- 🌻 行列式的定义
- 🌼 行列式的性质
- 🌷 一些定理
- 🥀 行列式的计算
- 🌺 克莱姆法则
行列式
行列式的本质,就是一个数值。
🌻 行列式的定义
有三种定义:1、按行展开;2、按列展开;3、即不按行,也不按列的展开。
按行展开时,行标取标准排列,列标取所有可能。
∣a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮an1an2⋯ann∣=∑j1j2...jn(−1)N(j1j2...jn)aij1aij2...aijn\left| \begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{array} \right| =\sum_{j_1j_2...j_n}(-1)^{N(j_1j_2...j_n)}a_{ij_1}a_{ij_2}...a_{ij_n} ∣∣∣∣∣∣∣∣∣a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann∣∣∣∣∣∣∣∣∣=j1j2...jn∑(−1)N(j1j2...jn)aij1aij2...aijn
🌼 行列式的性质
1、转置
转置不会改变行列式的值。
推论:对行成立的性质,对列也成立。
DT=DD^T=DDT=D
2、对换
对换两行,行列式的值变号
∣123456789∣=−∣456123789∣\left| \begin{array}{cccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array} \right|=- \left| \begin{array}{cccc} 4 & 5 & 6 \\ 1 & 2 & 3 \\ 7 & 8 & 9 \end{array} \right| ∣∣∣∣∣∣147258369∣∣∣∣∣∣=−∣∣∣∣∣∣417528639∣∣∣∣∣∣
3、行相等
行列式中存在两行对应元素相等时,行列式的值为0。
∣123456123∣=0\left| \begin{array}{cccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 1 & 2 & 3 \end{array} \right|=0 ∣∣∣∣∣∣141252363∣∣∣∣∣∣=0
4、提因子
某一行元素都乘以k,等于用k乘以D。
∣123224789∣=2∣123112789∣\left| \begin{array}{cccc} 1 & 2 & 3 \\ 2 & 2 & 4 \\ 7 & 8 & 9 \end{array} \right|=2 \left| \begin{array}{cccc} 1 & 2 & 3 \\ 1 & 1 & 2 \\ 7 & 8 & 9 \end{array} \right| ∣∣∣∣∣∣127228349∣∣∣∣∣∣=2∣∣∣∣∣∣117218329∣∣∣∣∣∣
5、行成比例
两行元素对应成比例,则行列式值为0。
∣123456246∣=0\left| \begin{array}{cccc} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 2 & 4 & 6 \end{array} \right|=0 ∣∣∣∣∣∣142254366∣∣∣∣∣∣=0
推论:某一行全为0,则行列式值为0。
6、可拆性
只拆一行,其余行保持不变。
∣1237+82+39+10889∣=∣123729889∣+∣1238310889∣\left| \begin{array}{cccc} 1 & 2 & 3 \\ 7+8 & 2+3 & 9+10 \\ 8 & 8 & 9 \end{array} \right|= \left| \begin{array}{cccc} 1 & 2 & 3 \\ 7 & 2 & 9 \\ 8 & 8 & 9 \end{array} \right|+ \left| \begin{array}{cccc} 1 & 2 & 3 \\ 8 & 3 & 10 \\ 8 & 8 & 9 \end{array} \right| ∣∣∣∣∣∣17+8822+3839+109∣∣∣∣∣∣=∣∣∣∣∣∣178228399∣∣∣∣∣∣+∣∣∣∣∣∣1882383109∣∣∣∣∣∣
7、行间相加
某一行乘以一个数,加到另一行上去,行列式的值不变。
🌷 一些定理
1、按某行展开
按一行展开,有降阶效果。例如按第 i 行展开,每一项都是元素乘以对应的代数余子式。
D=ai1Ai1+ai2Ai2+ai3Ai3+...+ainAinD=a_{i1}A_{i1}+a_{i2}A_{i2}+a_{i3}A_{i3}+...+a_{in}A_{in}D=ai1Ai1+ai2Ai2+ai3Ai3+...+ainAin
2、异乘变零
某行元素与另一行元素的代余式成绩之和等于零。
ai1Aj1+ai2Aj2+ai3Aj3+...+ainAjn=0(i≠j)a_{i1}A_{j1}+a_{i2}A_{j2}+a_{i3}A_{j3}+...+a_{in}A_{jn}=0(i\not=j)ai1Aj1+ai2Aj2+ai3Aj3+...+ainAjn=0(i=j)
3、拉普拉斯
取定 k 行,有 k 行元素组成的所有 k 阶子式与代数余子式乘积之和等于D。
4、行列式相乘
同阶行列式相乘时,规则同矩阵乘法。非同阶就分别计算两个行列式的值,然后相乘好了。
🥀 行列式的计算
两种基本的计算思路:
- 化成上三角行列式
- 按某一行(零多的一行)展开
然后就是一些特殊的行列式的解法(略)。
1、对角型
∣xaaaxaaax∣\left| \begin{array}{cccc} x & a & a \\ a & x & a \\ a & a & x \end{array} \right| ∣∣∣∣∣∣xaaaxaaax∣∣∣∣∣∣
2、三叉型
∣x1b1b2b3a1x200a20x30a300x4∣\left| \begin{array}{cccc} x_1 & b_1 & b_2 & b_3\\ a_1 & x_2 & 0 & 0 \\ a_2 & 0 & x_3 & 0 \\ a_3 & 0 & 0 & x_4 \end{array} \right| ∣∣∣∣∣∣∣∣x1a1a2a3b1x200b20x30b300x4∣∣∣∣∣∣∣∣
3、范德蒙德
∣111x1x2x3x12x22x32∣\left| \begin{array}{cccc} 1 & 1 & 1 \\ x_1 & x_2 & x_3 \\ x_1^2 & x_2^2 & x_3^2 \end{array} \right| ∣∣∣∣∣∣1x1x121x2x221x3x32∣∣∣∣∣∣
🌺 克莱姆法则
用于解方程组,但计算量大一般不用。
定理:“齐次线性方程组有非零解“是”系数行列式的值为零“的充分必要条件。
相关文章:
行列式)
线性代数速览(一)行列式
文章目录行列式🌻 行列式的定义🌼 行列式的性质🌷 一些定理🥀 行列式的计算🌺 克莱姆法则行列式 行列式的本质,就是一个数值。 🌻 行列式的定义 有三种定义:1、按行展开ÿ…...

恭喜山东翰林“智慧园区管理系统”获易知微可视化设计大赛二等奖
数字化经济发展是全球经济发展的重中之重,“数字孪生(Digital Twin)”这一词汇正在成为学术界和产业界的一个热点。数字孪生作为近年来的新兴技术,其与国民经济各产业融合不断深化,推动着各大产业数字化、网络化、智能…...

gulp简单使用
gulp gulp的核心理念是task runner 可以定义自己的一系列任务 等待任务被执行 基于文件stream的构建流 我们可以使用gulp的插件体系来完成某些任务 webpack的核心理念是module bundler webpack是一个模块化的打包工具 可以使用各种各样的loader来加载不同的模块 可以使用各种…...

ce认证机构如何选择?
CE认证想必大家都已经有所了解,它是产品进入欧盟销售的通行证,那么我们在办理CE认证时该怎么进行选择?带大家了解一下CE认证机构,以及该怎么去进行选择? 以下信息由证果果编辑整理,更多认证机构信息请到证果果网站查看。找机构…...

全网招募P图高手!阿里巴巴持续训练鉴假AI
P过的证件如何鉴定为真?三千万网友都晒出了与梅西的合影?图像编辑技术的普及让人人都能P图,但也带来“假图”识别难题,甚至是欺诈问题。 为此,阿里安全联合华中科技大学国家防伪工程中心、国际文档分析识别方向的唯一顶…...
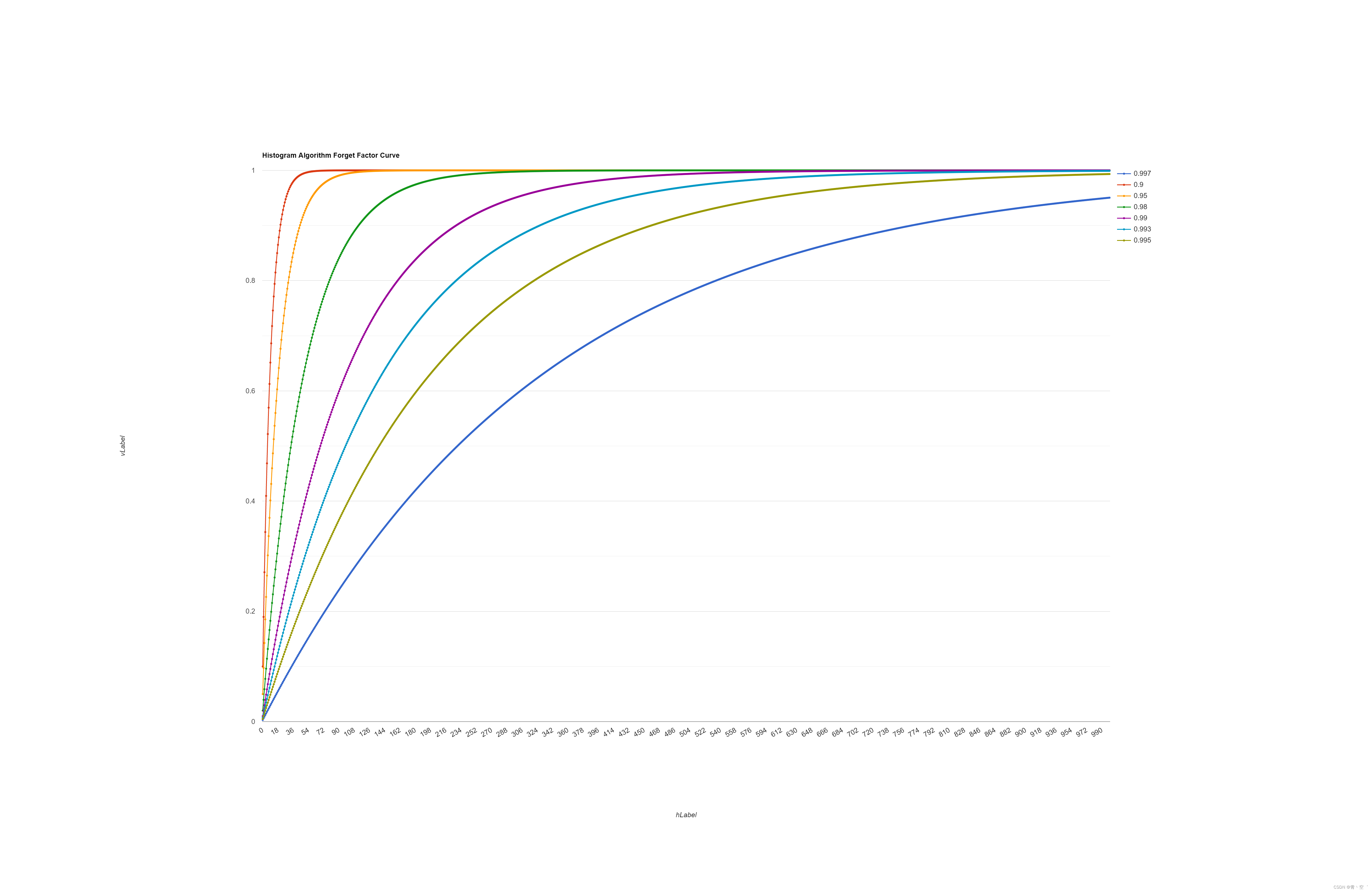
webrtc QOS笔记一 Neteq直方图算法浅读
webrtc QOS笔记一 Neteq直方图算法浅读 文章目录webrtc QOS笔记一 Neteq直方图算法浅读Histogram Algorithm获取目标延迟遗忘因子曲线Histogram Algorithm DelayManager::Update()->Histogram::Add() 会根据计算的iat_packet(inter arrival times, 实际包间间隔 / 打包时长…...

细分和切入点
本文重点介绍做SEO网站细分和切入点的方法:当我们的行业和关键词竞争性比较大的时候,我们可以考虑对行业或者产品做细分,从而找到切入点。可以按照以下三个方面进行细分。1、按城市细分例如:A:餐饮培训,当前…...
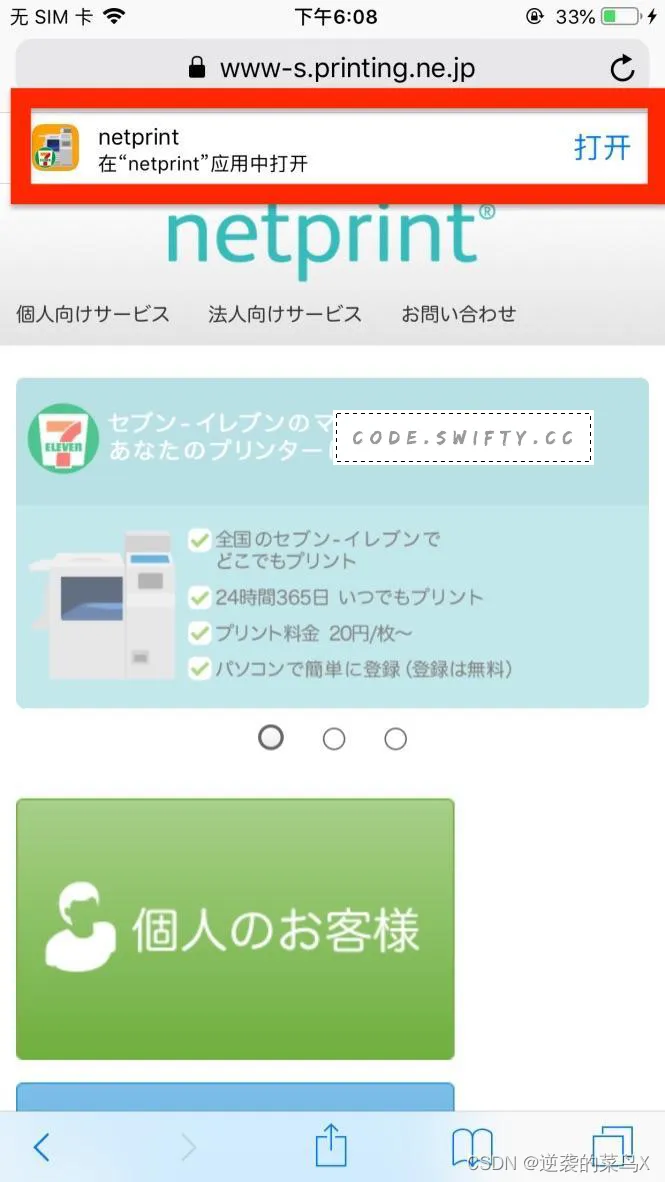
iOS创建Universal Link
iOS 9之前,一直使用的是URL Schemes技术来从外部对App进行跳转,但是iOS系统中进行URL Schemes跳转的时候如果没有安装App,会提示无法打开页面的提示。 iOS 9之后起可以使用Universal Links技术进行跳转页面,这是一种体验更加完美的…...

RuoYi-Vue搭建(若依)
项目简介 RuoYi-Vue基于SpringBootVue前后端分离的Java快速开发框架1.前端采用Vue、Element UI2.后端采用Spring Boot、Spring Security、Redis & Jwt3.权限认证使用Jwt,支持多终端认证系统4.支持加载动态权限菜单,多方式轻松权限控制5.高效率开发&a…...
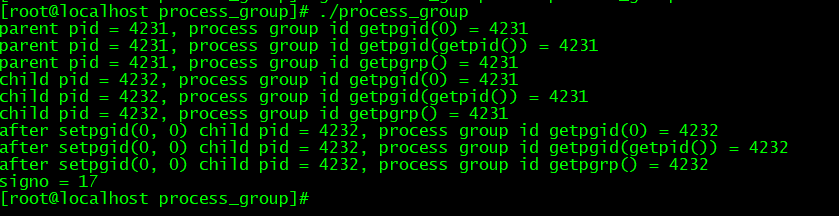
进程组和用处
进程组:一个或多个进程的集合,进程组id是一个正整数。组长进程:进程组id 进程id组长进程可以创建一个进程组,创建该进程组的进程,终止了,只要进程组有一个进程存在,进程组就存在,与…...

Nacos集群+Nginx负载均衡
搭建Nacos集群 注意: 3个或3个以上Nacos节点才能构成集群。要求服务器内存分配最好大于6G以上(如果不够则需修改nacos启动脚本中的默认内存配置)根据nacos自带的mysql建库脚本建立对应数据库(/conf/nacos-mysql.sql)如果是三台服…...

TypeScript 学习之类型兼容
TypeScript 的类型兼容性是基于结构子类型的。 结构类型是一种只使用其成员来描述类型的方式。 interface Named {name: string; }class Person {name: string; }let p: Named; p new Person();// 赋值成功,因为都是结构类型,只要Person 类型的包含 Nam…...

Linux软件管理RPM
目录 前言 RPM软件管理程序:rpm RPM默认安装的路径 PRM讲解前准备工作 RPM安装(install) RPM查询(query) RPM卸载(erase) RPM升级与更新(upgrade/freshen) RPM重…...

01背包问题
背包问题的递归解决过程如下: 第一步明确思路 在解决问题之前,为描述方便,首先定义一些变量:Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个…...
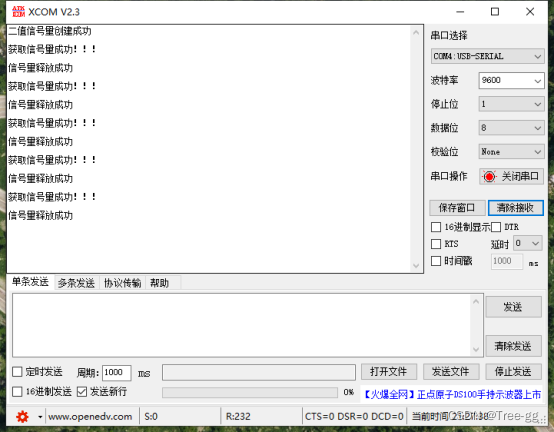
14_FreeRTOS二值信号量
目录 信号量的简介 队列与信号量的对比 二值信号量 二值信号量相关API函数 实验源码 信号量的简介 信号量是一种解决同步问题的机制,可以实现对共享资源的有序访问。 假设有一个人需要在停车场停车 1.首先判断停车场是否还有空车位(判断信号量是否有资源) 2.停车场正好…...

JavaScript随手笔记---轮播图(点击切换)
💌 所属专栏:【JavaScript随手笔记】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &#…...

机器人学 markdown数学公式常用语法
参考链接1 本文包含了markdown常用的数学公式,按照目录可查询选用 初始类 行内数学公式均用两个符号包裹行间数学公式均用两个符号包裹 行间数学公式均用两个符号包裹行间数学公式均用两个符号包裹,用于表示重要的、需在行间单独列出的公式 $行内数学…...

如何使用 Python 语言来编码和解码 JSON 对象
JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式,易于人阅读和编写。 JSON 函数 使用 JSON 函数需要导入 json 库:import json。 函数 描述 json.dumps 将 Python 对象编码成 JSON 字符串 json.loads 将已编码的 JSON 字符串解码为 Pyth…...

【蓝桥云课】求正整数的约数个数
一、求正整数n的约数个数 方法一(常用算法):从1到n逐一判断其能否整除n,若能整除n即为n的约数,否则不是n的约数。 方法二:从1到n\sqrt{n}n逐一判断是否为n的约数,当n\sqrt{n}n为n的约数时,个数加1&…...

刷题记录: wannafly25 E 牛客NC19469 01串 [线段树维护动态dp]
传送门:牛客 题目描述: Bieber拥有一个长度为n的01 串,他每次会选出这个串的一个子串作为曲谱唱歌,考虑该子串从左 往右读所组成的二进制数P。 Bieber每一秒歌唱可以让P增加或减少 2 的 k次方(k由Bieber选 定),但必须…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
