webrtc QOS笔记一 Neteq直方图算法浅读
webrtc QOS笔记一 Neteq直方图算法浅读
文章目录
- webrtc QOS笔记一 Neteq直方图算法浅读
- Histogram Algorithm
- 获取目标延迟
- 遗忘因子曲线
Histogram Algorithm
DelayManager::Update()->Histogram::Add() 会根据计算的iat_packet(inter arrival times, =实际包间间隔 / 打包时长),将该iat_packet插入IATVector直方图对应数组下标内。并更新该直方图的数据下标下概率参数。[M88 SRC]

一共有四步操作:
1、用遗忘因子,对历史数据的出现概率进行遗忘, 并统计概率合
buckets_[i]=buckets_[i]∗forget_factorbuckets\_[i] = buckets\_[i] * forget\_factorbuckets_[i]=buckets_[i]∗forget_factor
vector_sum=∑0buckets.size()buckets_[i]∗forget_factorvector\_sum=\sum_{0}^{buckets.size()} buckets\_[i] * forget\_factorvector_sum=∑0buckets.size()buckets_[i]∗forget_factor
2、增大本次计算到的IAT的概率值。
buckets_[value]=buckets_[value]+(1−forgetfactor_)buckets\_[value]=buckets\_[value]+(1−forget_factor\_)buckets_[value]=buckets_[value]+(1−forgetfactor_)
vector_sum=vector_sum+(1−forget_factor_)vector\_sum = vector\_sum + (1-forget\_factor\_)vector_sum=vector_sum+(1−forget_factor_)
- 例:
假如历史bucket 数据为:
buckets_ = {0,0,1,0}遗忘因子为 0.9:
forget_factor = 0.9新来的抖动延迟数据为66ms, 桶间为20ms一个单位, 那插入位置为 66 / 20 = 3,则更新后buckets = {0,0,0.9,0.1}假若使用%95分位的值作为目标延迟, 则更新后的目标延迟为 60ms.3、调整本次计算到的IAT的概率,使整个IAT的概率分布之和近似为1。调整方式为假设当前概率分布之和为tempSum,则:
vectorsum=1−vectorsumvector_sum=1−vector_sumvectorsum=1−vectorsum
buckets[n]={buckets_[n]−Min(∣vector_sum∣,buckets_[n]/16)if(vectorsum>0)buckets_[n]+Min(∣vector_sum∣,buckets_[n]/16)if(vectorsum>0)buckets_[n]= \begin{cases} buckets\_[n]−Min(∣vector\_sum∣,buckets\_[n]/16) if(vector_sum>0) \\ buckets\_[n]+Min(∣vector\_sum∣,buckets\_[n]/16) if(vector_sum>0) \\ \end{cases} buckets[n]={buckets_[n]−Min(∣vector_sum∣,buckets_[n]/16)if(vectorsum>0)buckets_[n]+Min(∣vector_sum∣,buckets_[n]/16)if(vectorsum>0)
4、更新forget_factor_, 使遗忘因子forget_factor_逼近base_forget_factor_
a.使用start_forget_weight_更新(默认初始值start_forget_weight_ = 2,base_forget_factor_=0.9993)
add_count_++add\_count\_++add_count_++
forget_factor_=1−(start_forget_weight_/(add_count_+1))forget\_factor\_=1−(start\_forget\_weight\_/(add\_count\_+1))forget_factor_=1−(start_forget_weight_/(add_count_+1))
forget_factor_=Max(0,Min(base_forget_factor_,forget_factor))forget\_factor\_=Max(0,Min(base\_forget\_factor\_,forget\_factor))forget_factor_=Max(0,Min(base_forget_factor_,forget_factor))
b. 其中的3是Q30的值,没有多大 = 0.000091552734375
forget_factor_=forgetfactor_+(base_forget_factor_−forget_factor_+3)/4forget\_factor\_=forget_factor\_+(base\_forget\_factor\_−forget\_factor\_+3)/4forget_factor_=forgetfactor_+(base_forget_factor_−forget_factor_+3)/4
获取目标延迟
依据probability获取此百分位的值作为目标延迟(初始值0.97)
∑0nbuckets_[n]>probability\sum_{0}^{n} buckets\_[n] > probability∑0nbuckets_[n]>probability
int Histogram::Quantile(int probability) {// Find the bucket for which the probability of observing an// inter-arrival time larger than or equal to |index| is larger than or// equal to |probability|. The sought probability is estimated using// the histogram as the reverse cumulant PDF, i.e., the sum of elements from// the end up until |index|. Now, since the sum of all elements is 1// (in Q30) by definition, and since the solution is often a low value for// |iat_index|, it is more efficient to start with |sum| = 1 and subtract// elements from the start of the histogram.int inverse_probability = (1 << 30) - probability;size_t index = 0; // Start from the beginning of |buckets_|.int sum = 1 << 30; // Assign to 1 in Q30.sum -= buckets_[index];while ((sum > inverse_probability) && (index < buckets_.size() - 1)) {// Subtract the probabilities one by one until the sum is no longer greater// than |inverse_probability|.++index;sum -= buckets_[index];}return static_cast<int>(index);
}
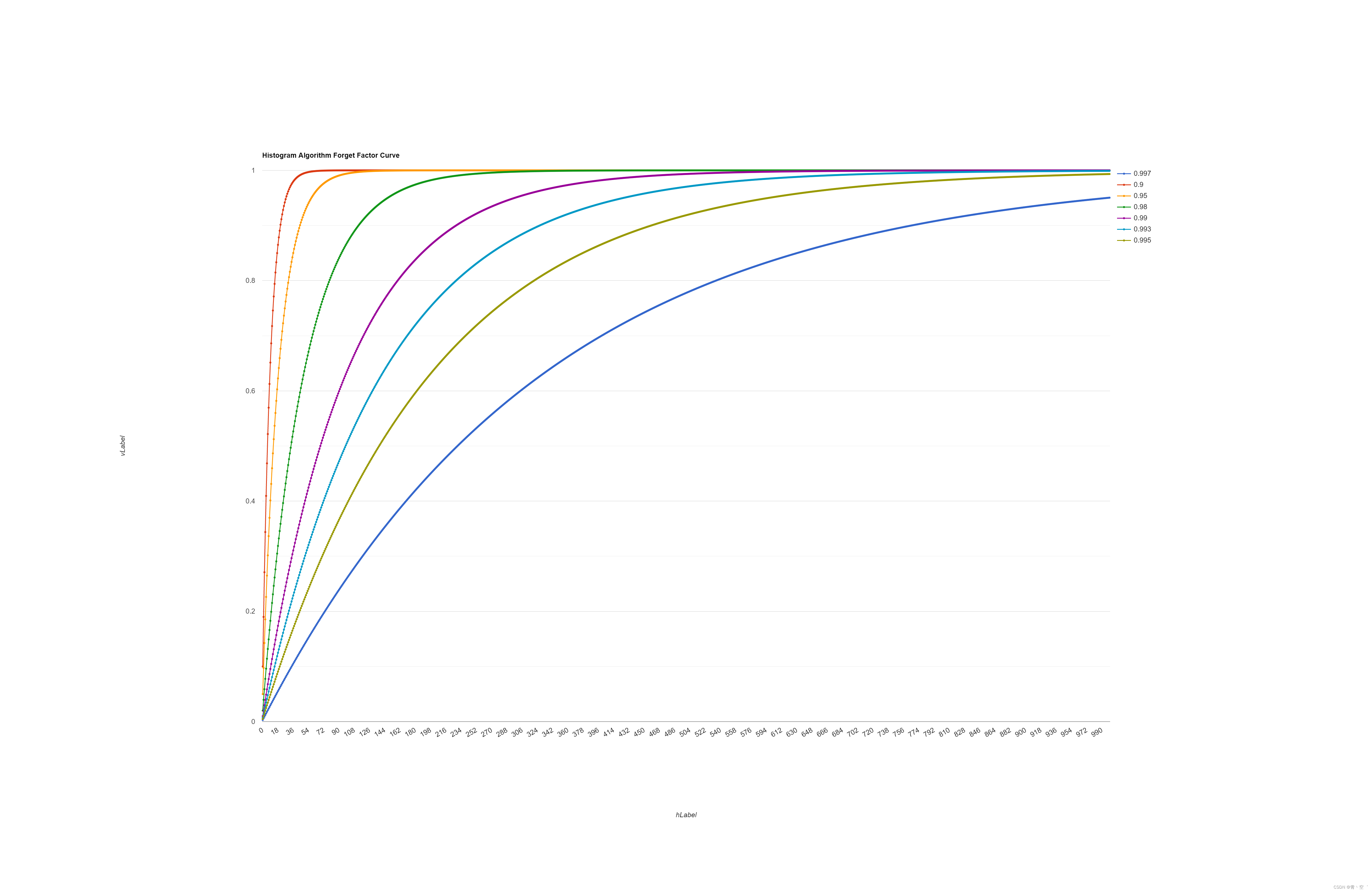
遗忘因子曲线
测试曲线,调整遗忘因子提高抖动估计灵敏度:
#include <iostream>
#include <cstdint>
#include <vector>uint32_t packet_loss_rate_ = 0;int main()
{std::vector<int> input;std::vector<float> buckets;float forget_factor = 0.9993;float val = 0;for (size_t k = 0; k < 1000; k ++) {val = val * forget_factor + (1-forget_factor);buckets.push_back(val);}for (int i = 0; i < 1000; ++i) {std::cout << buckets[i]<< " ";}return 0;
}
相关文章:

webrtc QOS笔记一 Neteq直方图算法浅读
webrtc QOS笔记一 Neteq直方图算法浅读 文章目录webrtc QOS笔记一 Neteq直方图算法浅读Histogram Algorithm获取目标延迟遗忘因子曲线Histogram Algorithm DelayManager::Update()->Histogram::Add() 会根据计算的iat_packet(inter arrival times, 实际包间间隔 / 打包时长…...

细分和切入点
本文重点介绍做SEO网站细分和切入点的方法:当我们的行业和关键词竞争性比较大的时候,我们可以考虑对行业或者产品做细分,从而找到切入点。可以按照以下三个方面进行细分。1、按城市细分例如:A:餐饮培训,当前…...
iOS创建Universal Link
iOS 9之前,一直使用的是URL Schemes技术来从外部对App进行跳转,但是iOS系统中进行URL Schemes跳转的时候如果没有安装App,会提示无法打开页面的提示。 iOS 9之后起可以使用Universal Links技术进行跳转页面,这是一种体验更加完美的…...

RuoYi-Vue搭建(若依)
项目简介 RuoYi-Vue基于SpringBootVue前后端分离的Java快速开发框架1.前端采用Vue、Element UI2.后端采用Spring Boot、Spring Security、Redis & Jwt3.权限认证使用Jwt,支持多终端认证系统4.支持加载动态权限菜单,多方式轻松权限控制5.高效率开发&a…...
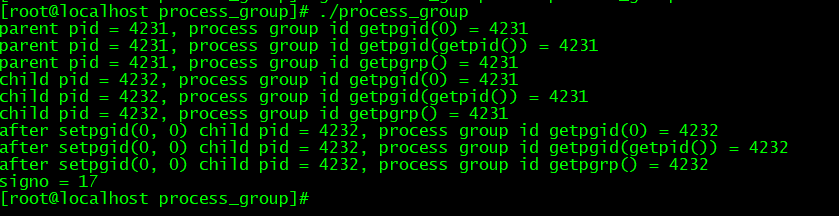
进程组和用处
进程组:一个或多个进程的集合,进程组id是一个正整数。组长进程:进程组id 进程id组长进程可以创建一个进程组,创建该进程组的进程,终止了,只要进程组有一个进程存在,进程组就存在,与…...

Nacos集群+Nginx负载均衡
搭建Nacos集群 注意: 3个或3个以上Nacos节点才能构成集群。要求服务器内存分配最好大于6G以上(如果不够则需修改nacos启动脚本中的默认内存配置)根据nacos自带的mysql建库脚本建立对应数据库(/conf/nacos-mysql.sql)如果是三台服…...

TypeScript 学习之类型兼容
TypeScript 的类型兼容性是基于结构子类型的。 结构类型是一种只使用其成员来描述类型的方式。 interface Named {name: string; }class Person {name: string; }let p: Named; p new Person();// 赋值成功,因为都是结构类型,只要Person 类型的包含 Nam…...

Linux软件管理RPM
目录 前言 RPM软件管理程序:rpm RPM默认安装的路径 PRM讲解前准备工作 RPM安装(install) RPM查询(query) RPM卸载(erase) RPM升级与更新(upgrade/freshen) RPM重…...

01背包问题
背包问题的递归解决过程如下: 第一步明确思路 在解决问题之前,为描述方便,首先定义一些变量:Vi表示第 i 个物品的价值,Wi表示第 i 个物品的体积,定义V(i,j):当前背包容量 j,前 i 个…...
14_FreeRTOS二值信号量
目录 信号量的简介 队列与信号量的对比 二值信号量 二值信号量相关API函数 实验源码 信号量的简介 信号量是一种解决同步问题的机制,可以实现对共享资源的有序访问。 假设有一个人需要在停车场停车 1.首先判断停车场是否还有空车位(判断信号量是否有资源) 2.停车场正好…...

JavaScript随手笔记---轮播图(点击切换)
💌 所属专栏:【JavaScript随手笔记】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &#…...

机器人学 markdown数学公式常用语法
参考链接1 本文包含了markdown常用的数学公式,按照目录可查询选用 初始类 行内数学公式均用两个符号包裹行间数学公式均用两个符号包裹 行间数学公式均用两个符号包裹行间数学公式均用两个符号包裹,用于表示重要的、需在行间单独列出的公式 $行内数学…...

如何使用 Python 语言来编码和解码 JSON 对象
JSON(JavaScript Object Notation) 是一种轻量级的数据交换格式,易于人阅读和编写。 JSON 函数 使用 JSON 函数需要导入 json 库:import json。 函数 描述 json.dumps 将 Python 对象编码成 JSON 字符串 json.loads 将已编码的 JSON 字符串解码为 Pyth…...

【蓝桥云课】求正整数的约数个数
一、求正整数n的约数个数 方法一(常用算法):从1到n逐一判断其能否整除n,若能整除n即为n的约数,否则不是n的约数。 方法二:从1到n\sqrt{n}n逐一判断是否为n的约数,当n\sqrt{n}n为n的约数时,个数加1&…...

刷题记录: wannafly25 E 牛客NC19469 01串 [线段树维护动态dp]
传送门:牛客 题目描述: Bieber拥有一个长度为n的01 串,他每次会选出这个串的一个子串作为曲谱唱歌,考虑该子串从左 往右读所组成的二进制数P。 Bieber每一秒歌唱可以让P增加或减少 2 的 k次方(k由Bieber选 定),但必须…...
懂九转大肠的微软New Bing 内测申请教程
最近微软的New Bing开放内测了,网上已经有拿到内测资格的大佬们对比了ChatGPT和New Bing。对比结果是New Bing比ChatGPT更强大。来看看具体对比例子吧 1.时效性更强 ChatGPT的库比较老,跟不上时事,比如你问它九转大肠的梗,ChatG…...

WRAN翻译
基于小波的图像超分辨残差注意力网络 Wavelet-based residual attention network for image super-resolution 代码: https://github.com/xueshengke/WRANSR-keras 摘要: 图像超分辨率技术是图像处理和计算机视觉领域的一项基础技术。近年来,…...

ROS学习笔记——第二章 ROS通信机制
主要跟着[1]学习ros::Rate r(1); //错误,应改为ros::Rate r(10);[2]对Topic通信打的比方很形象,便于理解记忆。[3]有整个过程的图片,对于初学者更加友好[4]对发布者的代码注释非常好,方便进一步学习此外CMake官方文档可以查询相关…...
MacOS Pytorch 机器学习环境搭建
学习 Pytorch ,首先要搭建好环境,这里将采用 Anoconda Pytorch PyCharm 来一起构建 Pytorch 学习环境。 1. Anoconda 安装与环境创建 Anoconda 官方介绍:提供了在一台机器上执行 Python/R 数据科学和机器学习的最简单方法。 为什么最简单…...

项目——博客系统
文章目录项目优点项目创建创建相应的目录,文件,表,导入前端资源实现common工具类实现拦截器验证用户登录实现统一数据返回格式实现加盐加密类实现encrypt方法实现decrypt方法实现SessionUtil类实现注册页面实现前端代码实现后端代码实现登录页…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

spring boot使用HttpServletResponse实现sse后端流式输出消息
1.以前只是看过SSE的相关文章,没有具体实践,这次接入AI大模型使用到了流式输出,涉及到给前端流式返回,所以记录一下。 2.resp要设置为text/event-stream resp.setContentType("text/event-stream"); resp.setCharacter…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...
