排序算法 - 快速排序(4种方法实现)
快速排序
- 快速排序是啥?
- 三数取中:
- 1.挖坑法(推荐掌握)
- 2.前后指针法(推荐掌握)
- 3.左右指针法(霍尔版本)(容易出错)
- 4.非递归实现
本篇文章的源代码在这,需要自取:Gitee
快速排序是啥?
快速排序是一种常见的排序算法,其基本原理是分治和递归。它的基本思路是,在数组中选择一个元素作为基准值,然后将数组中小于基准值的元素移动到它的左边,大于基准值的元素移动到它的右边。然后对左右两个子数组递归地重复这个过程,直到子数组的大小为1或0。
在实现快速排序时,可以使用 三数取中法来选取基准值和分区,这样可以有效避免最坏情况的发生。
三数取中法:从待排序区间的首、中、尾三个位置上的数选取一个中间值作为基准值。
三数取中:
//三数取中
int GetMidIndex(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] < a[right]){return right;}elsereturn left;}else//a[left] > a[mid]{if (a[mid] > a[right]){return mid;}else if(a[left] > a[right]){return right;}else{return left;}}
}
GetMidIndex 函数接受一个整型数组 a,以及要选择基准元素的左右边界索引 left 和 right。函数首先计算出中间索引 mid,通过 (left + right) / 2 的方式获得。
然后,函数根据数组中三个元素 a[left]、a[mid] 和 a[right] 的值进行比较,以确定基准元素的索引。
如果 a[left] 小于 a[mid],则继续比较 a[mid] 和 a[right]。如果 a[mid] 小于 a[right],说明 a[mid] 是中间的元素,其值介于 a[left] 和 a[right] 之间,因此将 mid 作为基准元素的索引返回。
如果 a[mid] 不小于 a[right],则根据 a[left] 和 a[right] 的大小关系来选择基准元素的索引。如果 a[left] 小于 a[right],说明 a[left] 是中间的元素,其值介于 a[mid] 和 a[right] 之间,因此将 right 作为基准元素的索引返回。否则,如果 a[left] 大于等于 a[right],说明 a[right] 是中间的元素,其值介于 a[left] 和 a[mid] 之间,因此将 left 作为基准元素的索引返回。
如果 a[left] 大于 a[mid],则继续比较 a[mid] 和 a[right]。如果 a[mid] 大于 a[right],说明 a[mid] 是中间的元素,其值介于 a[left] 和 a[right] 之间,因此将 mid 作为基准元素的索引返回。
如果 a[mid] 不大于 a[right],则根据 a[left] 和 a[right] 的大小关系来选择基准元素的索引。如果 a[left] 大于 a[right],说明 a[left] 是中间的元素,其值介于 a[right] 和 a[mid] 之间,因此将 right 作为基准元素的索引返回。否则,如果 a[left] 小于等于 a[right],说明 a[left] 是中间的元素,其值介于 a[mid] 和 a[right] 之间,因此将 left 作为基准元素的索引返回。
通过使用三数取中法选择基准元素,可以在大多数情况下选取到接近中间值的元素,提高快速排序的效率和性能,并减少最坏情况的发生
1.挖坑法(推荐掌握)
以下是挖坑法的详细过程:
- 选择一个值基准值(在这用三数取中)。通常情况下,选择数组中第一个元素作为基准值。
- 将数组中小于基准值的元素移动到它的左边,大于基准值的元素移动到它的右边。(左边找大,右边找小)。
- 对左右两个子数组递归地重复上述过程,直到子数组的大小为1或0。
- 合并子数组,得到排序后的数组。

//挖坑法
int PartSort2(int* a, int left, int right)
{//三数取中int midi = GetMidIndex(a, left, right);Swap(&a[midi], &a[left]);//把中间值放到left位置int keyi = left;while (left < right){while (left < right && a[right] >= a[keyi]){right--;}Swap(&a[keyi], &a[right]);keyi = right;while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[keyi], &a[left]);keyi = left;}return keyi;
}//快排
void QuickSort(int* a, int left,int right)
{if (left >= right){return ;}int keyi = PartSort2(a, left, right);//[left,keyi-1][keyi][keyi+1,right]QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}
- PartSort2 函数是挖坑法的核心实现。它接受一个整型数组 a,以及要排序的左右边界索引 left 和 right。函数首先选择一个中间索引 midi,并将 a[midi] 与 a[left] 进行交换,将 a[left] 作为基准元素。
- 然后,函数使用两个指针 left 和 right 在数组中进行扫描。从右边开始,当 a[right] 大于等于基准元素 a[keyi] 时,将 right 指针左移,直到找到小于基准元素的元素为止。
- 然后,将该元素与 a[keyi] 进行交换,将 keyi 更新为 right。
- 接下来,从左边开始,当 a[left] 小于等于基准元素 a[keyi] 时,将 left 指针右移,直到找到大于基准元素的元素为止。
- 然后,将该元素与 a[keyi] 进行交换,将 keyi 更新为 left。
- 重复这个过程直到 left 和 right 指针相遇,然后返回 keyi,该索引将数组分为两部分:左边的元素小于等于基准元素,右边的元素大于等于基准元素。
QuickSort 函数接受一个整型数组 a,以及要排序的左右边界索引 left 和 right。首先,它检查是否满足递归终止条件,即 left >= right,如果满足条件,则直接返回。否则,它调用PartSort2 函数获取基准元素的索引 keyi,然后将数组分为三部分:[left, keyi-1]、[keyi] 和 [keyi+1, right]。接着,它递归调用 QuickSort 函数对左边和右边的子数组进行排序。
2.前后指针法(推荐掌握)

//前后指针法
int PartSort3(int* a, int left, int right)
{int midi = GetMidIndex(a, left, right);Swap(&a[midi], &a[left]);//end找小,如果 a[end]<a[keyi],++begin(这时begin位置的值一定比keyi位置值大),再交换begin和end的位置 int keyi = left;int begin = left;int end = left+1;while (end <=right){if (a[end] < a[keyi] ){++begin;Swap(&a[begin], &a[end]);}++end;}Swap(&a[begin], &a[keyi]);return begin;
}//快排
void QuickSort(int* a, int left,int right)
{if (left >= right){return ;}int keyi = PartSort3(a, left, right);//[left,keyi-1][keyi][keyi+1,right]QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);
}
- PartSort3 函数使用了前后指针法(双指针法)进行数组分区。函数接受一个整型数组 a,以及要分区的左右边界索引 left 和 right。
- 首先,函数调用 GetMidIndex 函数获取基准元素的索引 midi,然后将 a[midi] 和 a[left] 进行交换,将 a[left] 设置为基准元素。
- 接下来,函数初始化两个指针 begin 和 end,分别从 left 和 left + 1 开始遍历数组。
- 在遍历过程中,end 指针向右移动,扫描数组元素。当 a[end] 小于基准元素 a[keyi] 时,将 begin 指针右移一位,并交换 a[begin] 和 a[end] 的值。这样,较小的元素就会被移动到 begin 的位置,而 begin 之前的元素都小于基准元素。
- 最后,将基准元素 a[keyi] 移动到合适的位置,即将其与 a[begin] 交换。此时,数组被分为两部分:左边的元素小于基准元素,右边的元素大于等于基准元素。
- 最后,函数返回基准元素的索引 begin。
QuickSort函数作用同上
3.左右指针法(霍尔版本)(容易出错)
快速排序的左右指针法(双指针法)是一种常见的实现方式,它利用两个指针从数组的两端开始,逐步向中间移动,并进行元素的比较和交换,以实现数组的分区和排序。
其基本思想如下:
-
选择一个基准元素(通常是数组的第一个元素)。
-
使用两个指针,一个从左边开始(一般称为左指针),一个从右边开始(一般称为右指针)。
-
左指针从左边开始向右移动,直到找到一个大于基准元素的元素。
-
右指针从右边开始向左移动,直到找到一个小于基准元素的元素。
-
如果左指针的位置小于右指针的位置,则交换左指针和右指针所指向的元素。
-
重复步骤 3-5,直到左指针和右指针相遇。
-
将基准元素与左指针所指向的元素进行交换,此时基准元素的位置已经确定。
-
根据基准元素的位置,将数组分成两部分,左边的元素都小于基准元素,右边的元素都大于基准元素。
-
对基准元素左右两部分的子数组分别重复以上步骤,直到所有的子数组都有序。
//左右指针(霍尔版本)(容易出错)
int PartSort1(int* a, int left,int right)
{int midi = GetMidIndex(a, left, right);Swap(&a[midi], &a[left]);int keyi = left;while (left < right){while (left < right && a[keyi]<=a[right]){right--;}while (left < right && a[keyi]>=a[left]){left++;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}//快排void QuickSort(int* a, int left,int right){if (left >= right){return ;}int keyi = PartSort1(a, left, right);//[left,keyi-1][keyi][keyi+1,right]QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
- PartSort1 函数使用左右指针法(霍尔版本)进行数组分区。函数接受一个整型数组 a,以及要分区的左右边界索引 left 和 right。
- 首先,函数调用 GetMidIndex 函数获取基准元素的索引 midi,然后将 a[midi] 和 a[left] 进行交换,将 a[left] 设置为基准元素。
- 接下来,函数使用两个指针 left 和 right 分别从数组的左右两端开始遍历。
- 在遍历过程中,首先从右边开始,找到第一个小于基准元素的元素,将 right 指针左移一位,直到找到小于基准元素的元素或 left 和 right 指针相遇。
- 然后,从左边开始,找到第一个大于基准元素的元素,将 left 指针右移一位,直到找到大于基准元素的元素或 left 和 right 指针相遇。
- 如果 left 小于 right,则交换 a[left] 和 a[right],将小于基准元素的元素移动到左侧,大于基准元素的元素移动到右侧。
- 重复上述步骤,直到 left 和 right 指针相遇,此时完成了一次分区。将基准元素 a[keyi] 移动到合适的位置,即将其与 a[left] 交换。
- 最后,函数返回基准元素的索引 left。
QuickSort函数同上
4.非递归实现
-
非递归的快速排序使用栈来存储待处理的子数组的起始和结束位置。初始时,将整个数组的起始和结束位置压入栈中。
-
然后,进入循环,从栈中弹出一个子数组,对其进行分区操作,得到基准元素的位置。根据分区的结果,将子数组划分为两个部分:一个部分是基准元素左边的子数组,另一个部分是基准元素右边的子数组。
-
接下来,将需要进一步处理的子数组的起始和结束位置压入栈中。这样,栈中存储的就是待处理的子数组。
-
重复以上步骤,直到栈为空。这意味着所有的子数组都已经被处理完毕,排序完成。
-
通过使用栈来模拟递归调用过程,非递归的快速排序能够有效地对数组进行分区和排序,同时避免了递归带来的函数调用开销。这种实现方式通常具有较好的性能和效率,特别适用于处理大规模的数据集。
void QuickSortNonR(int* a, int begin, int end)
{ST st;StackInit(&st);StackPush(&st, end);StackPush(&st,begin);while (!StackEmpty(&st)){int left = StackTop(&st);StackPop(&st);int right = StackTop(&st);StackPop(&st);int keyi = PartSort2(a, left, right);//[left,keyi-1][keyi][keyi+1,right]if(keyi+1<right){StackPush(&st, right);StackPush(&st, keyi + 1);}if (left < keyi-1){StackPush(&st, keyi - 1);StackPush(&st, left);}}StackDestory(&st);
}
- QuickSortNonR 函数实现了非递归版本的快速排序。它接受一个整型数组 a,以及要排序的起始位置 begin 和结束位置 end。
- 首先,函数创建一个栈 st,用于存储待处理的子数组的起始和结束位置。将 end 和 begin 分别压入栈中,表示对整个数组进行排序。
- 进入循环,只要栈不为空,就执行以下操作:
- 从栈中弹出两个元素,分别赋值给 left 和 right,表示当前要处理的子数组的起始和结束位置。
- 调用 PartSort2 函数对子数组进行分区,得到基准元素的位置 keyi。
- 根据分区的结果,将子数组划分为 [left, keyi-1]、[keyi]、[keyi+1, right] 三个部分。
- 如果 keyi + 1 < right,说明右侧子数组仍然有元素需要排序,将右侧子数组的起始位置 keyi + 1 和结束位置 right 压入栈中。
- 如果 left < keyi - 1,说明左侧子数组仍然有元素需要排序,将左侧子数组的起始位置 left 和结束位置 keyi - 1 压入栈中。
- 循环继续进行,直到栈为空,表示所有子数组都被处理完毕。
- 最后,销毁栈 st,完成非递归版本的快速排序。
相关文章:

排序算法 - 快速排序(4种方法实现)
快速排序 快速排序是啥?三数取中:1.挖坑法(推荐掌握)2.前后指针法(推荐掌握)3.左右指针法(霍尔版本)(容易出错)4.非递归实现 本篇文章的源代码在这࿰…...
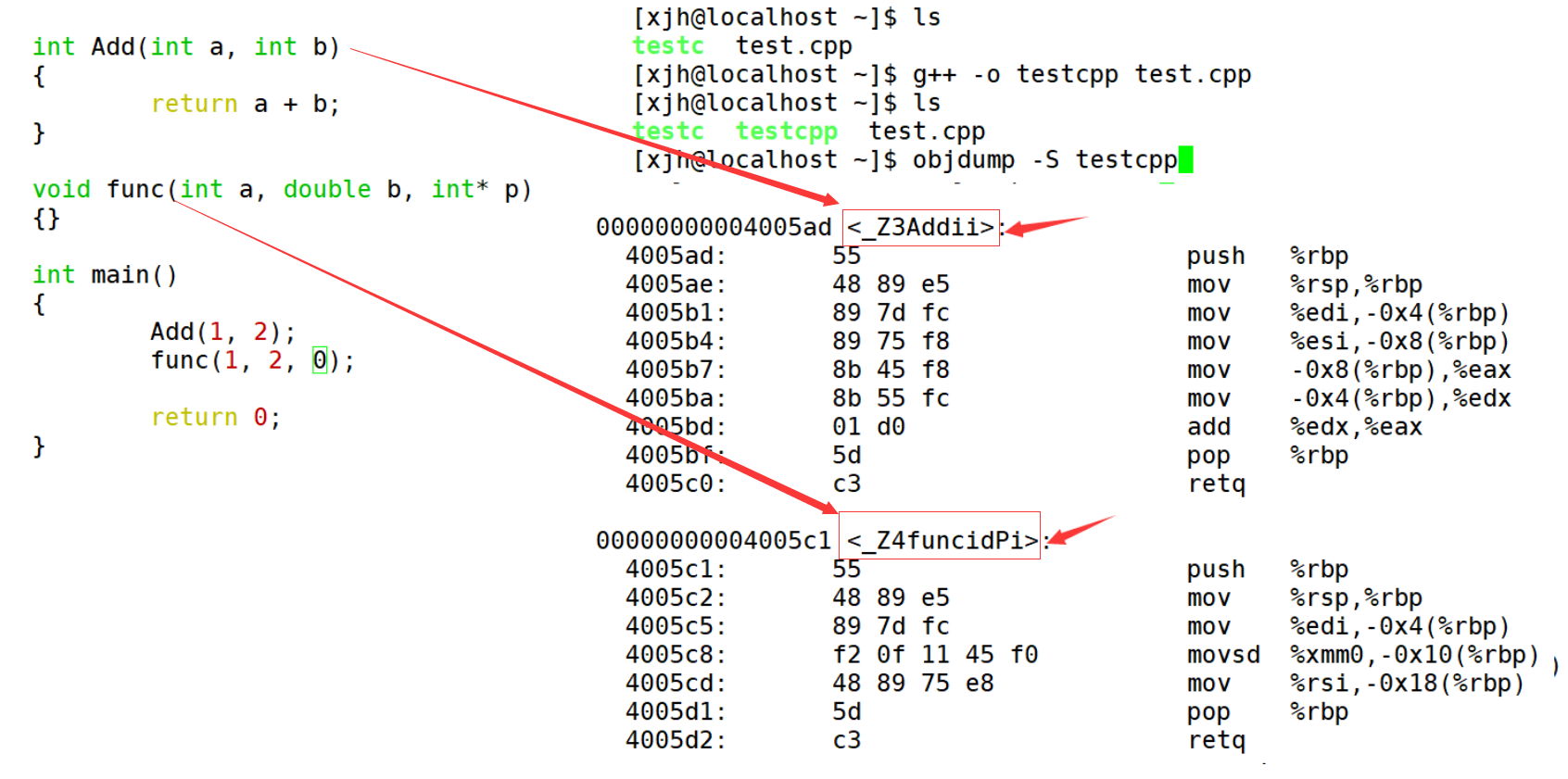
C++入门知识点
目录 命名空间 命名空间定义 命名空间使用 法一:加命名空间名称及作用域限定符:: 法二:使用using部分展开(授权)某个命名空间中的成员 法三:使用using对整个命名空间全部展开(授权…...

开眼界了,AI绘画商业化最强玩家是“淘宝商家”
图片来源:由无界AI生成 7月,2023世界人工智能大会在上海召开,顶尖的投资人、创业者都去了。 创业者吐槽:投我啊,我很强。 投资人反问:你的商业模式是什么?护城河是什么? 创业者投资人…...
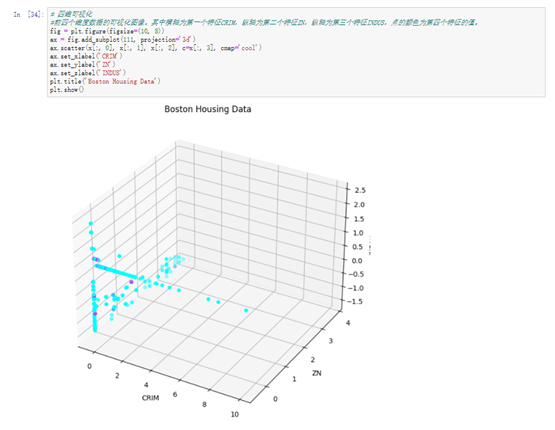
机器学习与深度学习——自定义函数进行线性回归模型
机器学习与深度学习——自定义函数进行线性回归模型 目的与要求 1、通过自定义函数进行线性回归模型对boston数据集前两个维度的数据进行模型训练并画出SSE和Epoch曲线图,画出真实值和预测值的散点图,最后进行二维和三维度可视化展示数据区域。 2、通过…...

大屏项目也不难
项目环境搭建 使用create-vue初始化项目 npm init vuelatest准备utils模块 业务背景:大屏项目属于后台项目的一个子项目,用户的token是共享的 后台项目 - token - cookie 大屏项目要以同样的方式把token获取到,然后拼接到axios的请求头中…...

c#webclient请求中经常出现的几种异常
WebClient是.NET Framework提供的用于HTTP请求的类,如果在使用WebClient时遇到异常,我们可以根据具体的异常类型进行处理。 以下是一些常见的WebClient异常及其处理方法: System.Net.WebException WebException通常是由于请求超时、网络连…...
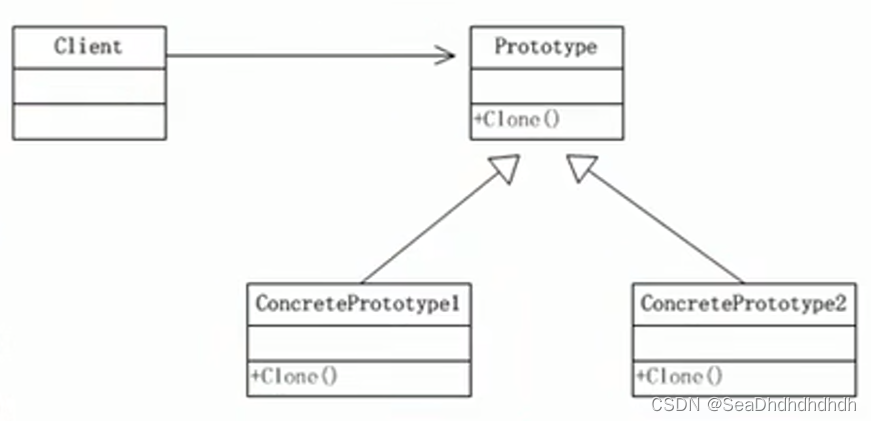
设计模式-原型模式
目录 一、传统方式 二、原型模式 三、浅拷贝和深拷贝 克隆羊问题: 现在有一只羊tom,姓名为: tom,年龄为: 1,颜色为: 白色,请编写程序创建和tom羊属性完全相同的10只羊。 一、传统方式 public class Client {public static vo…...

sentinel介绍-分布式微服务流量控制
官网地址 https://sentinelguard.io/ 介绍 随着微服务的流行,服务和服务之间的稳定性变得越来越重要。Sentinel 是面向分布式、多语言异构化服务架构的流量治理组件,主要以流量为切入点,从流量路由、流量控制、流量整形、熔断降级、系统自…...

基于Redisson的Redis结合布隆过滤器使用
一、场景 缓存穿透问题 一般情况下,先查询Redis缓存,如果Redis中没有,再查询MySQL。当某一时刻访问redis的大量key都在redis中不存在时,所有查询都要访问数据库,造成数据库压力顿时上升,这就是缓存穿透。…...

BrowserRouter刷新404解决方案
1、本地开发环境 在js脚本命令里加上 --history-api-fallback "scripts": {"serve": "webpack serve --config webpack.dev.js --history-api-fallback" }2、生产环境,可以修改 nglnx 配置: server {listen XXXX; //端口号…...
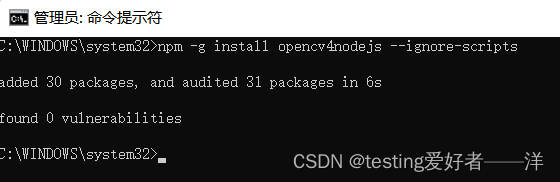
解决appium-doctor报opencv4nodejs cannot be found
一、下载cmake 在CMake官网下载:cmake-3.6.1-win64-x64.msi 二、安装cmake cmake安装过程 在安装时要选择勾选为所有用户添加CMake环境变量 三、检查cmake安装 重新管理员打开dos系统cmd命令提示符,输入cmake -version cmake -version四、安装opencv4no…...

安卓通过adb pull和adb push 手机与电脑之间传输文件
1.可以参考这篇文章 https://www.cnblogs.com/hhddcpp/p/4247923.html2.根据上面的文章,我做了如下修改 //设置/system为可读写: adb remount //复制手机中的文件到电脑中。需要在电脑中新建一个文件夹,我新建的文件夹为ce文件夹 adb pull …...

java常用的lambda表达式总结
一、概述 lambda表达式是JDK8中的一个新特性,对某些匿名内部类进行简化,是函数式编程; 二、基本格式 (参数列表)->{方法体代码} 三、Stream流 是jdk8中的新特性,将数据以流的形式进行操作 三、常用方法解析 3.1、准备工作 …...
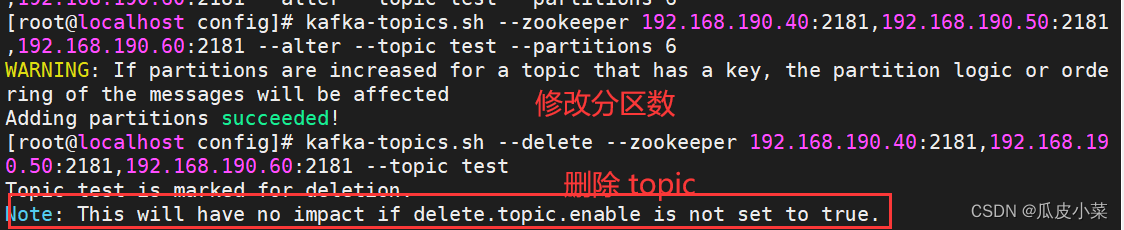
分布式应用之zookeeper集群+消息队列Kafka
一、zookeeper集群的相关知识 1.zookeeper的概念 ZooKeeper是一个分布式的,开放源码的分布式应用程序协调服务,是Google的Chubby一个开源的实现,是Hadoop和Hbase的重要组件。它是一个为分布式应用提供一致性服务的软件,提供的功能…...
)
GStreamer学习笔记(四)
Time management 仅当管道处于PLAYING状态时,可以刷新屏幕。如果不在PLAYING状态,什么都不做,因为大多数查询都会失败。 函数与知识点 GstClockTime 说明:所需的超时时间必须以GstClockTime的形式指定。即以纳秒(ns…...
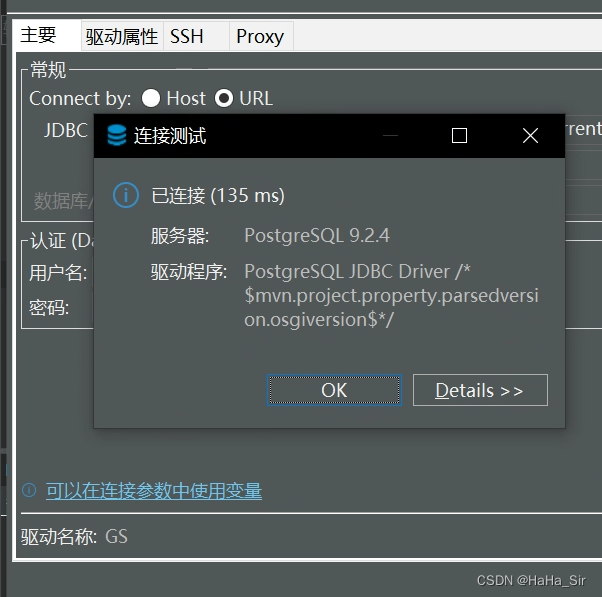
DBeaver连接华为高斯数据库 DBeaver连接Gaussdb数据库 DBeaver connect Gaussdb
DBeaver连接华为高斯数据库 DBeaver连接Gaussdb数据库 DBeaver connect Gaussdb 一、概述 华为GaussDB出来已经有一段时间,最近工作中刚到Gauss数据库。作为coder,那么如何通过可视化工具来操作Gauss呢? 本文将记录使用免费、开源的DBeaver来…...

.net core 2.1 简单部署IIS运行
netcore的项目不像netFramework那么方便部署到iis还是要费点功夫的 比如我想把这个netcore2.1的项目部署到iis并运行: 按照步骤走: 一、确认自己的netcore环境 1、需要安装下面3个环境包(如果电脑已安装请忽略) 检查是否安装cmd命令:cmd&…...

提高视觉检测系统稳定性的隐藏办法——10G高速图像采集卡
提高视觉检测系统稳定性的隐藏办法——10G高速图像采集卡 目前,随着我国各方面配套基础设施建设的完善,企业技术、资金的积累,各行各业积极探索和大胆的尝试机器视觉技术,实现工业自动化、智能化。在机器视觉系统的使用过程中&am…...

注解方式实现数据库字段加密与解密
目录 前言实现步骤定义注解加密工具类定义mybatis拦截器 总结 前言 一些敏感信息存入数据需要进行加密处理,比如电话号码,身份证号码等,从数据库取出到前端展示时需要解密,如果分别在存入取出时去做处理,会很繁锁&…...
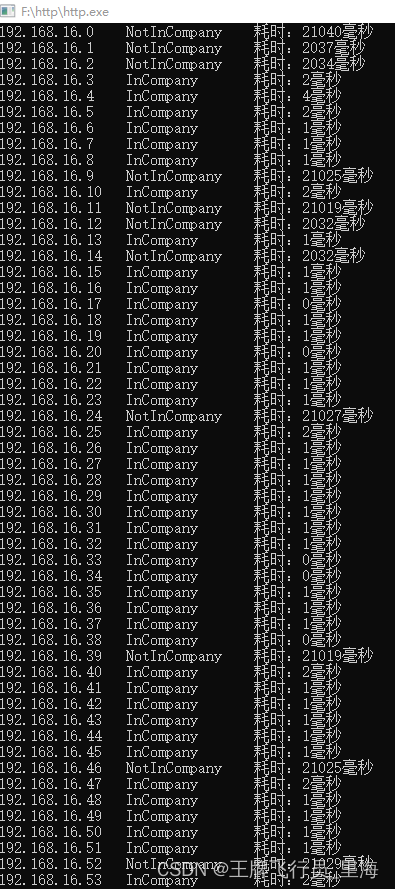
C\C++ 使用socket判断ip是否能连通
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan 简介: 使用socket判断ip是否能联通 效果: 代码: #include <iostream> #include <cstdlib> #include <cstdio> #include &…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
