一本通1919:【02NOIP普及组】选数
这道题感觉很好玩。
正文:
先放题目:
信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn)![]() http://ybt.ssoier.cn:8088/problem_show.php?pid=1919
http://ybt.ssoier.cn:8088/problem_show.php?pid=1919
描述
已知 n 个整数 x1,x2,…,xn,以及一个整数 k(k<n)。从 n 个整数中任选 k 个整数相加,可分别得到一系列的和。例如当 n=4,k=3,4 个整数分别为 3,7,12,19 时,可得全部的组合与它们的和为:
3+7+12=22 3+7+19=29 7+12+19=38 3+12+19=34。
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:(3+7+19=29)
输入
键盘输入,格式为:
n , k (1<=n<=20,k<n)
x1,x2,…,xn (1<=xi<=5000000)
输出
屏幕输出,格式为:
一个整数(满足条件的种数)。
输入样例
4 3
3 7 12 19输出样例
1看到这道题第一感就是和另一道题特别特别特别像,大家可以看看
信息学奥赛一本通(C++版)在线评测系统 (ssoier.cn)![]() http://ybt.ssoier.cn:8088/problem_show.php?pid=1317
http://ybt.ssoier.cn:8088/problem_show.php?pid=1317
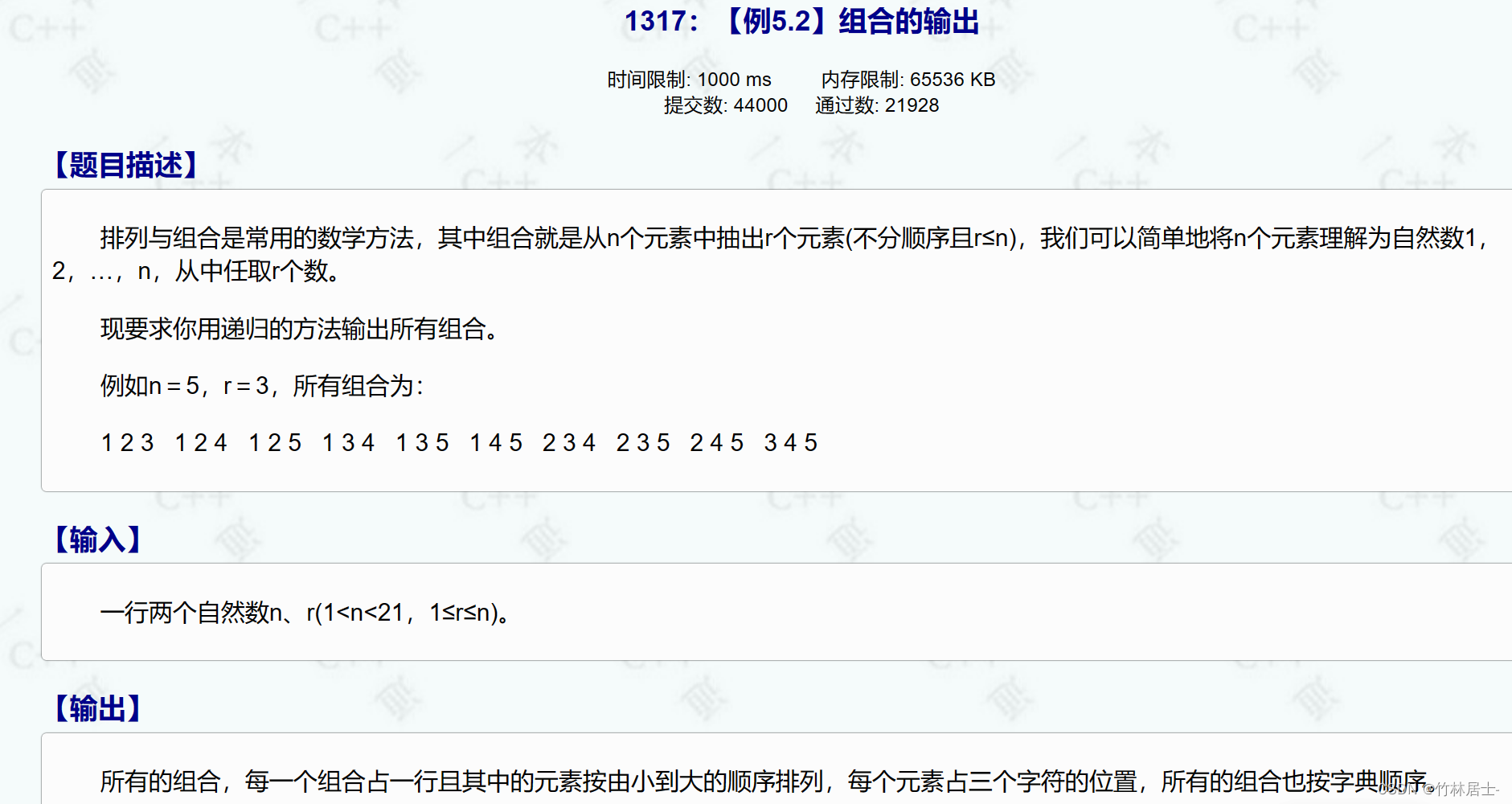
其实就是把求出的排列不输出,求出来哪些是质数就行了。
思路:
用深度优先搜索(dfs)求出所有的组合,最后求解即可。
代码:
判断质数
void isprime(int x)
{for(int i=2;i<=sqrt(x);i++){if(x%i==0) return;}res++;
}搜索
//基本上和组合的输出没什么区别,只是把输出的地方改成判断质数
void dfs(int step,int pre)
{y=0;if(step>=k){for(int i=0;i<k;i++) y+=x[i];isprime(y);return;}for(int i=pre+1;i<=n;i++){x[step]=a[i];dfs(step+1,i);}
}主函数
int main()
{scanf("%d%d",&n,&k);for(int i=1;i<=n;i++)scanf("%d",&a[i]);dfs(0,0);printf("%d",res);return 0;
}完整的代码
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<stack>
#include<queue>
using namespace std;const int N=25;
int res,n,k,a[N],x[N],y;void isprime(int x)
{for(int i=2;i<=sqrt(x);i++){if(x%i==0) return;}res++;
}
void dfs(int step,int pre)
{y=0;if(step>=k){for(int i=0;i<k;i++) y+=x[i];isprime(y);return;}for(int i=pre+1;i<=n;i++){x[step]=a[i];dfs(step+1,i);}
}int main()
{scanf("%d%d",&n,&k);for(int i=1;i<=n;i++)scanf("%d",&a[i]);dfs(0,0);printf("%d",res);return 0;
} 没登陆的复制链接
云剪贴板 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)![]() https://www.luogu.com.cn/paste/ih8rpwlt
https://www.luogu.com.cn/paste/ih8rpwlt
相关文章:
一本通1919:【02NOIP普及组】选数
这道题感觉很好玩。 正文: 先放题目: 信息学奥赛一本通(C版)在线评测系统 (ssoier.cn)http://ybt.ssoier.cn:8088/problem_show.php?pid1919 描述 已知 n 个整数 x1,x2,…,xn,以及一个整数 k(k&#…...

Kubernetes 集群管理和编排
文章目录 总纲第一章:引入 Kubernetes什么是容器编排和管理?容器编排和管理的重要性Kubernetes作为容器编排和管理解决方案 Kubernetes 的背景和发展起源和发展历程Kubernetes 项目的目标和动机 Kubernetes 的作用和优势作用优势 Kubernetes 的特点和核心…...

DDS协议--[第六章][Discovery]
DDS协议–Discovery 文章目录 DDS协议--Discovery侦听通告DDS提供发现协议参与者发现阶段(PDP)端点发现阶段(EDP)Fast DDS提供如下四种发现机制:简单发现机制简单发现机制步骤:侦听 侦听定位器用于接收DomainParticipant上的传入流量,是DDS发现机制和数据传输机制的关键…...

如何设置iptables,让网络流量转发给内部容器mysql
1.创建一个mysql ,无法外部访问 docker run -d --name mysql_container -e MYSQL_ROOT_PASSWORDliuyunshengsir -v /path/to/mysql_data:/var/lib/mysql mysql2.设置规则外部直接可访问 要使用 iptables 将网络流量转发给内部容器中的 MySQL 服务,你可…...
数字IC实践项目(7)—CNN加速器的设计和实现(付费项目)
数字IC实践项目(7)—基于Verilog的CNN加速器(付费项目) 写在前面的话项目整体框图神经网络框图完整电路框图 项目简介和学习目的软件环境要求 资源占用&板载功耗总结 写在前面的话 项目介绍: 卷积神经网络硬件加速…...

基于深度学习的高精度80类动物目标检测系统(PyTorch+Pyside6+YOLOv5模型)
摘要:基于深度学习的高精度80类动物目标检测识别系统可用于日常生活中或野外来检测与定位80类动物目标,利用深度学习算法可实现图片、视频、摄像头等方式的80类动物目标检测识别,另外支持结果可视化与图片或视频检测结果的导出。本系统采用YO…...

海康摄像头开发笔记(一):连接防爆摄像头、配置摄像头网段、设置rtsp码流、播放rtsp流、获取rtsp流、调优rtsp流播放延迟以及录像存储
文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/131679108 红胖子(红模仿)的博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬结…...

【NCNN】NCNN中Mat与CV中Mat的使用区别及相互转换方法
目录 相同点与不同点cv::Mat转ncnn::Matcv::Mat CV_8UC3 -> ncnn::Mat 3 channel swap RGB/BGRcv::Mat CV_8UC3 -> ncnn::Mat 1 channel do RGB2GRAY/BGR2GRAYcv::Mat CV_8UC1 -> ncnn::Mat 1 channel ncnn::Mat转cv::Mancnn::Mat 3 channel -> cv::Mat CV_8UC3 …...

Android 13 设置自动进入wifi adb模式
Android 13 设置自动进入wifi adb模式 文章目录 Android 13 设置自动进入wifi adb模式一、前言:二、解决Android 13 wifi adb每次重启自动重置问题方法1、分析系统中每次重置wifi adb属性的代码2、在开机广播里面进行设置wifi adb 相关属性(1)…...
插入排序)
(笔记)插入排序
插入排序 插入排序是一种简单且常见的排序算法,它通过重复将一个元素插入到已经排好序的一组元素中,来达到排序的目的。在插入排序算法中,将待排序序列分为已排序和未排序两个部分。初始时,已排序部分只包含一个记录,…...
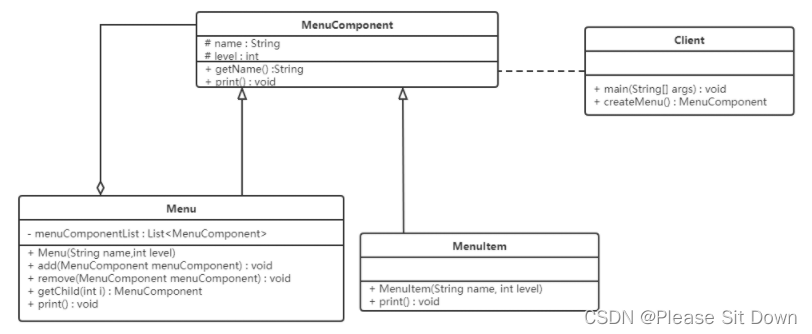
结构型模式 - 组合模式
概述 对于这个图片肯定会非常熟悉,上图我们可以看做是一个文件系统,对于这样的结构我们称之为树形结构。在树形结构中可以通过调用某个方法来遍历整个树,当我们找到某个叶子节点后,就可以对叶子节点进行相关的操作。可以将这颗树理…...
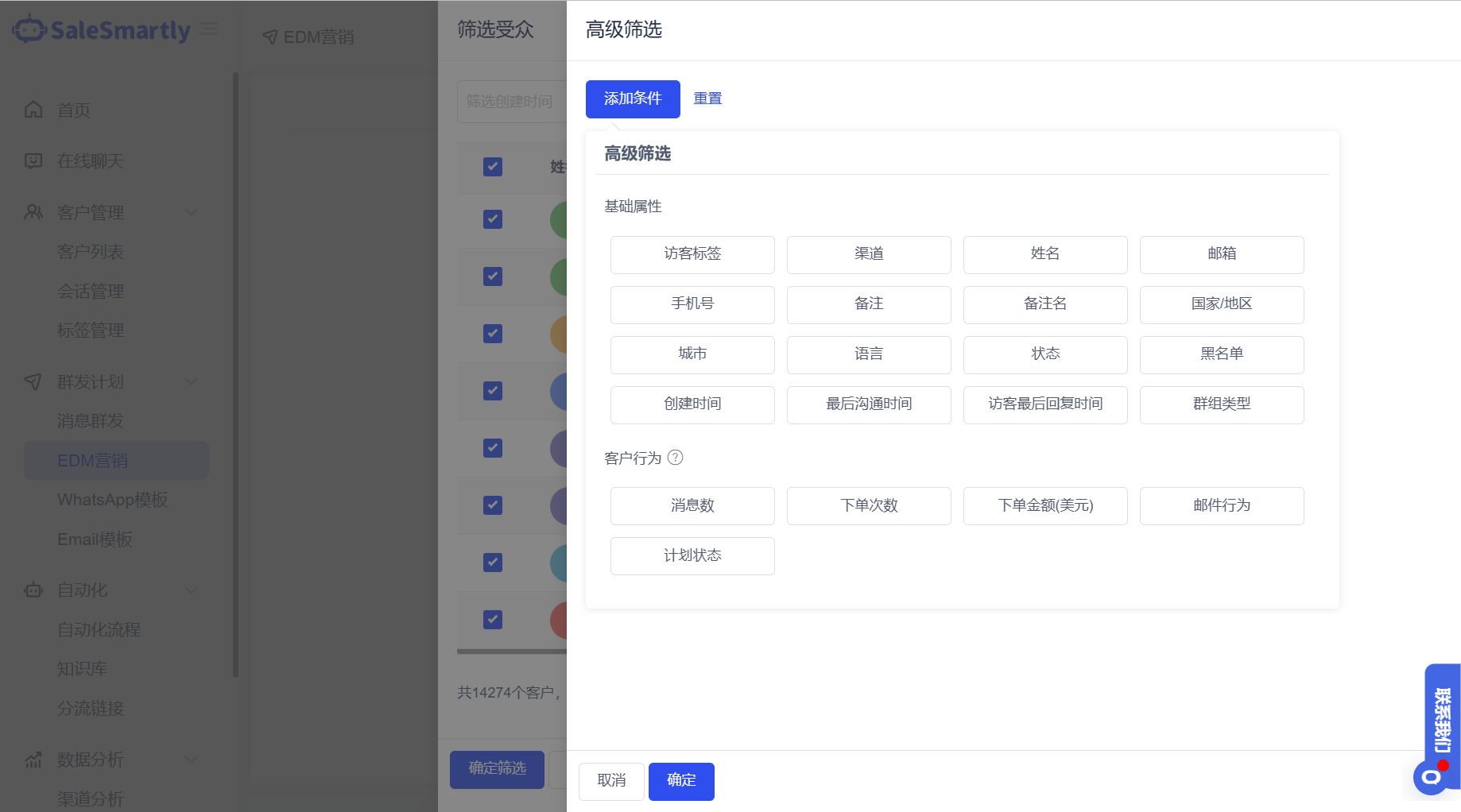
EDM营销过时了?不,这才是跨境电商成功的最佳工具
根据最近的一项研究,电子邮件仍然是最具说服力的营销工具和沟通形式之一。虽然即时通讯等其他渠道正在扎根,但电子邮件仍然是影响最深远的商业交流形式。到2023年,每天发送和接收的电子邮件总数可能会超过333亿封。所以,如果您希望…...

【大数据之Hive】二十五、HQL语法优化之小文件合并
1 优化说明 小文件优化可以从两个方面解决,在Map端输入的小文件合并,在Reduce端输出的小文件合并。 1.1 Map端输入文件合并 合并Map端输入的小文件是指将多个小文件分到同一个切片中,由一个Map Task处理,防止单个小文件启动一个M…...

spring 连接oracle数据库报错{dataSource-1} init error解决,电脑用户名问题
错误描述: 连接oracle数据就报错,同样的代码其他电脑不会报错。 报错如下: {dataSource-1} init error java.sql.SQLRecoverableException: IO 错误: Undefined Error com.alibaba.druid.pool.DruidDataSource-1049[main]ERROR: {dataSourc…...

行业视野::人工智能与机器人
控制和机器人领域非常重要的quote:莫拉维克悖论(Moravecs paradox) It is comparatively easy to make computers exhibit adult level performance on intelligence tests or playing checkers,and difficult or impossible to give them th…...

【Python入门系列】第十七篇:Python大数据处理和分析
【Python入门系列】第十七篇:Python大数据处理和分析 文章目录 前言一、数据处理和分析步骤二、Python大数据处理和分析库三、Python大数据处理和分析应用1、数据清洗和转换2、数据分析和统计3、数据可视化4、机器学习模型训练和预测5、大规模数据处理和分布式计算6…...
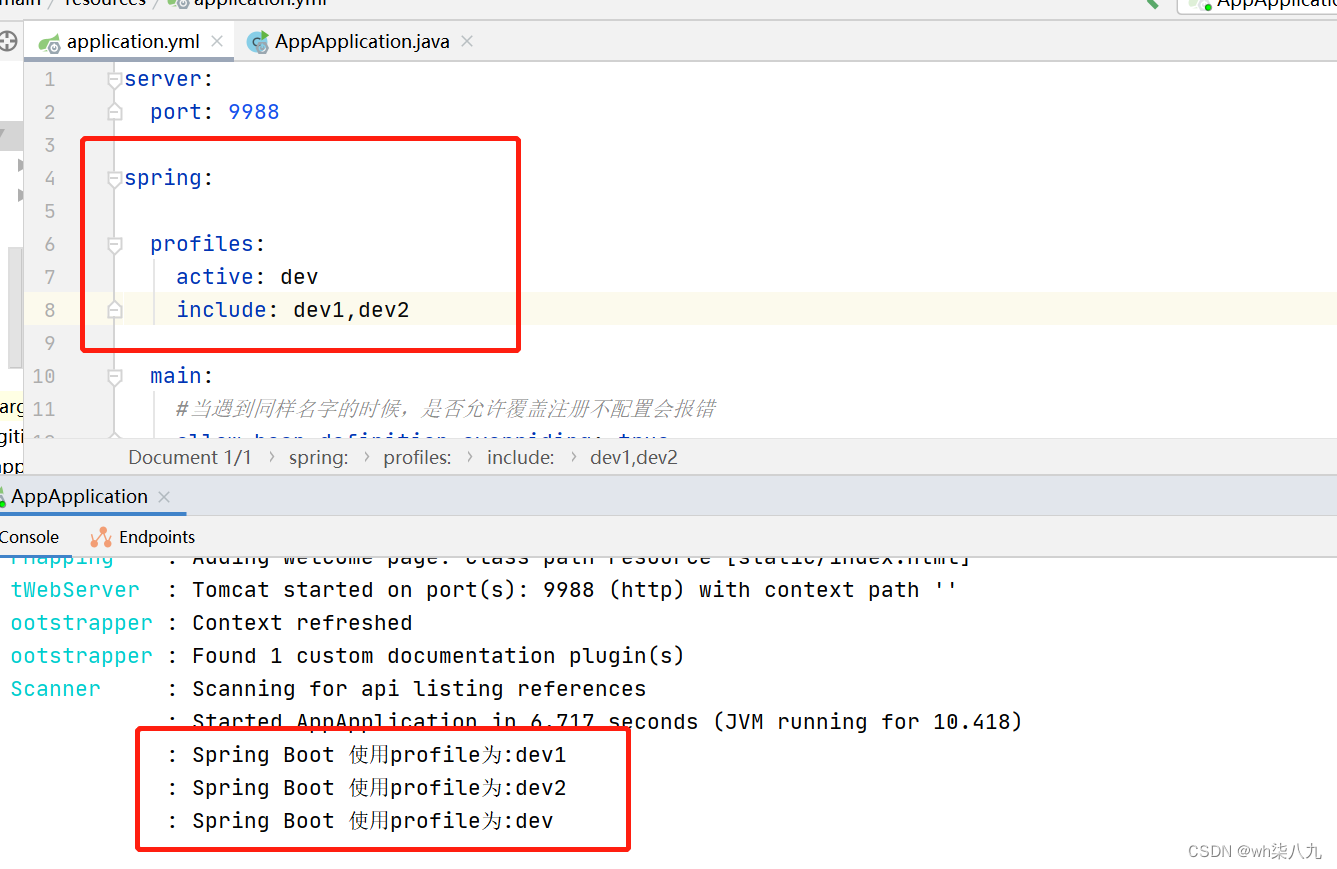
spring.profiles的使用详解
本文来说下spring.profiles.active和spring.profiles.include的使用与区别 文章目录 业务场景spring.profiles.active属性启动时指定 spring.profiles.include属性配置方法配置位置配置区别 用示例来使用和区分测试一测试二测试三 编写程序查看激活的yml文件本文小结 业务场景 …...
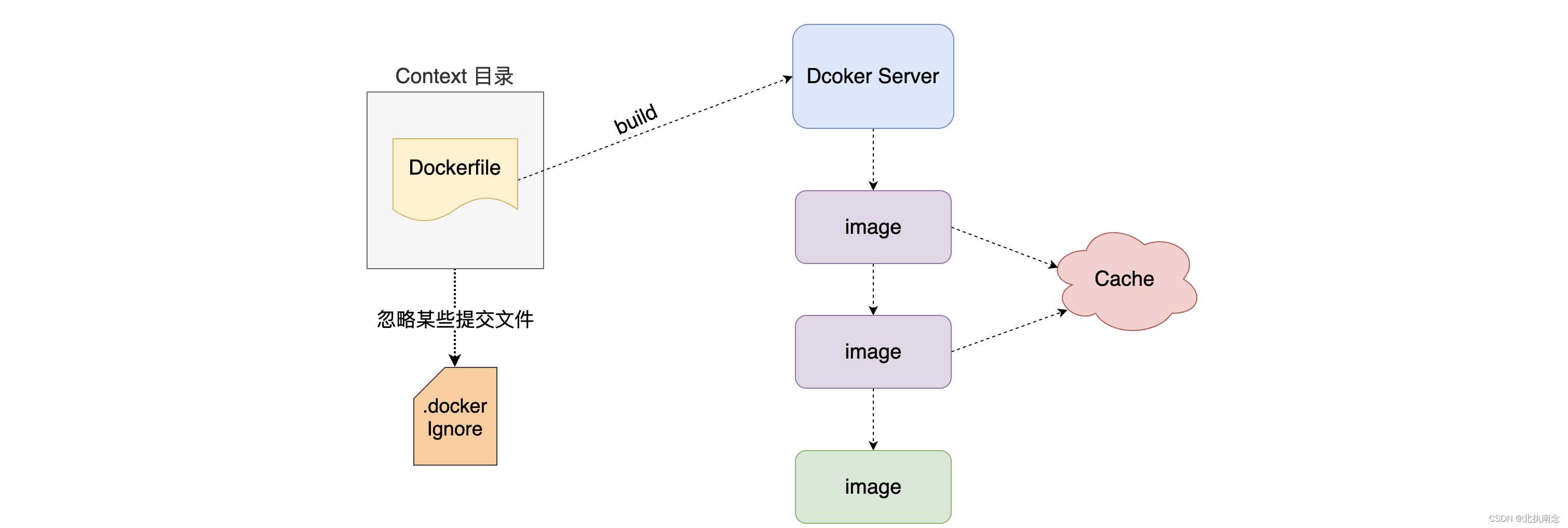
Docker使用总结
Docker 1.什么是 Docker 官网的介绍是“Docker is the world’s leading software container platform.” 官方给Docker的定位是一个应用容器平台。 Docker 是一个容器平台的领导者 Docker 容器平台 Docker 应用容器平台 application项目 Mysql Redis MongoDB ElasticSeacrh …...

MySQL 数据库的备份与还原案例分享 2023.07.12
/** 素材一 备份与还原 **/ 1 创建数据库booksDB mysql> create database booksDB; Query OK, 1 row affected (0.00 sec)2.1 创建booksDB表 mysql> use booksDB Database changed mysql> CREATE TABLE books-> (-> bk_id INT NOT NULL PRIMARY KEY,-> …...
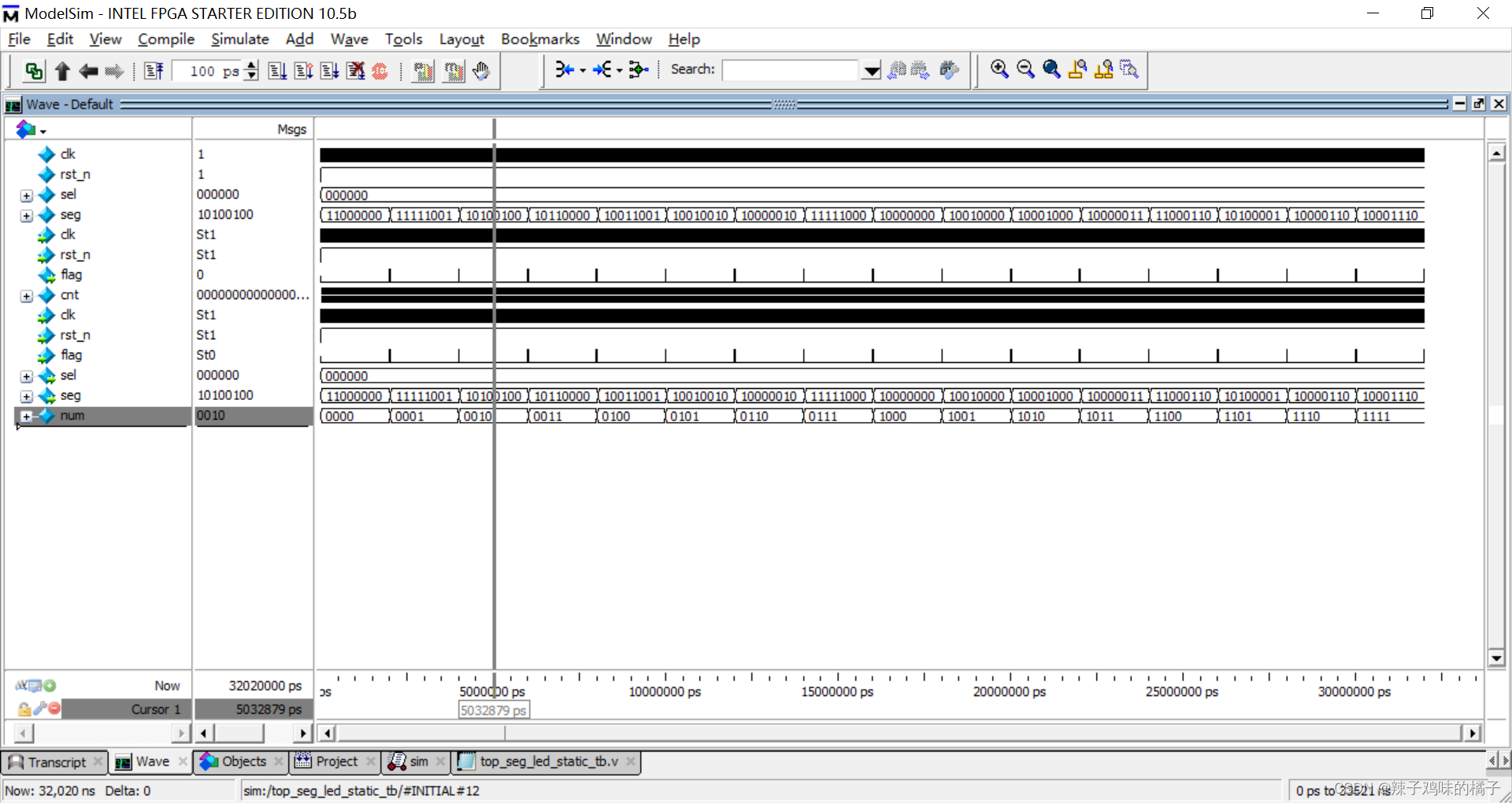
verilog实现数码管静态显示
文章目录 verilog实现数码管静态显示一、任务要求二、实验代码三、仿真代码四、仿真结果五、总结 verilog实现数码管静态显示 一、任务要求 六个数码管同时间隔0.5s显示0-f。要求:使用一个顶层模块,调用计时器模块和数码管静态显示模块。 二、实验代码…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
