【算法与数据结构】222、LeetCode完全二叉树的节点个数
文章目录
- 一、题目
- 二、一般遍历解法
- 三、利用完全二叉树性质
- 四、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目
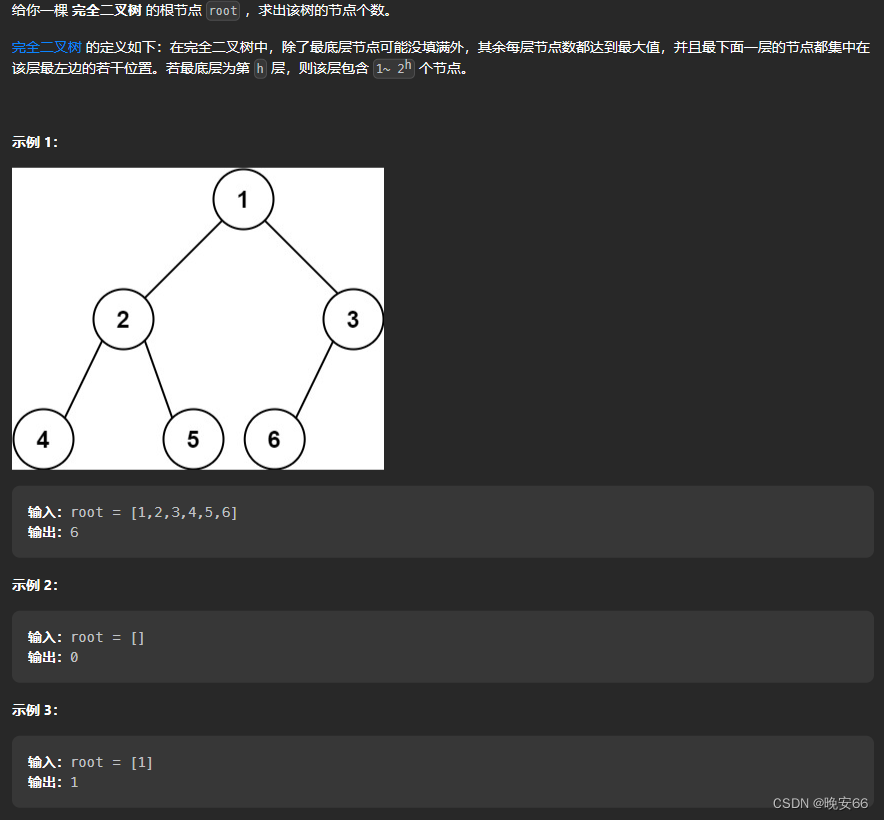
二、一般遍历解法
思路分析:利用层序遍历,然后用num++记录节点数量。其他的例如递归法和迭代法也是如此。
层序遍历程序如下:
class Solution {
public:int countNodes(TreeNode* root) {if (!root) return 0;queue<TreeNode*> que;que.push(root);int num = 0; // 节点数量while (!que.empty()) {int size = que.size(); // size必须固定, que.size()是不断变化的for (int i = 0; i < size; ++i) { TreeNode* node = que.front();que.pop();num++;if (node->left) que.push(node->left); // 空节点不入队if (node->right) que.push(node->right);}}return num;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( n ) O(n) O(n)。
递归程序如下(这应该是最精简的版本了):
class Solution2 {
public:int countNodes(TreeNode* root) {return root == NULL ? 0 : countNodes(root->left) + countNodes(root->right) + 1;}
};
三、利用完全二叉树性质
思路分析:完全二叉树具有一个特性,假设它的深度为K,它的节点个数在 [ 2 K − 1 − 1 , 2 K − 1 ] [2^{K-1}-1, 2^K-1] [2K−1−1,2K−1]之间,意味着它只有两种情况,一种是满二叉树,一种是最后一层叶子节点没有满。对于情况一可以用 2 K − 1 2^K-1 2K−1来计算,对于情况二分别递归其左子树和右子树,递归到一定深度一定有左子树或者右子树为满二叉树,然后按照情况一来计算。那么满二叉树的最左边节点和最右边节点的深度一定是相等的,依据这个特性判断子树是否为满二叉树。

递归程序当中,我们要确定三个步骤,1、输入参数,返回值 2、递归终止条件 3、单层递归逻辑。输入参数为中间节点,返回值为左子树的节点数量+右子树节点数量+1(+1是加上中间节点)。当节点为空时,递归终止,返回0。每次递归我们都要计算最左/右边节点深度,然后判断二者是否相等,如果相等则是满二叉树,返回 2 K − 1 2^K-1 2K−1,K为深度。程序当中使用了左移运算符,因为运算符的优先级问题,记得加括号。左移运算符是二进制运算,计算机计算的更快。
程序如下:
class Solution3 {
public:// 利用完全二叉树的性质,递归法int countNodes(TreeNode* root) {if (!root) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int Ldepth = 0, Rdepth = 0;while (left) { // 递归左子树left = left->left;Ldepth++;}while (right) { // 递归右子树right = right->right;Rdepth++;}if (Ldepth == Rdepth) {return (2 << Ldepth) - 1; // <<为左移运算符(位运算符),相当于2*leftDepth,但二进制运算计算机算的更快}return countNodes(root->left) + countNodes(root->right) + 1;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( n ) O(n) O(n)。
四、完整代码
# include <iostream>
# include <vector>
# include <queue>
# include <string>
# include <algorithm>
using namespace std;// 树节点定义
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};class Solution {
public:// 层序遍历法int countNodes(TreeNode* root) {if (!root) return 0;queue<TreeNode*> que;que.push(root);int num = 0; // 节点数量while (!que.empty()) {int size = que.size(); // size必须固定, que.size()是不断变化的for (int i = 0; i < size; ++i) { TreeNode* node = que.front();que.pop();num++;if (node->left) que.push(node->left); // 空节点不入队if (node->right) que.push(node->right);}}return num;}
};class Solution2 {
public:int countNodes(TreeNode* root) {return root == NULL ? 0 : countNodes(root->left) + countNodes(root->right) + 1;}
};class Solution3 {
public:// 利用完全二叉树的性质,递归法int countNodes(TreeNode* root) {if (!root) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int Ldepth = 0, Rdepth = 0;while (left) { // 递归左子树left = left->left;Ldepth++;}while (right) { // 递归右子树right = right->right;Rdepth++;}if (Ldepth == Rdepth) {return (2 << Ldepth) - 1; // <<为左移运算符(位运算符),相当于2*leftDepth,但二进制运算计算机算的更快}return countNodes(root->left) + countNodes(root->right) + 1;}
};void my_print(vector <string>& v, string msg)
{cout << msg << endl;for (vector<string>::iterator it = v.begin(); it != v.end(); it++) {cout << *it << " ";}cout << endl;
}void my_print2(vector<vector<int>>& v, string str) {cout << str << endl;for (vector<vector<int>>::iterator vit = v.begin(); vit < v.end(); ++vit) {for (vector<int>::iterator it = (*vit).begin(); it < (*vit).end(); ++it) {cout << *it << ' ';}cout << endl;}
}// 前序遍历迭代法创建二叉树,每次迭代将容器首元素弹出(弹出代码还可以再优化)
void Tree_Generator(vector<string>& t, TreeNode*& node) {if (t[0] == "NULL" || !t.size()) return; // 退出条件else {node = new TreeNode(stoi(t[0].c_str())); // 中t.assign(t.begin() + 1, t.end());Tree_Generator(t, node->left); // 左t.assign(t.begin() + 1, t.end());Tree_Generator(t, node->right); // 右}
}// 层序遍历
vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> que;if (root != NULL) que.push(root);vector<vector<int>> result;while (!que.empty()) {int size = que.size(); // size必须固定, que.size()是不断变化的vector<int> vec;for (int i = 0; i < size; ++i) {TreeNode* node = que.front();que.pop();vec.push_back(node->val);if (node->left) que.push(node->left); // 空节点不入队if (node->right) que.push(node->right);}result.push_back(vec);}return result;
}int main()
{vector<string> t = { "1", "2", "4", "NULL", "NULL", "5", "NULL", "NULL", "3", "6", "NULL", "NULL", "NULL"}; // 前序遍历my_print(t, "目标树");TreeNode* root = new TreeNode();Tree_Generator(t, root);vector<vector<int>> tree = levelOrder(root);my_print2(tree, "目标树:");Solution2 s1;int result = s1.countNodes(root);cout << "节点数量为:" << result << endl;system("pause");return 0;
}
end
相关文章:

【算法与数据结构】222、LeetCode完全二叉树的节点个数
文章目录 一、题目二、一般遍历解法三、利用完全二叉树性质四、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、一般遍历解法 思路分析:利用层序遍历,然后用num记录节点数量。其他的例如…...

登录和注册表单的11个HTML最佳实践
原文:11 HTML best practices for login & sign-up forms 原作者:Andrey Sitnik 翻译已获原文作者许可,禁止转载和商用 大多数网站都有登录或注册表单;它们是业务转换的关键部分。然而,即使是流行的站点也没有实现本文中提到的…...

Mysql删除历史数据
Mysql定时删除历史数据 实现 1.创建存储过程(函数) SQL DROP PROCEDURE IF EXISTS KeepDatasWith30Days CREATE PROCEDURE KeepDatasWith30Days() BEGINSELECT maxId:max(Id) FROM tableName WHERE CreateTime<DATE(DATE_SUB(NOW(),INTERVAL 31 D…...

Python—数据结构(一)
先放一张自己学习和整理归纳的思维导图,以便让大家都知道我自己的整体学习路线。 数据结构的学习路上内容枯燥,但坚持下来一定有很大的收获!加油💪🏻! 数据结构 数据的概念数据元素: 若干基本…...

离线环境安装flask依赖包
找到当前版本需要的所有依赖包,生产flask项目生成项目依赖包文件requirements.txt 1)在当前项目目录下 生成requirements文件:pip freeze >requirements.txt 执行requirements文件,安装依赖包:pip install -r requirements.t…...
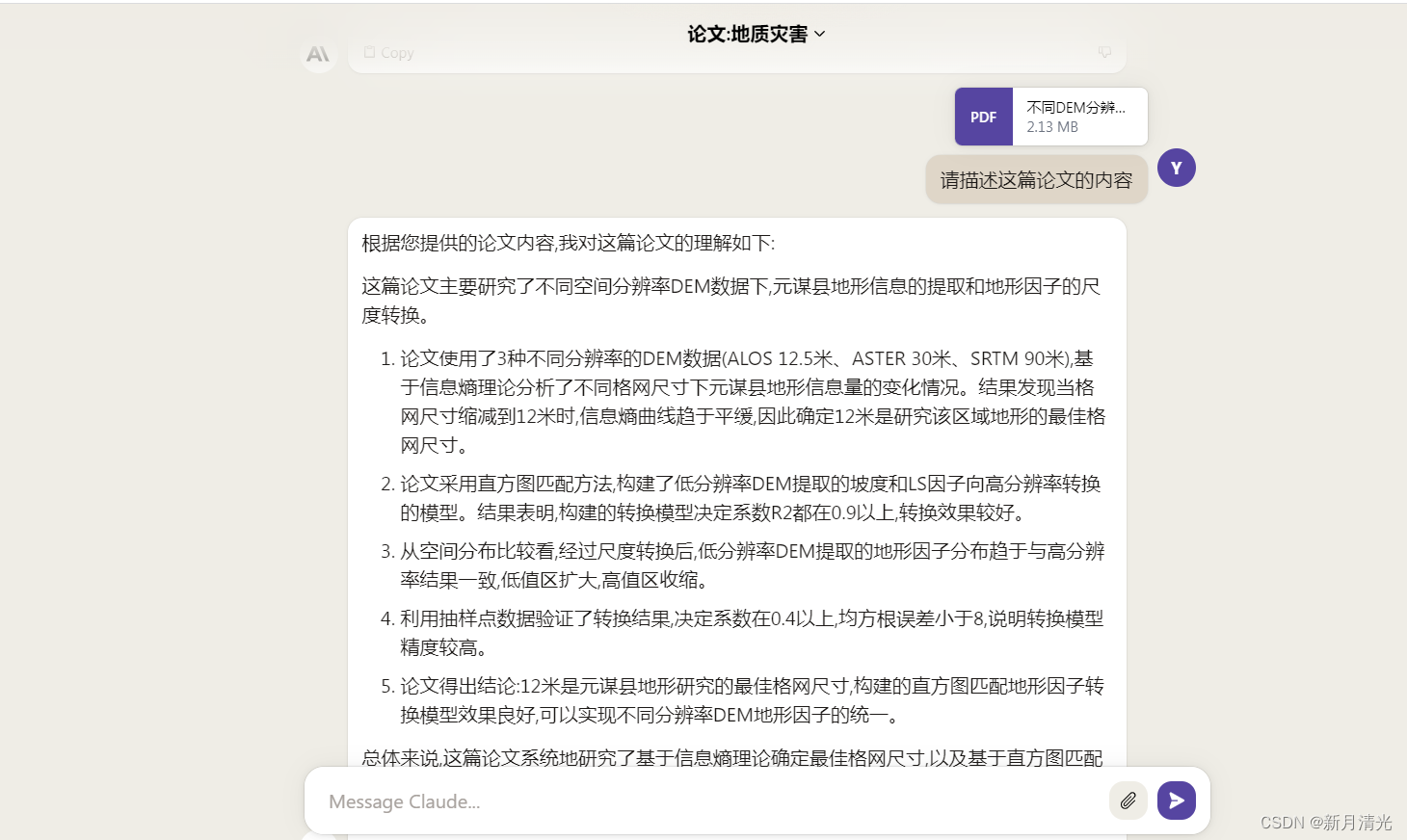
ChatGPT与Claude对比分析
一 简介 1、ChatGPT: 访问地址:https://chat.openai.com/ 由OpenAI研发,2022年11月发布。基于 transformer 结构的大规模语言模型,包含1750亿参数。训练数据集主要是网页文本,聚焦于流畅的对话交互。对话风格友好,回复通顺灵活,富有创造性。存在一定的安全性问题,可…...

登录和注册页面 - 验证码功能的实现
目录 1. 生成验证码 2. 将本地验证码发布成 URL 3. 后端返回验证码的 URL 给前端 4. 前端将用户输入的验证码传给后端 5. 后端验证验证码 1. 生成验证码 使用hutool 工具生成验证码. 1.1 添加 hutool 验证码依赖 <!-- 验证码 --> <dependency><groupId…...

HDFS的文件块大小(重点)
HDFS 中的文件在物理上是分块存储 (Block ) , 块的大小可以通过配置参数( dfs.blocksize)来规定,默认大小在Hadoop2.x/3.x版本中是128M,1.x版本中是64M。 如果一个文件文件小于128M,该文件会占…...
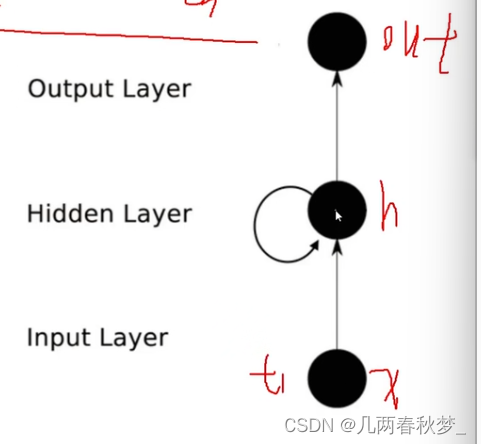
深度学习(二)
目录 一、神经网络 整体架构: 架构细节: 神经元个数的影响: 神经网络过拟合解决: 卷积网络 整体架构: 卷积层 边缘填充 特征尺寸计算 池化层 特征图变化 递归神经网络 一、神经网络 整体架构: 图中分别为输入层、隐层1、隐层2、输出层 通过输入层输入某数值…...
方法函数)
无涯教程-jQuery - wrapInner( html )方法函数
wrapInner(html)方法使用HTML结构包装每个匹配元素(包括文本节点)的内部子内容。 wrapInner( html ) - 语法 selector.wrapInner( html ) 这是此方法使用的所有参数的描述- html - 将动态创建并环绕目标的HTML字符串。 wrapInner( html ) - 示例 以下是一个简单的示例…...
【unity之IMGUI实践】单例模式管理数据存储【二】
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...

【C++】开源:Linux端ALSA音频处理库
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍Linux端ALSA音频处理库。 无专精则不能成,无涉猎则不能通。。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜欢的朋友可以关注一下,…...

【Linux | Shell】结构化命令2 - test命令、方括号测试条件、case命令
目录 一、概述二、test 命令2.1 test 命令2.2 方括号测试条件2.3 test 命令和测试条件可以判断的 3 类条件2.3.1 数值比较2.3.2 字符串比较 三、复合条件测试四、if-then 的高级特性五、case 命令 一、概述 上篇文章介绍了 if 语句相关知识。但 if 语句只能执行命令,…...

基于单片机的语音识别智能垃圾桶垃圾分类的设计与实现
功能介绍 以51单片机作为主控系统;液晶显示当前信息和状态;通过语音识别模块对当前垃圾种类进行语音识别; 通过蜂鸣器进行声光报警提醒垃圾桶已满;采用舵机控制垃圾桶打开关闭;超声波检测当前垃圾桶满溢程度࿱…...
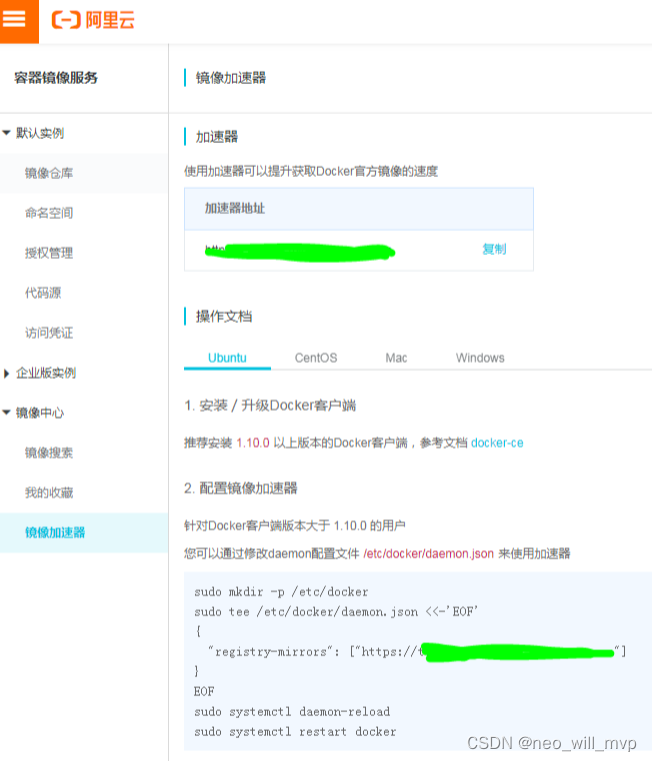
最新版本docker 设置国内镜像源 加速办法
解决问题:加速 docker 设置国内镜像源 目录: 国内加速地址 修改方法 国内加速地址 1.Docker中国区官方镜像 https://registry.docker-cn.com 2.网易 http://hub-mirror.c.163.com 3.ustc https://docker.mirrors.ustc.edu.cn 4.中国科技大学 https://docker.mirrors…...
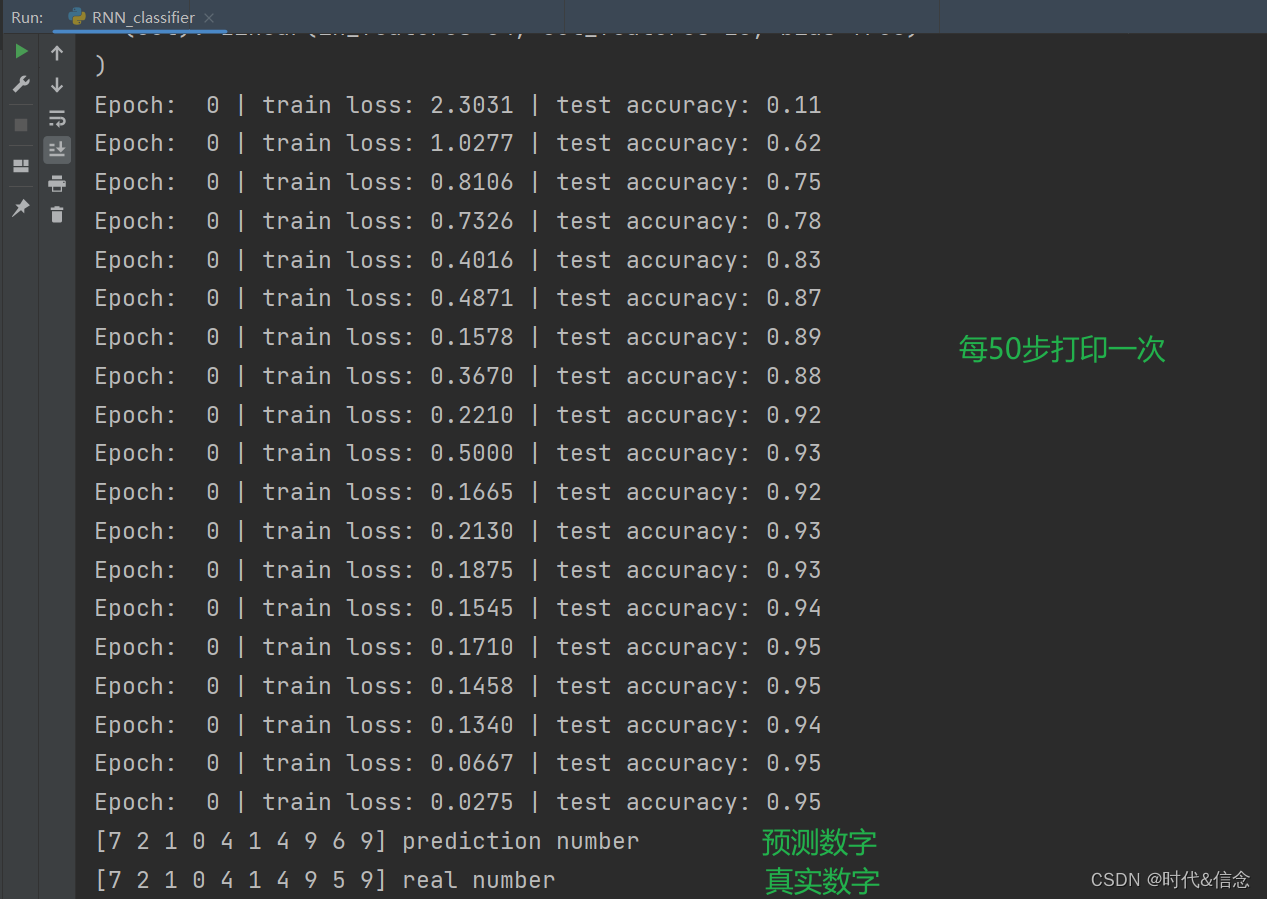
深度学习——LSTM解决分类问题
RNN基本介绍 概述 循环神经网络(Recurrent Neural Network,RNN)是一种深度学习模型,主要用于处理序列数据,如文本、语音、时间序列等具有时序关系的数据。 核心思想 RNN的关键思想是引入了循环结构,允许…...
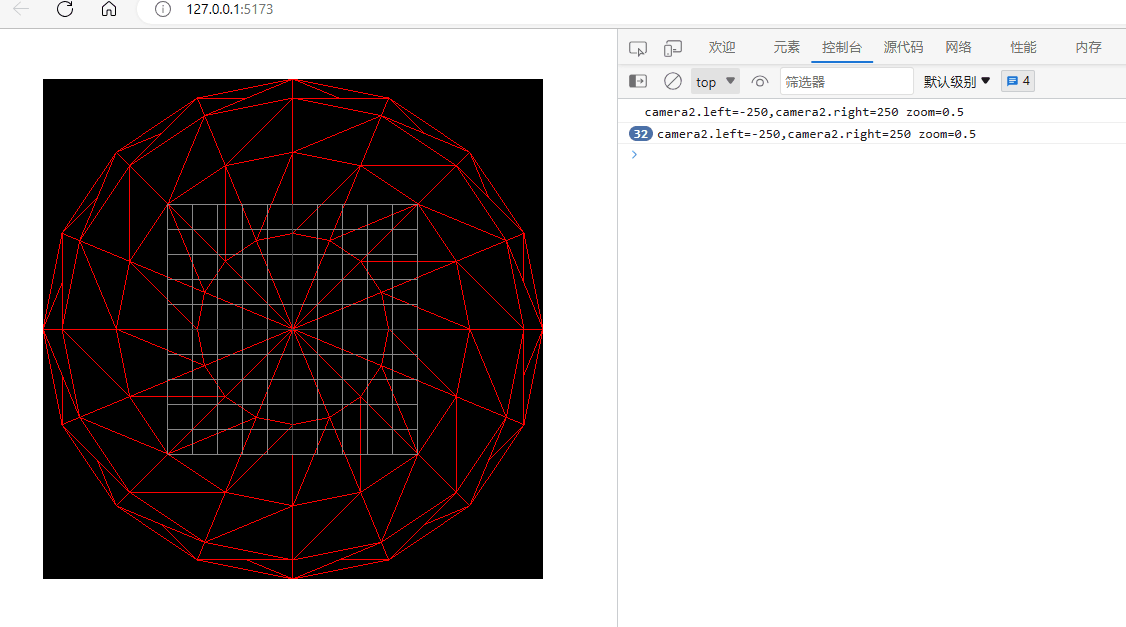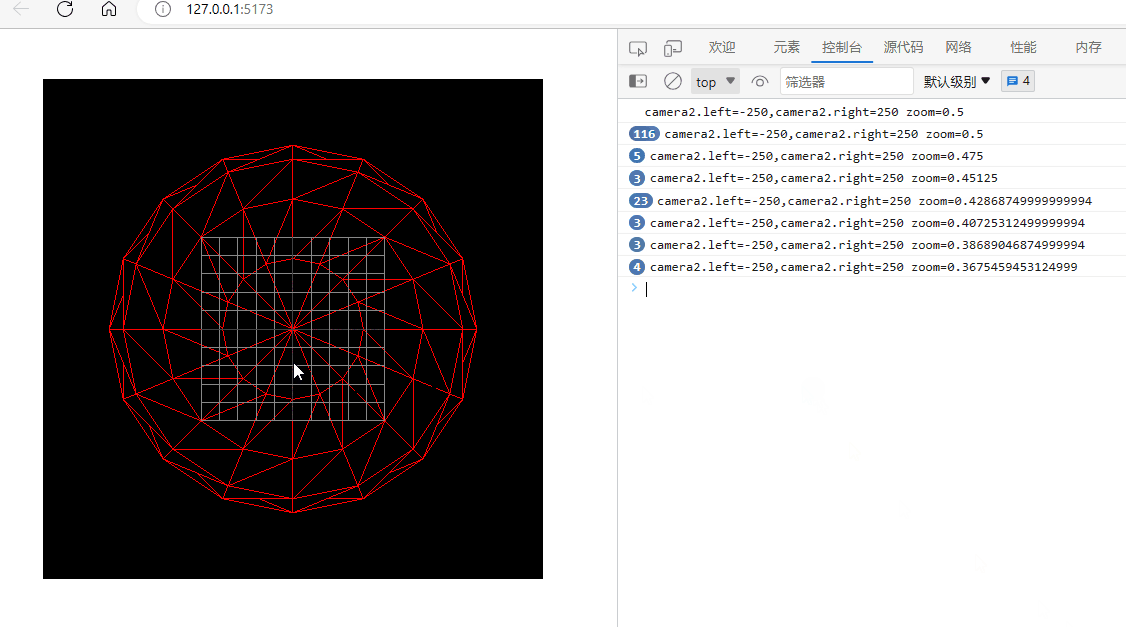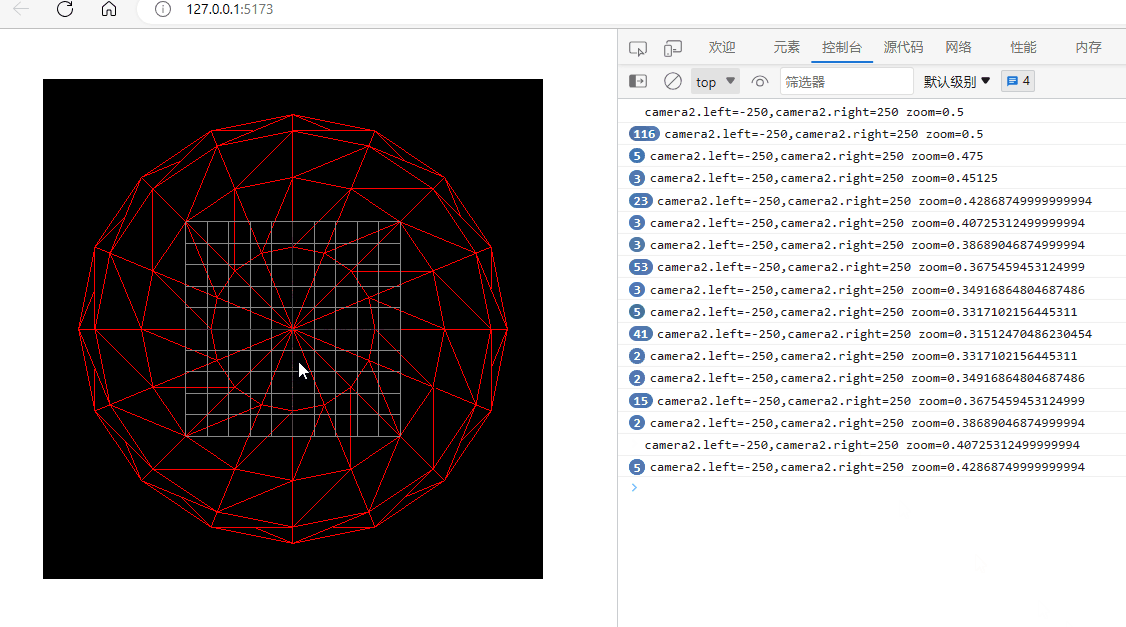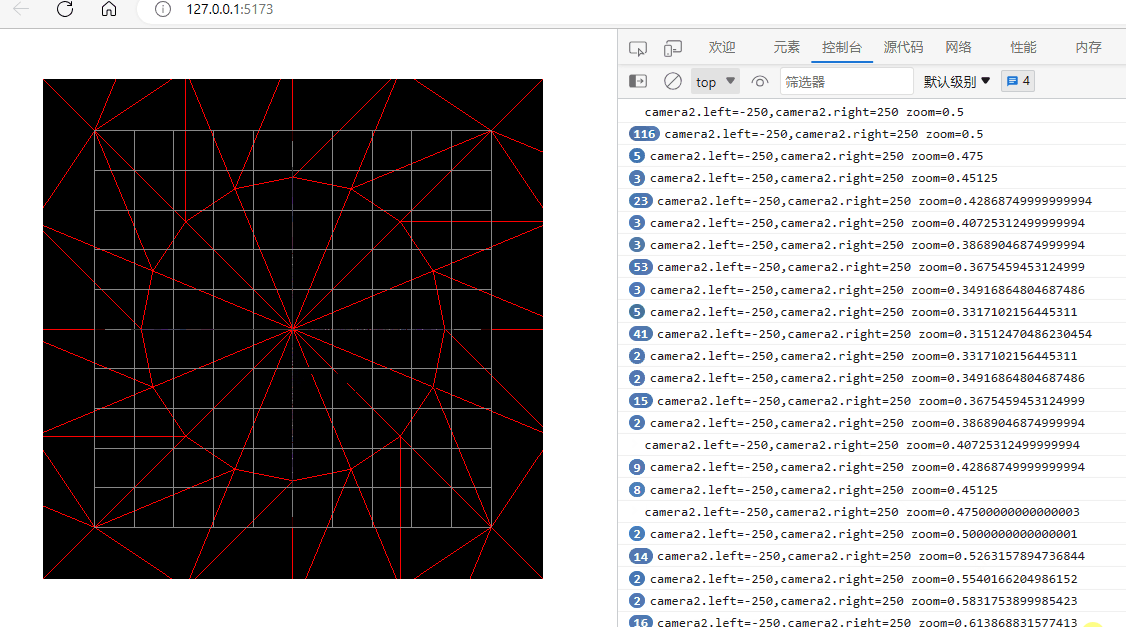
three.js入门二:相机的zoom参数
环境: threejs:129 (在浏览器的控制台下输入: window.__THREE__即可查看版本)vscodewindowedge 透视相机或正交相机都有一个zoom参数,它可以用来将相机排到的内容在canvas上缩放显示。 注意:…...
实例)
sql语法树(select)实例
在SELECT节点下,将"*"(表示选择所有列)添加为子节点。下面是一个简单的SQL语句示例: SELECT * FROM customers WHERE age > 25 AND city New York;语法树(Syntax Tree)是由SQL解析器构建的…...
爬虫002_python程序的终端运行_文件运行_ipython的使用---python工作笔记020
用python运行一个文件,就是要写一个.py结尾的文件 然后保存 然后直接cmd中,python 然后写上py文件的路径就可以了 然后看一下内容 看一下终端中运行,直接输入python进入python环境,然后写python代码 回车运行 退出可以用exit()...
智融SW3518S降压协议IC一款适合车充控制芯片
描述 SW3518S 是一款高集成度的多快充协议双口充电芯片, 支持 AC 口任意口快充输出, 支持双口独立限流。 其集成了 5A 高效率同步降压变换器, 支持 PPS/PD/QC/AFC/FCP/SCP/PE/SFCP/VOOC等多种快充协议, 最大输出 PD 100Wÿ…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
