学生管理系统-05封装选项卡
一、选项卡的添加
1、在router/index.js修改之前的动态添加二级路由的代码
router.addRoute("homeName",{ path:routeObj.path, component:()=>import(`@/views${routeObj.permission}.vue`), meta:{ name:routeObj.title }})在vue-router这个路由插件中,route表示的是路由对象,route的常见属性
| 属性名 | 含义 |
|---|---|
| path | 路径 |
| component | 路由对应的组件对象 |
| name | 路由名称 |
| children | 子路由配置 |
| meta | 路由元信息(携带额外信息) |
这里我们使用路由元信息,将选项卡的名称携带到路由对象上
2、在components文件下创建MyTags.vue组件,该组件用于完成封装的功能
<template> <div> <el-tag v-for="(item,index) in historyAry" :key="index"> <router-link :to="item.path&相关文章:

学生管理系统-05封装选项卡
一、选项卡的添加 1、在router/index.js修改之前的动态添加二级路由的代码 router.addRoute("homeName",{ path:routeObj.path, component:()=>import(`@/views${routeObj.permission}.vue`), meta:{ name:routeObj.title …...

关于一些C++、Qt、Python方面的术语
杂鱼之前纯粹用python没细致理解过的术语整理一下,常看常新( 定义 (Definition): 定义是指给一个实体分配内存空间,以便在程序中使用。在C和Python中,这个实体可以是变量、函数或类。在C中,定义通常是在声…...

k8s中强制删除pv
K8s 集群内有一个已经不再使用的 PV,虽然已经删除了与其关联的 Pod 及 PVC,并对其执行了删除命令,但仍无法正常删除,一直处于 Terminating 状态: 解决办法: 1. 获取pv信息 kubectl get pv 2. 解除pv锁定 …...

60寸透明屏的透明度怎么样?
60寸透明屏是一种新型的显示屏技术,它具有透明度高、色彩鲜艳、清晰度高等特点,可以广泛应用于商业展示、户外广告、智能家居等领域。 首先,60寸透明屏的透明度高。 透明屏采用了特殊的材料和技术,使得屏幕在显示内容的同时&…...
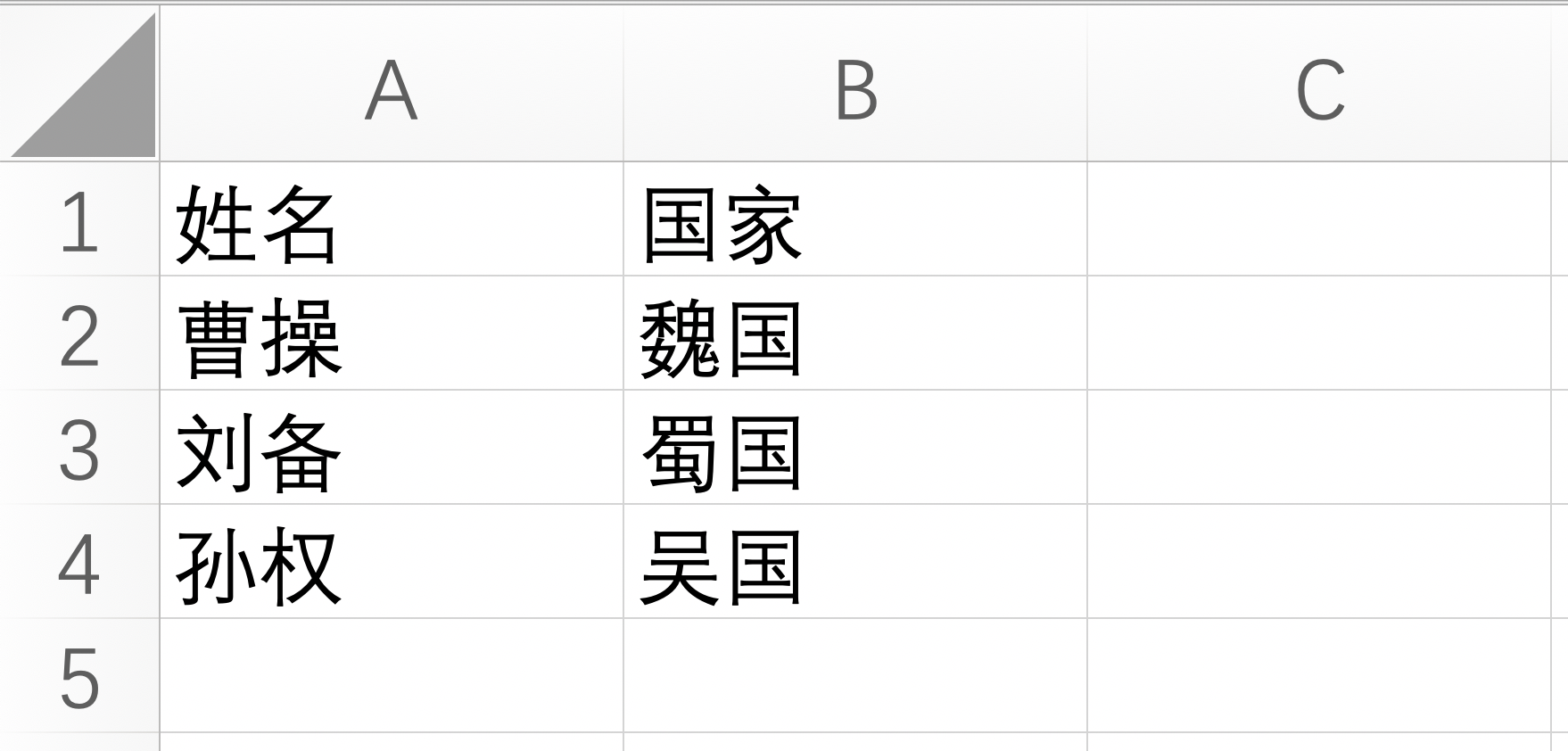
Python:使用openpyxl读取Excel文件转为json数据
文档 https://openpyxl.readthedocs.io/en/stable/https://pypi.org/project/openpyxl/ 安装 pip install openpyxl环境 $ python --version Python 3.7.0读取文件示例:将Excel文件读取为json数据 有如下一个文件 data.xlsx 实现代码 # -*- coding: utf-8 -…...
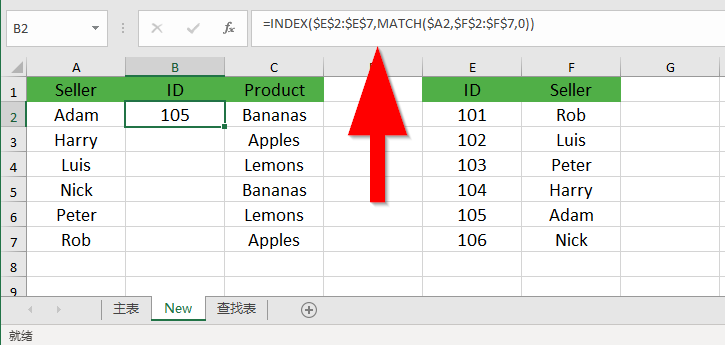
在Microsoft Excel中如何快速合并表格
在 Excel 中分析数据时,在一个工作表中收集所有必要信息的频率是多少?几乎从来没有!当不同的数据分散在许多工作表和工作簿中时,这是一种非常常见的情况。幸运的是,有几种不同的方法可以将多个表中的数据组合成一个表&…...

【RS】基于规则的面向对象分类
ENVI使用最多的工具就是分类,这也是很多卫星影像的用途。在ENVI中有很多分类工具,如最基础的监督分类(最大似然法、最小距离、支持向量机、随机森林)、非监督分类(K-means、IsoData),还有面向对…...
SWF格式视频怎么转换成AVI格式?简单的转换方法分享
当你想要在不同的设备上播放视频时,将SWF格式视频转换成AVI格式是非常有用的。因为SWF格式通常只能在特定的软件或网页上播放,而AVI格式则可以在更广泛的设备上播放,包括智能手机,平板电脑和电视机等。那么我们怎么将SWF转换成AVI…...
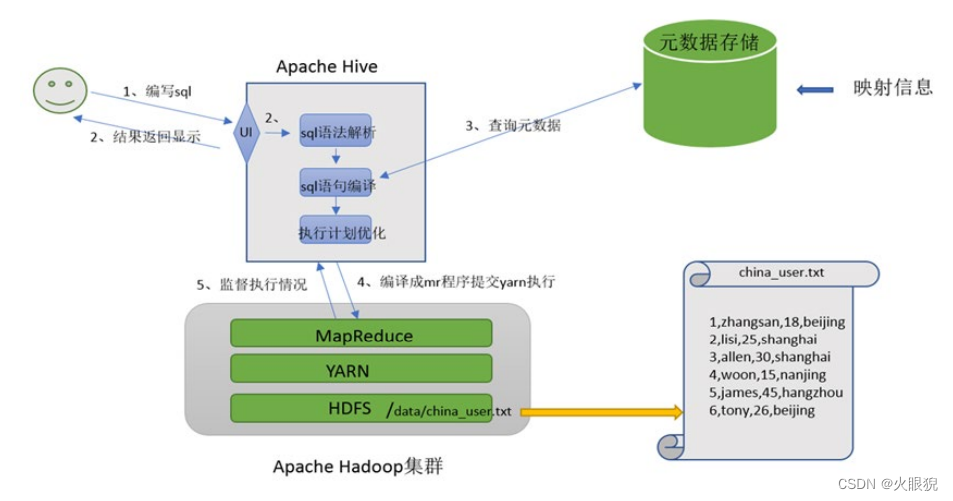
Hive数据仓库
数据仓库概念与起源发展由来 数仓概念 数据仓库(英语:Data Warehouse,简称数仓、DW),是一个用于存储、分析、报告的数据系统。数据仓库的目的是构建面相分析的集成化数据环境,分析结果为企业提供决策支持…...
公网访问的Linux CentOS本地Web站点搭建指南
文章目录 前言1. 本地搭建web站点2. 测试局域网访问3. 公开本地web网站3.1 安装cpolar内网穿透3.2 创建http隧道,指向本地80端口3.3 配置后台服务 4. 配置固定二级子域名5. 测试使用固定二级子域名访问本地web站点 前言 在web项目中,部署的web站点需要被外部访问,则…...

ChatGPT:人机交互新境界,AI智能引领未来
一、ChatGPT:智能交流的新标杆 ChatGPT是基于GPT技术的最新版本,拥有深度学习模型的基因。它通过在大量数据上进行预训练,可以理解和生成自然语言,从而实现了与人类更加自然流畅的对话和交流。 二、ChatGPT的技术背景和工作原理 …...

微信小程序值相同的数据,一个数据setDate修改后,另一个值相同的数据也会修改
在js中一个基础类型可以直接赋值,引用类型直接赋值会指向同一个值(原理是浅拷贝和深拷贝) 解决问题代码:JSON.parse(JSON.stringify(json)) ↓ let json {0: [false, false],1: [true, false] } this.setData({timeList: JSON.…...
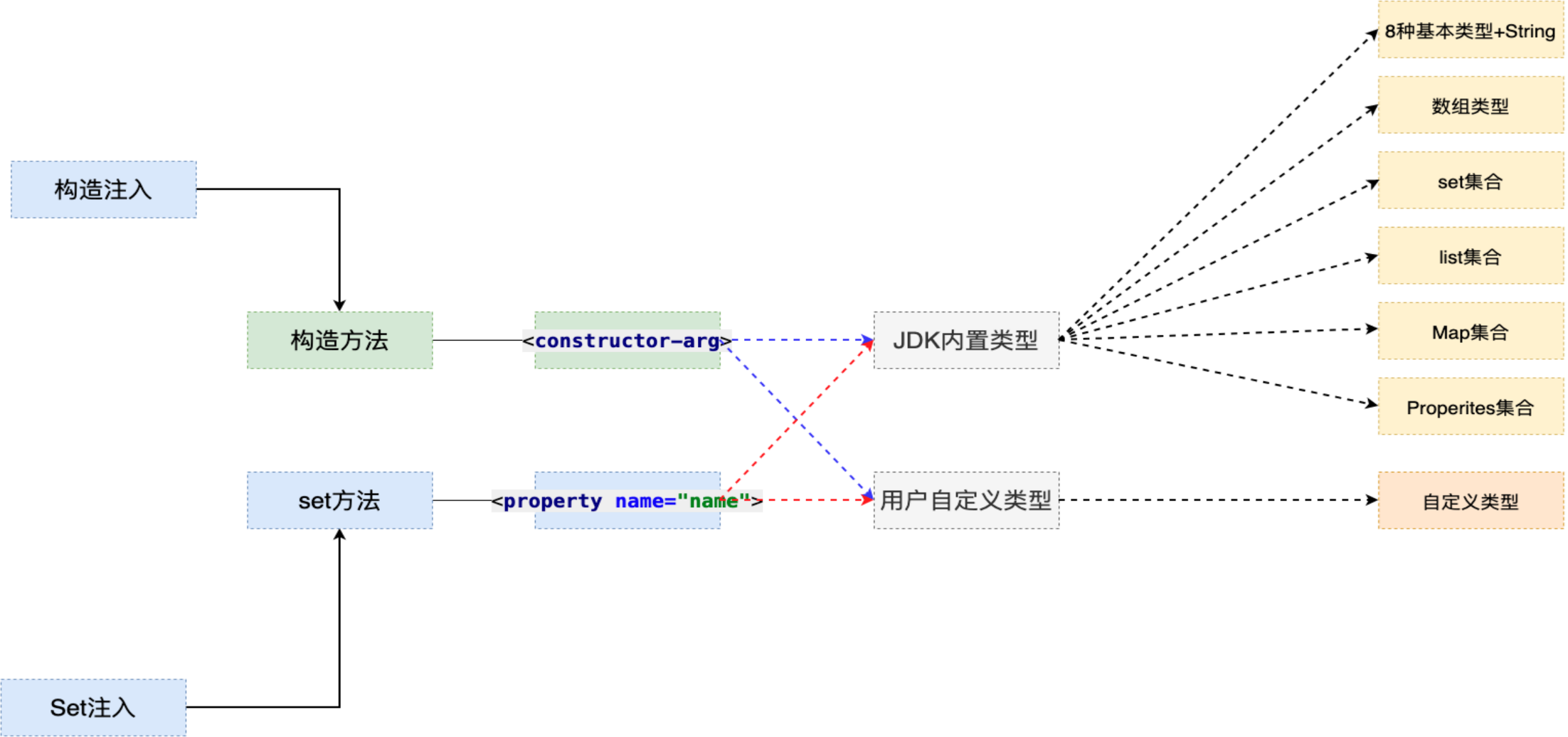
Spring5学习笔记 — IOC
✅作者简介:大家好,我是Cisyam,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Cisyam-Shark的博客 💞当前专栏: Spring专栏 ✨特色专栏&a…...
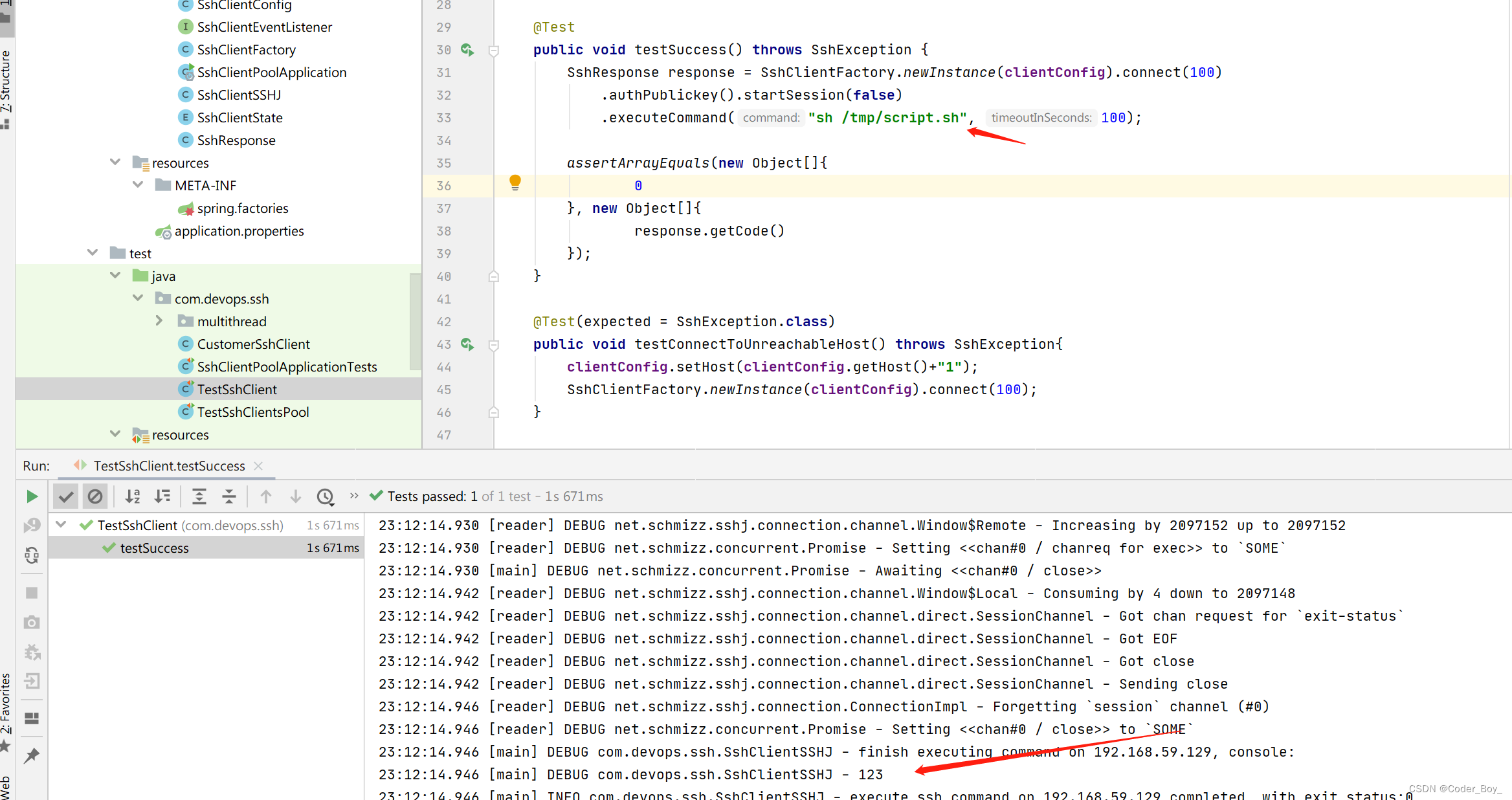
DevOps自动化平台开发之 Shell脚本执行的封装
基础知识 基于如下技术栈开发DevOps平台 Spring Boot Shell Ansible Git Gitlab Docker K8S Vue 1、spring boot starter的封装使用 2、Shell脚本的编写 3、Ansible 脚本的编写 4、Docker 的使用与封装设计 本篇介绍如何使用Java封装Linux命令和Shell脚本的使用 将其设计成…...
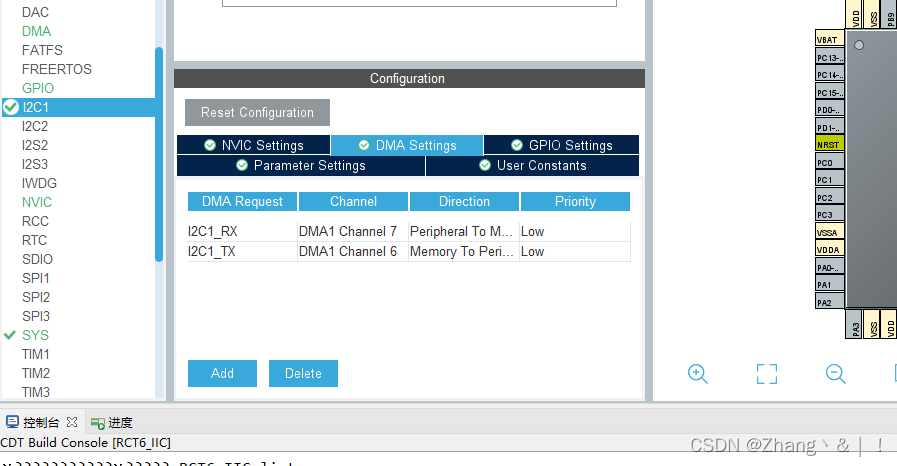
STM32CubeIDE(I2C)
目录 一、IIC轮询模式 1.1 配置 1.2 编写AHT20驱动 1.2.1 aht20.h 1.2.2 aht20.c 二、I2C中断 2.1 打开中断 2.2 分离读取流程 2.3 在主函数中重新编写读取流程 2.4 在i2c.c中重新定义stm32f1xx_hal_i2c.h中的两个函数 三、I2CDMA 3.1 配置DMA通道 3.2 代码的修改 一…...

http 请求报文响应报文的格式以及Token cookie session 区别
面试必备 http 请求报文响应报文的格式Token cookie session 区别 http 请求报文响应报文的格式 HTTP 请求报文和响应报文的格式如下: HTTP 请求报文格式: <方法> <路径> <协议版本> <请求头部字段1>: <值1> <请求头…...
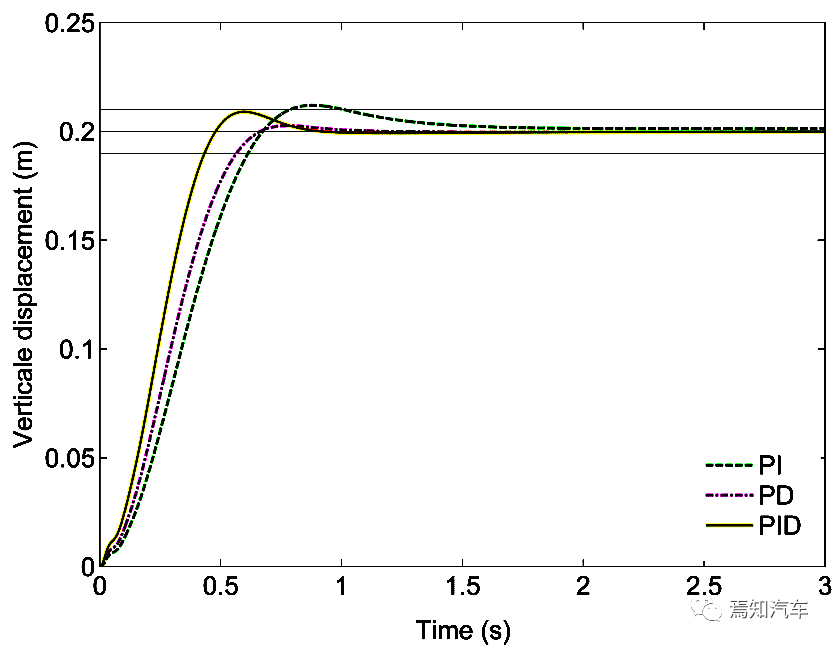
智能汽车的主动悬架工作原理详述
摘要: 本文将详细介绍主动悬架功能原理设计。 主动悬架是车辆上的一种汽车悬架。它使用车载系统来控制车轮相对于底盘或车身的垂直运动,而不是由大弹簧提供的被动悬架,后者的运动完全由路面决定。主动悬架分为两类:真正的主动悬架…...

vue2和vue3的一些技术点复习
二、vue2 1、vue2对已有组件二次封装,例如fes2 input 组件(文档链接) 子组件 <template><div class"keyboard-page"><wb-input:id"keyBoardId":placeholder"placeholder" :type"type&q…...

安装nvm 切换node版本
1. 安装 nvm curl -o- https://raw.githubusercontent.com/creationix/nvm/v0.33.1/install.sh | bash 验证nvm安装完成 command -v nvm 如果安装完成,就会显示如下 nvm 2. 查看 nvm 可以安装的 node 版本 查看可以安装的版本 nvm ls-remote 查看所有可以安装的…...

【html中的BFC是什么】
BFC(块级格式化上下文)是 CSS 中的一种盒模型布局,是指一个独立的块级容器,容器内部的元素会按照一定规则进行布局。 BFC 具体的规则有以下几个: BFC 内部的元素在垂直方向上相互排列,不会出现浮动的情况。…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
