25、matlab里面的10中优化方法介绍——Opt_Golden法(matlab程序)
1.简述
基本思想
黄金分割法也称为 0.618 法,其基本思想是通过取试探点和进行函数值比较,使包含极小点的搜索区间不断缩短以逼近极小值点。适用于确定区间上的任何单谷函数求极小值的问题。
公式推导
设有定义在[ a , b ] [a,b][a,b]上的单谷函数
φ ( α ) = f ( x k + α d k ) \varphi \left( \alpha \right) =f\left( x_k+\alpha d_k \right)
在[ a , b ] [a,b][a,b]上取两个试探点。计算φ ( x 1 )
可能会出现以下两种情形:
我们要求试探点满足下列两个原则:
对称原则
λ = 新 区 间 长 度 原 区 间 长 度 = \lambda =\frac{新区间长度}{原区间长度}=λ=
原区间长度
新区间长度
=定值(保持缩减比)
从而可得
{ x 1 = a + ( 1 − λ ) ( b − a ) x 2 = a + λ ( b − a )
考虑情形1,此时新的搜索区间为[ a 1 , b 1 ] [a_1,b_1][a
选取新的试探点x
若令λ 2 = 1 − λ ( λ > 0 ) \lambda ^2=1-\lambda\left( \lambda>0 \right)λ
则有
新的试探点x 4 x_4x
1−λ得λ ≈ 0.618 \lambda \approx0.618λ≈0.618。
具体练习及Matlab实现
2.代码
主程序:
%% 用Opt_Golden()求解最优化
f1201 = inline('x-(x.*x-2).^3/2','x');
a = 0;
b = 4;
TolX = 1e-4;%判断循环是否停止的x阈值
TolFun = 1e-4; %函数阈值
MaxIter = 100; %设定迭代次数
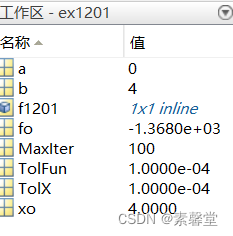
[xo,fo] = Opt_Golden(f1201,a,b,TolX,TolFun,MaxIter)
子程序:
function [xo,fo]=Opt_Golden(f,a,b,TolX,TolFun,k)
%%%%黄金搜索算法求在区间[a,b]上的最优化解
%f为目标函数,TolX为x阈值,TolFun为函数阈值,k为迭代次数
r =(sqrt(5)-1)/2; %r为黄金分割点值,
h = b-a; %区间宽度
rh = r*h;
%%%取两点c、d,并计算相应的函数值fc和fd
c = b-rh;
d = a+rh;
fc = feval(f,c);
fd = feval(f,d);
%%%算法第二步判断是否停止迭代
if k <= 0 | (abs(h) < TolX & abs(fc - fd) < TolFun)
if fc <= fd
xo = c;
fo = fc;
else
xo = d;
fo = fd;
end
if k == 0
fprintf('最好设定迭代次数大于0');
end
%%%%算法第三步,进行新一轮迭代
else
if fc < fd
[xo,fo] = Opt_Golden(f,a,d,TolX,TolFun,k-1);
else
[xo,fo] = Opt_Golden(f,c,b,TolX,TolFun,k-1);
end
end
3.运行结果

相关文章:

25、matlab里面的10中优化方法介绍——Opt_Golden法(matlab程序)
1.简述 基本思想 黄金分割法也称为 0.618 法,其基本思想是通过取试探点和进行函数值比较,使包含极小点的搜索区间不断缩短以逼近极小值点。适用于确定区间上的任何单谷函数求极小值的问题。 公式推导 设有定义在[ a , b ] [a,b][a,b]上的单谷函数 φ ( …...

点云拟合球体
前言:在很多情况下,需要根据点云来拟合球体,本博文主要介绍各种方法的拟合情况及优缺点,希望对各位小伙伴有所帮助! 目录 1. vtkFitImplicitFunction进行球拟合 2. 四点求解球 1. vtkFitImplicitFunction进行球拟合 …...
算法的增程式EV能量管理策略研究(MATLAB编程))
基于动态规划(DP)算法的增程式EV能量管理策略研究(MATLAB编程)
文章目录 算法代码仿真结果结果分析算法代码 clc; clear; close all; load CWTVC.mat N=length(T_z); %N=200;load minFuelConsup.txt minFuel_Pe=minFuelConsup(:...

前端知识点视频补充
使用工具: Vscode使用: 需要下载插件:open in browser。这个插件可以快速打开浏览器。 选择文件夹有两种方式:选择打开文件、拖拽方式(这种最方便) 快捷键:快速生成Htm结构文件:…...

python多线程—终止子线程
总体思路 1、获取需要终止的子线程id 2、根据子线程id,终止子线程。 过程 获取子线程id: import threading Thread_id threading.get_ident() # 获取子线程的id值线程终止函数 def async_raise(Thread_id, exctype):"""raises th…...

#P1012. [NOIP2015提高组] 神奇的幻方
题目描述 幻方是一种很神奇的 N \times NNN 矩阵:它由数字 1,2,3, \ldots ,N \times N1,2,3,…,NN 构成,且每行、每列及两条对角线上的数字之和都相同。 当 NN 为奇数时,我们可以通过以下方法构建一个幻方: 首先将 11 写在第一行…...
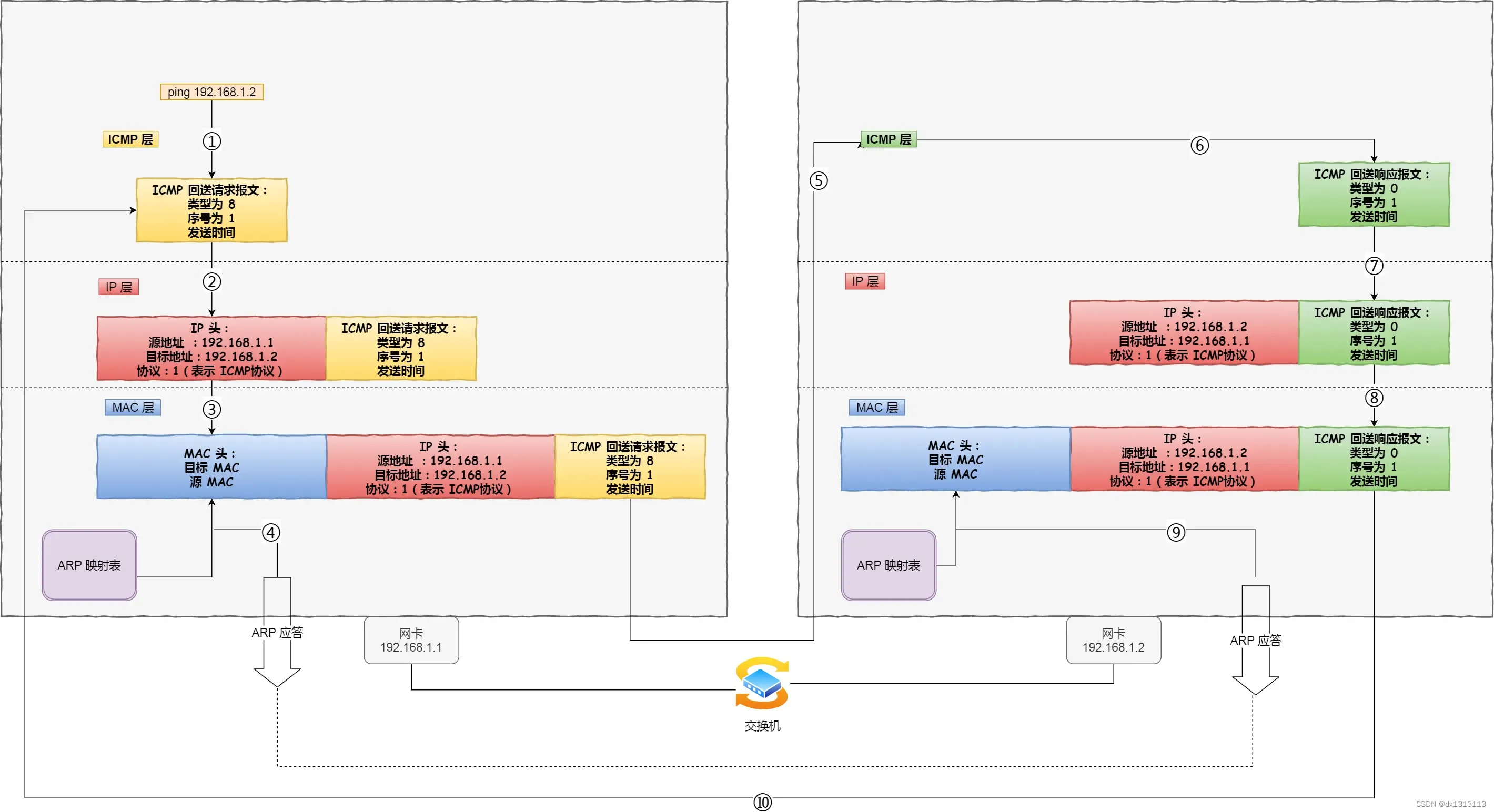
(学习笔记-IP)Ping的工作原理
Ping是基于ICMP协议工作的,ICMP报文封装在IP包里面,它工作在网络层,是IP协议的助手。 ICMP包头的类型字段,大致可分为两大类: 一类是用于诊断的查询消息,也就是查询报文类型一类是通知出错原因的错误消息&…...

php 进程间通信:管道、uds
1、管道 1.1、管道概念 管道是单向的、先进先出的,它把进程的输出和另一个进程的输入连接在一起。一个进程往管道写入数据,另一个进程从管道读取数据。数据被从管道中读取出来之后,将被删除,其他进程无法在读取到相应的数据。管…...

Stable Diffusion如何生成高质量的图-prompt写法介绍
文章目录 Stable Diffusion使用尝试下效果prompt的编写技巧prompt 和 negative promptPrompt格式Prompt规则细节优化Guidance Scale 总结 Stable Diffusion Stable Diffusion是一个开源的图像生成AI系统,由Anthropic公司开发。它基于 Transformer模型架构,可以通过文字描述生成…...

MySQL 高级SQL语句(一)
目录 一、高级SQL语句(进阶查询) 1.1 select 1.2 distinct 1.3 where 1.4 and 和 or 1.5 in 1.6 between 1.7 通配符 1.8 like 1.9 order by 一、高级SQL语句(进阶查询) 先准备2个表 一个location表: use m…...

SkyWalking链路追踪-技术文档首页
SkyWalking 文档中文版(社区提供) (skyapm.github.io)https://skyapm.github.io/document-cn-translation-of-skywalking/ SkyWalking-基本概念 SkyWalking链路追踪是一个用于分布式系统的性能监控工具,它帮助开发人员了解系统中各组件之间…...
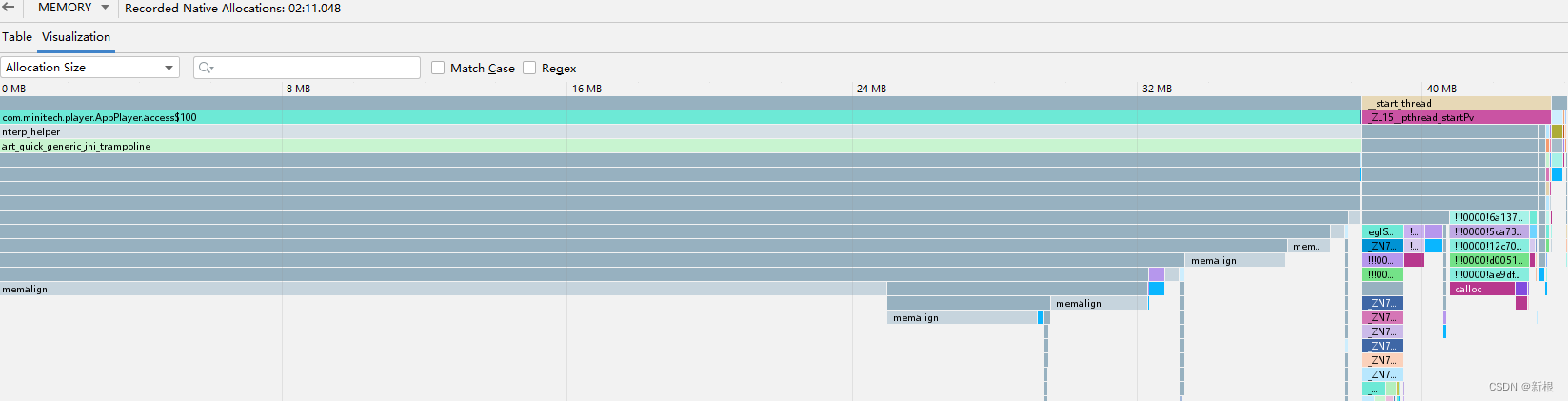
AndroidStudio Memory profiler(内存分析器)
1.Record Java/Kotlin allocations 查看java 层中对象的调用栈和短时间内创建对象的次数。可用于内存抖动快速分析,可用快速查找到该对象的调用栈(等同于mat) 从上图可见,短时间内创建了23个char[] 数组,其中最大的char[] 占用20k, 查看cll stack 调用…...

【C++模板进阶】
目录 一、模板使用时的一个小注意点二、非类型模板参数三、类模板的特化3.1函数模板的特化3.2类模板的特化3.2.1全特化3.2.2偏特化 四、模板的分离编译4.1模板不支持分离编译4.2模板分离编译报错的分析4.2解决方案 五、模板的总结 一、模板使用时的一个小注意点 在使用模板时&…...
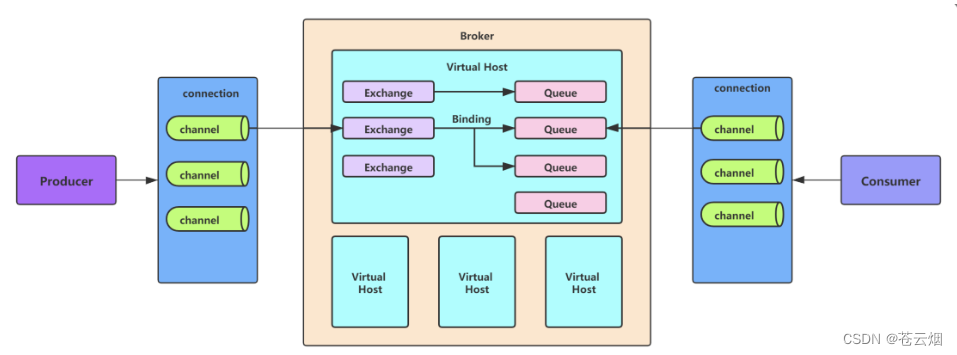
(一)RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理
Lison <dreamlison163.com>, v1.0.0, 2023.06.22 RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理 文章目录 RabbitMQ概念-优势、劣势、应用场景 、AMQP、工作原理RabbitMQ概念RabbitMQ的优势RabbitMQ劣势RabbitMQ应用的场景RabbitMQ_AMQPRabbitMQ工作原理 RabbitM…...
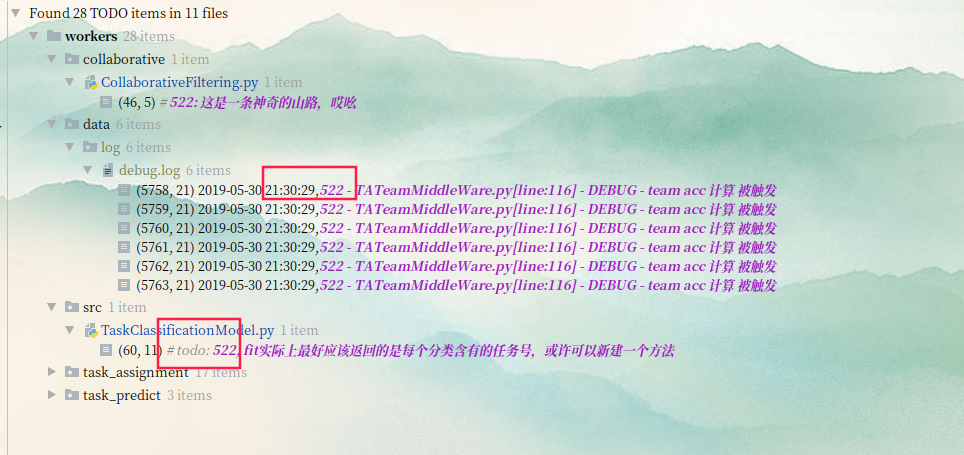
JetBrains全家桶:如何自定义实现类TODO注释?
文章目录 效果图具体方法参考文献 效果图 TODO注释大家应该都用过,在注释开头打上TODO的话,软件下方的TODO选项卡里就可以自动筛选出你打了TODO的注释,你可以点击里面对应的注释来实现快速跳转。 jetbrains全家桶(如Pycharm、Int…...

【技术干货】工业级BLE5.2蓝牙模块SKB378 使用教程,AT指令集
SKB378是一个高度集成的蓝牙5.2模组,可用来在2.4GHz ISM频段内做高速率、短距离无线通信。工业级标准,支持主从模式(1主对8从),支持串口透传,AT指令控制,且支持AoA蓝牙高精度室内定位,模组内部集成32位ARM …...
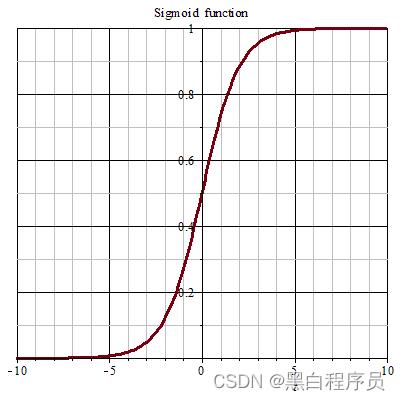
零基础深度学习——学习笔记1 (逻辑回归)
前言 因为各种各样的原因要开始学习深度学习了,跟着吴恩达老师的深度学习视频,自己总结一些知识点,以及学习中遇到的一些问题,以便记录学习轨迹以及以后复习使用,为了便于自己理解,我会将一些知识点用以个…...
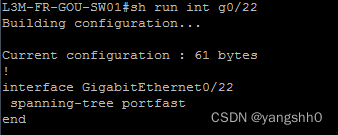
I want to know on what switchport is connected my computer (10.8.0.2)
i.e. I am connected to an L2. I want to know on what switchport is connected my computer (10.8.0.2) Well….obviously not on this switch. Let’s dig Now I have the MAC address of my computer, we confinue to dig Computer has been seen on interface g0/2. Let’…...

OpenCv之人脸操作
目录 一、马赛克实现 二、人脸马赛克 三、人脸检测 四、多张人脸检测 一、马赛克实现 案例代码如下: import cv2 import numpy as npimg cv2.imread(8.jpg) # 马赛克方式一:缩小图片 # img2 cv2.resize(img,(600,400)) # # 马赛克方式二: # img2 cv2.resize(img,(600,4…...

C++[第五章]--指针和引用
指针和引用 文章目录 指针和引用1、引用2、指针3、右值引用4、引用限定符const和引用限定符1、引用 引用就是别名,引用定义时必须初始化: int a; int &b=a; //b即为a的别名 如果不是形参,必须初始化,引用某一变量 2、指针 指针和c一样; this指针 在类的成员函数中使…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
