【动态规划】简单多状态
文章目录
- 动态规划(简单多状态)
- 1. 按摩师
- 2. 打家劫舍 ||
- 3. 删除并获得点数
- 4. 粉刷房子
- 5. 最佳买卖股票时机含冷冻期
- 6. 买卖股票的最佳时机含手续费
- 7. 买卖股票的最佳时机 |||
- 8. 买卖股票的最佳时机 IV
动态规划(简单多状态)
1. 按摩师
题目链接
-
状态表示
dp[i]表示到i位置的时候预约的最大时长。但是这个题目我们可以选择接或不接。因此可以继续划分为两个子状态:f[i]表示:到i位置时接受的最大时长g[i]表示:到i位置时不接受的最大时长
-
状态转移方程
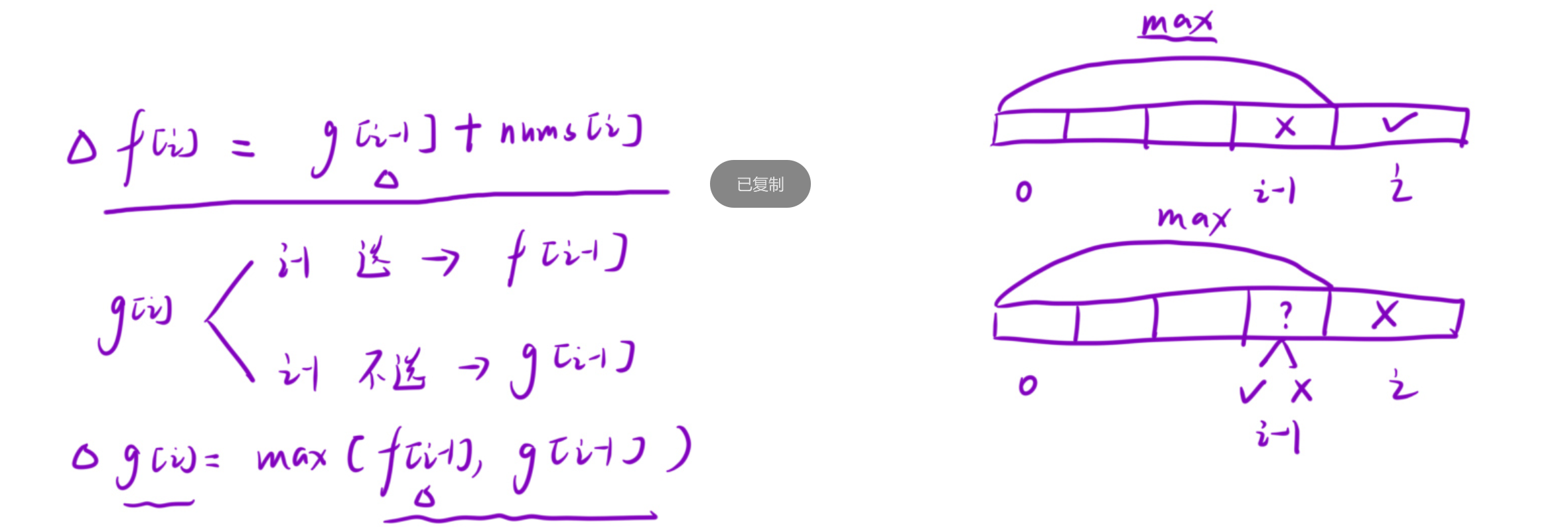
-
初始化
因为这个题目比较简单,所以不需要使用虚拟节点的方法,初始化是为了后面填表的时候不越界
f[0] = nums[0], g[0] = 0 -
填表
从左到右
-
返回值
接受最后一个或者不接受的最大值
AC代码:
class Solution
{
public:int massage(vector<int>& nums) {int n = nums.size();if (n == 0) return 0;vector<int> f(n);auto g = f;f[0] = nums[0], g[0] = 0;for (int i = 1; i < n; i++){f[i] = g[i - 1] + nums[i];g[i] = max(f[i - 1], g[i - 1]);}return max(f[n - 1], g[n - 1]);}
};
2. 打家劫舍 ||
题目链接
分析:
由于房间是连续的,也就是一个环,因此可以分类讨论:
- 偷第一个时,第二个和最后一个不能偷
- 不偷第一个,可以偷第二个和最后一个
因此只需要两种情况的最大值就可以
-
状态表示
dp[i]表示偷到i时的最大金额,但是依然可以划分为两种情况偷或不偷f[i]表示偷i时的最大金额g[i]表示不偷i时的最大金额 -
状态转移方程

-
初始化
保证后续的填表不越界
-
填表
从左到右,两个一起填
-
返回值
最大值
AC代码:
class Solution
{
public:int rob(vector<int>& nums) {int x = 0, y = 0;int n = nums.size();x += nums[0];x += recursion(2, n - 2, nums);y += recursion(1, n - 1, nums);return max(x, y);}int recursion(int left, int right, vector<int> &v){if (left > right) return 0;int n = v.size();vector<int> f(n);auto g = f;f[left] = v[left]; // 初始化for (int i = left + 1; i <= right; i++){f[i] = g[i - 1] + v[i];g[i] = max(g[i - 1], f[i - 1]);}return max(f[right], g[right]);}
};
3. 删除并获得点数
题目链接
分析:我们把所有数字的点数之和,放到一个数组当中,在进行一次打家劫舍就可以了
把原数组转换成一个新数组,新数组的下标i所对应的值为原数组的元素i在原数组中数字的总和,比如原数组[2, 2, 3, 3, 3, 4],转换为新数组就是[0, 0, 4, 9, 4]。在新数组中,下标0和1表示在原数组中没有0和1这两个数,新数组下标2的值是4,表示在原数组中,所有2的总和是4。转换的目的就是可以从新数组中得到删除nums[i]而得到的点数,也就是可以打劫的金额。因为删除nums[i]后,还要删除nums[i] + 1和nums[i] - 1,在新数组中就意味着不能取相邻的元素,不能取相邻的元素和打家劫舍也是一样的。接下来就可以使用打家劫舍的方式解答了
AC代码:
class Solution
{
public:const int N = 10001;int deleteAndEarn(vector<int>& nums) {vector<int> arr(N);for (auto e : nums) arr[e] += e;vector<int> g(N);auto f = g;for (int i = 1; i < N; i++){f[i] = g[i - 1] + arr[i];g[i] = max(g[i - 1], f[i - 1]);}return max(g[N - 1], f[N - 1]);}
};
4. 粉刷房子
题目链接
-
状态表示
dp[i]表示到i时,所需的最少费用。但是到i的时候可以有三种情况我们需要分三个子状态dp[i][0], dp[i][1], dp[i][2] -
状态转移方程

-
初始化
采用虚拟节点的方式
-
填表
-
返回值
返回三个表中的最小值
AC代码:
class Solution
{
public:int minCost(vector<vector<int>>& costs) {// 0: 红色 1:蓝色 2:绿色int n = costs.size();vector<vector<int>> dp(n + 1, vector<int>(3));for (int i = 1; i <= n; i++){dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + costs[i - 1][0];dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + costs[i - 1][1];dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + costs[i - 1][2];}int ret = INT_MAX;for (int i = 0; i < 3; i++){ret = min(ret, dp[n][i]);}return ret;}
};
5. 最佳买卖股票时机含冷冻期
题目链接
-
状态表示
dp[i]表示到i位置时的最大利润,但是到达i位置的时候仍然有3种子状态dp[i][0],表示i过后处于买入状态dp[i][1], 表示i过后处于可交易状态dp[i][2],表示i过后处于冷冻期状态
-
状态转移方程
像这种状态之间可以相互转换的,我们可以采用如下方法分析:
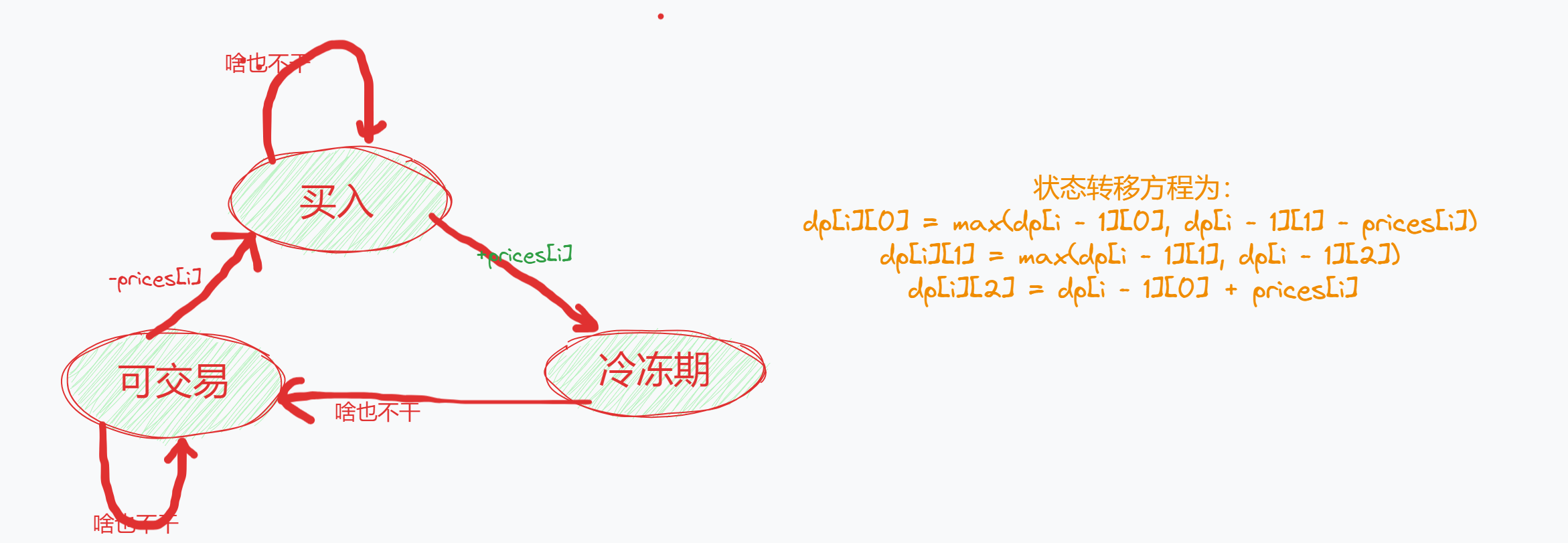
-
初始化
dp[0][0] = -prices[0], dp[0][1] = 0, dp[0][2] = 0 -
填表
三张表同时填
-
返回值
返回三中状态最后的最大值
AC代码:
class Solution
{
public:int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(3));dp[0][0] = -prices[0];for (int i = 1; i < n; i++){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);dp[i][2] = dp[i - 1][0] + prices[i];}return max(max(dp[n - 1][0], dp[n - 1][1]), dp[n - 1][2]);}
};
6. 买卖股票的最佳时机含手续费
题目链接
-
状态表示
dp[i]表示到i位置的时候,最大的利润但是到i位置的时候是有两种状态的dp[i][0]:表示是买入状态dp[i][1]表示卖出状态 -
状态转移方程
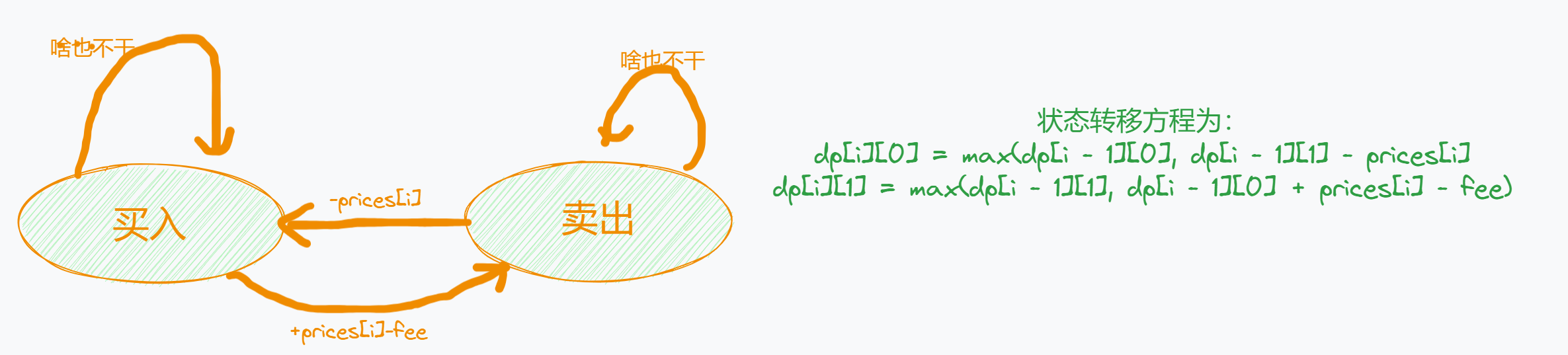
-
初始化
刚开始如果是买入状态
dp[0][0] = -prices[0] -
填表
-
返回值
AC代码:
class Solution
{
public:int maxProfit(vector<int>& prices, int fee) {int n = prices.size();vector<vector<int>> dp(n, vector<int>(2));dp[0][0] = -prices[0];for (int i = 1; i < n; i++){dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);}return max(dp[n - 1][0], dp[n - 1][1]);}
};
7. 买卖股票的最佳时机 |||
题目链接
-
状态表示
dp[i]表示到i位置的最大利润,但是还分为几个状态f[i][j]表示到i是第j次买入的最大利润g[i][j]表示到i是第j次买入的最大利润 -
状态转移方程
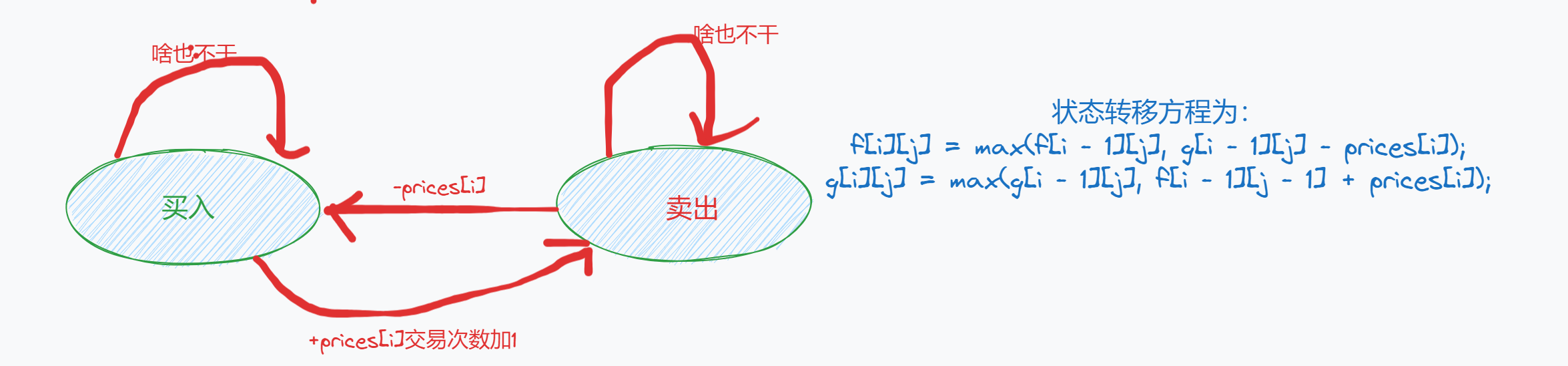
-
初始化
f[0][0] = -prices[0], g[0][0] = 0 -
填表
从上往下,每一行从左到右
-
返回值
卖出状态最后的几个中的最大值
AC代码:
class Solution
{
public:const int N = 0x3f3f3f3f;int maxProfit(vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n, vector<int>(3, -N));auto g = f;f[0][0] = -prices[0], g[0][0] = 0;for (int i = 1; i < n; i++){for (int j = 0; j < 3; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if (j - 1 >= 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for (int i = 0; i < 3; i++){ret = max(ret, g[n - 1][i]);}return ret;}
};
8. 买卖股票的最佳时机 IV
题目链接
-
状态表示
还是分为两个子状态
f[i][j]表示到i位置买入状态第j次买股票的最大利润g[i][j]表示到i位置卖出状态第j次买股票的最大利润 -
状态转移方程
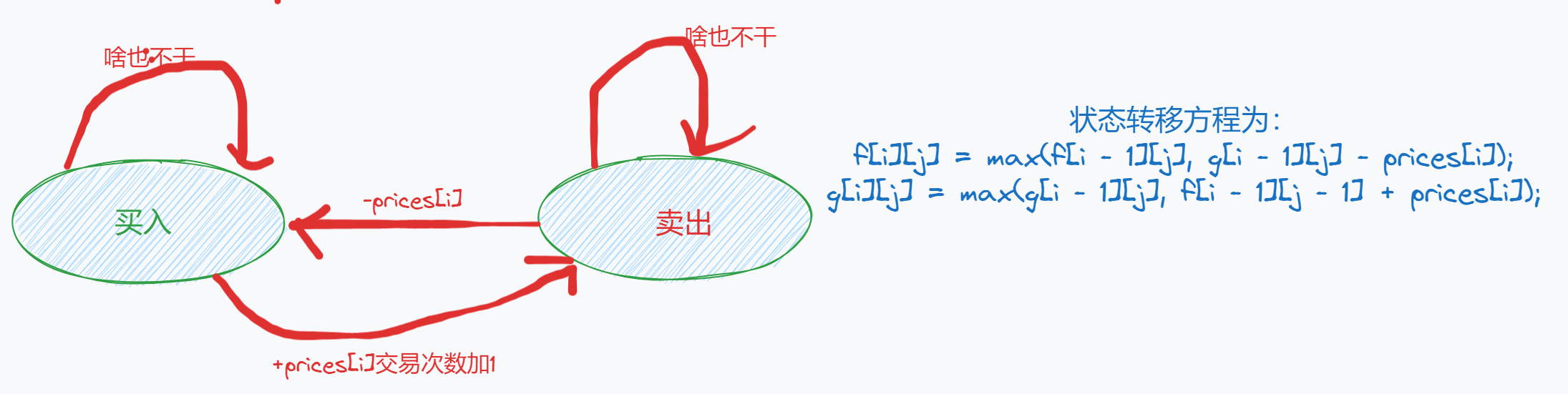
-
初始化
f[0][0] = -prices[0], g[0][0] = 0 -
填表
从上到下,从左到右
-
返回值
返回所有行的最大值
AC代码:
class Solution {
public:const int N = 0x3f3f3f3f;int maxProfit(int k, vector<int>& prices) {int n = prices.size();vector<vector<int>> f(n, vector<int>(k + 1, -N));auto g = f;f[0][0] = -prices[0], g[0][0] = 0;for (int i = 1; i < n; i++){for (int j = 0; j <= k; j++){f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);g[i][j] = g[i - 1][j];if (j - 1 >= 0) g[i][j] = max(g[i][j], f[i - 1][j - 1] + prices[i]);}}int ret = 0;for (int i = 0; i <= k; i++){ret = max(ret, g[n - 1][i]);}return ret;}
};
相关文章:

【动态规划】简单多状态
文章目录 动态规划(简单多状态)1. 按摩师2. 打家劫舍 ||3. 删除并获得点数4. 粉刷房子5. 最佳买卖股票时机含冷冻期6. 买卖股票的最佳时机含手续费7. 买卖股票的最佳时机 |||8. 买卖股票的最佳时机 IV 动态规划(简单多状态) 1. 按…...

科技资讯|苹果计划本月推出Vision Pro头显开发套件,电池有重大更新
根据消息源 aaronp613 分享的信息,苹果计划本月底面向开发者,发布 Vision Pro 头显开发套件。消息源还指出苹果更新了 Vision Pro 头显电池组的代号,共有 A2781,A2988 和 A2697 三种不同的型号,目前尚不清楚三者之间的…...

k8s 将pod节点上的文件拷贝到本地
要将 Kubernetes(k8s)中 Pod 节点上的文件拷贝到本地,可以通过使用 kubectl cp 命令来实现。kubectl cp 命令允许你在本地系统和 Pod 之间复制文件和目录。 下面是使用 kubectl cp 命令的语法: kubectl cp <namespace>/&l…...

Git简介与工作原理:了解Git的基本概念、版本控制系统和分布式版本控制的工作原理
🌷🍁 博主 libin9iOak带您 Go to New World.✨🍁 🦄 个人主页——libin9iOak的博客🎐 🐳 《面试题大全》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~ἳ…...

java篇 类的进阶0x02:方法重载
文章目录 方法重载 overload方法签名返回值不属于方法签名的原因: 重载的参数匹配规则 方法重载 overload 多个方法功能很相似,但不完全一样,可以考虑使用方法的重载。 同一个类中,方法可以重名,但是签名不可以重复。…...

Android11 相机拍照权限,以及解决resolveActivity返回null
一、配置拍照和读写权限 <uses-permission android:name"android.permission.CAMERA"/> <uses-feature android:name"android.hardware.camera" /><uses-permission android:name"android.permission.WRITE_EXTERNAL_STORAGE"/&…...
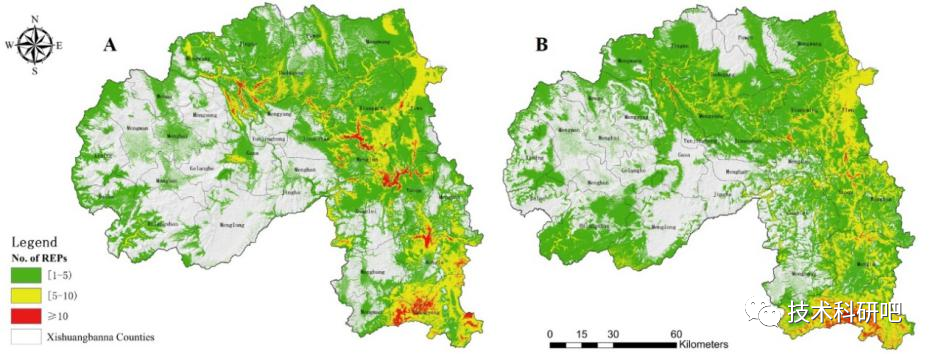
MAXENT模型的生物多样性教程
详情点击链接:基于MAXENT模型的生物多样性生境模拟与保护优先区甄选、自然保护区布局优化及未来气候变化下评估中的应用及论文写作 一:生物多样性保护格局与自然保护区格局优化 1.我国生物多样性格局与分布; 2.我国自然保护区格局与分布&…...
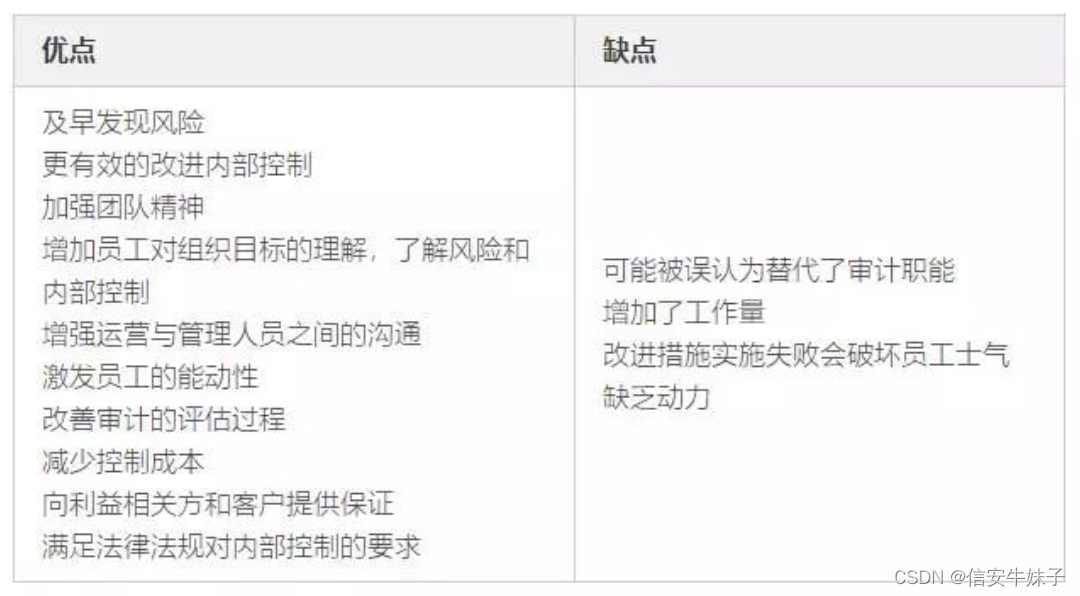
CISA学习笔记-第一章、信息系统审计过程
传统的审计三方关系理论指明,审计作为独立于会计记录之外的一项重要职能,是公司财务信息公允可靠的有力保障,制约着会计行为,制衡了会计权力。 1. IS审计和保障标准、指南、工具 职业道德规范 信息技术保证框架(ITAF&a…...
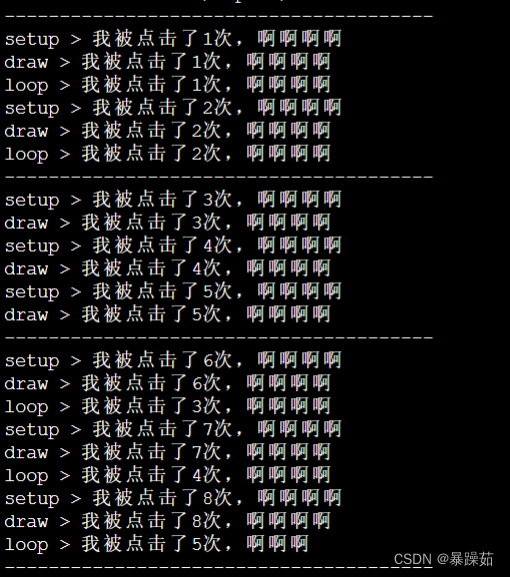
回调函数的使用:案例一:c语言简单信号与槽机制。
系列文章目录 文章目录 系列文章目录前言一、回调函数1.1 回调函数基本概念1.2 简单实现 二、代码案例1.代码示例 总结 前言 了解回调函数的基本概念,函数指针的使用、简单信号与槽的实现机制; 一、回调函数 1.1 回调函数基本概念 回调函数就是一个通…...

python matplotlib库 设置字体字号等
主要是记录字体、字号对应的参数。注意字符串类型的参数要加引号 1.字体: fontname 常见参数: # 常用 Times New Roman、Dejavu sans、TeX Gyre Schola中文字体 黑体:SimHei 微软雅黑:Microsoft YaHei 微软正黑体:M…...
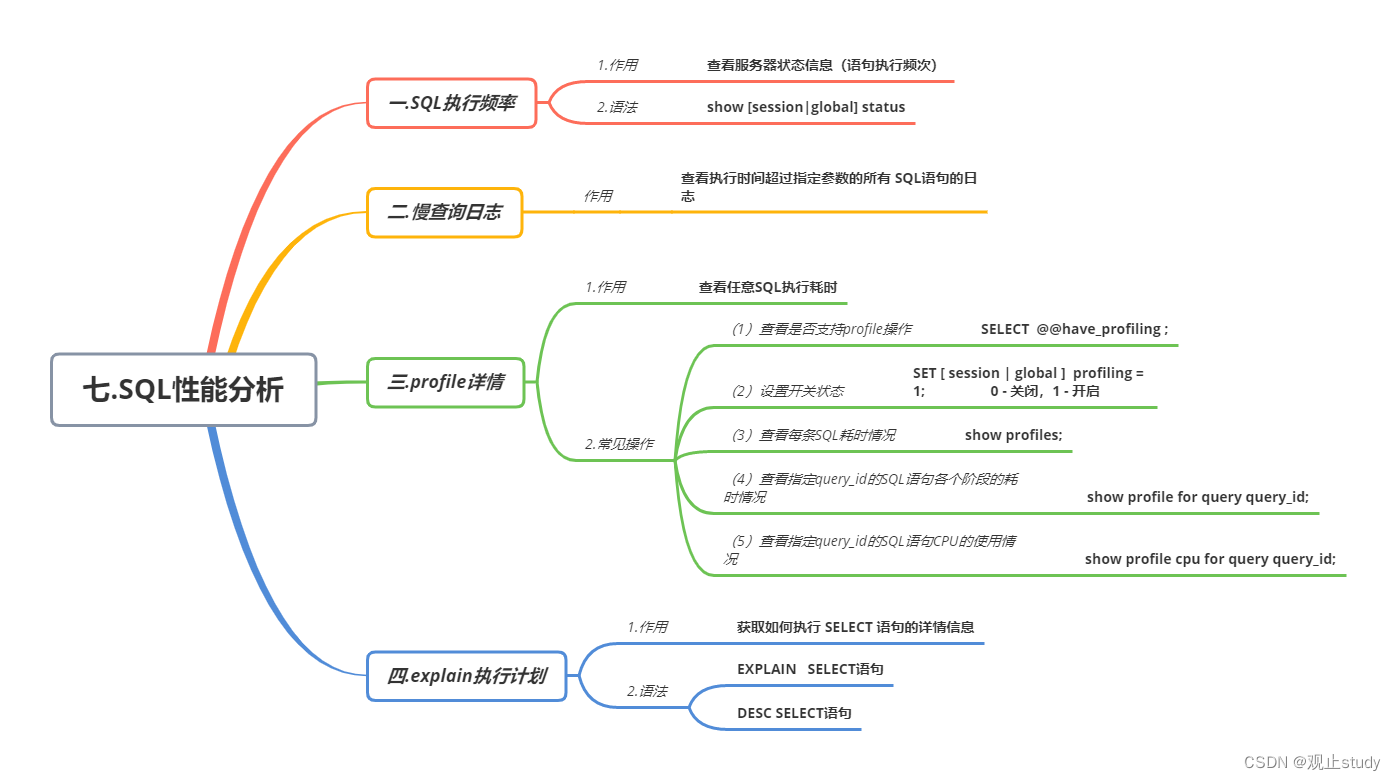
【MySQL】SQL性能分析 (七)
🚗MySQL学习第七站~ 🚩本文已收录至专栏:MySQL通关路 ❤️文末附全文思维导图,感谢各位点赞收藏支持~ 假如我们需要对SQL进行优化,我们就必须对他足够的了解,比如 对哪一类SQL进行优化(增删改查…...

超越想象的GPT医疗 20230723
7月份读完了这本书,趁着周末写下读书笔记吧 这本书 作者:【美】彼得.李 Peter Lee 【美】凯丽.戈德伯格CareyGoldberg 著 【美】伊萨克.科恩Isaac Kohane 芦义 译 在AI风起云涌时代,在这刚刚过去的新冠三年,“超越想象的GPT医…...

【N32L40X】学习笔记03-gpio输出库
gpio输出 该函数库的目的就是在统一的地方配置,将配置的不同项放置在一个结构体内部使用一个枚举来定义一个的别名 led.c #include <stdio.h> #include "led/bsp_led.h"static led_t leds[LED_NUM]{{GPIOB,GPIO_PIN_2,RCC_APB2_PERIPH_GPIOB},{GP…...
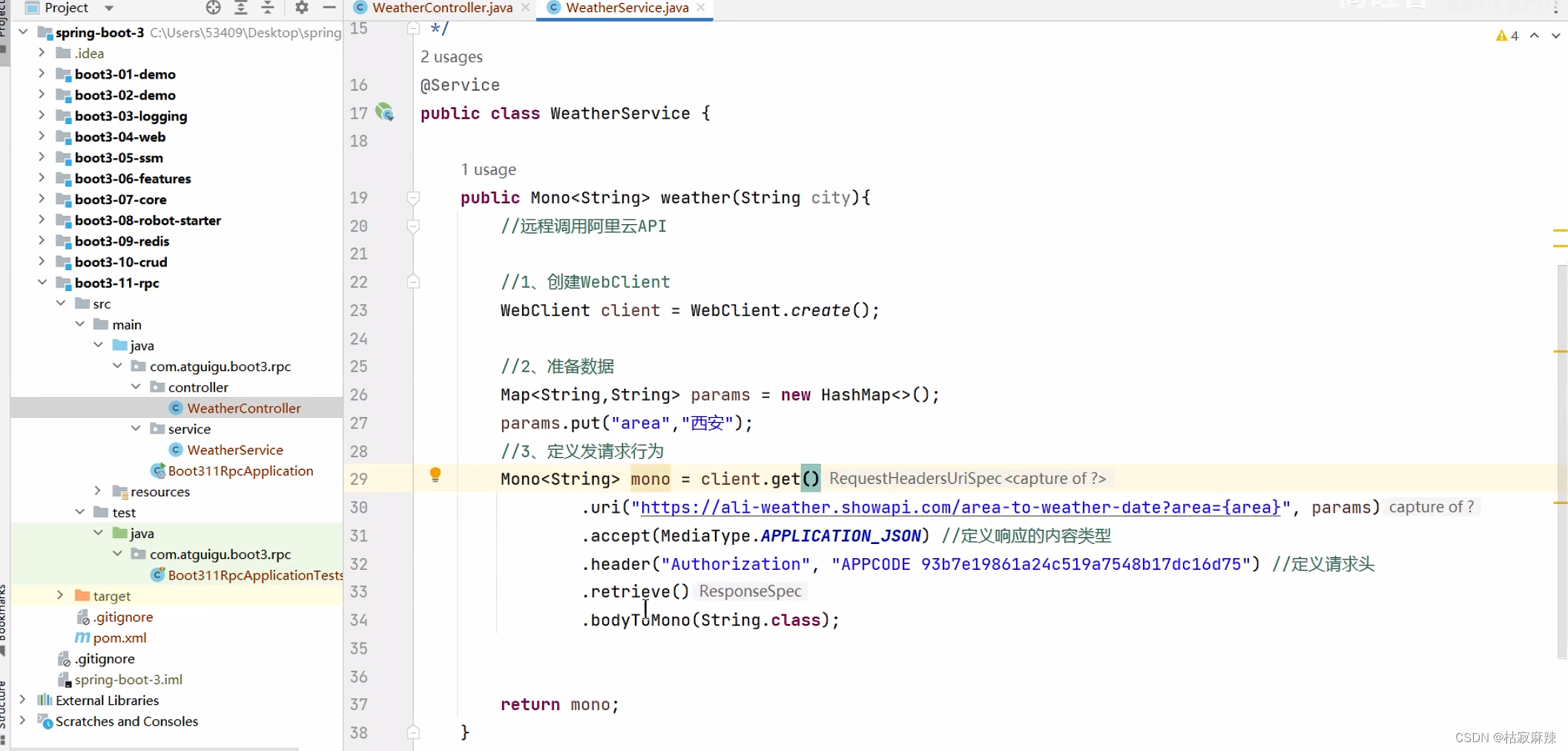
WebClient,HTTP Interface远程调用阿里云API
HTTP Interface Spring 允许我们通过定义接口的方式,给任意位置发送 http 请求,实现远程调用,可以用来简化 HTTP 远程访问。需要webflux场景才可 <dependency><groupId>org.springframework.boot</groupId><artifactId&…...
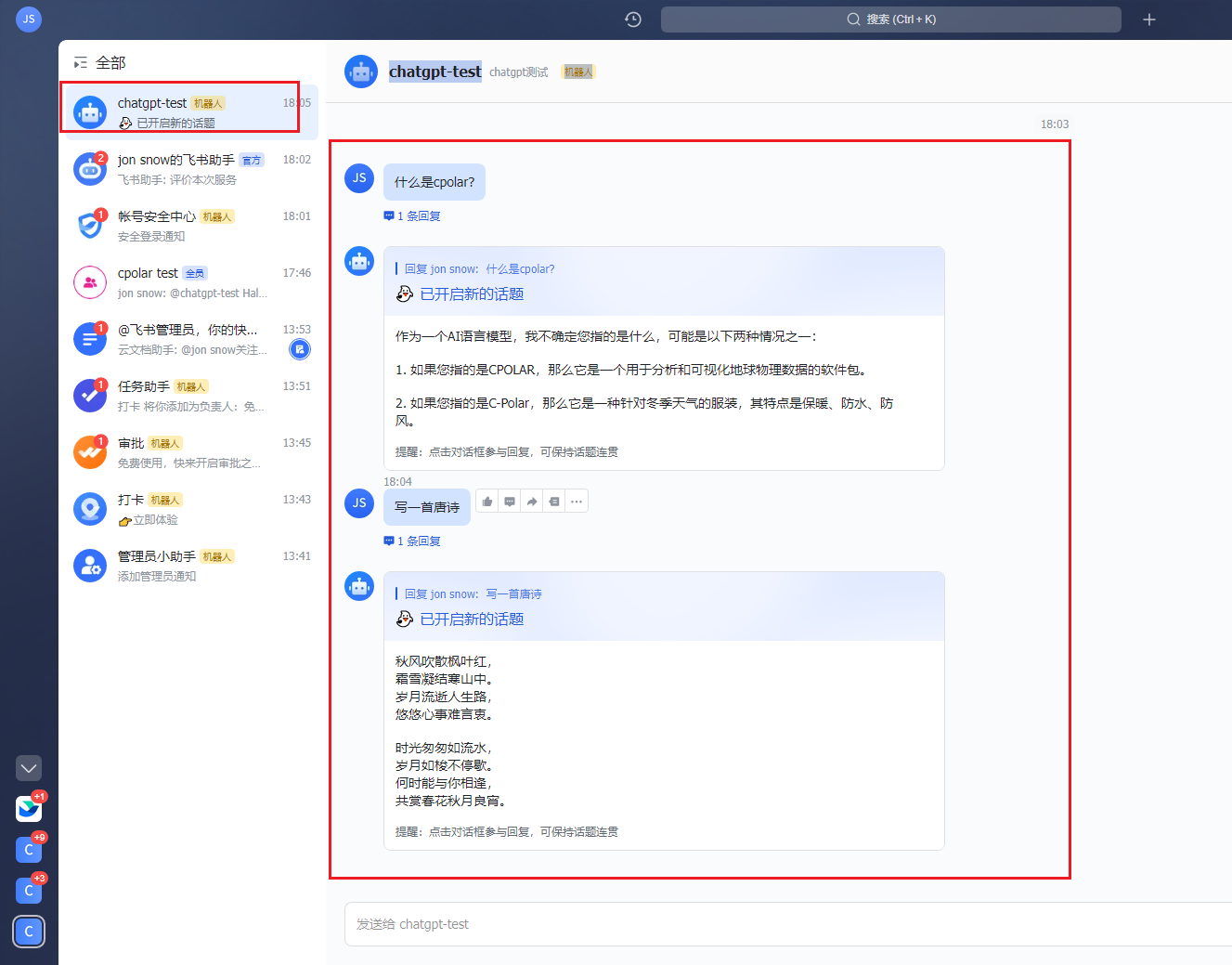
飞书ChatGPT机器人 – 打造智能问答助手实现无障碍交流
文章目录 前言环境列表1.飞书设置2.克隆feishu-chatgpt项目3.配置config.yaml文件4.运行feishu-chatgpt项目5.安装cpolar内网穿透6.固定公网地址7.机器人权限配置8.创建版本9.创建测试企业10. 机器人测试 前言 在飞书中创建chatGPT机器人并且对话,在下面操作步骤中…...

React、Vue框架如何实现组件更新,原理是什么?
引言 React 和 Vue 都是当今最流行的前端框架,它们都实现了组件化开发模式。为了优化性能,两者都采用了虚拟DOM技术。当组件状态发生改变时,它们会使用虚拟DOM进行局部渲染比对,只更新必要的DOM节点,从而避免重新渲染整个组件树。本文将从React和Vue的组件更新原理入手,剖析两…...

常见面试题之设计模式--策略模式
1. 概述 先看下面的图片,我们去旅游选择出行模式有很多种,可以骑自行车、可以坐汽车、可以坐火车、可以坐飞机。 作为一个程序猿,开发需要选择一款开发工具,当然可以进行代码开发的工具有很多,可以选择Idea进行开发&a…...

redis多key问题
多key问题指的是在Redis中存在大量的key,如果这些key过多,超过了Redis可以容纳的内存大小,那么数据会被保存在交换空间(swap区),这会导致性能下降。 Redis是一种基于内存的缓存数据库,它的性能…...
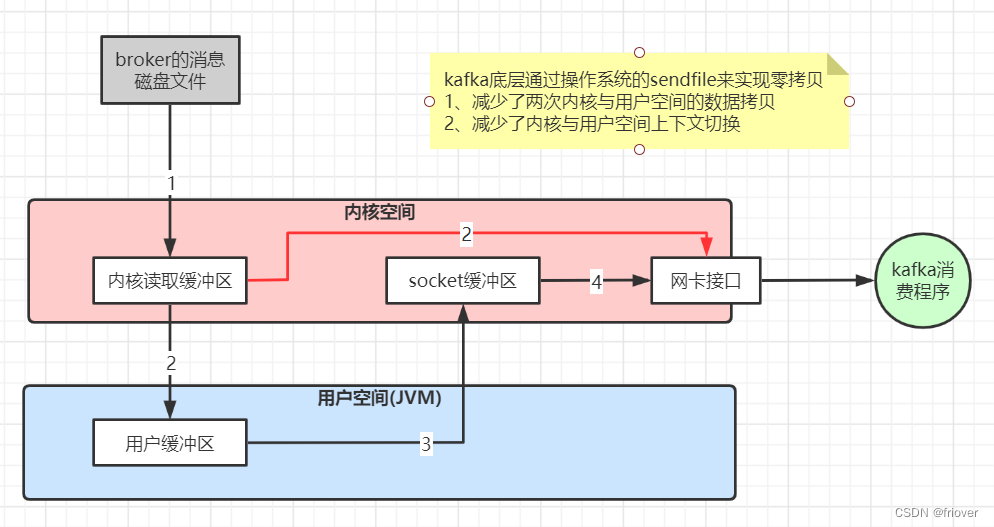
kafka第三课-可视化工具、生产环境问题总结以及性能优化
一、可视化工具 https://pan.baidu.com/s/1qYifoa4 密码:el4o 下载解压之后,编辑该文件,修改zookeeper地址,也就是kafka注册的zookeeper的地址,如果是zookeeper集群,以逗号分开 vi conf/application.conf 启…...

2_Apollo4BlueLite中断控制器NVIC
1.概述 Apollo4BlueLite 的中断控制器是采用 ARM Cortex-M4 内核,并集成了 NVIC(Nested Vectored Interrupt Controller,嵌套向量中断控制器)作为其中断控制器。 NVIC 是 ARM Cortex-M 系列处理器中常用的中断控制器,…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
