二叉树详解
这里写目录标题
- 前言
- 树型结构(了解)
- 树常见的概念
- 树的表示形式(了解)
- 树的应用
- 二叉树
- 概念
- 两种特殊的二叉树
- 二叉树的性质(重要)
- 二叉树的存储
- 二叉树的基本操作
前言
本篇博客讲述了以下几个知识点
- 树的基本概念
- 二叉树概念及特性
- 二叉树的基本操作
树型结构(了解)
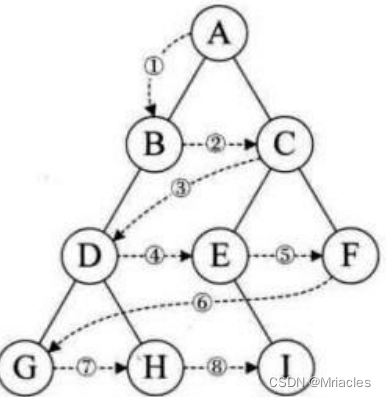
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点
- 有一个特殊的结点,称为根结点,根结点没有前驱结点除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm,其中每一个集合Ti (1 <= i <=m) 又是一棵与树类似的子树。
- 每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的。
树的图片
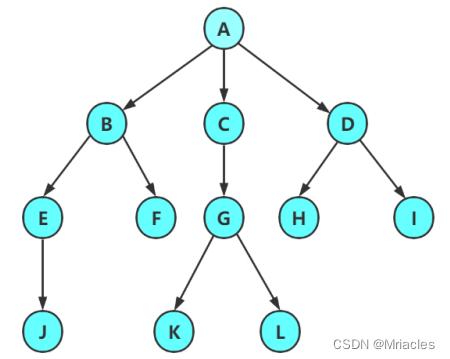
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
树常见的概念
- 结点的度:一个结点含有子树的个数称为该结点的度;
- 树的度:一棵树中,所有结点度的最大值称为树的度;
- 叶子结点或终端结点:度为0的结点称为叶结点;
- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点;
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点;
- 根结点:一棵树中,没有双亲结点的结点;
- 树的高度或深度:树中结点的最大层次;
- 非终端结点或分支结点:度不为0的结点;
- 兄弟结点:具有相同父结点的结点互称为兄弟结点;
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟;
- 结点的祖先:从根到该结点所经分支上的所有结点;
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
树的表示形式(了解)
实际中树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。最常用的是孩子兄弟表示法
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}
树的应用
文件系统管理(目录和文件)
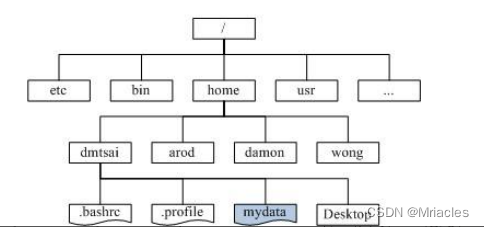
二叉树
概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成
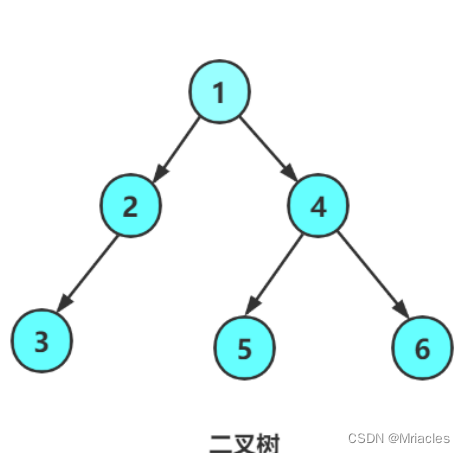
从上图可以看出: - 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
两种特殊的二叉树
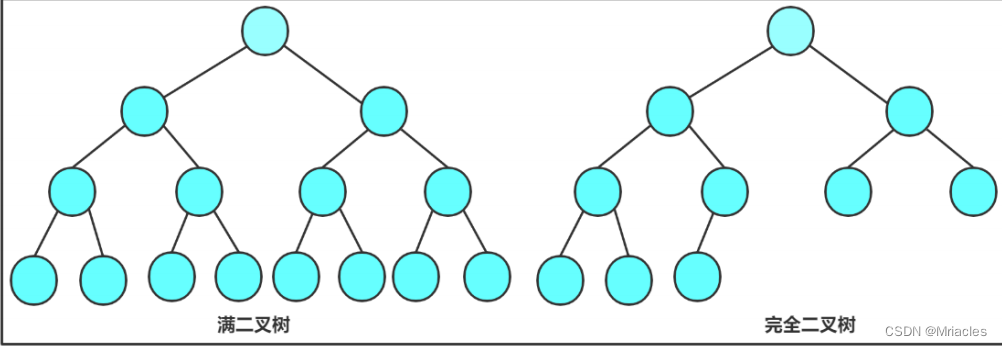
- 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
- 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
二叉树的性质(重要)
- 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 (i>0)个结点
- 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 (k>=0)
- 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
- 具有n个结点的完全二叉树的深度k为 上取整
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
若2i+1<n,左孩子序号:2i+1,否则无左孩子
若2i+2<n,右孩子序号:2i+2,否则无右孩子
二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}
二叉树的基本操作
- 前中后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
在遍历二叉树时,如果没有进行某种约定,每个人都按照自己的方式遍历,得出的结果就比较混乱,如果按照某种规则进行约定,则每个人对于同一棵树的遍历结果肯定是相同的。如果N代表根节点,L代表根节点的
左子树,R代表根节点的右子树,则根据遍历根节点的先后次序有以下遍历方式:
NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点—>根的左子树—>根的右子树。
LNR:中序遍历(Inorder Traversal)——根的左子树—>根节点—>根的右子树。
LRN:后序遍历(Postorder Traversal)——根的左子树—>根的右子树—>根节点
- 层序遍历
层序遍历:除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
相关文章:

二叉树详解
这里写目录标题 前言树型结构(了解)树常见的概念树的表示形式(了解)树的应用 二叉树概念两种特殊的二叉树二叉树的性质(重要)二叉树的存储二叉树的基本操作 前言 本篇博客讲述了以下几个知识点 树的基本概念二叉树概念及特性二叉树的基本操作 树型结构…...

Git的核心概念:探索Git中的提交、分支、合并、标签等核心概念,深入理解其作用和使用方法
🌷🍁 博主 libin9iOak带您 Go to New World.✨🍁 🦄 个人主页——libin9iOak的博客🎐 🐳 《面试题大全》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~ἳ…...
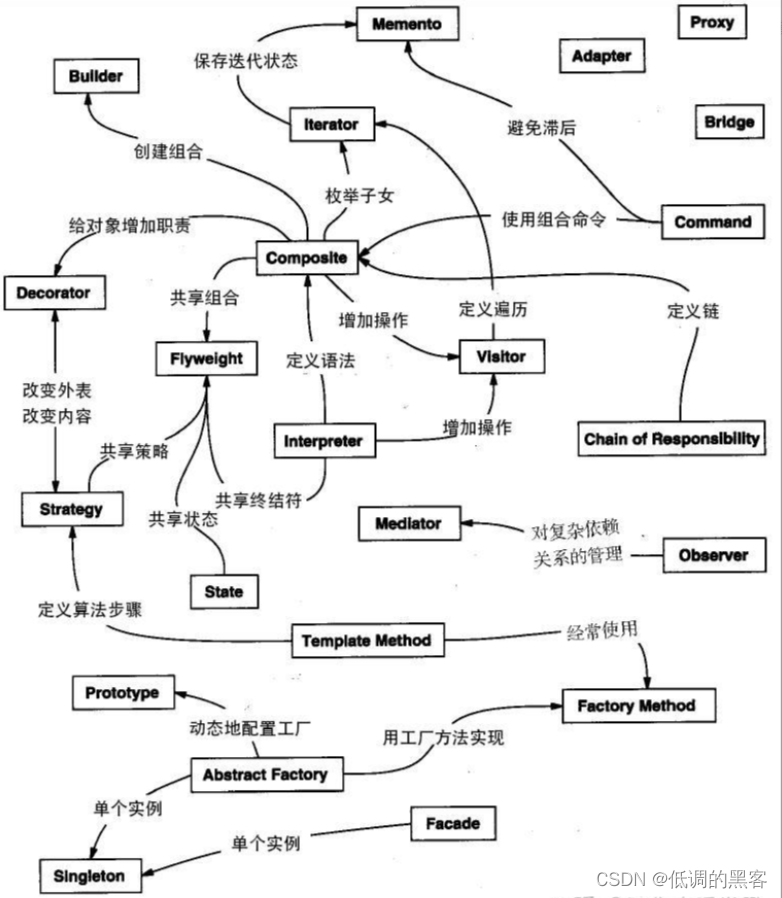
JAVA设计模式——23种设计模式详解
一、什么是设计模式🍉 设计模式(Design pattern) 是解决软件开发某些特定问题而提出的一些解决方案也可以理解成解决问题的一些思路。通过设计模式可以帮助我们增强代码的可重用性、可扩充性、 可维护性、灵活性好。我们使用设计模式最终的目…...
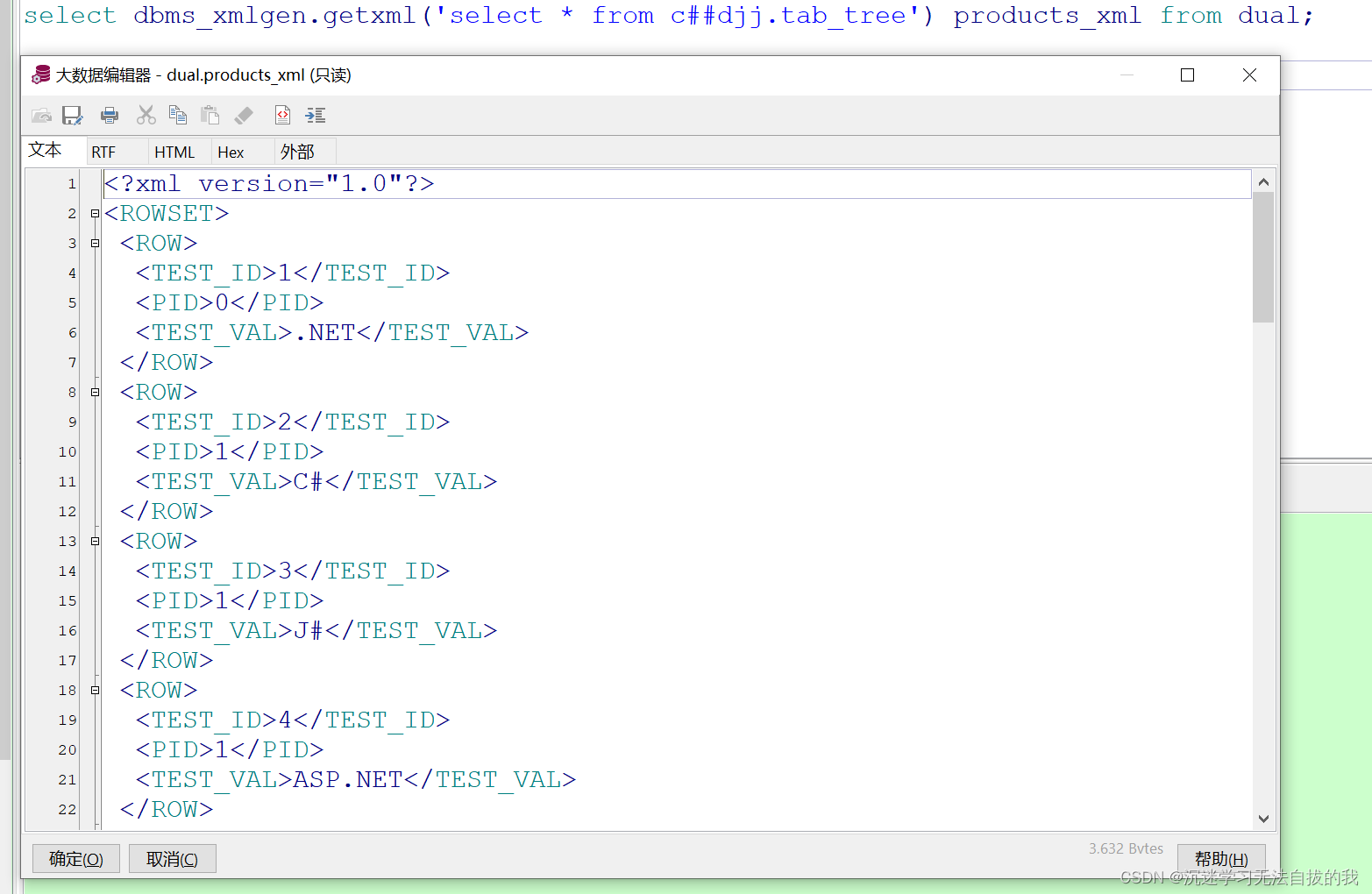
Oracle输出文本平面(CSV、XML)文本数据详细过程
此过程是提供给前端,调用的接口,为报表提供”下载“功能。以下是本人在测试环境的测试,有什么不足的地方,请留言指教,谢谢。 1、测试表 分别对测试表输出csv、xml两种格式文件数据。前期的准备工作。 --在服务器端创建directory,用管理员用户 create or replace directo…...
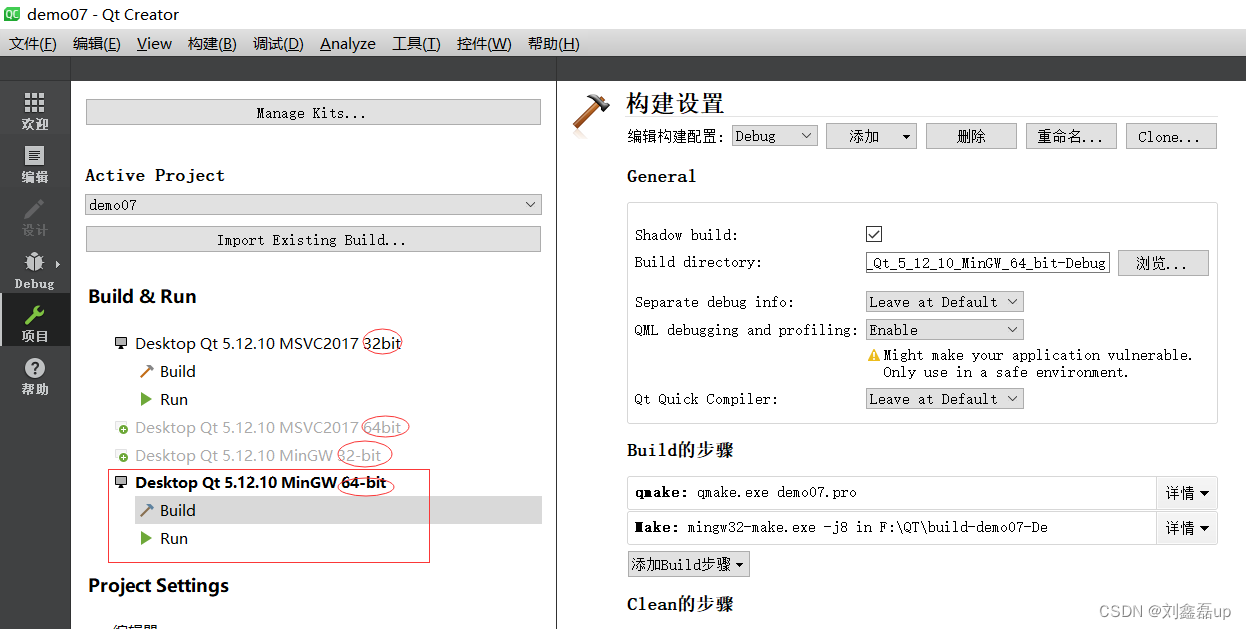
基于C++的QT基础教程学习笔记
文章目录: 来源 教程社区 一:QT下载安装 二:注意事项 1.在哪里写程序 2.如何看手册 3.技巧 三:常用函数 1.窗口 2.相关 3.按钮 4.信号与槽函数 5.常用栏 菜单栏 工具栏 状态栏 6.铆接部件 7.文本编辑 8…...
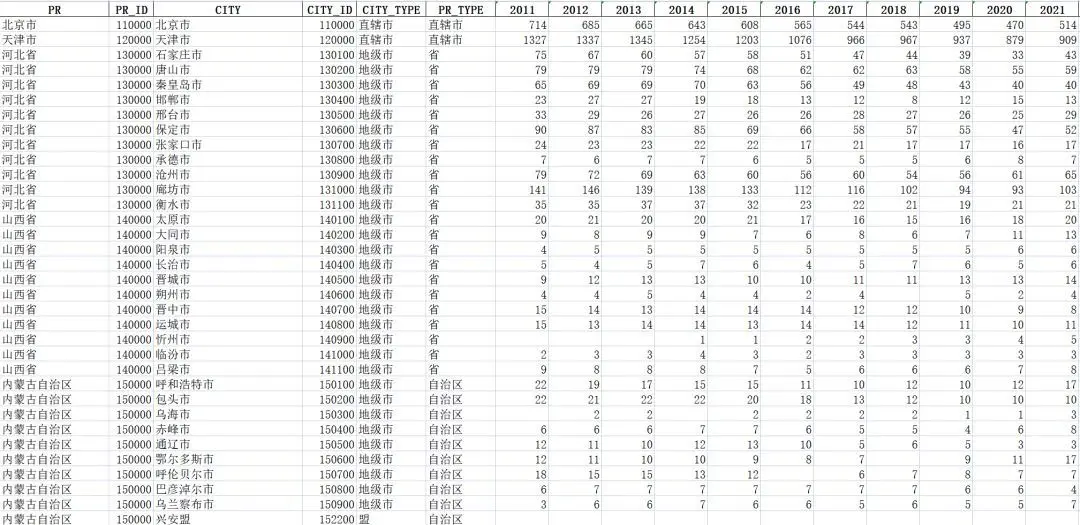
【数据分享】全国地级市1999—2020年工业企业数(Shp/Excel格式)
在之前的文章中,我们分享过基于2000-2022年《中国城市统计年鉴》整理的1999-2021年地级市的人口相关数据、各类用地面积数据、污染物排放和环境治理相关数据、房地产投资情况和商品房销售面积、社会消费品零售总额和年末金融机构存贷款余额(可查看之前的…...

设计模式【行为型】-- 责任链模式
责任链模式(Chain of Responsibility Pattern)是一种行为型设计模式,它允许多个对象依次处理同一个请求,形成一条责任链。当客户端提交一个请求时,请求沿着责任链传递,直到有一个处理者能够处理该请求为止。…...
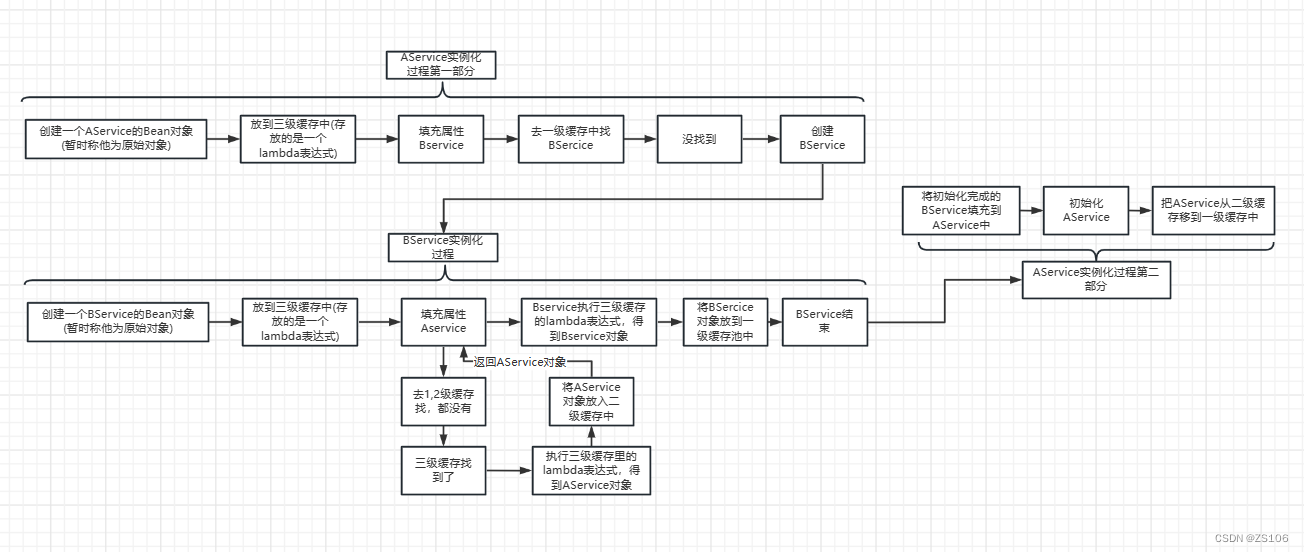
[Spring] 三级缓存解决循环依赖详解
什么是循环依赖 注册一个bean对象的过程: Spring扫描class得到BeanDefinition – 根据得到的BeanDefinition去生成bean – 现根据class推断构造方法 – 根据推断出来的构造方法,反射,得到一个对象 – 填充初始对象中的属性(依赖注入) – 如果…...
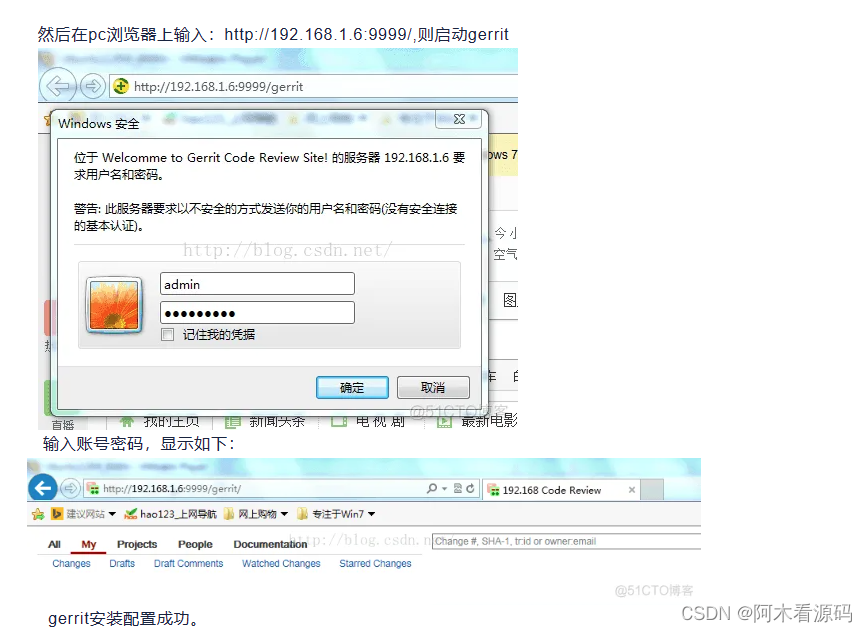
gerrit 从安装到出坑
一般公司在做代码审核的时候选择codereview gerrit来处理代码的入库的问题。 它是通过提交的时候产生Change-Id: If4e0107f3bd7c5df9e2dc72ee4beb187b07151b9 来决定是不是入库,一般如果不是通过这个管理,那么就是我们通常的操作 git add . git comm…...

Java工程师就业前景怎么样?能拿多少工资?
Java软件工程师是指运用Java这个开发工具去完成软件产品的软件程序设计、开发、测试、维护升级等工作的人员。Java程序员可以分为初级、中级、高级、资深等。不同级别的Java程序员,薪资也不一样。 Java除了一般的编程,还可以开发游戏、进行桌面设计、Ja…...
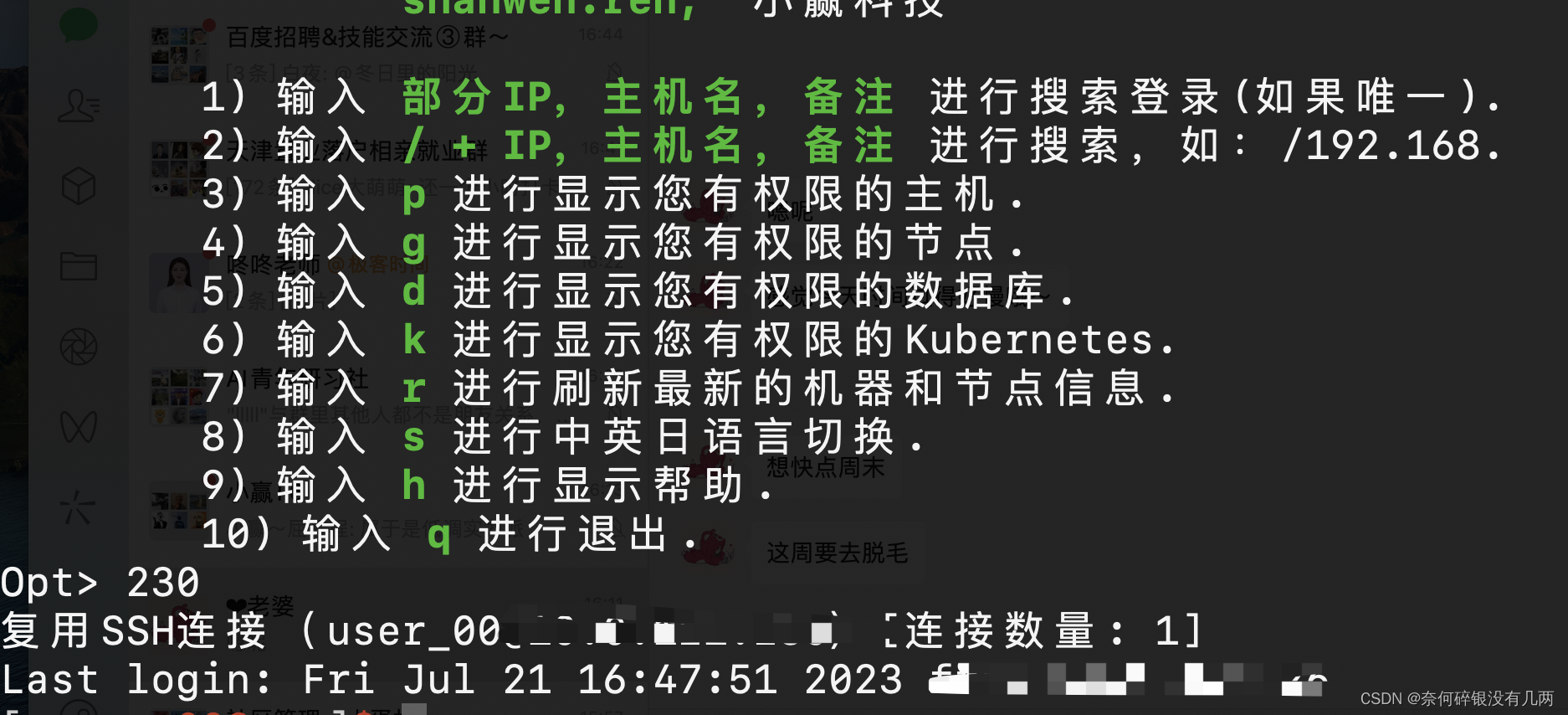
极速跳板机登陆服务器
目录 一:简单登陆跳板器二:一键申请相关的服务器权限三:简化登陆 一:简单登陆跳板器 登陆公司提供的网址, 下载自己的专属RSA密钥。在密钥文件处, 执行登陆指令: ssh -p 36000 -i id_rsa 用户跳…...
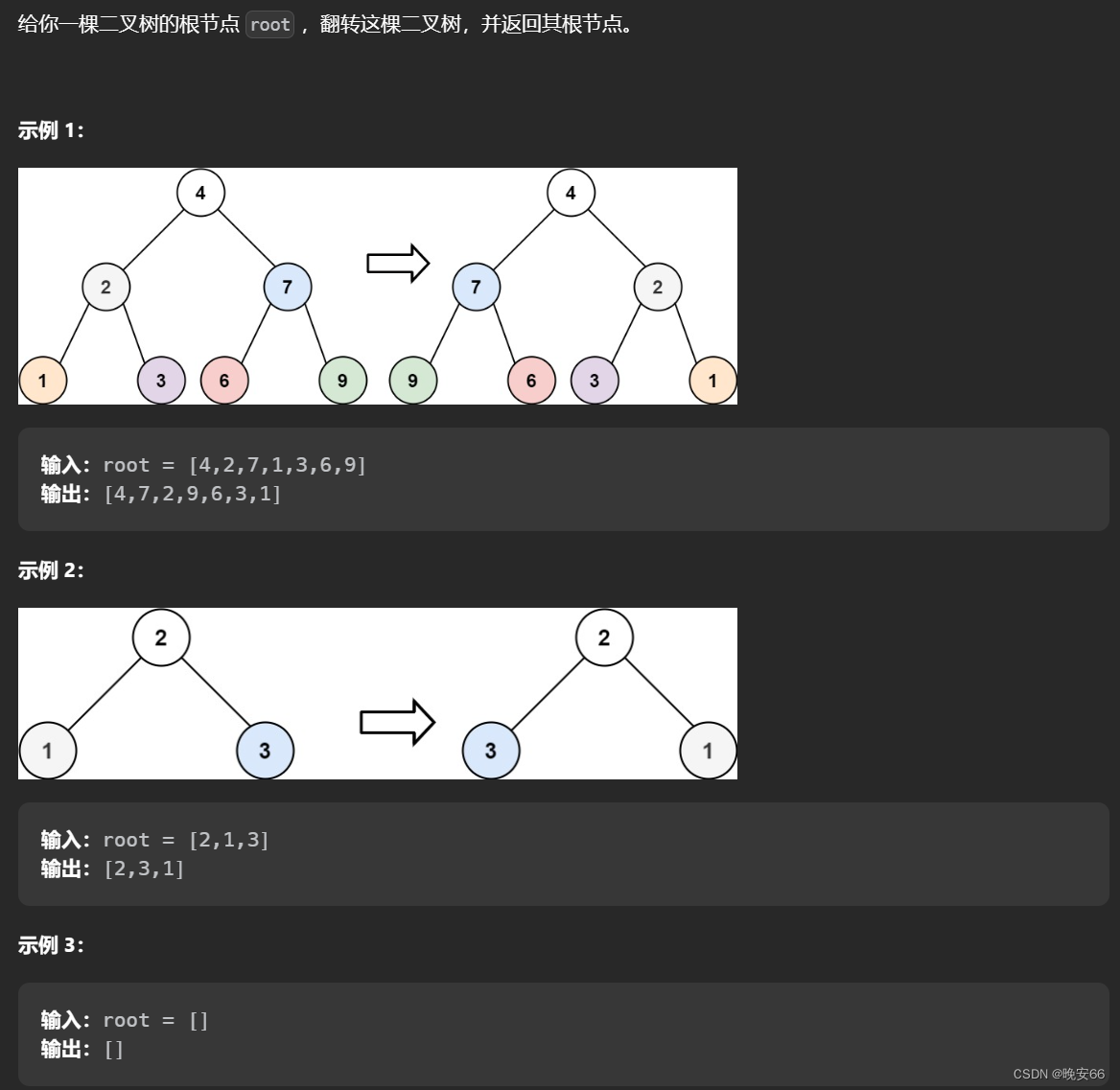
【算法与数据结构】226、LeetCode翻转二叉树
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:这道题的思路很简单,本质上就是遍历每一个节点,然后交换左右节点。我们可以用前…...
)
metaRTC6.0 new feature (一)
概要 metaRTC6.0社区版最新版是6.0.212,标准版最新版本是6.0.276,企业版基础版最新版本是6.0.362,在企业版和标准版新增了一些实用功能模块,文件数字证书模块将并入社区版。 New Feature rtsp协议支持 新增rtsp协议࿰…...
聊天机器人如何增加电子商务销售额
聊天机器人和自动化对企业和客户来说都是福音。自动对话和聊天机器人(以下统称为“自动化”)通过自动回答问题或分配会话信息来帮助用户浏览品牌网站或电商商店。即时答案对客户来说非常有用,使用自动化也可以让原本与客户聊天的客服员工专注…...

stm32 IIC通信
文章目录 IIC 通信一、硬件电路二、IIC时序基本单元三、IIC时序1.指定地址写2.当前地址读3.指定地址读 IIC 通信 IIC总线是一种通用数据总线,有两根通信线(SCL(串行时钟总线),SDA(串行数据总线))。 特点:同…...
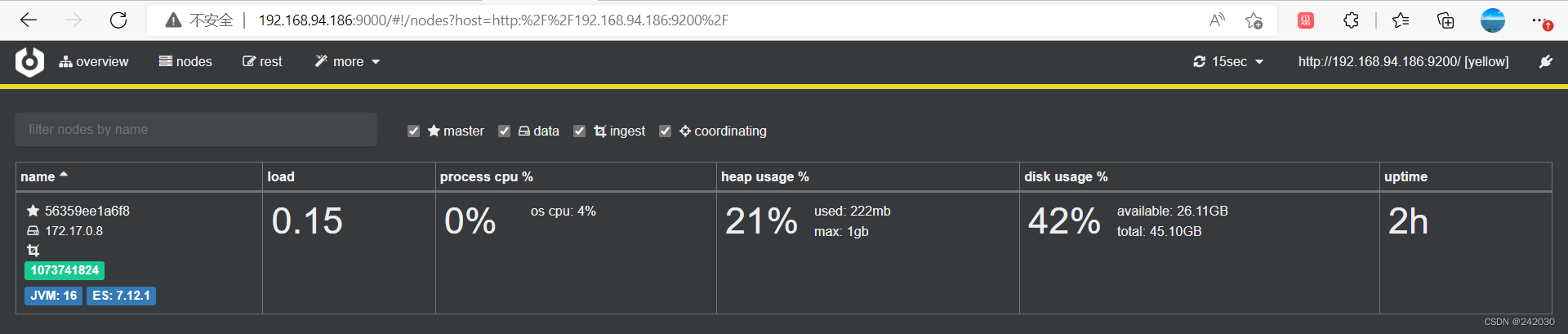
Elasticsearch监控工具Cerebro安装
Elasticsearch监控工具Cerebro安装 1、在windwos下的安装 1.1 下载安装包 https://github.com/lmenezes/cerebro/releases/download/v0.9.4/cerebro-0.9.4.zip 1.2 解压 1.3 修改配置文件 如果需要修改相关信息,编辑C:\zsxsoftware\cerebro-0.9.4\conf\applica…...

RTOS 低功耗设计原理及实现
RTOS 低功耗设计原理及实现 文章目录 RTOS 低功耗设计原理及实现👨🏫前言👨🔬Tickless Idle Mode 的原理及实现👨🚀Tickless Idle Mode 的软件设计原理👨💻Tickless Idle Mo…...
PaddleOCR C++编译出错解决方案
文章目录 前言一、环境准备1、主要环境2、源码下载3、C推理库下载 二、报错信息1.静态库调用错误2.ld returned 1 exit status 总结 前言 最近,想尝试下PaddleOCR的C推理,但是过程不如人所愿,除了很多问题,这里捡重点的说下吧&…...

89、简述RabbitMQ的架构设计
简述RabbitMQ的架构设计 BrokerQueueExchangeRoutingKeyBinding信道架构设计图Broker RabbitMQ的服务节点 Queue 队列,是RabbitMQ的内部对象,用于存储消息。RabbitMQ中消息只能存储在队列中。生产者投递消息到队列,消费者从队列中获取消息并消费。多个消费者可以订阅同一…...

63 | 图像处理
文章目录 Python图像处理什么是图像处理?Python图像处理库安装Pillow库加载和显示图像调整图像大小裁剪图像调整图像亮度、对比度和色彩平衡应用滤镜练习题Python图像处理 什么是图像处理? 图像处理是指使用计算机算法来改变图像的外观或特征。它可以用于许多不同的应用程序…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
