使用克拉默法则进行三点定圆(二维)
目录
- 1.二维圆
- 2.python代码
- 3.计算结果

本文由CSDN点云侠原创,爬虫网站请自重。
1.二维圆
已知不共线的三个点,设其坐标为 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)、 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)、 ( x 3 , y 3 ) (x_3,y_3) (x3,y3),圆的一般方程为:
A ( x 2 + y 2 ) + B x + C y + D = 0 (1) A(x^2+y^2)+Bx+Cy+D=0\tag{1} A(x2+y2)+Bx+Cy+D=0(1)
将式(1)变形可得圆的标准方程为:
( x + B 2 A ) 2 + ( y + C 2 A ) 2 = B 2 + C 2 − 4 A D 4 A 2 (2) (x+\frac{B}{2A})^2+(y+\frac{C}{2A})^2=\frac{B^2+C^2-4AD}{4A^2}\tag{2} (x+2AB)2+(y+2AC)2=4A2B2+C2−4AD(2)
将三个已知点代入式(1),可得关于 A , B , C , D A,B,C,D A,B,C,D的齐次线性方程组:
[ x 2 + y 2 x y 1 x 1 2 + y 1 2 x 1 y 1 1 x 2 2 + y 2 2 x 2 y 2 1 x 3 2 + y 3 2 x 3 y 3 1 ] ⋅ [ A B C D ] = [ 0 0 0 0 ] (3) \left[ \begin{matrix} x^2+y^2 & x & y&1\\ x_1^2+y_1^2 & x_1 & y_1&1 \\ x_2^2+y_2^2 & x_2 & y_2&1 \\ x_3^2+y_3^2 & x_3 & y_3&1 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} A\\ B \\ C \\ D \\ \end{matrix} \right]= \left[ \begin{matrix} 0\\ 0 \\ 0 \\ 0 \\ \end{matrix} \right]\tag{3} x2+y2x12+y12x22+y22x32+y32xx1x2x3yy1y2y31111 ⋅ ABCD = 0000 (3)
在三点不共线的前提下,该齐次线性方程组有非零解,其等价于系数矩阵不满秩,即有:
∣ x 2 + y 2 x y 1 x 1 2 + y 1 2 x 1 y 1 1 x 2 2 + y 2 2 x 2 y 2 1 x 3 2 + y 3 2 x 3 y 3 1 ∣ = 0 (4) \left| \begin{matrix} x^2+y^2 & x & y&1\\ x_1^2+y_1^2 & x_1 & y_1&1 \\ x_2^2+y_2^2 & x_2 & y_2&1 \\ x_3^2+y_3^2 & x_3 & y_3&1 \\ \end{matrix} \right|=0\tag{4} x2+y2x12+y12x22+y22x32+y32xx1x2x3yy1y2y31111 =0(4)
将式(4)展开,并与式(1)对比可得四个系数:
A = + ∣ x 1 y 1 1 x 2 y 2 1 x 3 y 3 1 ∣ (5) A=+\left| \begin{matrix} x_1 & y_1&1 \\ x_2 & y_2&1 \\ x_3 & y_3&1 \\ \end{matrix} \right|\tag{5} A=+ x1x2x3y1y2y3111 (5)
B = − ∣ x 1 2 + y 1 2 y 1 1 x 2 2 + y 2 2 y 2 1 x 3 2 + y 3 2 y 3 1 ∣ (6) B=-\left| \begin{matrix} x_1^2+y_1^2& y_1&1 \\ x_2^2+y_2^2 & y_2&1 \\ x_3^2+y_3^2 & y_3&1 \\ \end{matrix} \right|\tag{6} B=− x12+y12x22+y22x32+y32y1y2y3111 (6)
C = + ∣ x 1 2 + y 1 2 x 1 1 x 2 2 + y 2 2 x 2 1 x 3 2 + y 3 2 x 3 1 ∣ (7) C=+\left| \begin{matrix} x_1^2+y_1^2 & x_1 &1 \\ x_2^2+y_2^2 & x_2 &1 \\ x_3^2+y_3^2 & x_3 &1 \\ \end{matrix} \right|\tag{7} C=+ x12+y12x22+y22x32+y32x1x2x3111 (7)
D = − ∣ x 1 2 + y 1 2 x 1 y 1 x 2 2 + y 2 2 x 2 y 2 x 3 2 + y 3 2 x 3 y 3 ∣ (8) D=-\left| \begin{matrix} x_1^2+y_1^2 & x_1 & y_1 \\ x_2^2+y_2^2 & x_2 & y_2 \\ x_3^2+y_3^2 & x_3 & y_3 \\ \end{matrix} \right|\tag{8} D=− x12+y12x22+y22x32+y32x1x2x3y1y2y3 (8)
由式(2)可得圆心坐标 ( x c , y c ) (x_c,y_c) (xc,yc)和半径 r r r,即
{ x c = − B 2 A y c = − C 2 A r = B 2 + C 2 − 4 A D 4 A 2 (9) \begin{cases} x_c=-\frac{B}{2A}\\ y_c=-\frac{C}{2A}\\ r=\sqrt\frac{B^2+C^2-4AD}{4A^2} \end{cases} \tag{9} ⎩ ⎨ ⎧xc=−2AByc=−2ACr=4A2B2+C2−4AD(9)
2.python代码
import numpy as npdef three_points_fit_circle(points):P1 = points[0]P2 = points[1]P3 = points[2]# 共线检查temp01 = P1 - P2temp02 = P3 - P2temp03 = np.cross(temp01, temp02)temp = (temp03 @ temp03) / (temp01 @ temp01) / (temp02 @ temp02)if temp < 10 ** -6:print('\t三点共线, 无法确定圆')return NoneA = np.ones((3, 3))A[0, 0] = P1[0]A[0, 1] = P1[1]A[1, 0] = P2[0]A[1, 1] = P2[1]A[2, 0] = P3[0]A[2, 1] = P3[1]B = np.ones((3, 3))B[0, 0] = P1[0] ** 2 + P1[1] ** 2B[0, 1] = P1[1]B[1, 0] = P2[0] ** 2 + P2[1] ** 2B[1, 1] = P2[1]B[2, 0] = P2[0] ** 2 + P2[1] ** 2B[2, 1] = P3[1]C = np.ones((3, 3))C[0, 0] = P1[0] ** 2 + P1[1] ** 2C[0, 1] = P1[0]C[1, 0] = P2[0] ** 2 + P2[1] ** 2C[1, 1] = P2[0]C[2, 0] = P2[0] ** 2 + P2[1] ** 2C[2, 1] = P3[0]D = np.ones((3, 3))D[0, 0] = P1[0] ** 2 + P1[1] ** 2D[0, 1] = P1[0]D[0, 2] = P1[1]D[1, 0] = P2[0] ** 2 + P2[1] ** 2D[1, 1] = P2[0]D[1, 2] = P2[1]D[2, 0] = P2[0] ** 2 + P2[1] ** 2D[2, 1] = P3[0]D[2, 2] = P3[1]A = +np.linalg.det(A)B = -np.linalg.det(B)C = +np.linalg.det(C)D = -np.linalg.det(D)Xc = -B / (2 * A)Yc = -C / (2 * A)r = np.sqrt((B * B + C * C - 4 * A * D) / (4 * A * A))return Xc, Yc, r
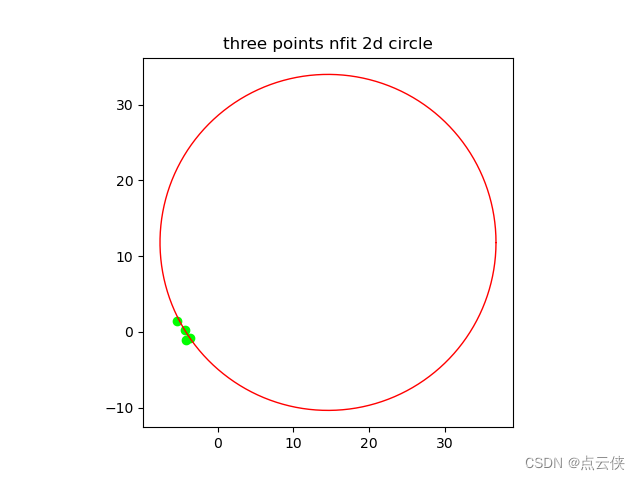
3.计算结果
圆心x坐标:14.558850728542366
圆心y坐标:11.80858513779518
圆半径:22.163390629231692
相关文章:

使用克拉默法则进行三点定圆(二维)
目录 1.二维圆2.python代码3.计算结果 本文由CSDN点云侠原创,爬虫网站请自重。 1.二维圆 已知不共线的三个点,设其坐标为 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)、 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)、 ( x 3 , y 3 ) (x_3,y_3) (x3,y3)…...
【Java】Java多线程编程基础
文章目录 1. 进程与线程1.1 进程与线程的基本认识1.1.1 进程(Process)1.1.2 线程(Thread) 1.2 为什么会有线程1.2.1 以看视频为例 2. 多线程实现2.1 Thread类实现多线程2.2 Runnable接口实现多线程2.3 Callable接口实现多线程2.3 …...

FFmpeg-4.2.4的去logo源码分析
1.源码 libavfilter/vf_delogo.c 2.源码分析 /** 去logo算法, 函数的参数解释如下: w: 输入图像的宽度 h: 输入图像的高度 logo_x: 标志区域左上角的x坐标 logo_y: 标志区域左上角的y坐标 logo_w: 标志的宽度 logo_h: 标志的高度 band: 处理区域周围的带宽大小 show: 是否在…...

深度学习(一)
目录 一、特征工程的作用 二、深度学习的应用 三、得分函数 四、损失函数 五、前向传播 六、反向传播 一、特征工程的作用 数据特征决定了模型的上限预处理和特征提取是最核心的算法与参数选择决定了如何逼近这个上限 二、深度学习的应用 无人驾驶人脸识别分辨率重构 深…...

Stream API将对象中的某一字段取出转换为list或数组
List<DevicePartMaintain> devicePartMaintainList devicePartMaintainMapper.selectDevicePartMaintainByMitId(mitId);所有id转换为List 要使用Stream流获取devicePartMaintainList中所有的id,您可以使用stream()方法将列表转换为流,然后使用…...

什么是Java中的JVM(Java虚拟机)?
JVM(Java虚拟机)是Java平台的核心组件之一,是一个用于执行Java字节码的虚拟计算机。Java源代码经过编译器编译,生成字节码文件(.class文件),然后由JVM来解释和执行这些字节码。JVM负责将字节码翻…...
springboot + redis + 注解 + 拦截器 实现接口幂等性校验
一、概念 幂等是一个数学与计算机学概念,在数学中某一元运算为幂等时,其作用在任一元素两次后会和其作用一次的结果相同。在计算机中编程中,一个幂等操作的特点是其任意多次执行所产生的影响均与一次执行的影响相同。 幂等函数或幂等方法是…...
PLC编程:关键在于模拟操作流程和实现控制
PLC编程的核心是通过程序描述流程,完成控制过程。因此,掌握PLC编程语言和基本功能实现是必要的。 PLC语言主要分为梯形图、语句和功能图。梯形图适合基本逻辑描述,语句表用于数据处理,相对较难理解。步进式功能图的状态函数描述很…...
List的各种排序
目录 Collections.sort对list进行排序 对象中某个属性进行排序 通过比较器进行比较 JAVA8特性Stream流进行排序 Stream升降序组合使用 Collections.sort对list进行排序 public static void main(String[] args) {List<Integer> list new ArrayList<>();list…...
在自定义数据集上微调Alpaca和LLaMA
本文将介绍使用LoRa在本地机器上微调Alpaca和LLaMA,我们将介绍在特定数据集上对Alpaca LoRa进行微调的整个过程,本文将涵盖数据处理、模型训练和使用流行的自然语言处理库(如Transformers和hugs Face)进行评估。此外还将介绍如何使用grado应用程序部署和…...
)
Python 实现接口类的两种方式+邮件提醒+动态导入模块+反射(参考Django中间件源码)
实现抽象类的两种方式 方式一 from abc import ABCMeta from abc import abstractmethodclass BaseMessage(metaclassABCMeta):abstractmethoddef send(self,subject,body,to,name):pass 方式二 class BaseMessage(object):def send(self, subject, body, to, name):raise …...
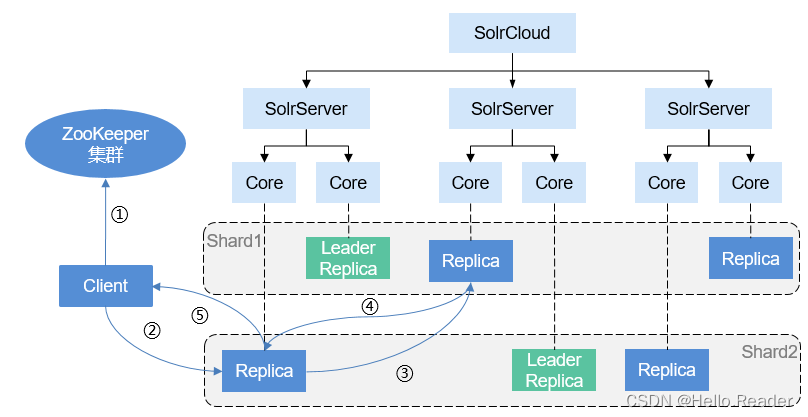
Solr原理剖析
一、简介 Solr是一个高性能、基于Lucene的全文检索服务器。Solr对Lucene进行了扩展,提供了比Lucene更为丰富的查询语言,并实现了强大的全文检索功能、高亮显示、动态集群,具有高度的可扩展性。同时从Solr 4.0版本开始,支持SolrCl…...

解决 “无法将 ‘npm‘ 项识别为 cmdlet、函数、脚本文件或可运行程序的名称“ 错误的方法
系列文章目录 文章目录 系列文章目录前言一、错误原因:二、解决方法:三、注意事项:总结 前言 在使用 npm 进行前端项目开发时,有时会遇到错误信息 “无法将 ‘npm’ 项识别为 cmdlet、函数、脚本文件或可运行程序的名称”&#x…...

Python 电商API 开发最佳实践
一、简介 当你打卡了一家北京最具有地中海特色的餐厅,当我们在餐厅点餐时,服务员会给我们一份菜单,菜单上列出了所有可供选择的菜品和饮料。我们可以在菜单上选择我们想要的食物和饮料,然后告诉服务员我们的选择。服务员会根据我…...
JAVA基础-集合(List与Map)
目录 引言 一,Collection集合 1.1,List接口 1.1.1,ArrayList 1.1.1.1,ArrayList的add()添加方法 1.1.1.2,ArrayList的remove()删除方法 1.1.1.3,ArrayList的contai…...
19 QListWidget控件
Tips: 对于列表式数据可以使用QStringList进行左移一块输入。 代码: //listWidget使用 // QListWidgetItem * item new QListWidgetItem("锄禾日当午"); // QListWidgetItem * item2 new QListWidgetItem("汗滴禾下土"); // ui->…...

手动安装docsify
安装docsify详见:docsify 1、下载 wget https://codeload.github.com/docsifyjs/docsify/zip/refs/heads/master -o docsify-master.zip 2、解压 unzip docsify-master.zip 3、移动文件到nginx的html所在目录【略】 4、配置nginx,示例如下 locati…...
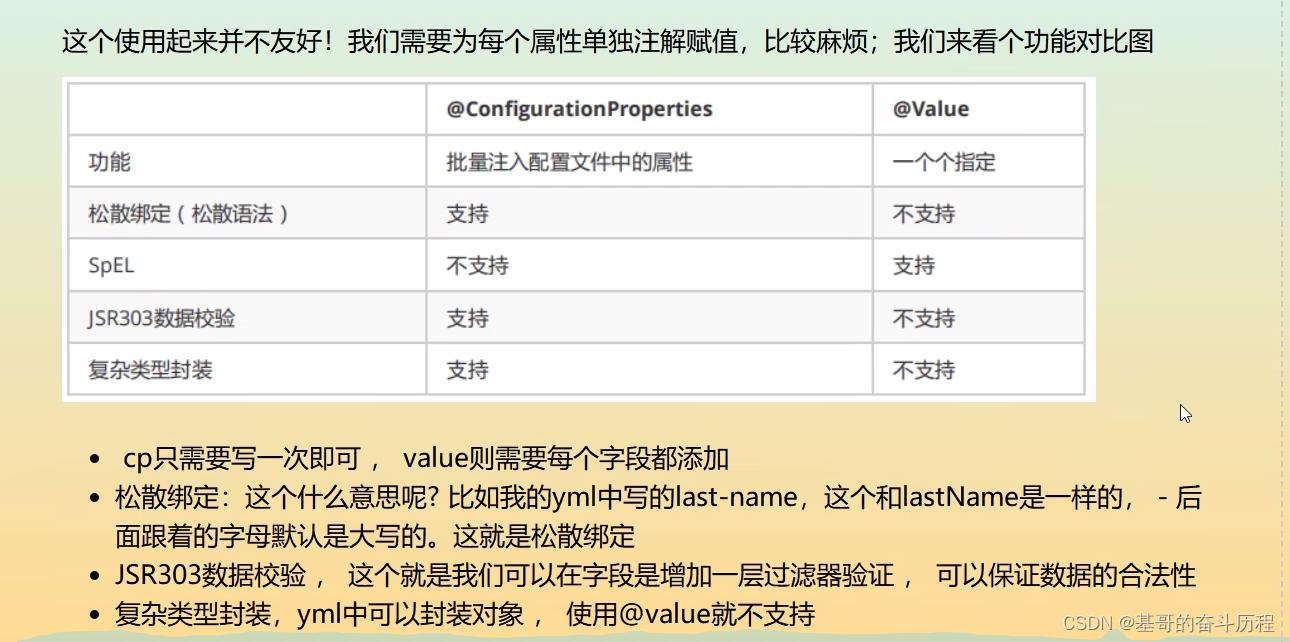
yaml语法详解
#kv #对空格的严格要求十分高 #注入到我们的配置类中 #普通的keyvalue name: qinjiang#对象 student:name: qingjiangage: 3#行内写法 student1: {name: qinjiang,age: 3}#数组 pets:- cat- dog- pigpet: [cat,dog,pig]yaml可以给实体类赋值 person:name: kuangshenage: 19happ…...

ubuntu下tmux安装
目录 0. 前言1. Tmux介绍2. 安装3. 验证安装 0. 前言 本节安装tmux终端复用工具,在Ubuntu中运行一些服务或脚本的时候往往不能退出终端,需要一直挂着。在有图形界面的linux中你还可以新开一个终端去做别的事,但是在无界面linux中,…...
ssh打开远程vscode
如果想要远程打开其他终端的vscode,首先要知道远程终端的ip地址和用户名称以及用户密码 1、打开本地vscode 2、点击左下角蓝色区域 3、页面上部出现如下图,点击ssh,我这里已经连接,所以是connect to host 4、选择Add New SSH Host…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
