【C#性能】C# 语言中的数组迭代
一、说明
可迭代性,是数组等操作的根本;在C++程序开发过程中,可迭代操作是非常普遍、非常广泛的,然而,对这种操作知道多少,又不知道多少,都将影响开发灵活性、开发的进度。因此,本文干脆系统地全部列举这种应用,以便在使用时查阅。
二、从简单示例入手
实现数组中项的总和非常简单。我认为大多数开发人员会以这种方式实现它:
static int Sum(int[] array)
{var sum = 0;for (var index = 0; index < array.Length; index++)sum += array[index];return sum;
}C# 中实际上有一个更简单的替代方法:
static int Sum(int[] array)
{var sum = 0;foreach (var item in array)sum += item;return sum;
} 另一种替代方法是使用 LINQ 提供的操作。它可以应用于任何可枚举项,包括数组。Sum()
那么,这三者在性能方面如何公平呢?

该基准测试比较了 .NET 10、1 和 000 上大小为 6 和 7.8 的阵列的性能。int
您可以看到,使用循环 比使用循环快 30% 左右 。foreachfor
在最新的 .NET 版本中,LINQ 实现有了很大的改进。它在 .NET 6 中要慢得多,但在 .NET 7 中要慢得多,对于 .NET 8 中的大型数组来说要快得多。
三、foreachfor
怎么能比循环更快?foreachfor和循环都是循环的语法糖。当在数组上使用这些代码时,编译器实际上会生成非常相似的代码。forforeachwhile
你可以在SharpLab中看到以下代码:
var array = new[] {0, 1, 2, 3, 4, 5 };Console.WriteLine(Sum_For());
Console.WriteLine(Sum_ForEach());int Sum_For()
{var sum = 0;for (var index = 0; index < array.Length; index++)sum += array[index];return sum;
}int Sum_ForEach()
{var sum = 0;foreach (var item in array)sum += item;return sum;
}编译器生成以下内容:
[CompilerGenerated]
private static int <<Main>$>g__Sum_For|0_0(ref <>c__DisplayClass0_0 P_0)
{int num = 0;int num2 = 0;while (num2 < P_0.array.Length){num += P_0.array[num2];num2++;}return num;
}[CompilerGenerated]
private static int <<Main>$>g__Sum_ForEach|0_1(ref <>c__DisplayClass0_0 P_0)
{int num = 0;int[] array = P_0.array; // copy array referenceint num2 = 0;while (num2 < array.Length){int num3 = array[num2];num += num3;num2++;}return num;
}代码非常相似,但请注意,添加了对数组的引用作为局部变量。这允许 JIT 编译器删除边界检查,从而使迭代速度更快。检查生成的程序集的差异:foreach
Program.<<Main>$>g__Sum_For|0_0(<>c__DisplayClass0_0 ByRef)L0000: sub rsp, 0x28L0004: xor eax, eaxL0006: xor edx, edxL0008: mov rcx, [rcx]L000b: cmp dword ptr [rcx+8], 0L000f: jle short L0038L0011: nop [rax]L0018: nop [rax+rax]L0020: mov r8, rcxL0023: cmp edx, [r8+8]L0027: jae short L003dL0029: mov r9d, edxL002c: add eax, [r8+r9*4+0x10]L0031: inc edxL0033: cmp [rcx+8], edxL0036: jg short L0020L0038: add rsp, 0x28L003c: retL003d: call 0x000002e975d100fcL0042: int3Program.<<Main>$>g__Sum_ForEach|0_1(<>c__DisplayClass0_0 ByRef)L0000: xor eax, eaxL0002: mov rdx, [rcx]L0005: xor ecx, ecxL0007: mov r8d, [rdx+8]L000b: test r8d, r8dL000e: jle short L001fL0010: mov r9d, ecxL0013: add eax, [rdx+r9*4+0x10]L0018: inc ecxL001a: cmp r8d, ecxL001d: jg short L0010L001f: ret这导致基准测试中的性能得到改善。
请注意,在 SharpLab 中,数组已经是一个局部变量,不会生成副本。在这种情况下,性能是等效的。
四、对数组进行切片
有时我们可能只想迭代数组的一部分。再一次,我认为大多数开发人员会实现以下内容:
static int Sum(int[] source, int start, int length)
{var sum = 0;for (var index = start; index < start + length; index++)sum += source[index];return sum;
}这可以通过使用 Span.Slice() 方法轻松转换为 foreach:
static int Sum(int[] source, int start, int length) => Sum(source.AsSpan().Slice(start, length));static int Sum(ReadOnlySpan<int> source)
{var sum = 0;foreach (var item in source)sum += item;return sum;
}那么,这些展会在表现方面如何呢?
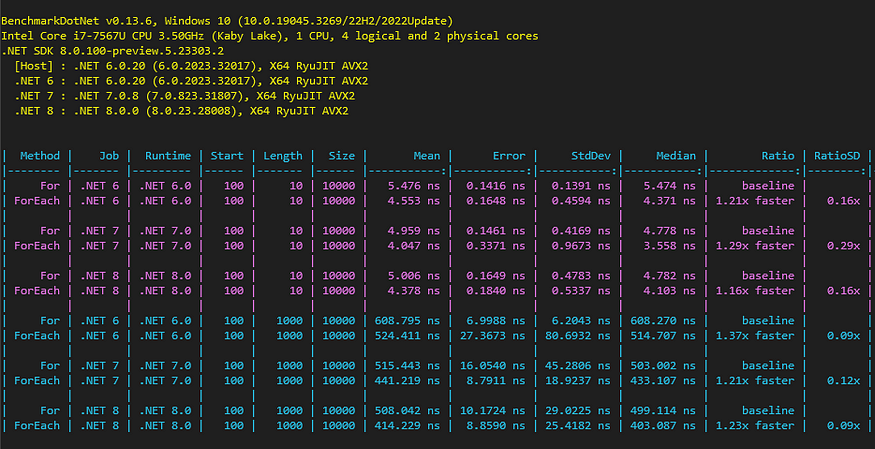
在数组的一部分上使用也比使用循环好 20% 左右。foreachfor
五、LINQ
检查 in 的源代码,对于 .NET 8 之前的 .NET 版本,您会发现它使用循环 。那么,如果使用 a 比 a 快,为什么在这种情况下它这么慢?Sum()System.Linqforeachforeachfor
此实现是 类型的扩展方法。与 和 操作不同,当源在数组中时没有特殊情况。编译器将此实现转换为如下所示的内容:Sum()IEnumerable<int>Count()Where()Sum()
static int Sum(this IEnumerable<int> source)
{var sum = 0;IEnumerator<int> enumerator = source.GetEnumerator();try{while(enumerator.MoveNext())sum += enumerator.Current;}finally{enumerator?.Dispose()}return sum;
}此代码存在多个性能问题:
GetEnumerator()返回。这意味着枚举器是引用类型,这意味着它必须在堆上分配,从而增加垃圾回收器的压力。IEnumerator<T>IEnumerator<T>来自。然后,它需要 来释放枚举器,因此无法内联此方法。IDisposabletry/finally- 对 的迭代需要调用方法和属性。由于枚举器是引用类型,因此这些调用是虚拟的。
IEnumerable<T>MoveNext()Current
所有这些都使数组的枚举速度慢得多。
注意:请查看我的另一篇文章“值类型枚举器的性能与引用类型枚举器的性能”,以了解这两种类型的枚举器之间的性能差异。
.NET 8 的性能要好得多,因为它会在 源是数组或 .如果是 or 的数组或列表,它会通过使用 SIMD 进行更多优化,从而允许同时对多个项目求和。Sum()List<T>intlong
注意:请查看我的另一篇文章“.NET 中的单指令多数据 (SIMD)”,了解 SIMD 的工作原理以及如何在代码中使用。
六、结论
数组的迭代是编译器可以执行代码优化的特例。的使用保证了这些优化的最佳条件。foreach
将数组转换为 会使其迭代速度慢得多。IEnumerable<T>
并非所有 LINQ 方法都针对数组的情况进行了优化。在 .NET 8 之前,最好使用 Sum() 方法的自定义实现。
相关文章:

【C#性能】C# 语言中的数组迭代
一、说明 可迭代性,是数组等操作的根本;在C程序开发过程中,可迭代操作是非常普遍、非常广泛的,然而,对这种操作知道多少,又不知道多少,都将影响开发灵活性、开发的进度。因此,本文干…...
全志F1C200S嵌入式驱动开发(解决spi加载过慢的问题)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing @163.com】 之前的几个章节当中,我们陆续解决了spi-nor驱动的问题、uboot支持spi-nor的问题。按道理来说,下面要做的应该就是用uboot的loady命令把kernel、dtb、rootfs这些文件下载到ddr,然…...
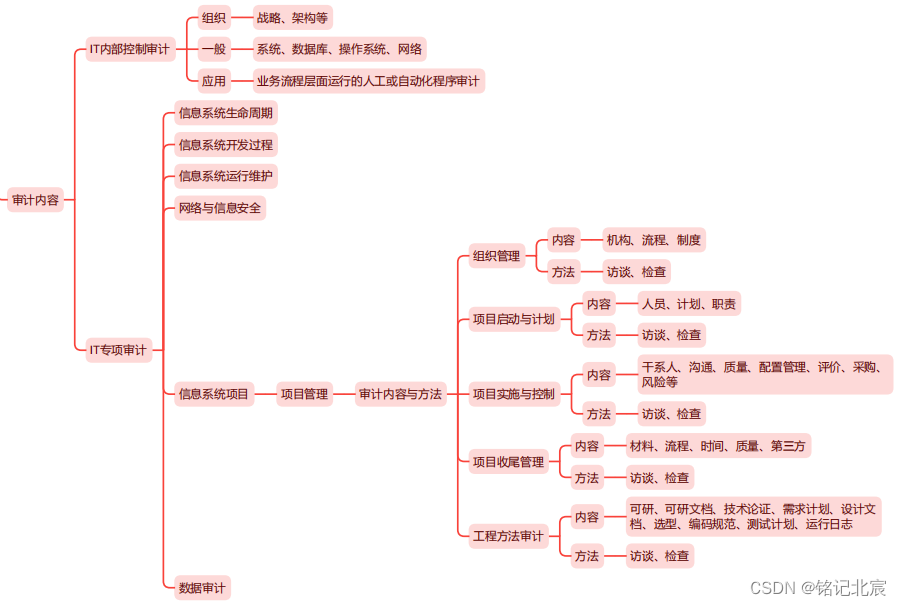
信息系统项目管理师(第四版)教材精读思维导图-第三章信息系统治理
请参阅我的另一篇文章,综合介绍软考高项: 信息系统项目管理师(软考高项)备考总结_计算机技术与软件专业技术_铭记北宸的博客-CSDN博客 目录 3.1 IT治理 3.2 IT审计 3.1 IT治理 3.2 IT审计...

区间预测 | MATLAB实现基于QRF随机森林分位数回归多变量时间序列区间预测模型
区间预测 | MATLAB实现基于QRF随机森林分位数回归多变量时间序列区间预测模型 目录 区间预测 | MATLAB实现基于QRF随机森林分位数回归多变量时间序列区间预测模型效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab实现基于QRF随机森林分位数回归多变量时间序列区间…...
五步快速搭建个性化外卖小程序商城
随着人们生活节奏的加快,外卖行业蓬勃发展。为了满足用户的需求,许多企业开始使用小程序商城来提供外卖服务。那么,如何制作一个功能完善、用户友好的外卖小程序商城呢?下面就来为大家详细介绍一下制作的步骤。 首先,我…...

jenkins中配置了发送邮件,构建后却没有发邮件Not sent to the following valid addresse
【问题描述】:jekins中配置了发送邮件,构建后却没有发邮件的问题,构建报错:Not sent to the following valid addresse 【报错显示】: 【问题定位】:Extended E-mail Notification中,没有配置…...

装箱问题(背包问题)
题目描述 有一个箱子容量为v(正整数,o≤v≤20000),同时有n个物品(o≤n≤30),每个物品有一个体积 (正整数)。要求从 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。 输入格式 第一行,一个整…...

【C++】总结4-this指针
文章目录 什么是this指针this指针存在的意义this指针的特性this指针存在哪里this指针可以为空吗 什么是this指针 C编译器给每个非静态成员函数增加了一个隐藏的指针参数,让该指针指向当前对象(函数运行时调用该函数的对象),在函数…...

go压力测试
压力测试 1.1.1. Go怎么写测试用例 开发程序其中很重要的一点是测试,我们如何保证代码的质量,如何保证每个函数是可运行,运行结果是正确的,又如何保证写出来的代码性能是好的,我们知道单元测试的重点在于发现程序设计…...
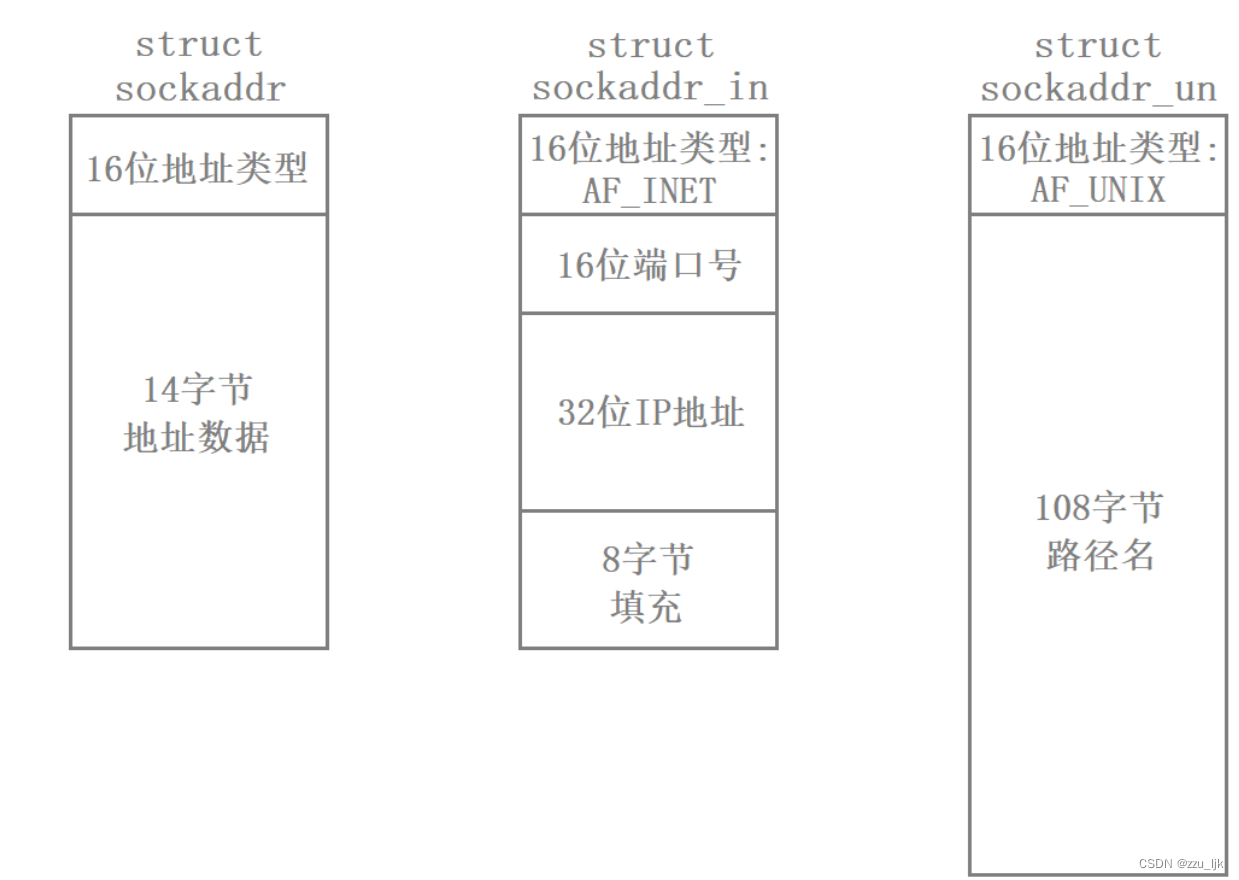
【计算机网络】socket编程基础
文章目录 1. 源IP地址和目的IP地址2. 理解MAC地址和目的MAC地址3. 理解源端口号和目的端口号4. PORT与PID5. 认识TCP协议和UDP协议6. 网络字节序7. socket编程接口7.1 socket常见API7.2 sockaddr结构 1. 源IP地址和目的IP地址 因特网上的每台计算机都有一个唯一的IP地址&#…...
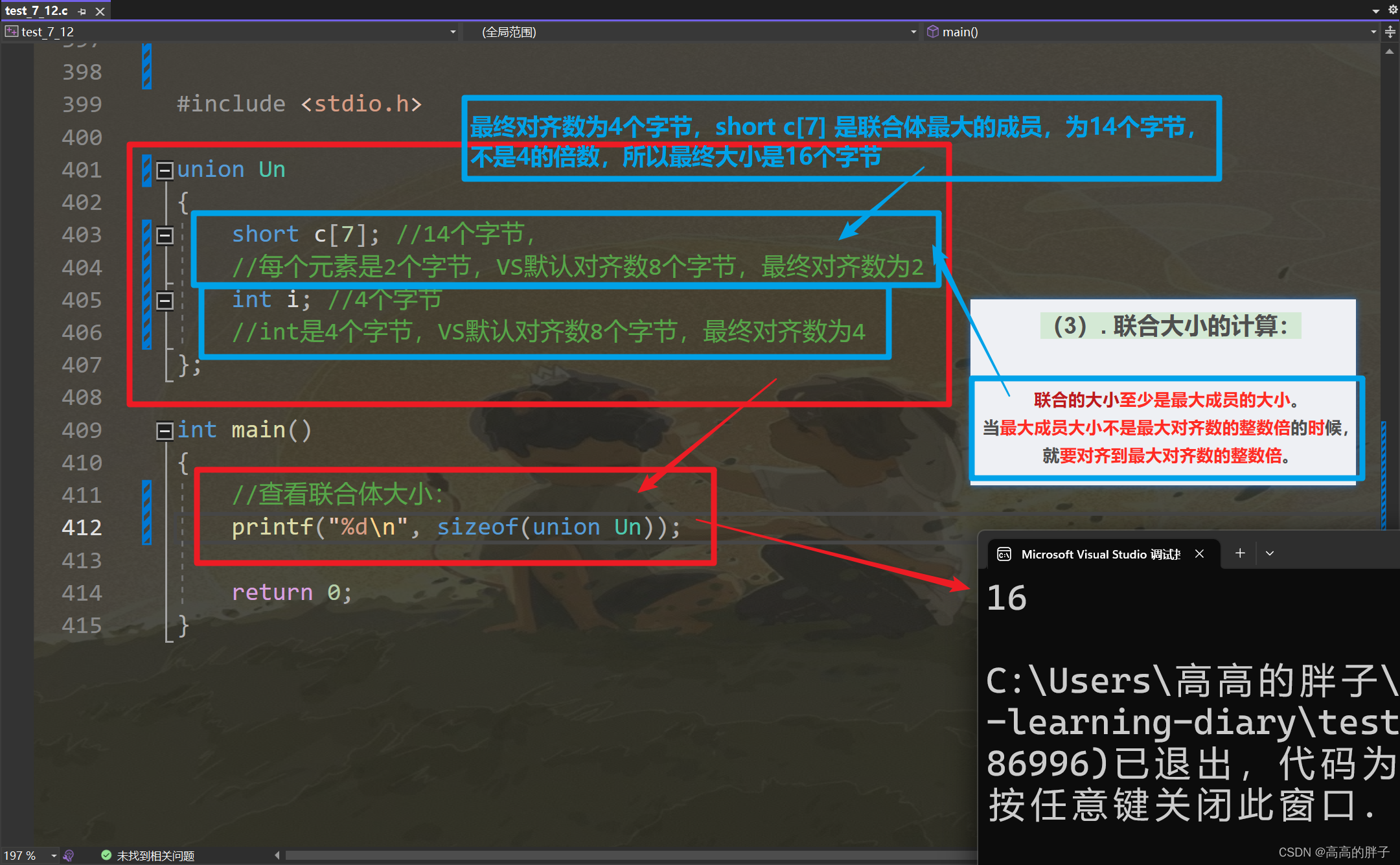
学C的第三十天【自定义类型:结构体、枚举、联合】
相关代码gitee自取:C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第二十九天【字符串函数和内存函数的介绍(二)】_高高的胖子的博客-CSDN博客 1 . 结构体 (1). 结构体的基础知识: 结构…...
:通过noVNC实现网页访问vnc)
Ubuntu(20.04):通过noVNC实现网页访问vnc
VNC vnc是日常工作和生产环境中常用的远程桌面控制工具。 通常需要在被访问的系统中安装vncserver。 然后在发起访问端,安装客户端软件,比如VNC Viewer。 noVNC noVNC提供了一种方案,就是通过web浏览器直接访问vnc server。 其实现的基本原理是: 1.已经安装好的vncse…...

OpenAI的Function calling 和 LangChain的Search Agent
OpenAI的Function calling openai最近发布的gpt-3.5-turbo-0613 和 gpt-4-0613版本模型增加了function calling的功能,该功能通过定义功能函数,gpt通过分析问题和函数功能描述来决定是否调用函数,并且生成函数对应的入参。函数调用的功能可以…...

【mysql数据库】MySQL7在Centos7的环境安装
说明: 安装与卸载中,用户全部切换成为root,⼀旦安装,普通用户就能使用。初期练习,mysql不进行用户管理,全部使⽤root进⾏,尽快适应mysql语句,后⾯学了用户管理,在考虑新…...

基于vue+element 分页的封装
目录标题 项目场景:认识分页1.current-page2.page-sizes3.page-size4.layout5.total6.size-change7.current-change 封装分页:创建paging:进行封装 页面中使用:引入效果 项目场景: 分页也是我们在实际应用当中非常常见…...

面试题模拟
C# 装箱和拆箱是什么? 装箱是指用堆空间来存放值类型数据 拆箱是指将存放在堆空间的值类型数据转换到栈空间 值和引用类型在变量赋值时的区别是什么? 值类型的数据赋值的时候是指向同一块内存区域,当前一个改变的时候后一个也会跟着改变。 引…...
Linux6.13 Docker LNMP项目搭建
文章目录 计算机系统5G云计算第四章 LINUX Docker LNMP项目搭建一、项目环境1.环境描述2.容器ip地址规划3.任务需求 二、部署过程1.部署构建 nginx 镜像2.部署构建 mysql 镜像3.部署构建 php 镜像4.验证测试 计算机系统 5G云计算 第四章 LINUX Docker LNMP项目搭建 一、项目…...

数据包协议栈处理
看了两个不错的帖子,记录一下。 4.2 TCP Segmentation Offload(TSO)_Remy的学习记录-CSDN博客_tcp-segmentation-offload Linux内核参数之rp_filter - 萝卜1992 - 博客园...

html刷新图片
文章目录 前言网页整体刷新改变图像的url 备注 前言 海思3516的一个开发板,不断的采集图像编码为jpeg,保存为同一个文件。打算用网页实现查看视频的效果,需要前端能够自动刷新。 目前找到了两个方法,一个是网页的不断刷新&#…...

PHP反序列化漏洞之魔术方法
一、魔术方法 PHP魔术方法(Magic Methods)是一组特殊的方法,它们在特定的情况下会被自动调用,用于实现对象的特殊行为或提供额外功能。这些方法的名称都以双下划线开头和结尾,例如: __construct()、__toString()等。 …...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
