装箱问题(背包问题)
题目描述
有一个箱子容量为v(正整数,o≤v≤20000),同时有n个物品(o≤n≤30),每个物品有一个体积 (正整数)。要求从 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。
输入格式
第一行,一个整数,表示箱子容量; 第二行,一个整数,表示有n个物品; 接下来n行,分别表示这n个物品的各自体积。
输出格式
一个整数,表示箱子剩余空间。
样例输入
24 6 8 3 12 7 9 7
样例输出
0
解题思路
这一题乍一看与背包问题相似,但是相较于背包问题更加简单,没有价值设定,一开始我试着用更加通俗易懂的方法写,即从大到小依次遍历,进行装箱,直到装不下为止
我用了两个for循环以求left(剩余空间大小),即
//第一个for循环遍历到 装入下一个箱子,空间为负为止
for(int i=0;i<n;i++)//将箱子从大到小依次装到箱中{if(arr[i]+sum<v){sum+=arr[i];}}left=v-sum;//这里空间剩余:3
for(int i=0;i<n;i++)
{if(arr[i]<=left)//以剩余空间作为判断条件 { sum+=arr[i];left=v-sum;//更新left}
}最终代码得
#include<stdio.h>int main()
{int v, n;//v表示体积,n表示物品个数int max, temp,sum=0,left;scanf("%d", &v);scanf("%d", &n);int arr[n];for (int i = 0; i < n; i++){scanf("%d", &arr[i]);}for (int i = 0; i < n; i++)//冒泡排序,将体积从大到小放入arr[i]中{for(int j=0;j < n-1-i;j++){if (arr[j + 1] > arr[j]){temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
/*for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
*/for(int i=0;i<n;i++)//将箱子从大到小依次装到箱中{if(arr[i]+sum<v){sum+=arr[i];}}left=v-sum;//这里空间剩余:3for(int i=0;i<n;i++){if(arr[i]<=left)//以剩余空间作为判断条件sum+=arr[i];left=v-sum;}printf("%d",left);return 0;
}但这样写不具有通用性,还是要用到动态规划算法,代码如下
其中最重要的一段即
for(i=1;i<=n;i++)
//从1开始是因为当v=0, 箱子装不下任何东西,i=0表示第0件物品,即没有物品,所以跳过 for(j=v;j>=1;j--)
/*
把数组压缩到一维必须逆序,因为01背包问题就是由旧值推新值,从前面开始的话,旧值就会过早被新值覆盖
例如:
如果a[30]在a[20]的基础上加了w[i]=10,表示30容量这个背包它拿了w[i]=10这个东西了,但是--它没有考虑:a[20]里面是否拿过w[i]=10这个东西,所以要j--;
也就是说箱子的体积从小到大遍历,物品从大到小开始装,这样才能避免重复装入物品
*/{//j可以看作箱子当前的容量 if(w[i]<=j)//判断是否能装下物品i a[j]=MAX(a[j],a[j-w[i]]+w[i]);//原式为a[i][j]=MAX(a[i-1][j],a[i-1][j-w[i]]+w[i]) }for(j=v;j>=1;j--)
还是不懂为什么j--
那么就多写:
for(j=v;j>=1;j--)的情况

for(j=1;j<=v;j++)的情况
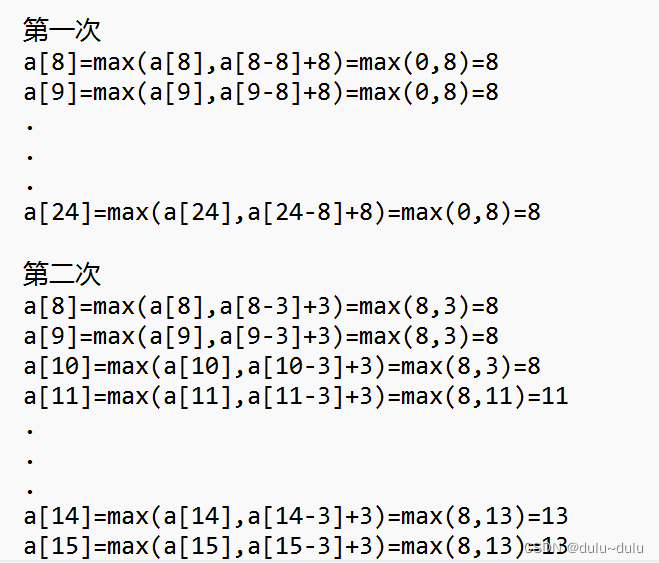
可以看到从a[14]开始,旧值已经覆盖新值了
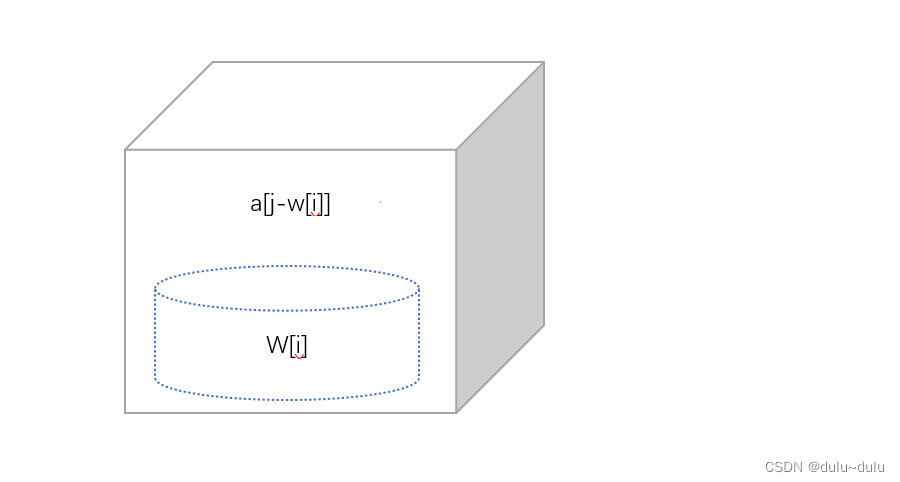
注:a[j]为没放入,a[j-w[i]]+w[i]为放入
如下图所示a[j]为V(容量),a[j-w[i]]为放入w[i]后剩余的容量,a[j-w[i]]+w[i]为放入w[i]后的容量大小,不理解的可以依据上图观察规律:
最终代码如下
#include<stdio.h>int w[40]={0};//注意初始化 ,这里表示物品的体积
int a[30011]={0};//这里表示v
int MAX(int n,int m)
{if(m<=n) return n;else return m;
}
int main()
{int n,i,j,v;scanf("%d",&v); scanf("%d",&n); for(i=1;i<=n;i++)scanf("%d",&w[i]);for(i=1;i<=n;i++)//从1开始是因为当v=0, 箱子装不下任何东西,i=0表示第0件物品,即没有物品,所以跳过 for(j=v;j>=1;j--)
/*
把数组压缩到一维必须逆序,因为01背包问题就是由旧值推新值,从前面开始的话,旧值就会过早被新值覆盖
例如:
如果a[30]在a[20]的基础上加了w[i]=10,表示30容量这个背包它拿了w[i]=10这个东西了,但是--它没有考虑:a[20]里面是否拿过w[i]=10这个东西,所以要j--;
也就是说箱子的体积从小到大遍历,物品从大到小开始装,这样才能避免重复装入物品
*/{//j可以看作箱子当前的容量 if(w[i]<=j)//判断是否能装下物品i a[j]=MAX(a[j],a[j-w[i]]+w[i]);//原式为a[i][j]=MAX(a[i-1][j],a[i-1][j-w[i]]+w[i]) }// a[j]为不拿,a[j-w[i]]+w[i]为拿//a[j-w[i]]+w[i]意为放入物品i后,总占用空间=物品i所占的空间+箱子剩余的空间 j-w[i] 所能被占用的最大空间 a[j-w[i]]printf("%d",v-a[v]);//此时的a[v]表示当容量为v时,箱子已被占用空间a[v] return 0;
}这是@佳佳佳佳佳博主的图,有助于理解
MAX(a[i-1][j],a[i-1][j-w[i]]+w[i])

这是最简单的背包问题,一定要理解,如果还有点迷糊的话,可以看看这篇文章
http://t.csdn.cn/X7GLD
或者
http://t.csdn.cn/CleVM
相关文章:

装箱问题(背包问题)
题目描述 有一个箱子容量为v(正整数,o≤v≤20000),同时有n个物品(o≤n≤30),每个物品有一个体积 (正整数)。要求从 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小。 输入格式 第一行,一个整…...

【C++】总结4-this指针
文章目录 什么是this指针this指针存在的意义this指针的特性this指针存在哪里this指针可以为空吗 什么是this指针 C编译器给每个非静态成员函数增加了一个隐藏的指针参数,让该指针指向当前对象(函数运行时调用该函数的对象),在函数…...

go压力测试
压力测试 1.1.1. Go怎么写测试用例 开发程序其中很重要的一点是测试,我们如何保证代码的质量,如何保证每个函数是可运行,运行结果是正确的,又如何保证写出来的代码性能是好的,我们知道单元测试的重点在于发现程序设计…...
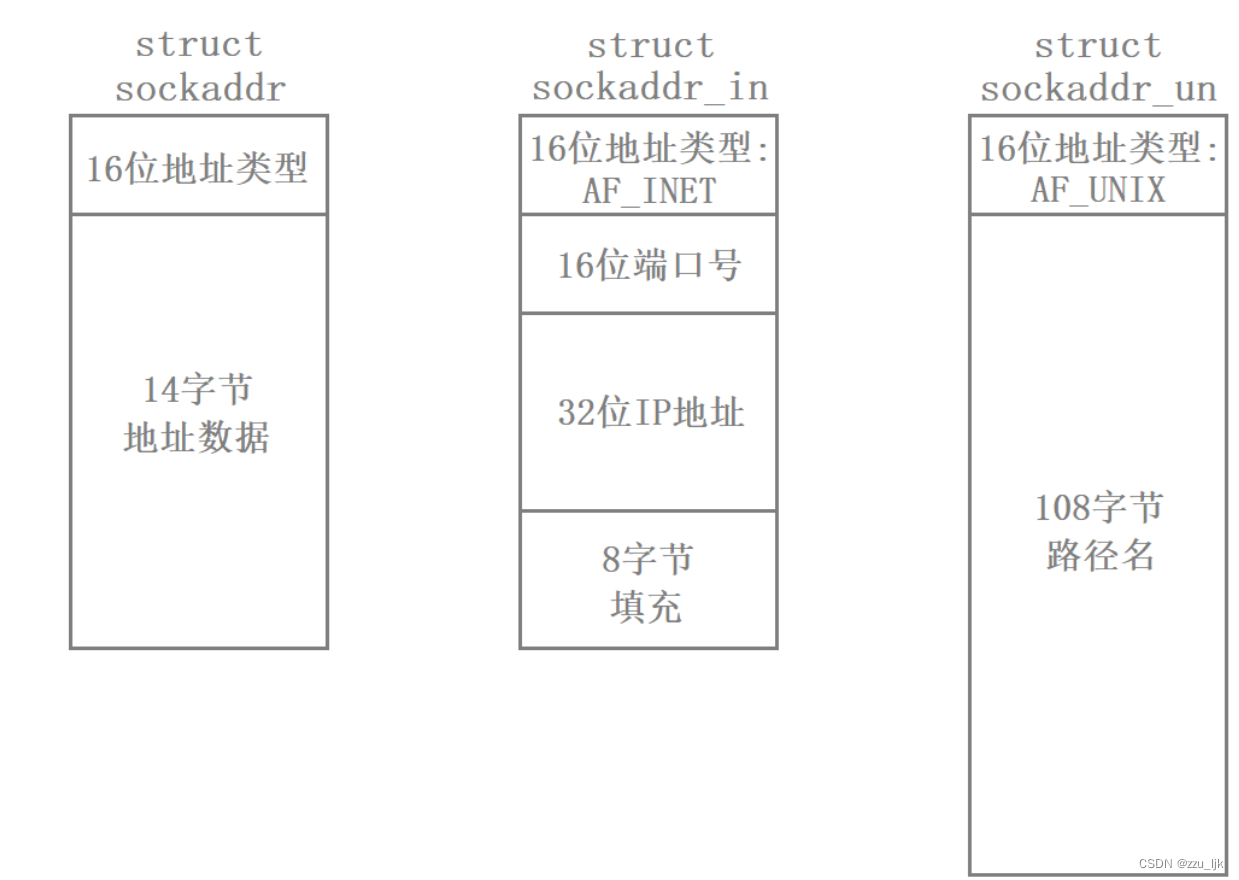
【计算机网络】socket编程基础
文章目录 1. 源IP地址和目的IP地址2. 理解MAC地址和目的MAC地址3. 理解源端口号和目的端口号4. PORT与PID5. 认识TCP协议和UDP协议6. 网络字节序7. socket编程接口7.1 socket常见API7.2 sockaddr结构 1. 源IP地址和目的IP地址 因特网上的每台计算机都有一个唯一的IP地址&#…...
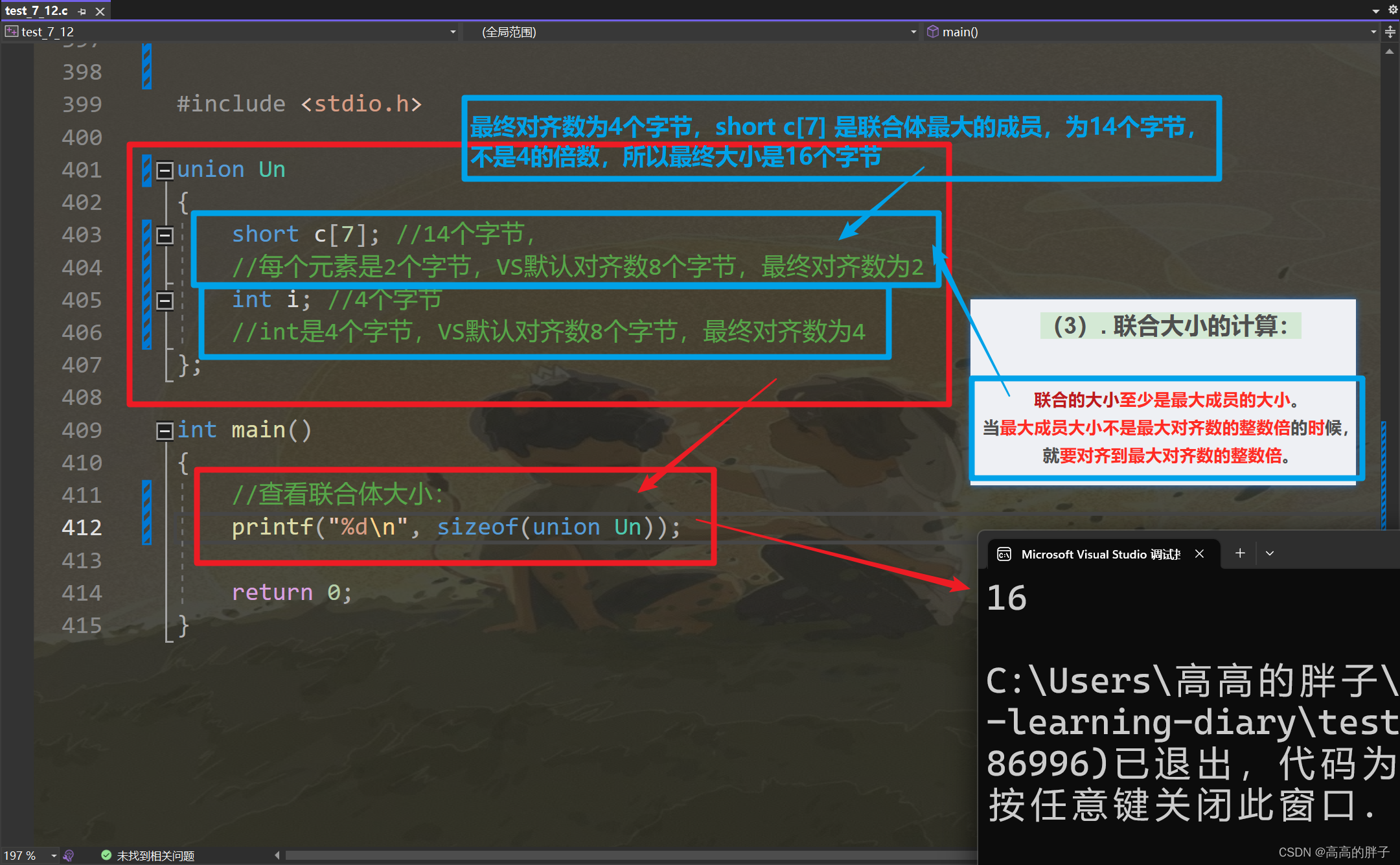
学C的第三十天【自定义类型:结构体、枚举、联合】
相关代码gitee自取:C语言学习日记: 加油努力 (gitee.com) 接上期: 学C的第二十九天【字符串函数和内存函数的介绍(二)】_高高的胖子的博客-CSDN博客 1 . 结构体 (1). 结构体的基础知识: 结构…...
:通过noVNC实现网页访问vnc)
Ubuntu(20.04):通过noVNC实现网页访问vnc
VNC vnc是日常工作和生产环境中常用的远程桌面控制工具。 通常需要在被访问的系统中安装vncserver。 然后在发起访问端,安装客户端软件,比如VNC Viewer。 noVNC noVNC提供了一种方案,就是通过web浏览器直接访问vnc server。 其实现的基本原理是: 1.已经安装好的vncse…...

OpenAI的Function calling 和 LangChain的Search Agent
OpenAI的Function calling openai最近发布的gpt-3.5-turbo-0613 和 gpt-4-0613版本模型增加了function calling的功能,该功能通过定义功能函数,gpt通过分析问题和函数功能描述来决定是否调用函数,并且生成函数对应的入参。函数调用的功能可以…...

【mysql数据库】MySQL7在Centos7的环境安装
说明: 安装与卸载中,用户全部切换成为root,⼀旦安装,普通用户就能使用。初期练习,mysql不进行用户管理,全部使⽤root进⾏,尽快适应mysql语句,后⾯学了用户管理,在考虑新…...

基于vue+element 分页的封装
目录标题 项目场景:认识分页1.current-page2.page-sizes3.page-size4.layout5.total6.size-change7.current-change 封装分页:创建paging:进行封装 页面中使用:引入效果 项目场景: 分页也是我们在实际应用当中非常常见…...

面试题模拟
C# 装箱和拆箱是什么? 装箱是指用堆空间来存放值类型数据 拆箱是指将存放在堆空间的值类型数据转换到栈空间 值和引用类型在变量赋值时的区别是什么? 值类型的数据赋值的时候是指向同一块内存区域,当前一个改变的时候后一个也会跟着改变。 引…...
Linux6.13 Docker LNMP项目搭建
文章目录 计算机系统5G云计算第四章 LINUX Docker LNMP项目搭建一、项目环境1.环境描述2.容器ip地址规划3.任务需求 二、部署过程1.部署构建 nginx 镜像2.部署构建 mysql 镜像3.部署构建 php 镜像4.验证测试 计算机系统 5G云计算 第四章 LINUX Docker LNMP项目搭建 一、项目…...

数据包协议栈处理
看了两个不错的帖子,记录一下。 4.2 TCP Segmentation Offload(TSO)_Remy的学习记录-CSDN博客_tcp-segmentation-offload Linux内核参数之rp_filter - 萝卜1992 - 博客园...

html刷新图片
文章目录 前言网页整体刷新改变图像的url 备注 前言 海思3516的一个开发板,不断的采集图像编码为jpeg,保存为同一个文件。打算用网页实现查看视频的效果,需要前端能够自动刷新。 目前找到了两个方法,一个是网页的不断刷新&#…...

PHP反序列化漏洞之魔术方法
一、魔术方法 PHP魔术方法(Magic Methods)是一组特殊的方法,它们在特定的情况下会被自动调用,用于实现对象的特殊行为或提供额外功能。这些方法的名称都以双下划线开头和结尾,例如: __construct()、__toString()等。 …...
2023年的深度学习入门指南(20) - LLaMA 2模型解析
2023年的深度学习入门指南(20) - LLaMA 2模型解析 上一节我们把LLaMA 2的生成过程以及封装的过程的代码简单介绍了下。还差LLaMA 2的模型部分没有介绍。这一节我们就来介绍下LLaMA 2的模型部分。 这一部分需要一些深度神经网络的基础知识,不懂的话不用着急…...
智能安全配电装置应用场景有哪些?
安科瑞 华楠 一、应用背景 电力作为一种清洁能源,给人们带来了舒适、便捷的电气化生活。与此同时,由于使用不当,维护不及时等原因引发的漏电触电和电气火灾事故,也给人们的生命和财产带来了巨大的威胁和损失。 为了防止低压配电…...

Rust vs Go:常用语法对比(四)
题图来自 Go vs. Rust performance comparison: The basics 61. Get current date 获取当前时间 package mainimport ( "fmt" "time")func main() { d : time.Now() fmt.Println("Now is", d) // The Playground has a special sandbox, so you …...

c++ 派生类 文本查询程序再探
Query_base类和Query类 //这是一个抽象基类,具体的查询类型从中派生,所有成员都是private的 class Query_base {friend class Query;protected:using line_no TextQuery::line_no;//用于level函数virtual ~Query_base() default;private://eval返回与…...

17. 电话号码的字母组合
题目描述 给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。 示例 1: 输入:digits "23" …...

Redis 基础知识和核心概念解析:理解 Redis 的键值操作和过期策略
🌷🍁 博主 libin9iOak带您 Go to New World.✨🍁 🦄 个人主页——libin9iOak的博客🎐 🐳 《面试题大全》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~ἳ…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
