计算机科学cs/电子信息ei面试准备——数学基础/线性代数复习
1. 中值定理
中值定理是反映函数与导数之间联系的重要定理,也是微积分学的理论基础,在许多方面它都有重要的作用,在进行一些公式推导与定理证明中都有很多应用。中值定理是由众多定理共同构建的,其中拉格朗日中值定理是核心,罗尔定理是其特殊情况,柯西定理是其推广,还有泰勒定理。
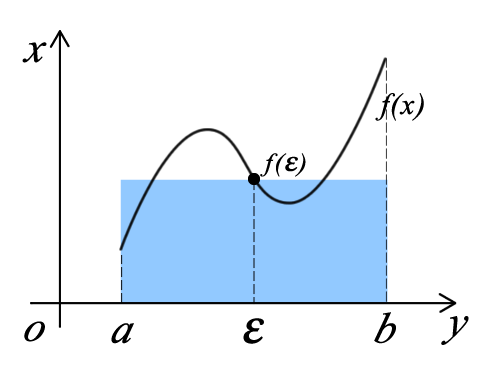
中值定理_百度百科
2. 梯度和散度
方向导数和梯度
标量场的梯度是一个矢量场!
这就是说,▽φ的模就是▽φ在给定点的最大方向导数,而其方向就是该具有最大方向导数的方向,亦即▽ φ的变化率最大的方向。 因此,我们定义标量场▽φ(x, y, z)在点P(x, y, z)处的梯度(gradient)为:
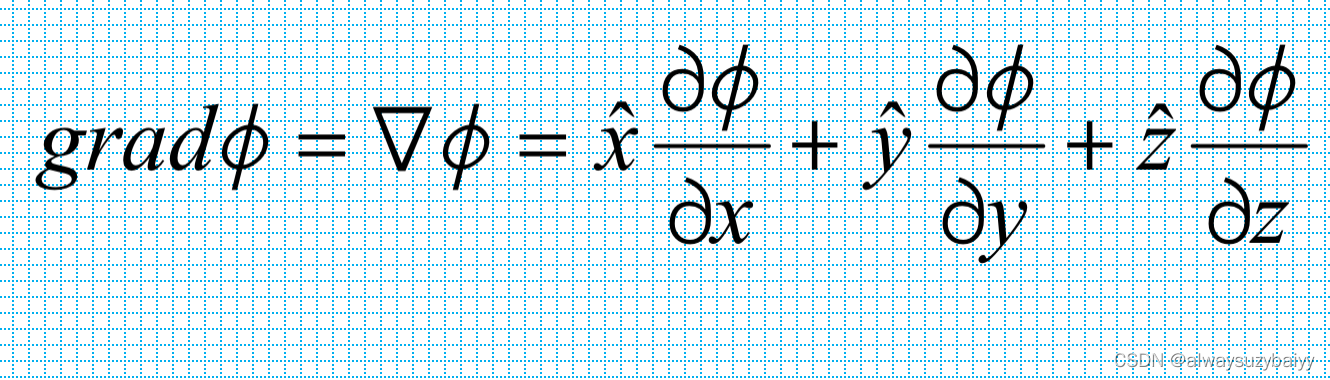
它是一个矢量,其模和方向就是标量场φ在该点最大变化率的值和方向。

即
后一式表明,梯度▽φ的方向与过该点的等值面相垂直,并由梯度定义知,它指向φ增大的方向。 由此,等值面的法线方向单位矢量可用梯度表示为
通量与散度
在描绘矢量场的特性时,矢量场穿过一个曲面的通量是一个很有用的概念。 在矢量分析中,将曲面的一个面元用矢量ds来表示,其方向取为面元的法线方向, 其大小为ds, 即
是面元的法线方向单位矢量。
的取法(指向)有两种情形: 对开曲面上的面元,设这个开曲面是由封闭曲线l所围成的,则当选定绕行l的方向后,沿绕行方向按右手螺旋的姆指方向就是
的方向,如图1 -4所示;对封闭曲面上的面元,
取为封闭面的外法线方向。
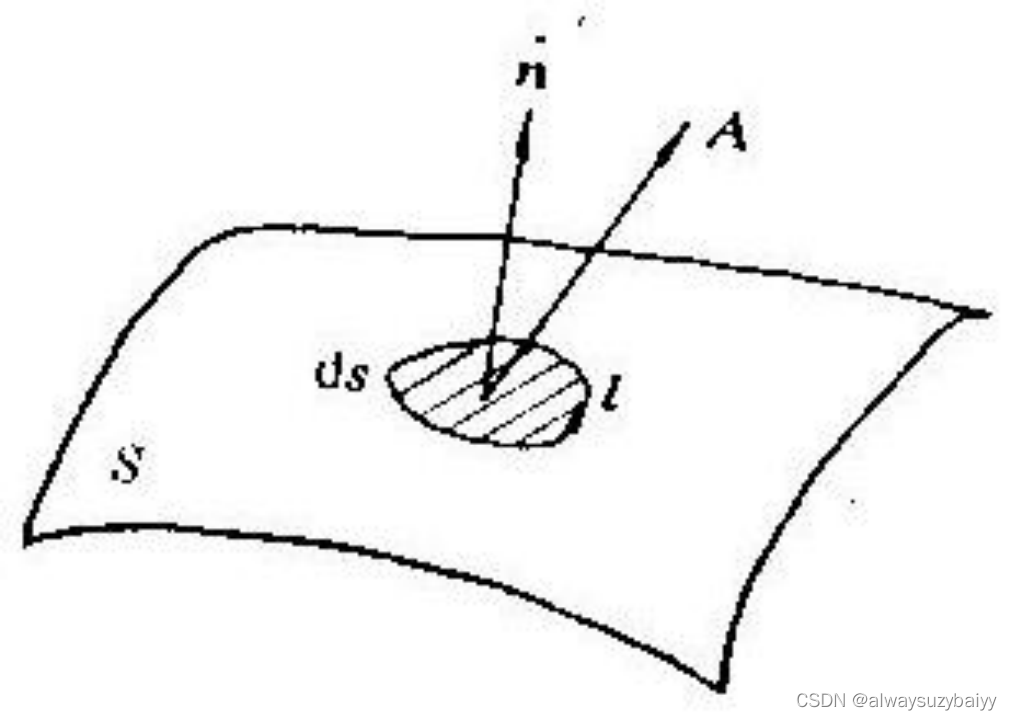
将曲面S各面元上的A·ds相加,它表示A穿过整个曲面S的通量,也称为A在曲面S上的面积分:
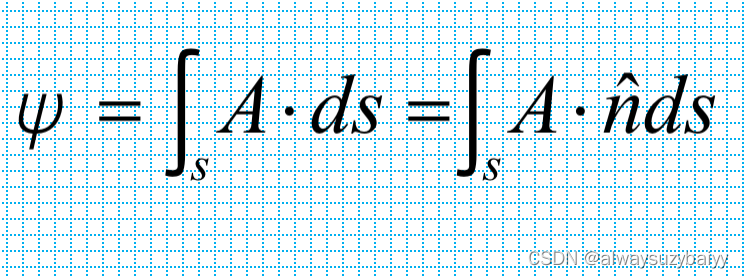
定义如下极限为矢量A在某点的散度(divergence),记为divA:
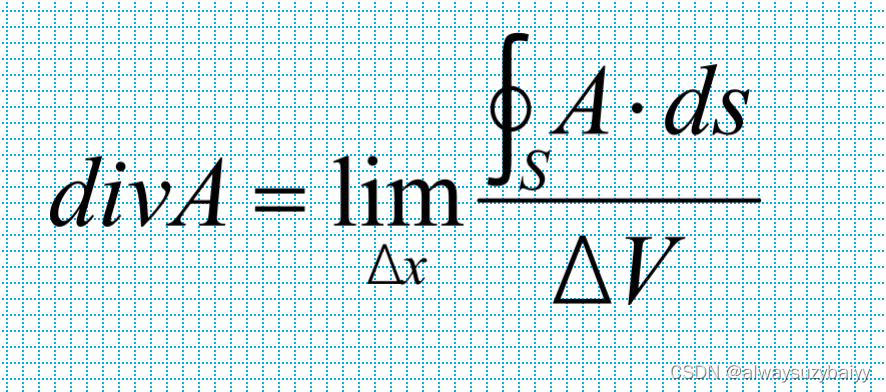
式中ΔV为封闭面S所包围的体积。 此式表明, 矢量A的散度是标量, 它是A通过某点处单位体积的通量(即通量体密度)。 它反映A在该点的通量源强度。 显然,在无源区中,A在各点的散度为零。 这个区域中的矢量场称为无散场或管形场。
A的散度可表示为算子与矢量A的标量积:
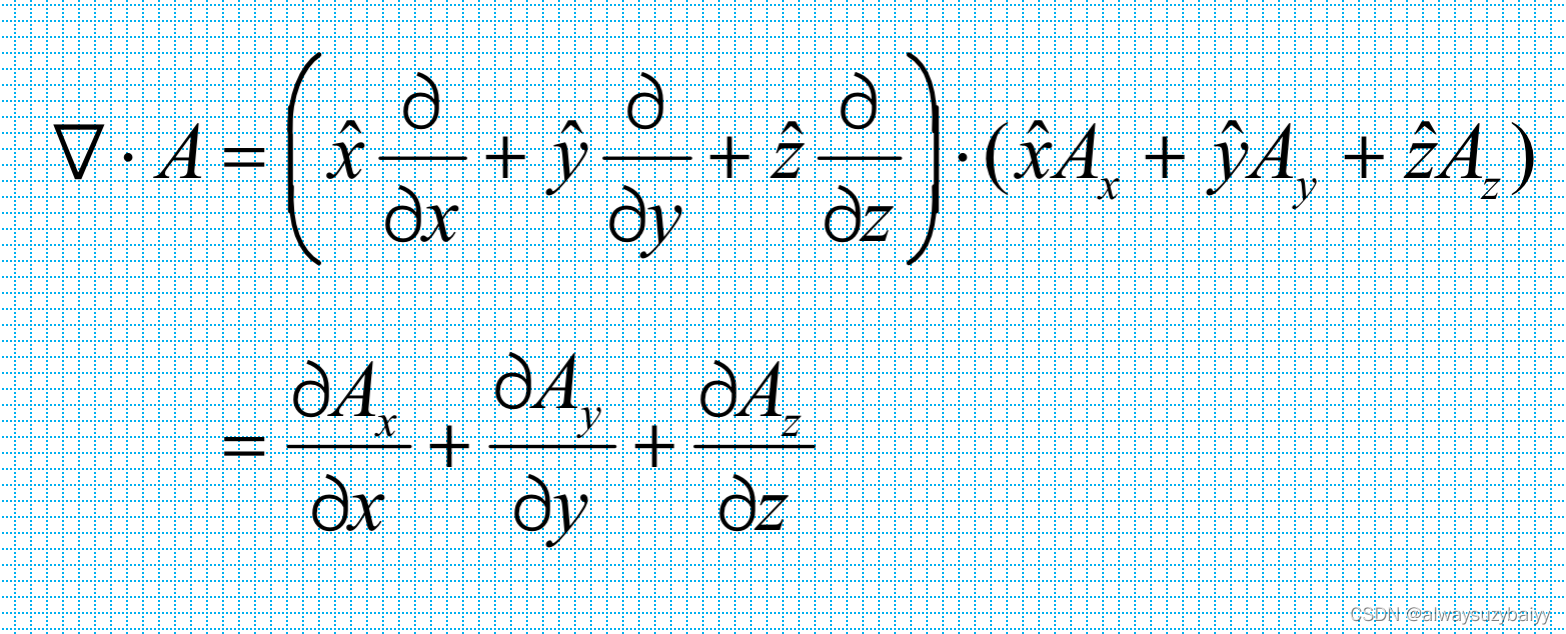
3. 泰勒公式是为了解决什么问题的?
泰勒公式:将函数展开为一个多项式与一个余项的和;
泰勒公式应用:
(1)应用泰勒中值定理(泰勒公式)可以证明中值等式或不等式命题。
(2)应用泰勒公式可以证明区间上的函数等式或不等式。
(3)应用泰勒公式可以进行更加精密的近似计算。(用多项式近似表示函数;)
(4)应用泰勒公式可以求解一些极限。
(5)应用泰勒公式可以计算高阶导数的数值。
它将一些复杂的函数逼近近似地表示为简单的多项式函数,泰勒公式这种化繁为简的功能,使得它成为分析和研究许多数学问题的有力工具。
常用的泰勒公式如下:
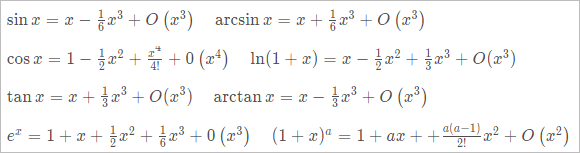
4. 矩阵的秩是什么,矩阵的秩物理意义?
矩阵的秩
矩阵的秩是线性代数中的一个概念。在线性代数中,一个矩阵A的列秩是A的线性独立的纵列的极大数,通常表示为r(A),rk(A)或rank A。类似地,行秩是A的线性无关的横行的极大数目。通俗一点说,如果把矩阵看成一个个行向量或者列向量,秩就是这些行向量或者列向量的秩,也就是极大无关组中所含向量的个数。
矩阵秩的物理意义
矩阵秩是线性代数中一个重要的概念,它描述了矩阵所包含的线性无关的列或行的数量。在物理学中,矩阵秩有着广泛的应用,特别是在矩阵分析、电路分析、力学和量子力学等领域。
在矩阵分析中,矩阵秩可以用来描述矩阵的性质和特征。例如,一个矩阵的秩为1,意味着它只有一个非零的列或行,这种矩阵通常被称为“秩一矩阵”。在物理学中,秩一矩阵通常用来描述一些特殊的物理现象,例如光的偏振、电磁波的传播和量子态的叠加等。
在电路分析中,矩阵秩可以用来描述电路的稳定性和可控性。例如,一个电路的秩为n,意味着它有n个独立的节点,这些节点可以被控制和测量。在物理学中,电路的秩可以用来描述电路的复杂性和可靠性,特别是在微电子学和通信领域。
在力学中,矩阵秩可以用来描述物体的运动和变形。例如,一个刚体的运动可以用一个6×6的矩阵来描述,其中前三行表示刚体的位置,后三行表示刚体的角度。这个矩阵的秩为6,意味着刚体的位置和角度是独立的,可以被分别控制和测量。在物理学中,矩阵秩可以用来描述物体的运动和变形,特别是在机械工程和航空航天领域。
在量子力学中,矩阵秩可以用来描述量子态的叠加和演化。例如,一个量子态可以用一个n×n的矩阵来描述,其中每个元素表示量子态的振幅。这个矩阵的秩为r,意味着量子态可以被分解为r个独立的态,每个态可以被控制和测量。在物理学中,矩阵秩可以用来描述量子态的叠加和演化,特别是在量子计算和量子通信领域。
矩阵秩是物理学中一个重要的概念,它可以用来描述物理现象的性质和特征。在不同的领域中,矩阵秩有着不同的应用和意义,但它们都反映了矩阵所包含的线性无关的列或行的数量。因此,矩阵秩是物理学中一个基础而又重要的概念,值得我们深入研究和探讨。
5. 特征值和特征向量的概念
A为n阶矩阵,若数λ和n维非0列向量x满足Ax=λx,那么数λ称为A的特征值,x称为A的对应于特征值λ的特征向量。式Ax=λx也可写成(A-λE)x=0,并且|λE-A|叫做A 的特征多项式。当特征多项式等于0的时候,称为A的特征方程,特征方程是一个齐次线性方程组,求解特征值的过程其实就是求解特征方程的解。
依据普通线性代数中的概念,特征值和特征向量能够用传统的方法求得,可是实际项目中一般都是用数值分析的方法来计算。
5.1 传统方法
定义1:设A是n阶方阵,若存在数和非零向量
,
使得
则称是A的一个特征值,
x为A的对应于特征值的特征向量。

为矩阵A的特征多项式,记作

推论 n阶方阵A可逆的充要条件是A的n个特征值非零
即利用特征多项式可以求出所有的特征值,特征值之和等于原矩阵对角线元素之和,特征值的乘积等于原矩阵A的行列式的值。
特征多项式的乘积等于矩阵之积。
例题
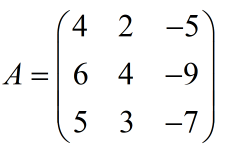
计算:A的特征值和特征向量。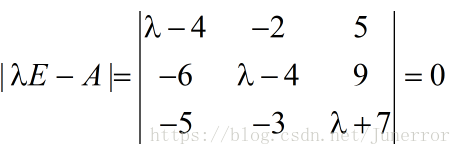

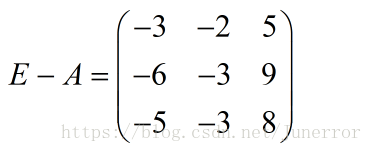
=
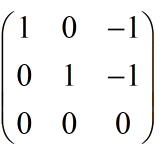
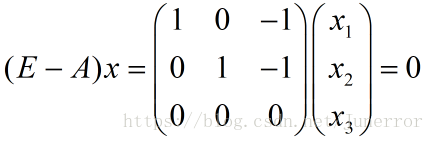
令x=1,便可得出一个基础解系:
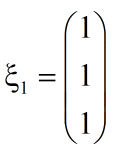
同理当时,得出:
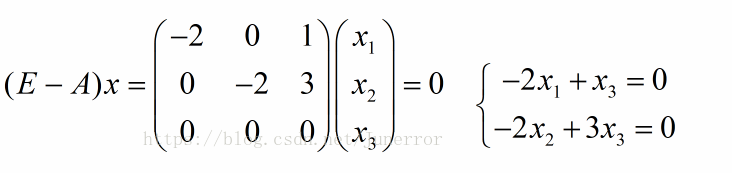
同样可以得出特征向量
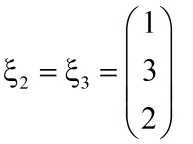
5.2 雅可比迭代法
雅可比方法用于求实对称矩阵的所有特征值、特征向量。Jacobi算法计算简单、稳定性好、精度高、求得的特征向量正交性好。但当A为稀疏阵时,Givens旋转变换将破坏其稀疏性,且只能适用于实对称矩阵。
6. 什么是线性相关以及线性相关的性质?
7. 中心极限定理以及它的研究意义是什么?
相关文章:
计算机科学cs/电子信息ei面试准备——数学基础/线性代数复习
1. 中值定理 中值定理是反映函数与导数之间联系的重要定理,也是微积分学的理论基础,在许多方面它都有重要的作用,在进行一些公式推导与定理证明中都有很多应用。中值定理是由众多定理共同构建的,其中拉格朗日中值定理是核心&…...
-算法分析)
极速查找(2)-算法分析
篇前小言 本篇文章是对查找(1)的续讲线性索引查找 线性索引查找(Linear Index Search)是一种基于索引的查找算法。它在数据集合中创建一个索引 结构,然后使用该索引结构来加快对目标元素的查找。 线性索引是一种在数…...

flask路由添加参数
flask路由添加参数 在 Flask 中,可以通过两种方式在路由中添加参数:在路由字符串中直接指定参数,或者通过 request 对象从请求中获取参数。 在路由字符串中指定参数:可以将参数直接包含在路由字符串中。参数可以是字符串、整数、…...

网络安全系统教程+学习路线(自学笔记)
一、什么是网络安全 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防两面…...

23. 合并 K 个升序链表
题目描述 给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合并后的链表。 示例 1: 输入:lists [[1,4,5],[1,3,4],[2,6]] 输出:[1,1,2,3,4,4,5,6] 解释:链表数组…...
Nexus3部署、配置+SpringBoot项目Demo
Docker部署Nexus 搜索Nexus3镜像:[rootlocalhost ~]# docker search nexus 拉取Nexus3镜像:[rootlocalhost ~]# docker pull sonatype/nexus3 启动Nexus3前查看虚拟机端口是否被占用:[rootlocalhost ~]# netstat -nultp 通过Docker Hub查看安…...
linux下用docker安装mysql
1.mysql Docker镜像 docker pull mysql:[版本号 或 latest]例:docker pull mysql:5.7 2.查看拉取的docker镜像 docker images3.设置 Docker 卷 docker volume create mysql-data列出 Docker 已知的所有卷 docker volume ls4.运行一个 MySQL Docker 容器 docke…...
Vue - 可视化用户角色、菜单权限、按钮权限配置(动态获取菜单路由)
GitHub Demo 地址 在线预览 前言 关于动态获取路由已在这里给出方案 Vue - vue-admin-template模板项目改造:动态获取菜单路由 这里是在此基础上添加了系统管理模块,包含用户管理,角色管理,菜单管理,字典管理…...

hive库操作示例
hive库操作示例 1、常规表 创建数据库 CREATE DATABASE mydatabase;使用数据库 USE mydatabase;创建表 CREATE TABLE mytable (id INT,name STRING,age INT ) ROW FORMAT DELIMITED FIELDS TERMINATED BY , STORED AS TEXTFILE;插入数据 INSERT INTO TABLE mytable VALUE…...
LeetCode第 N 个泰波那契数 (认识动态规划)
认识动态规划 编写代码代码空间优化 链接: 第 N 个泰波那契数 编写代码 class Solution { public:int tribonacci(int n) {if(n 0){return 0;}else{if(n 1 || n 2)return 1;}vector<int> dp(n 1);dp[0] 0;dp[1] 1;dp[2] 1;for(int i 3;i < n;i){dp[i] dp[i-3]…...
)
线程安全问题(内存可见性)
导致的原因 内存可见性问题的出现主要是因为编译器优化多线程导致的 示例代码 package 线程安全问题;import java.util.Scanner;/*** Created with IntelliJ IDEA.* Description:* User: wuyulin* Date: 2023-07-26* Time: 13:49*/ public class Demo2 {private volatile sta…...
STM32MX配置EEPROM(AT24C02)------保姆级教程
———————————————————————————————————— ⏩ 大家好哇!我是小光,嵌入式爱好者,一个想要成为系统架构师的大三学生。 ⏩最近在开发一个STM32H723ZGT6的板子,使用STM32CUBEMX做了很多驱动&#x…...
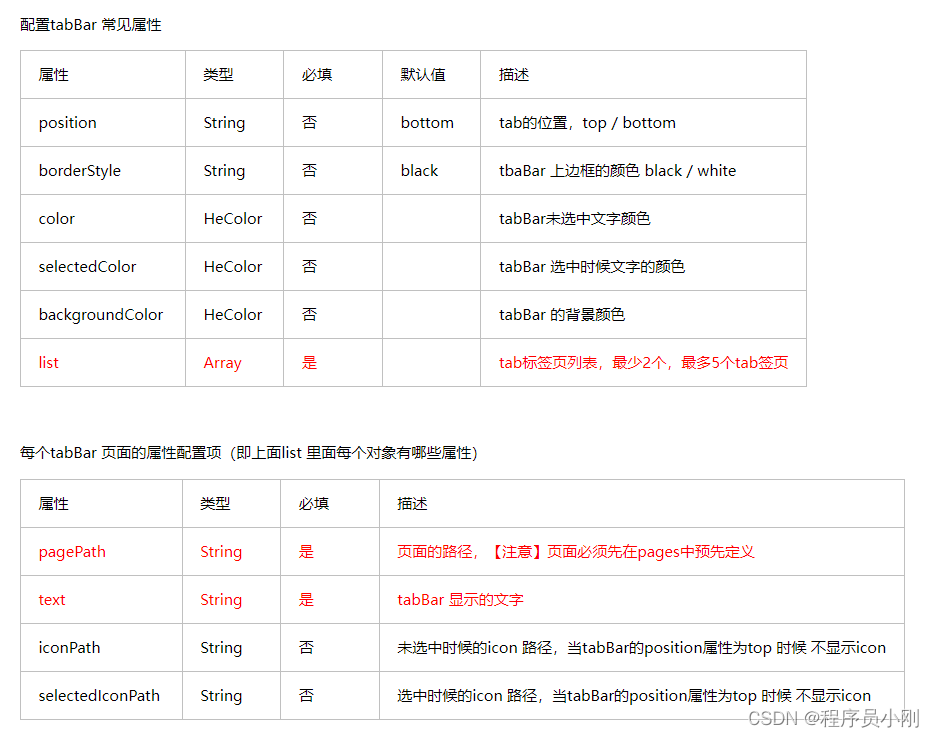
微信小程序 样式和全局配置
WXSS wxss 把屏幕分为750个物理像素,大屏大,小屏小,随着设备不一致自动适配 推荐使用iPhone6作为标准,1个rpx 0.5个px,把px乘以2就是rpx的参数 import 导入外部样式表 import /common/common.wxss 样式 权重一…...

一.初识C语言
一.初识C语言 C语言标准规定: sizeof(long)>sizeof(int)就可以了变量要定义在当前代码块的最前面 #defin _CRT_SECURE_NO_WARNINGS 1#include <stdio.h> //包含一个stdio.h的文件 std-标准standard input outputint main() //主函数-程序的入口-main函数…...

filebeat到kafka示例
docker run -d \ --namefilebeat_7.14_0 \ #filebeat名称 --userroot \ --volume"/data/filebeat/filebeat.yml:/usr/share/filebeat/filebeat.yml" \ #映射filebeat.yml配置 --volume"/data/filebeat/log:/usr/share/filebeat/log" \…...

AlmaLinux系统下的Zabbix汉化
我安装的是zabbix下的虚拟机,安装完成后,直接可以打开网站了,但是界面是英文,看了设置,没有中文选项,就需要在系统中安装中文字符集了。 # locale -a #查看里面没有zh_CN之类的项 # dnf install -…...
【网络编程】(TCP流套接字编程 ServerSocket API Socket API 手写TCP版本的回显服务器 TCP中的长短连接)
文章目录 网络编程TCP流套接字编程ServerSocket APISocket APITCP中的长短连接手写TCP版本的回显服务器 网络编程 TCP流套接字编程 TCP提供的API主要是两个类:ServerSocket 和 Socket . TCP不需要一个类来表示"TCP数据报"因为TCP不是以数据报为单位进行传输的.是以…...
企业级PaaS低代码快开平台源码,基于 Salesforce Platform 的开源替代方案
PaaS低代码快开平台是一种快速开发应用系统的工具,用户通过少量代码甚至不写代码就可以快速构建出各种应用系统。 随着信息化技术的发展,企业对信息化开发的需求正在逐渐改变,传统的定制开发已经无法满足企业需求。低代码开发平台࿰…...

【LeetCode】72.编辑距离
题目 给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。 你可以对一个单词进行如下三种操作: 插入一个字符删除一个字符替换一个字符 示例 1: 输入:word1 "horse", word2 "…...
大模型,开源干不掉闭源
开源大模型对闭源大模型的冲击,变得非常猛烈。 今年3月,Meta发布了Llama(羊驼),很快成为AI社区内最强大的开源大模型,也是许多模型的基座模型。有人戏称,当前的大模型集群,就是一堆各…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...

Android写一个捕获全局异常的工具类
项目开发和实际运行过程中难免会遇到异常发生,系统提供了一个可以捕获全局异常的工具Uncaughtexceptionhandler,它是Thread的子类(就是package java.lang;里线程的Thread)。本文将利用它将设备信息、报错信息以及错误的发生时间都…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...
