【算法基础:搜索与图论】3.4 求最短路算法(Dijkstrabellman-fordspfaFloyd)
文章目录
- 求最短路算法总览
- Dijkstra
- 朴素 Dijkstra 算法(⭐原理讲解!⭐重要!)(用于稠密图)
- 例题:849. Dijkstra求最短路 I
- 代码1——使用邻接表
- 代码2——使用邻接矩阵
- 补充:稠密图和稀疏图 & 邻接矩阵和邻接表
- 堆优化版Dijkstra算法(⭐原理讲解!⭐重要!)用于稀疏图
- 例题:850. Dijkstra求最短路 II
- bellman-ford
- 例题:853. 有边数限制的最短路
- 为什么需要对 dis 数组进行备份?
- spfa算法(bellman-ford 算法的优化)
- 例题:851. spfa求最短路
- 例题:852. spfa判断负环
- Floyd(很暴力的三重循环)
- 例题:854. Floyd求最短路
求最短路算法总览
关于最短路可见:https://oi-wiki.org/graph/shortest-path/

无向图 是一种 特殊的 有向图。(所以上面的知识地图上没有区分边有向还是无向)
关于存储:稠密图用邻接矩阵,稀疏图用邻接表。
朴素Dijkstra 和 堆优化Dijkstra算法的 选择就在于图 是 稠密的还是稀疏的。
Dijkstra
朴素 Dijkstra 算法(⭐原理讲解!⭐重要!)(用于稠密图)
算法步骤:
有一个集合 s 存储当前已经确定是最短距离的点。
- 初始化距离,dis[1] = 0, dis[i] = +∞
- for i: 1 ~ n 。 (每次循环确定一个点到起点的最短距离,这样 n 次循环就可以确定 n 个点的最短距离)
找到不在 s 中的 距离最近的点 t,将其放入 s 中。
用 t 来更新其它所有点的距离(检查所有从 t 出发可以到达的点 x,是否有 dis[x] > dis[t] + w)

例题:849. Dijkstra求最短路 I
https://www.acwing.com/activity/content/problem/content/918/
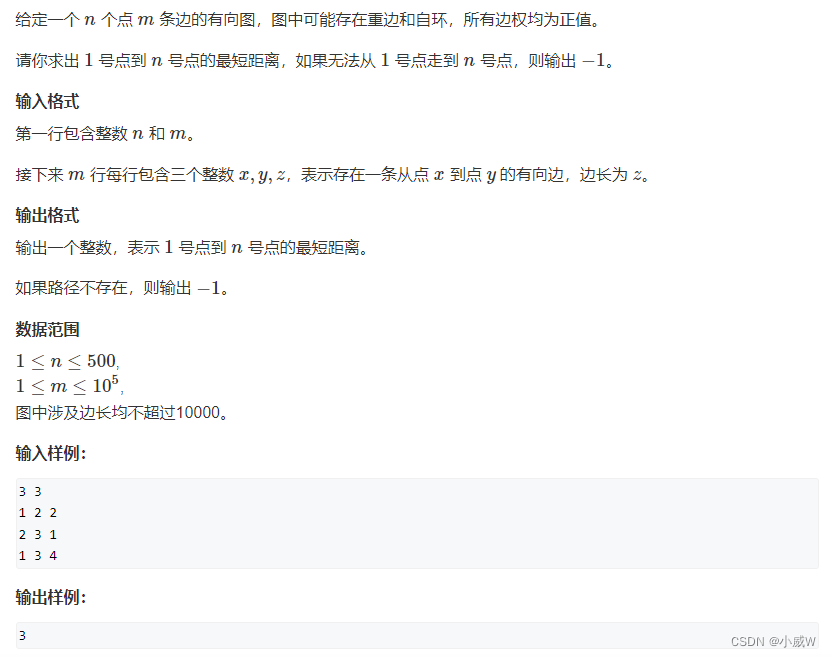
注意图是有向图,图中可能存在重边和自环,所有边权为正值。
求从 1 号点到 n 号点 的最短距离。
按照朴素 Dijkstra 算法的原理,每次用当前不在 s 中的最短距离节点 t 更新其它所有 t 可以到达的下一个节点,重复这个过程 n 次就可以确定 n 个节点的最短距离。
代码1——使用邻接表
import java.util.*;public class Main {public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt();// 建图List<int[]>[] g = new ArrayList[n + 1];Arrays.setAll(g, e -> new ArrayList<>());for (int i = 0; i < m; ++i) {int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();g[x].add(new int[]{y, z});}// 初始化距离int[] dis = new int[n + 1];Arrays.fill(dis, Integer.MAX_VALUE);dis[1] = 0;boolean[] st = new boolean[n + 1];for (int i = 1; i < n; ++i) {int t = -1;// 找到当前不在 s 中的最短距离 t 的位置for (int j = 1; j <= n; ++j) {if (!st[j] && (t == -1 || dis[j] < dis[t])) t = j;}if (t == n) break; // 当前离得最近的就是 n 了,直接返回st[t] = true;// 使用 t 更新所有从 t 出发可以达到的下一个节点for (int[] y: g[t]) dis[y[0]] = Math.min(dis[y[0]], dis[t] + y[1]);}if (dis[n] == Integer.MAX_VALUE) System.out.println("-1");else System.out.println(dis[n]);}
}
代码2——使用邻接矩阵
从题目中可以看出是稠密图,所以使用邻接矩阵效率会更高一些。
import java.util.*;public class Main {public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt();// 建图 g[i][j]表示从i到j的距离int[][] g = new int[n + 1][n + 1];for (int[] ints : g) Arrays.fill(ints, 0x3f3f3f3f);for (int i = 0; i < m; ++i) {int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();g[x][y] = Math.min(g[x][y], z);}// 初始化各个点到起始点的距离int[] dis = new int[n + 1];Arrays.fill(dis, Integer.MAX_VALUE);dis[1] = 0;boolean[] st = new boolean[n + 1];for (int i = 1; i < n; ++i) {int t = -1;// 找到当前不在 s 中的最短距离 t 的位置for (int j = 1; j <= n; ++j) {if (!st[j] && (t == -1 || dis[j] < dis[t])) t = j;}if (t == n) break; // 当前离得最近的就是 n 了,直接返回st[t] = true;// 使用 t 更新所有从 t 出发可以达到的下一个节点for (int j = 1; j <= n; ++j) {dis[j] = Math.min(dis[j], dis[t] + g[t][j]);}}if (dis[n] == 0x3f3f3f3f) System.out.println("-1");else System.out.println(dis[n]);}
}补充:稠密图和稀疏图 & 邻接矩阵和邻接表

总结一下:
邻接矩阵的空间复杂度为 O ( n 2 ) O(n^2) O(n2),邻接表的空间复杂度为 O ( n + m ) O(n + m) O(n+m),其中 n 是图中节点的数量,m 是边的数量。
Q:如何判断什么时候是稠密的?
A:当 m m m 接近最大可能边数 n ∗ ( n − 1 ) / 2 n * (n - 1)/2 n∗(n−1)/2 时,那么图通常被视为稠密的。
堆优化版Dijkstra算法(⭐原理讲解!⭐重要!)用于稀疏图
如果是一个稀疏图, O ( n 2 ) O(n^2) O(n2) 的朴素 Dijkstra 算法可能会很慢,因此出现了堆优化版本的 Dijkstra 算法。

用堆来存储所有点到起点的最短距离,就可以减小整个算法的时间复杂度。
用 t 更新其它点的距离,因为有 m 条边,所以这个操作是 m 次,每次的时间复杂度是 logn,因此一共是 m ∗ log n m*\log{n} m∗logn。 (所以 m 比较小时,即稀疏图,使用堆优化效果更好)
其实就是用堆来优化了每次找当前和起始点最近的点的过程。(朴素的需要枚举 n)
例题:850. Dijkstra求最短路 II
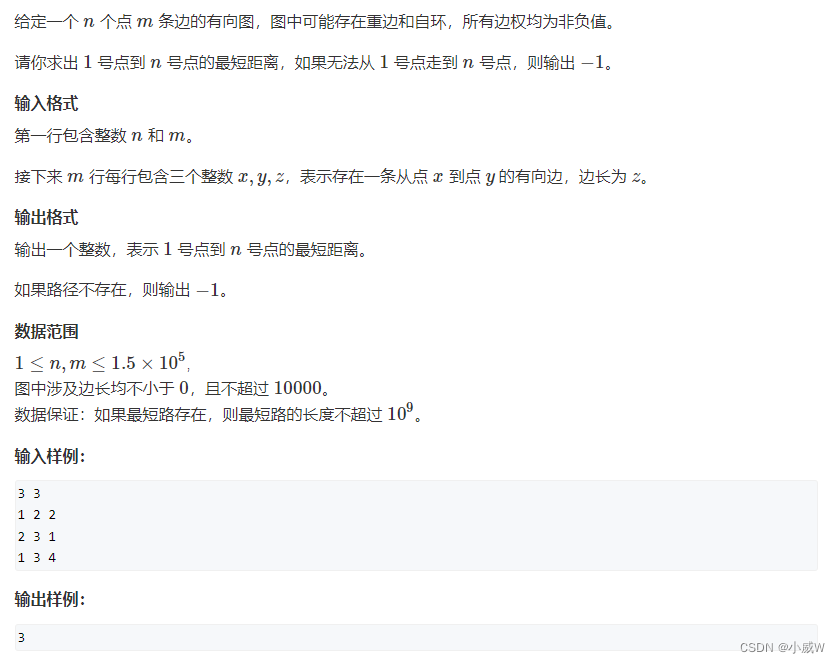
https://www.acwing.com/activity/content/problem/content/919/
import java.util.*;public class Main {public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt();// 建图List<int[]>[] g = new ArrayList[n + 1];Arrays.setAll(g, e -> new ArrayList<int[]>());for (int i = 0; i < m; ++i) {int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();g[x].add(new int[]{y, z});}//int[] dis = new int[n + 1];Arrays.fill(dis, 0x3f3f3f3f);dis[1] = 0;boolean[] st = new boolean[n + 1];// 按照各个节点与初始节点之间距离 从小到大 排序PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);pq.offer(new int[]{1, 0});while (!pq.isEmpty()) {int[] cur = pq.poll();int x = cur[0], d = cur[1];if (st[x]) continue; // 检查这个节点是否已经用来更新过了st[x] = true;// 只要被当前节点更新了就放入优先队列中for (int[] y: g[x]) { // 这个循环最多被执行 m 次(因为有 m 条边)if (dis[y[0]] > d + y[1]) {dis[y[0]] = d + y[1];pq.offer(new int[]{y[0], dis[y[0]]});}}}System.out.println(dis[n] == 0x3f3f3f3f? -1: dis[n]);;}
}bellman-ford
枚举 n 次:每次 循环所有边 a, b, wdis[b] = min(dis[b], dis[a] + w)
循环完之后, 所有节点会满足 dis[b] <= dis[a] + w。

对于 n 次循环中的第 k 次循环,求出的是 : 从 起点走 不超过 k 条边 的最短距离。
因此 如果第 n 次循环时有更新,说明图中存在负环。
例题:853. 有边数限制的最短路
https://www.acwing.com/problem/content/description/855/

注意! : 如果有负权回路,那么最短路就一定不存在了!
bellman-ford 算法可以判断出 图中是否存在负权回路。(但是一般使用 spfa 来判断是否有负环)
Q:这道题为什么必须使用 bellman-ford 算法?
A:因为限制了最多经过 k 条边,即存在边数限制。
import java.util.*;public class Main {public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt(), k = scanner.nextInt();// 存储所有边int[][] edges = new int[m][3];for (int i = 0; i < m; ++i) {edges[i][0] = scanner.nextInt();edges[i][1] = scanner.nextInt();edges[i][2] = scanner.nextInt();}int[] dis = new int[n + 1], last;Arrays.fill(dis, 0x3f3f3f3f);dis[1] = 0;// 限制 k 次。 (k 次就表示最多经过 k 条边)for (int i = 0; i < k; ++i) {last = Arrays.copyOf(dis, n + 1); // 将dis数组先备份一下for (int j = 0; j < m; ++j) { // 枚举所有边dis[edges[j][1]] = Math.min(dis[edges[j][1]], last[edges[j][0]] + edges[j][2]);}}// 因为存在负权边,而本题的数据范围最多减 500 * 10000。所以和 0x3f3f3f3f/2 比较大小System.out.println(dis[n] > 0x3f3f3f3f / 2? "impossible": dis[n]);}
}为什么需要对 dis 数组进行备份?
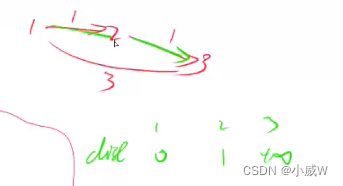
因为如果不备份的话可能会发生串联,为了避免串联,每次更新时只用上一次的结果。
比如上图,在第一次循环中 2 的 dis 被更新成了 1,如果不使用备份的话,那么 3 的 dis 会被接着更新为 2,但这并不是我们所期望的, 3 的 dis 被更新成 2 应该是在第 2 次循环时才会发生的事情。
spfa算法(bellman-ford 算法的优化)
相当于对 bellman-ford 算法做了一个优化。
bellman-ford 在每次循环中枚举了所有边,但实际上有些边并不会对松弛有作用,所以 spfa 就是从这一点进行了优化。
(使用队列宽搜进行优化)。
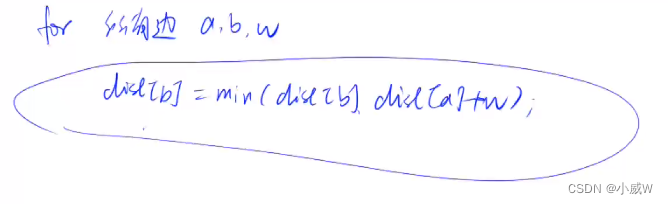
从公式 d i s [ b ] = m i n ( d i s [ b ] , d i s [ a ] + w ) dis[b] = min(dis[b], dis[a] + w) dis[b]=min(dis[b],dis[a]+w) 可以看出,只有当 d i s [ a ] dis[a] dis[a] 变小了,这条边才有可能让 d i s [ b ] dis[b] dis[b] 跟着变小。
算法步骤:

基本思想:只有我变小了,我后面的人才会跟着变小。
队列里面存的是待更新的点,就是等着用来更新其它点的点。
例题:851. spfa求最短路
https://www.acwing.com/activity/content/problem/content/920/
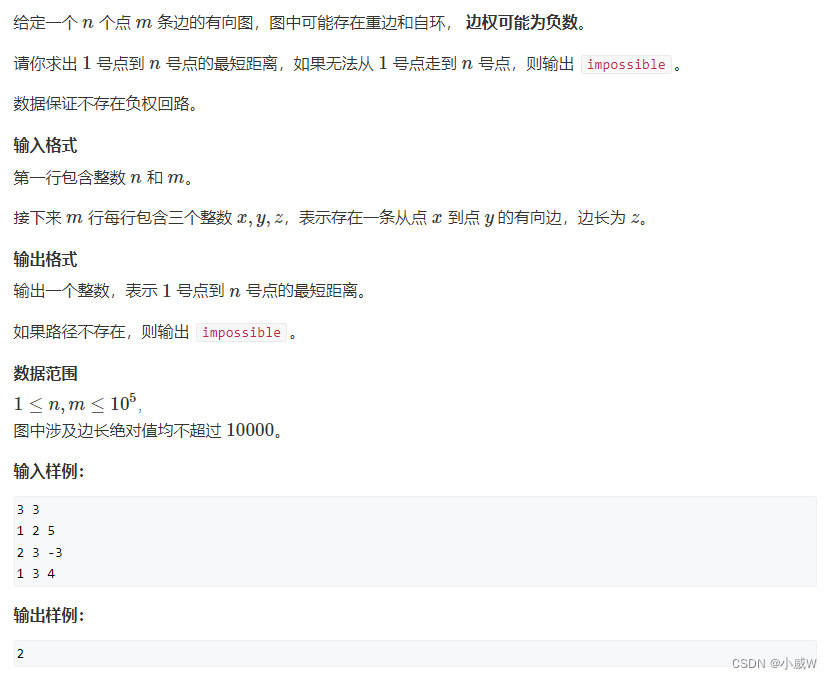
这一题的数据保证了图中不存在负环。
代码中不再是 n 次循环嵌套 m 次循环的 bellman-ford 算法了,
而是一个队列维护可以用来更新其它节点的节点队列,初始时放入起始节点 1,其余时间每次取出队首的节点即可。
取出一个节点后,枚举它影响的所有其它节点即可,如果其它节点被影响了,就表示可以把这个被影响的节点放入队列中,(不过放进队列之前要先判断一下是否已经在队列中了,防止重复更新)。
import java.util.*;public class Main {public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt();// 使用邻接表存储List<int[]>[] g = new ArrayList[n + 1];Arrays.setAll(g, e -> new ArrayList<int[]>());for (int i = 0; i < m; ++i) {g[scanner.nextInt()].add(new int[]{scanner.nextInt(), scanner.nextInt()});}// 初始化距离、队列、是否在队列里的状态int[] dis = new int[n + 1];Arrays.fill(dis, 0x3f3f3f3f);dis[1] = 0;Queue<Integer> q = new LinkedList<Integer>();q.offer(1);boolean[] st = new boolean[n + 1];st[1] = true;while (!q.isEmpty()) {int t = q.poll();st[t] = false;for (int[] y: g[t]) {int j = y[0], w = y[1];if (dis[j] > dis[t] + w) {dis[j] = dis[t] + w;// 由于 j 变小了,所以它可以被更新,可以放入队列中// 但是放进去之前要先判断已经是否已经在队列中了,防止重复放置if (!st[j]) {q.offer(j);st[j] = true;}}}}System.out.println(dis[n] == 0x3f3f3f3f? "impossible": dis[n]);}
}
例题:852. spfa判断负环
https://www.acwing.com/problem/content/description/854/
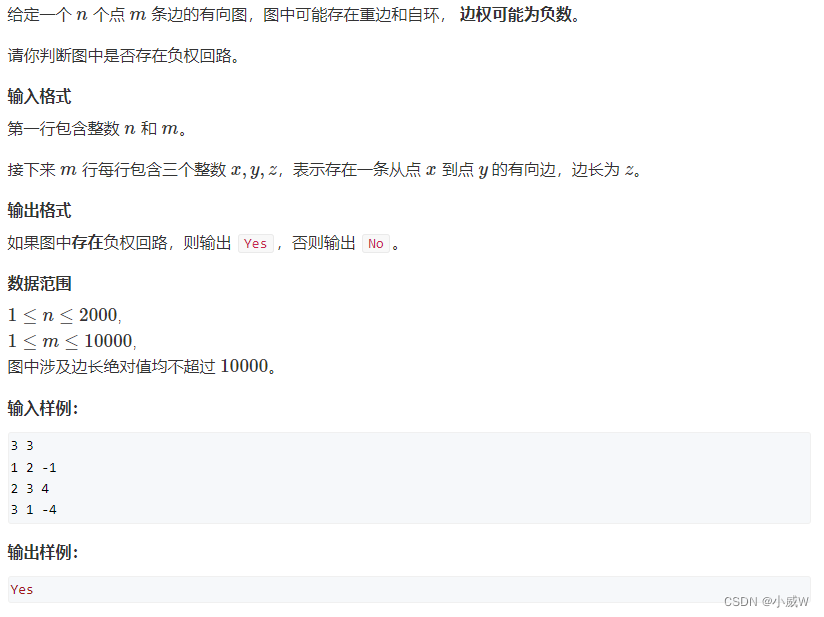
跟 bellman-ford 算法判断负环的思路差不多,在更新 dis 数组的同时,维护一个 cnt 数组,cnt[x] 表示当前这个最短路的经过的边数。
每次更新 dis[x] 的时候,就把 cnt[x] 更新成 cnt[t] + 1。(因为 x 是从节点 t 更新过来的)。
如果在更新的过程中出现了 cnt[x] >= n,就表示至少经过了 n 条边,即至少经过了 n + 1 个点,这肯定是不合理的,说明存在负环。
import java.util.*;public class Main {public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt();// 使用邻接表存储List<int[]>[] g = new ArrayList[n + 1];Arrays.setAll(g, e -> new ArrayList<int[]>());for (int i = 0; i < m; ++i) {g[scanner.nextInt()].add(new int[]{scanner.nextInt(), scanner.nextInt()});}System.out.println(spfa(g, n)? "Yes": "No");}static boolean spfa(List<int[]>[] g, int n) {// 初始化距离、队列、是否在队列里的状态int[] dis = new int[n + 1], cnt = new int[n + 1];Arrays.fill(dis, 0x3f3f3f3f);dis[1] = 0;boolean[] st = new boolean[n + 1];Queue<Integer> q = new LinkedList<Integer>();// 是判断是否存在负环,而不是只判断从1开始是否存在负环for (int i = 1; i <= n; ++i) {q.offer(i);st[i] = true;}while (!q.isEmpty()) {int t = q.poll();st[t] = false;for (int[] y: g[t]) {int j = y[0], w = y[1];if (dis[j] > dis[t] + w) {dis[j] = dis[t] + w;cnt[j] = cnt[t] + 1;if (cnt[j] >= n) return true; // 表示有负环// 由于 j 变小了,所以它可以被更新,可以放入队列中// 但是放进去之前要先判断已经是否已经在队列中了,防止重复放置if (!st[j]) {q.offer(j);st[j] = true;}}}}return false; // false表示没有负环}
}
Floyd(很暴力的三重循环)
https://oi-wiki.org/graph/shortest-path/#floyd-%E7%AE%97%E6%B3%95
用于求多源汇最短路。可以求任意两个结点之间的最短路。
使用邻接矩阵将原图存储下来,三重循环。
d[i][j]for (int k = 1; k <= n; ++k) {for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {// 看看i直接到j更近还是 经过k之后更近d[i][j] = min(d[i][j], d[i][k] + d[k][j]); }}
}
原理其实是基于:动态规划
例题:854. Floyd求最短路
https://www.acwing.com/problem/content/856/

题目数据保证了不存在负权回路。
同样要注意最后各个距离要和 INF / 2 比较而不是和 INF 比较,因为图中可能存在负权。
import java.util.*;public class Main {public static void main(String[] args){Scanner scanner = new Scanner(System.in);int n = scanner.nextInt(), m = scanner.nextInt(), t = scanner.nextInt(), INF = (int)1e9;// 建图int[][] g = new int[n + 1][n + 1];for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {if (i == j) g[i][j] = 0;else g[i][j] = INF;}}for (int i = 0; i < m; ++i) {int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();g[x][y] = Math.min(g[x][y], z);}// 求多源最短路for (int k = 1; k <= n; ++k) {for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);}}}// 回答询问while (t-- != 0) {int x = scanner.nextInt(), y = scanner.nextInt();System.out.println(g[x][y] > INF / 2? "impossible": g[x][y]); // 由于有负权,所以和INF/2比较}}
}
相关文章:

【算法基础:搜索与图论】3.4 求最短路算法(Dijkstrabellman-fordspfaFloyd)
文章目录 求最短路算法总览Dijkstra朴素 Dijkstra 算法(⭐原理讲解!⭐重要!)(用于稠密图)例题:849. Dijkstra求最短路 I代码1——使用邻接表代码2——使用邻接矩阵 补充:稠密图和稀疏…...
)
【Matlab】基于卷积神经网络的数据分类预测(Excel可直接替换数据)
【Matlab】基于卷积神经网络的数据分类预测(Excel可直接替换数据) 1.模型原理2.数学公式3.文件结构4.Excel数据5.分块代码6.完整代码7.运行结果1.模型原理 基于卷积神经网络(Convolutional Neural Network,CNN)的数据分类预测是一种常见的深度学习方法,广泛应用于图像识…...

【C++ 重要知识点总结】自定义类型-枚举和联合
复杂类型 除了类之外还有Union、Enum连个特殊的类型。 Union 概念 union即为联合,它是一种特殊的类。通过关键字union进行定义,一个union可以有多个数据成员。 union Token{char cval;int ival;double dval; };用法 互斥赋值。在任意时刻,…...

Centos MySql安装,手动安装保姆级教程
1.删除原有的mariadb,不然mysql装不进去 查询MAriaDB命令 rpm -qa|grep mariadb 删除 rpm -e --nodeps mariadb-libs-5.5.60-1.el7_5.x86_64 (yum -y remove mysql 如需要清除服务器上以前安装过的MySQL可执行此命令,执行前一…...
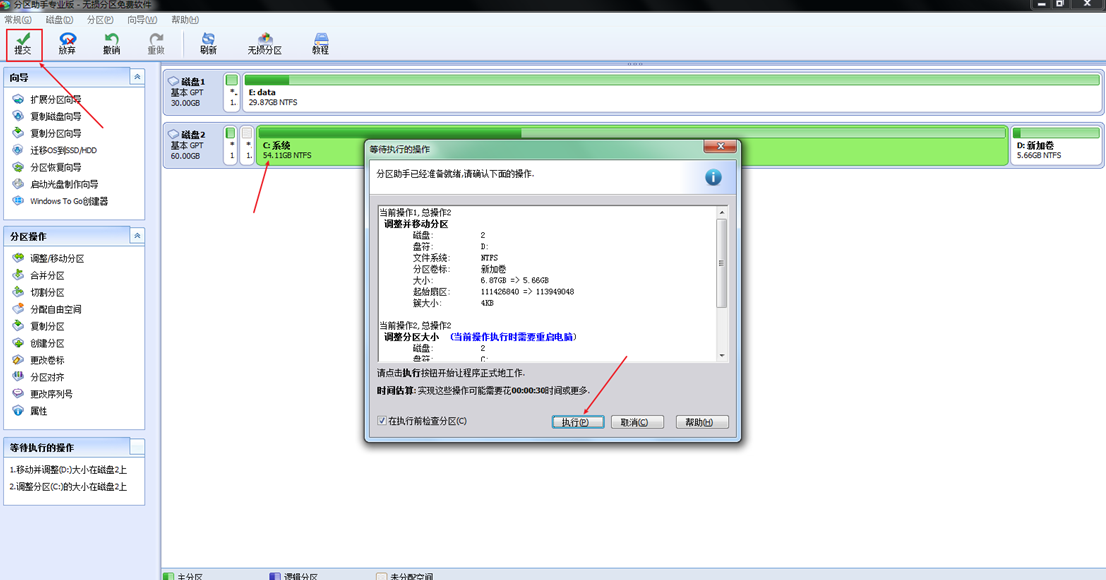
电脑C盘空间大小调整 --- 扩容(扩大/缩小)--磁盘分区大小调整/移动
概述: 此方法适合C盘右边没有可分配空间(空闲空间)的情况,D盘有数据不方便删除D盘分区的情况下,可以使用傲梅分区助手软件进行跨分区调整分区大小,不会损坏数据。反之可直接使用系统的磁盘管理工具进行调整…...

centos7设置网桥网卡
安装bridge-utils yum install bridge-utils修改ens33 网卡 TYPEEthernet BOOTPROTOnone DEFROUTEyes IPV4_FAILURE_FATALno IPV6INITyes IPV6_AUTOCONFyes IPV6_DEFROUTEyes IPV6_FAILURE_FATALno NAMEens33 UUID04b97484-25c8-45c7-8c8c-e335e8080e10 DEVICEens33 ONBOOTye…...

TCP模型和工作沟通方式
我们如何与客户沟通?理科生和技术人员可能在沟通技巧方面有所欠缺。 那么我们如何理解和掌握沟通的原则和技巧呢?我发现TCP网络交互模型很好的描述了沟通的原则和要点。下面我们就从TCP来讲沟通的过程。 TCP的客户端就像客户(甲方ÿ…...

Langchain 的 ConversationSummaryBufferMemory
Langchain 的 ConversationSummaryBufferMemory ConversationSummaryBufferMemory 在内存中保留最近交互的缓冲区,但不仅仅是完全刷新旧的交互,而是将它们编译成摘要并使用两者。但与之前的实现不同的是,它使用令牌长度而不是交互次数来确定何…...

【Rust 基础篇】Rust 通道实现单个消费者多个生产者模式
导言 在 Rust 中,我们可以使用通道(Channel)来实现单个消费者多个生产者模式,简称为 MPMC。MPMC 是一种常见的并发模式,适用于多个线程同时向一个通道发送数据,而另一个线程从通道中消费数据的场景。本篇博…...

HTTP协议各版本介绍
HTTP协议是一种用于传输Web页面和其他资源的协议。 下面详细介绍一下HTTP的各个版本: 1.HTTP/0.9 这是最早的HTTP版本,于1991年发布。它非常简单,只能传输HTML格式的文本,并且不支持其他类型的资源、请求头和状态码。 2.HTTP/1…...
玩转ChatGPT:Custom instructions (vol. 1)
一、写在前面 据说GPT-4又被削了,前几天让TA改代码,来来回回好几次才成功。 可以看到之前3小时25条的限制,现在改成了3小时50条,可不可以理解为:以前一个指令能完成的任务,现在得两条指令? 可…...

黄东旭:The Future of Database,掀开 TiDB Serverless 的引擎盖
在 PingCAP 用户峰会 2023 上, PingCAP 联合创始人兼 CTO 黄东旭 分享了“The Future of Database”为主题的演讲, 介绍了 TiDB Serverless 作为未来一代数据库的核心设计理念。黄东旭 通过分享个人经历和示例,强调了数据库的服务化而非服务化…...

Linux环境搭建(XShell+云服务器)
好久不见啊,放假也有一周左右了,简单休息了下(就是玩了几天~~),最近也是在学习Linux,现在正在初步的学习阶段,本篇将会简单的介绍一下Linux操作系统和介绍Linux环境的安装与配置,来帮…...

-bash: /bin/rm: Argument list too long
有套数据库环境,.aud文件太多导致/u01分区使用率过高,rm清理时发现报错如下 [rootdb1 audit]# rm -rf ASM1_ora_*202*.aud -bash: /bin/rm: Argument list too long [rootdb1 audit]# rm -rf ASM1_ora_*20200*.aud -bash: /bin/rm: Argument list too…...

5个步骤完成Linux 搭建Jdk1.8环境
1:首先,在Linux系统中创建一个目录,用于存放JDK文件。可以选择在/opt目录下创建一个新的文件夹,例如/opt/jdk。 sudo mkdir /opt/jdk 2:将下载的jdk-8u381-linux-x64.tar.gz文件复制到新创建的目录中。 sudo cp jdk…...

【JAVASE】运算符
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈Java 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 运算符 1. 什么是运算符2. 算术运算符3.…...

Emacs之改造搜索文件fd-dired(基于fd命令)(一百二十一)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

字典序排数(力扣)思维 JAVA
给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。 示例 1: 输入:n 13 输出:[1,10,11,12,13,2,3,4,5,6,7,8,9] 示例 2: 输入:n 2 输…...

NLP 中的pad/padding操作代码分析
今天分析一下NLP中的pad操作代码: 该方法的作用是将输入的序列列表seqs进行填充操作,使其具有相同的长度,以便进行批处理。填充使用指定的pad_token进行,并生成一个对应的mask标志列表,用于标记哪些部分是填充内容&am…...

JavaWeb 速通HTTP
目录 一、HTTP快速入门 1.HTTP简介 : 2.HTTP请求头 : 3.HTTP响应头 : 二、HTTP响应状态码 1.基本介绍 : 2.常见状态码 : 3.状态码的分类 : 4.完整状态码汇总 : 三、HTTP请求包和响应包 1.请求包分析 : 1 GET请求 (1) 说明 (2) doGet返回数据给浏览器 (3) form表单提…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
