KMP算法总结
KMP算法总结
- BF算法引导
- BF算法步骤(图片演示)
- 代码演示
- KMP算法
- 推next数组
- 代码演示
BF算法引导
BF算法是一个暴力的字符串匹配算法,时间复杂度是o(m*n)
假设主串和子串分别为
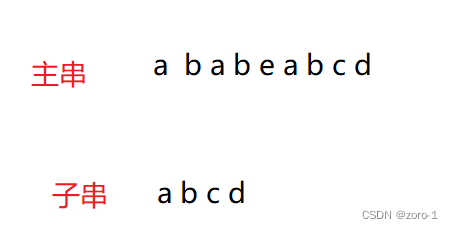
我们想要找到子串在主串的位置
BF算法核心:BF算法就是同时遍历子串和主串,如果不相同就将子串指针回退到首位,主串指针回退到这次遍历的起点的下一个位置
我们指定主串的指针为i,子串的指针为j,如下图:
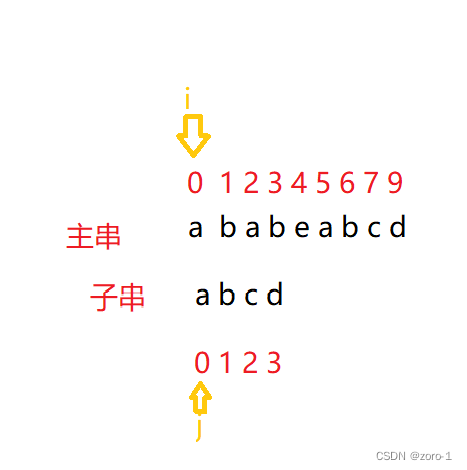
BF算法步骤(图片演示)
匹配的过程,我将用图来阐释:
1.第一趟
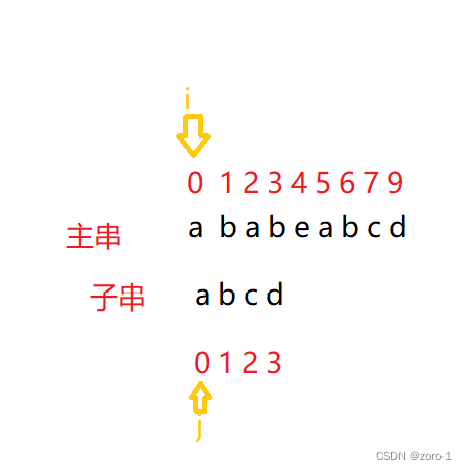
i++;
j++;
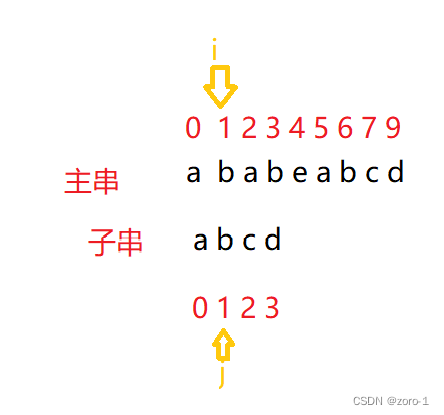
i++;
j++;
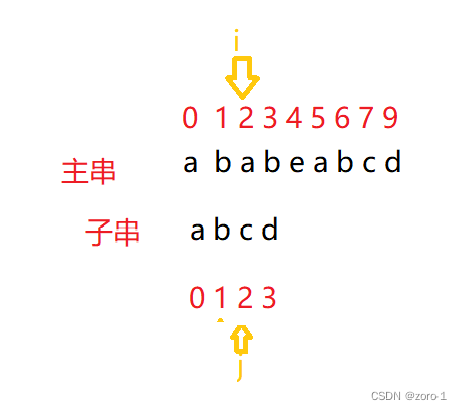
这时我们发现,i和j指向的内容不一样了
这时我们进入下一趟
2.第二趟
i=i-j+1;
(这里就是主串指针回退到这次遍历的起点的下一个位置,因为每次都是i和j同时走,但j每次都是从0开始走,j同时记录了i每次走了多少步,i-j就是回退到这一趟的起点,但这个起点我们试过了,就是+1,从下一个位置开始试)
j=0;
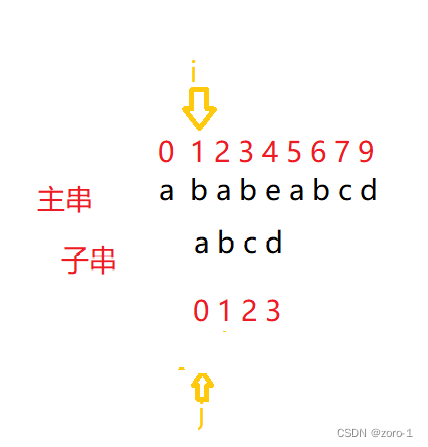
这里我们发现,i和j指向的内容不一样了
这时我们进入下一趟
3.第三趟
i=i-j+1;
j=0;
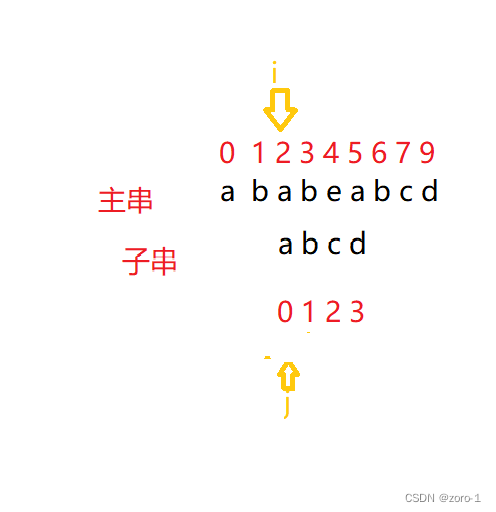
i++;
j++;
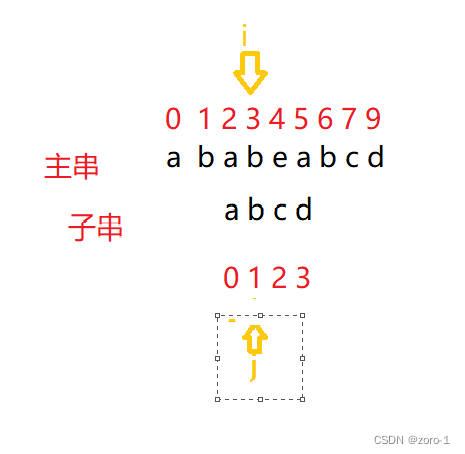
i++;
j++;
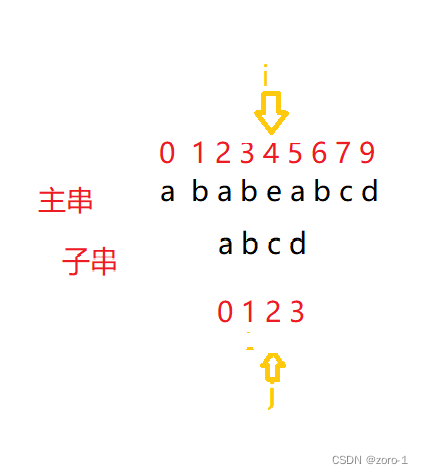
这里我们发现,i和j指向的内容不一样了
这时我们进入下一趟
4.第四趟
i=i-j+1;
j=0;
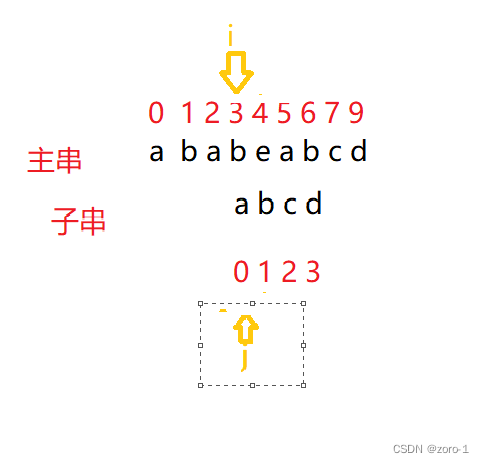
这里我们发现,i和j指向的内容不一样了
这时我们进入下一趟
5.第五趟
i=i-j+1;
j=0;

这里我们发现,i和j指向的内容不一样了
这时我们进入下一趟
6.第六趟
i=i-j+1;
j=0;
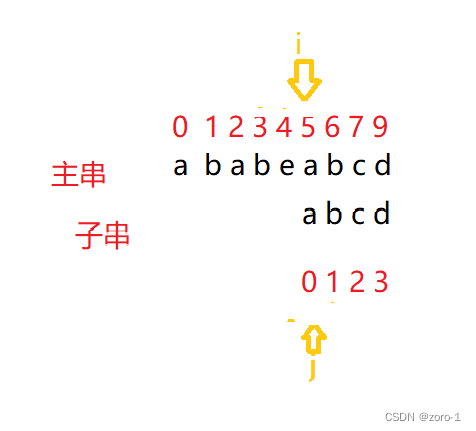
i++;
j++;
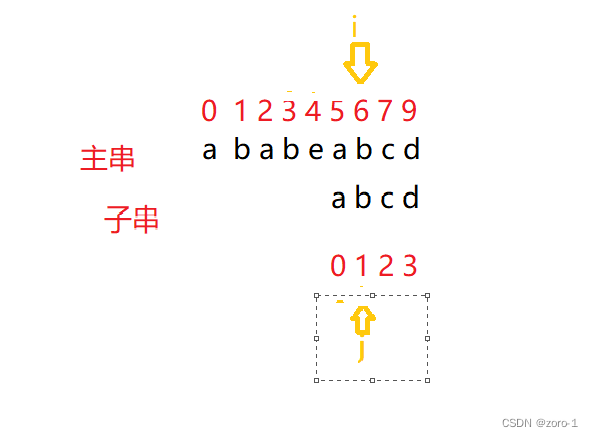
i++;
j++;
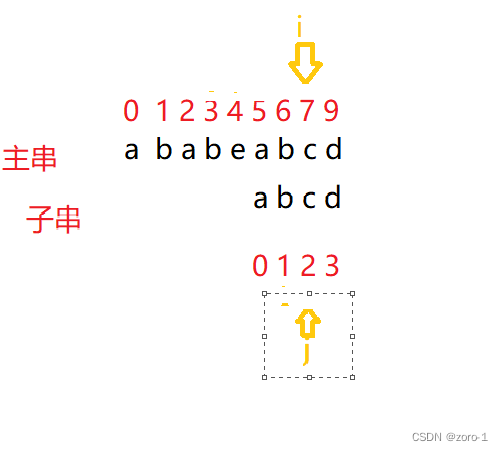
i++;
j++;
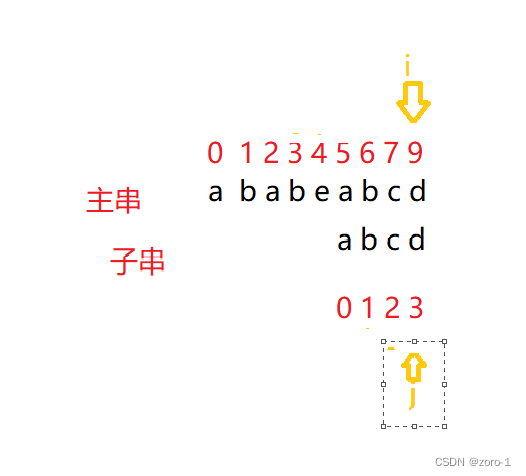
i++;
j++;

这时我们发现主串和子串都遍历结束(这个例子有点奇怪,一般只有一个遍历结束,整个程序就能判断是否有子串,并找到子串位置)
我们不难发现只有当子串遍历完,才能说明主串有这个子串
代码演示
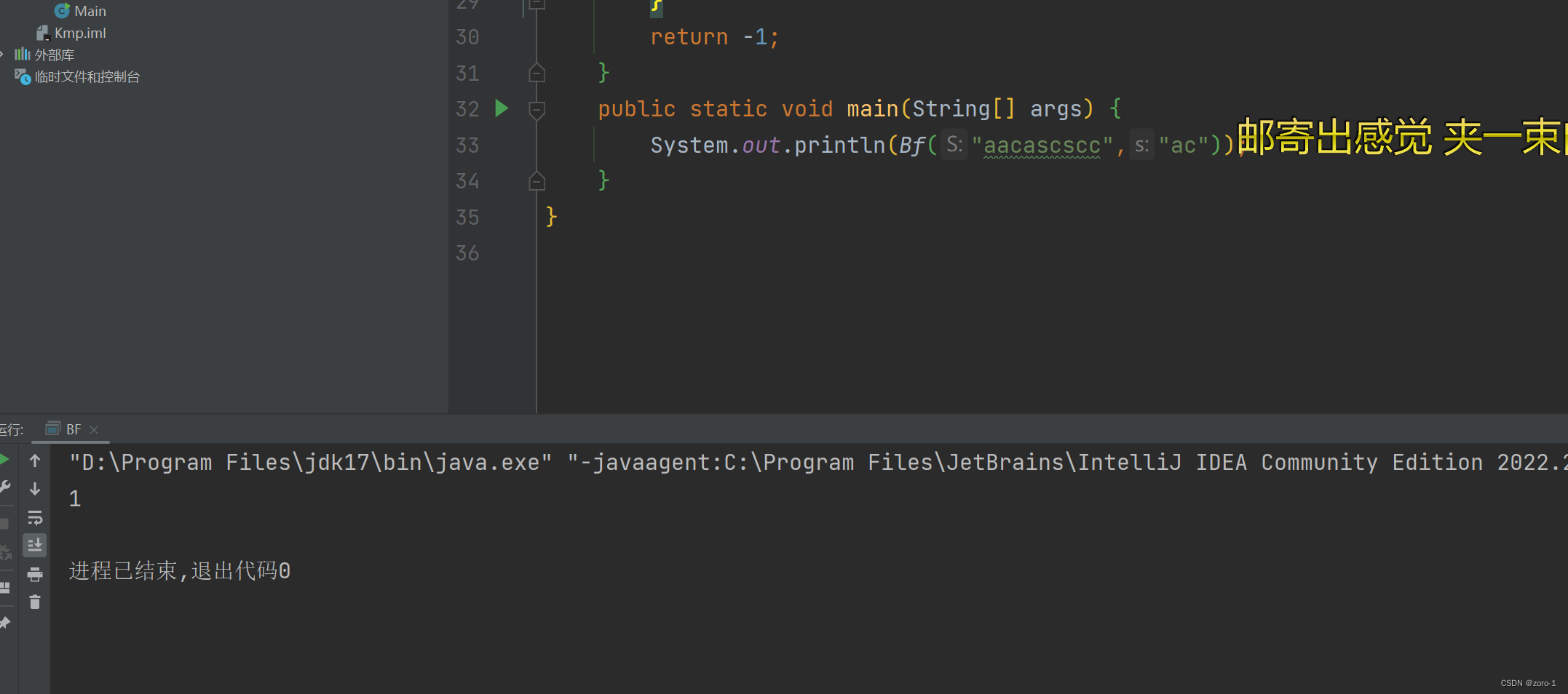
public class BF {static int Bf(String S,String s){//空字符串if(S==null||s==null){return -1;}//主串长度int SUM=S.length();//子串长度int sum=s.length();//字符串长度为0if(SUM==0||sum==0){return -1;}//指针int i=0;int j=0;while (i<SUM&&j<sum){if(S.charAt(i)==s.charAt(j)){i++;j++;}else {i=i-j+1;j=0;}}if(j>=sum){return i-j;}return -1;}public static void main(String[] args) {System.out.println(Bf("aacascscc","ac"));}
}
KMP算法
KMP也是一种字符串匹配算法,只不过他利用了遍历过的串的信息,减少了趟数,最重要就是理解他怎么利用信息
举个例子

我们指定主串的指针为i,子串的指针为j,如下图:
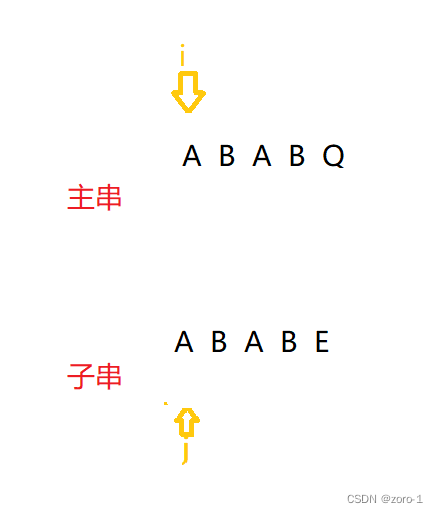
i++;
j++;
一直到匹配不正确的地方
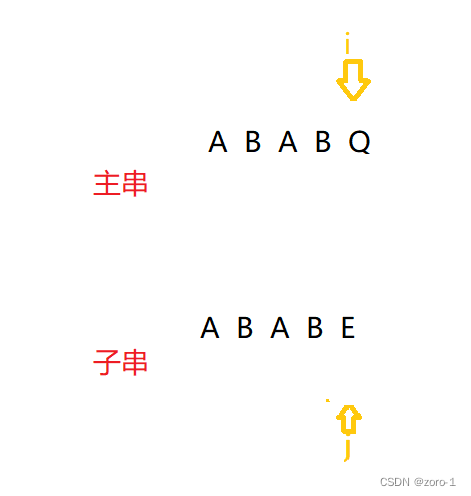
我们想让I指针停下来,只移动j指针,(这是我们想的就是这时i要回退,我们不想让他回退,但又不能丢下前面的,所以我们看前面还有什么能用上的)这时,我们遍历了主串的ABAB ,和子串的ABAB,他们两个肯定是相同的因为刚刚遍历了,如果不相同肯定会停下来,如果是BF算法我们肯定会i=i-j+1;j++;但现在我们想利用我们遍历过的ABAB的信息,我的方法是向后拖拽子串,只要发生拖拽,主串的开头A和子串结尾的B肯定是用不上了,我们必须求的是主串的(从后面开始,如果是从BAB开始算前缀即使前面匹配后面不匹配也没有用)后缀和子串的(从前面开始)前缀,(这里就是为什么求主串的后缀和子串的前缀)
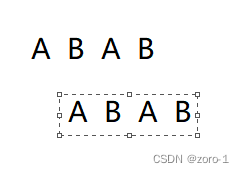
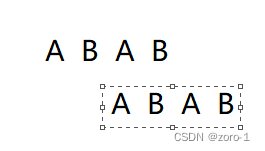
拖拽两次,我们发现主串和子串有AB重叠,这时我们就能继续遍历了(我的思考是这里我们利用了ABAB重叠的信息,省去了i指针回退到主串的下标为2,子串下标为0的地方一点点++匹配,而主串前面AB我们发现没有匹配,所以就丢弃)
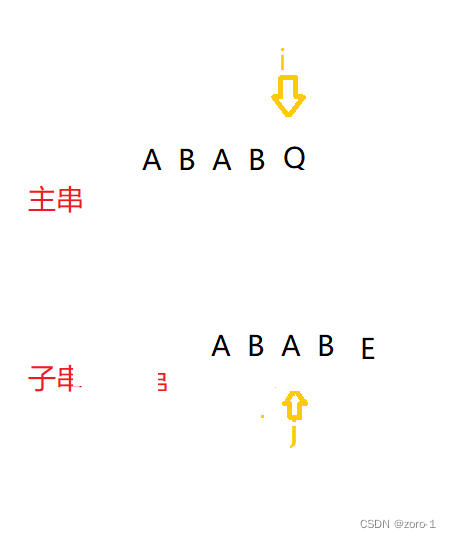
现在我们想知道怎么利用匹配过的信息,怎么一下就能找到拖拽后j到的位置
就要引入next数组,来存储j指针在每个位置匹配失败要回退到哪
推next数组
假设有这样一个字符串

规则如下:

前两个下标为0,1的就是固定的,
从下标为2开始,假设匹配失败了,ab内找以a开头以b结尾,除了本身没有这样的字符串,回退到0,
下标为3时,假设匹配失败了,aba内找以a开头以a结尾,有这样的字符串,回退到1,
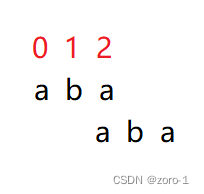
下标为3时,假设匹配失败了,abab内找以a开头以b结尾,有这样的字符串,回退到2,
后面的自行计算,结果为

给个例题,请求出他的next数组:

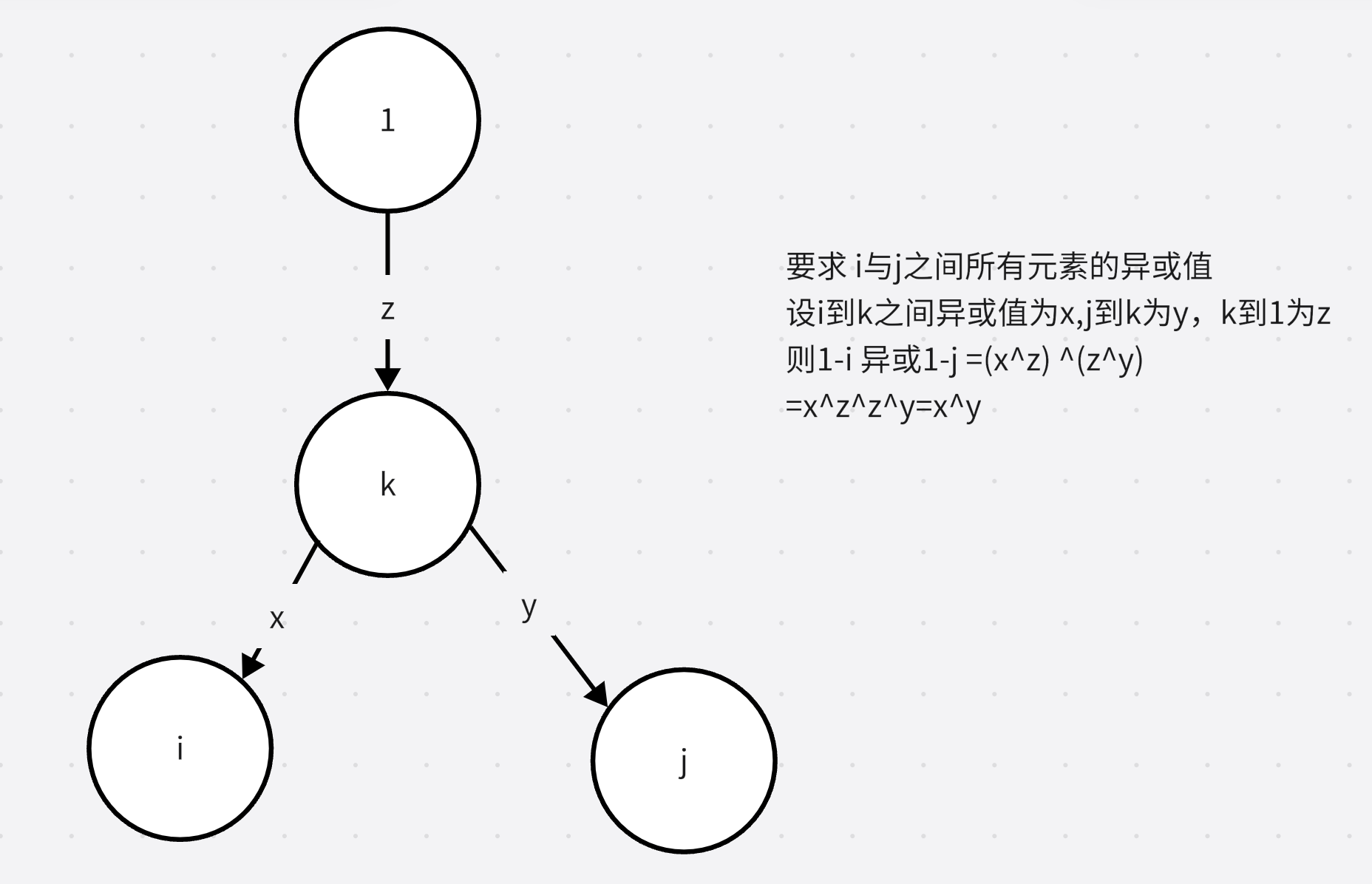
接下来我们进行一个推理
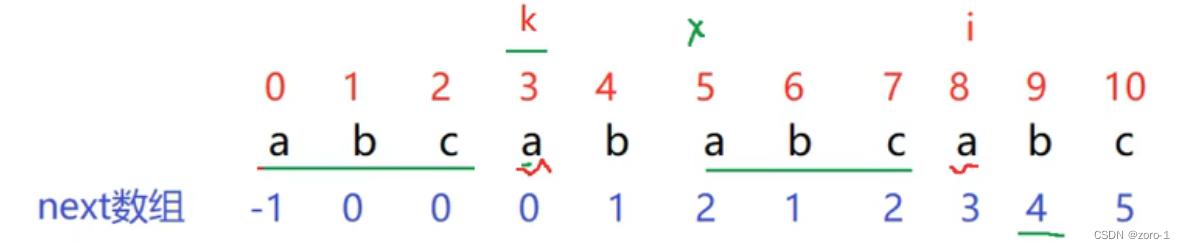
设原字符数组为p【】
如上图所示,next【i】=k,假设p【i】==p【k】如上图所示,那么
p【0】…p【k-1】==p【x】…p【i-1】
又已知k-0i-x得到xi-k
p【0】…p【k-1】==p【i-k】…p【i-1】
又因为p【i】==p【k】所以p【0】…p【k】==p【i-k】…p【i】
所以next【i+1】==k+1
推出来的意思是p【8】这个前面有abc和前面的abc匹配p【3】和p【8】又相等那么p【9】找前面的匹配时直接p【8】前面找到的abc加p【8】;
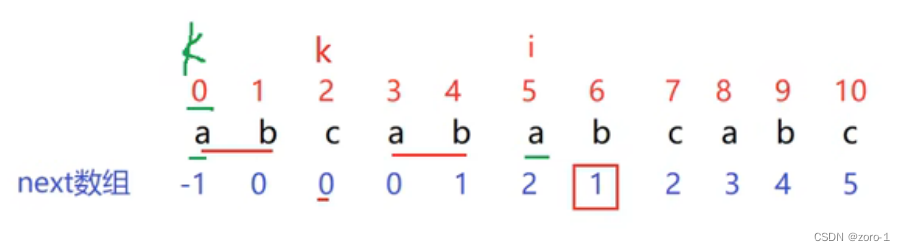
如上图所示,next【i】=k,假设p【i】!=p【k】如上图所示,那么
不是我们要找的,我们就再回退到k=0这时p【i】==p【k】
这时我们又能用next【i+1】==k+1,next【6】=k+1=1
代码演示
public class KMP {public static void main(String[] args) {System.out.println(KMP("CSA","SA"));}public static int KMP (String s, String sub){int lens = s.length(), lensub = sub.length();int[] next = new int[lensub];//next数组 存放匹配不上的子串要跳跃的下标getNext(next, sub);int i = 0, j = 0;// i 遍历主串, j 遍历子串while (i < lens && j < lensub) {if (j == -1 || s.charAt(i) == sub.charAt(j)) {i++;j++;//逐一比较,相同的看下一个//当子串的第一个字符就与主串的字符不相等时,j++为0,i向后移动一位} else {j = next[j];}}if (j == lensub) {return i - j;//上面while循环结束条件是因为 遍历发现子串所有均与主串相等} else {return -1;}}public static void getNext ( int[] next, String sub){next[0] = -1;next[1] = 0;//固定int i = 2;//i表示当前所求next数组的下标int k = 0;//比较是否相等的前一项while (i < sub.length()) {if (k == -1 || sub.charAt(i - 1) == sub.charAt(k)) {//就是一直回退直到就是说没有利用的重叠部分就是k=-1next[i] = k + 1;//当k==-1时,证明【0】与【j-1】里无相等字符,k++为0,i移向下一位k++;i++;} else {k = next[k];}}}}之后如果有新的想法会及时补充,大家如果有不同见解欢迎评论区留言

相关文章:

KMP算法总结
KMP算法总结 BF算法引导BF算法步骤(图片演示)代码演示 KMP算法推next数组代码演示 BF算法引导 BF算法是一个暴力的字符串匹配算法,时间复杂度是o(m*n) 假设主串和子串分别为 我们想要找到子串在主串的位置 BF算法核…...

消息中间件ActiveMQ介绍
一、消息中间件的介绍 介绍 消息队列 是指利用 高效可靠 的 消息传递机制 进行与平台无关的 数据交流,并基于 数据通信 来进行分布式系统的集成。 特点(作用) 应用解耦 异步通信 流量削峰 (海量)日志处理 消息通讯 …... 应用场景 根据消息队列的特点&a…...

【100天精通python】Day9:数据结构_字典、集合
目录 目录 1 字典 1.1 字典的基本操作示例 1.2 字典推导式 2 集合 2.1 集合的常用操作示例 3 列表、元组、字典、集合的区别 1 字典 在Python中,字典(Dictionary)是一种无序的数据结构,用于存储键值对的集合。每个…...

上海VR全景展示,快速了解VR全景拍摄
导语: 随着科技的不断进步,虚拟现实技术的应用日益广泛。在这其中,VR全景图片作为一种数字化助力的全景拍摄方式,正逐渐成为人们关注的焦点。通过数字化技术,VR全景图片能够以360度全方位的视角呈现真实的场景&#x…...
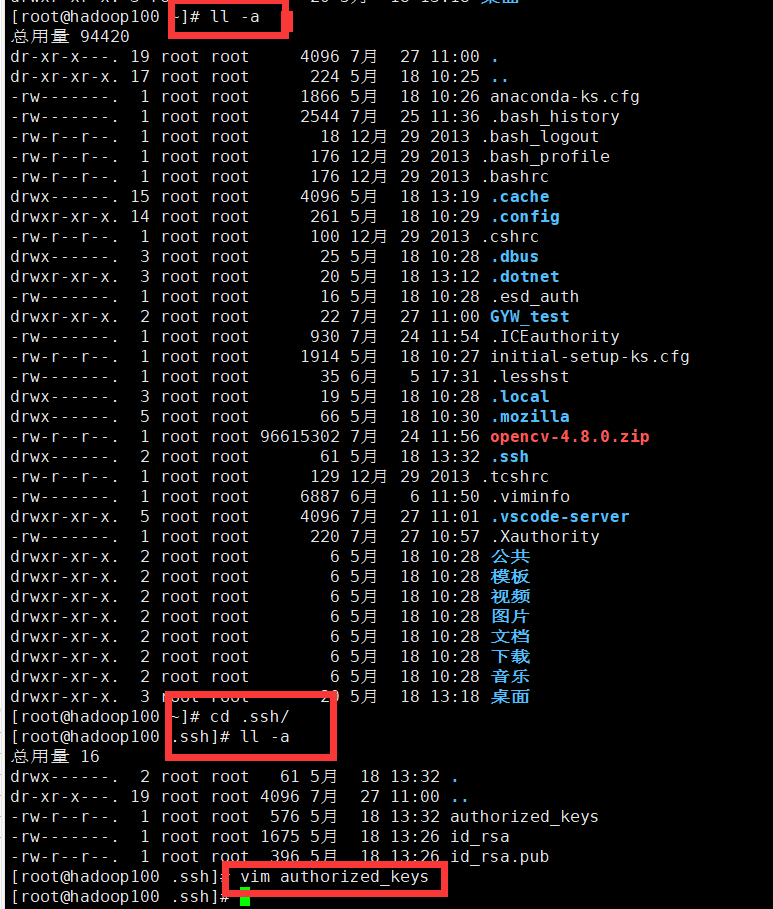
VScode远程不用再输入密码操作
安装插件remote development 1.先检查自己电脑上有没有生成一对公钥和私钥。(一般会在这个目录) 如果没有的话就自己生成一下。 打开命令行输入以下命令 ssh-keygen -t rsa2.在虚拟机中先看一下有没有公钥和私钥。如果没有的话就自己生成一下。 打开…...

MyBatis基本用法-@TableId
TableId 注解是 MyBatis Plus 框架中用于标识实体类中的主键字段的注解,它有一些可选的配置项。下面是详细说明: 首先,需要在项目中添加 MyBatis Plus 的依赖。可以在项目的 pom.xml 文件中添加以下代码: <dependency><…...

React AntDesign写一个导出数据的提示语 上面有跳转的路径,或者点击知道了,关闭该弹层
效果如下: 代码如下: ForwardDataCenterModal(_blank);export const ForwardDataCenterModal (target?: string) > {let contentBefore React.createElement(span, null, 数据正在处理中,请稍后前往);let contentAfter React.creat…...

小红书课程发光社群知识库,点亮哥专为超级个体设计解决方案
小红书课程点亮哥知识库 开创了学习小红书教育培训先河 针对超级个体轻创业的学习需求场景 创新推出了“知识库全新学习方式”。 一个人如何做好小红书? 超级个体轻创业,如何做好小红书? 通过打造个人IP、或者塑造老板个人品牌,来实现互联网变现,如何做好小红书? 就像挑…...

基于SpringBoot+Vue的摄影跟拍预定管理系统设计与实现(源码+lw+部署文档等)
博主介绍: 大家好,我是一名在Java圈混迹十余年的程序员,精通Java编程语言,同时也熟练掌握微信小程序、Python和Android等技术,能够为大家提供全方位的技术支持和交流。 我擅长在JavaWeb、SSH、SSM、SpringBoot等框架…...
HCIA 第二课总结
配置网络设备的明文密钥实验组网 实验拓扑 将一个路由器使用配置口进行连接 sys #进入系统视图模式 sysname RTA #给设备命名 user-interface console 0 #进入用户接口配置界面 authentication-mode password #配置认证模式为密钥认证 set authentication password ciphe…...

linux-------联网下载文件和配置
1.Wget Wget是一个十分常用命令行下载工具,多数Linux发行版本都默认包含这个工具。如果没有安装可在http://www.gnu.org/software/wget/wget.html下载最新版本,并使用如下命令编译安装: 1.#tar zxvf wget-1.9.1.tar.gz #cd wget-1.9.1 #./c…...
字典树Trie
Trie树又称字典树,前缀树。是一种可以高效查询前缀字符串的树,典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。 它的优点是:利用字符串…...

算法之桶排序算法
桶排序的基本思想是: 把数组 arr 划分为 n 个大小相同子区间(桶),每个子区间各自排序,最 后合并 。计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况。 1.找出待排序数组中的…...
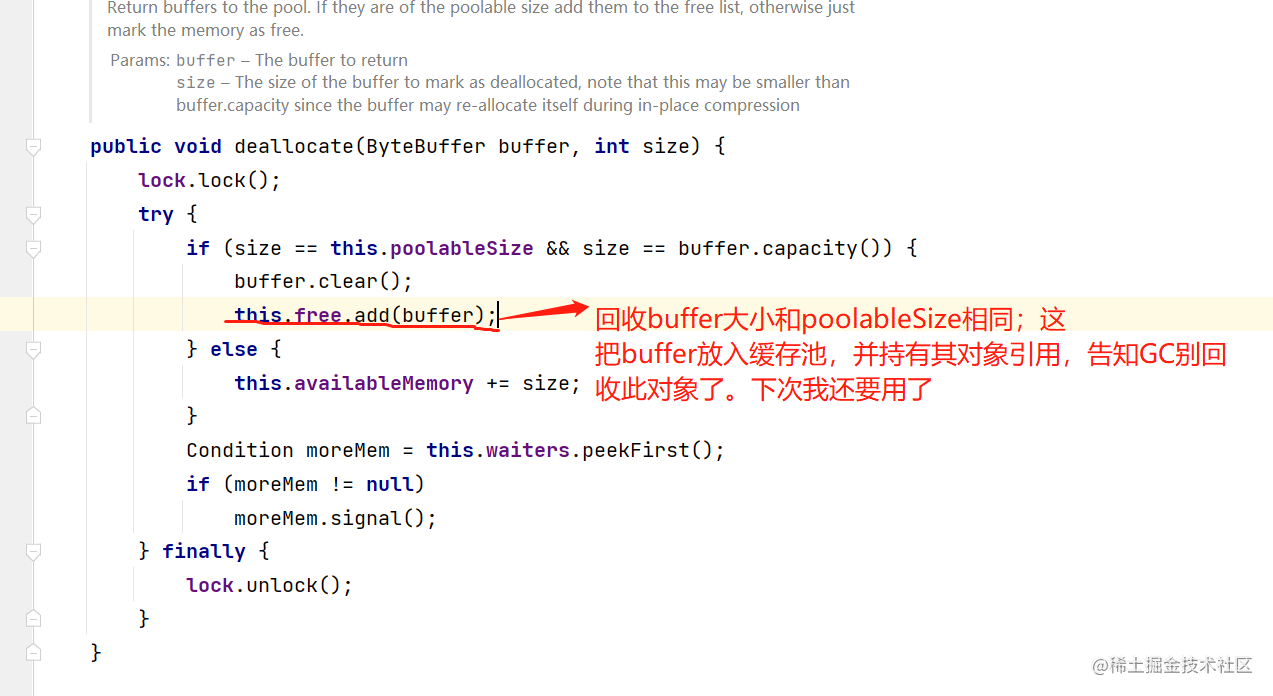
读kafka生产端源码,窥kafka设计之道(下)
背景 在上一篇文章《读kafka生产端源码,窥kafka设计之道(上)》 留下了kafka设计上比较优秀的一个点;内存的循环使用。本篇文章准备盘盘它。 好奇 为什么 kafka减少发送消息时向JVM频繁申请内存,就可以降低JVM GC的执…...
Pytorch个人学习记录总结 06
目录 神经网络-卷积层 torch.nn.Conv2d 神经网络-最大池化的使用 torch.nn.MaxPool2d 神经网络-卷积层 torch.nn.Conv2d torch.nn.Conv2d的官方文档地址 CLASS torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue,…...
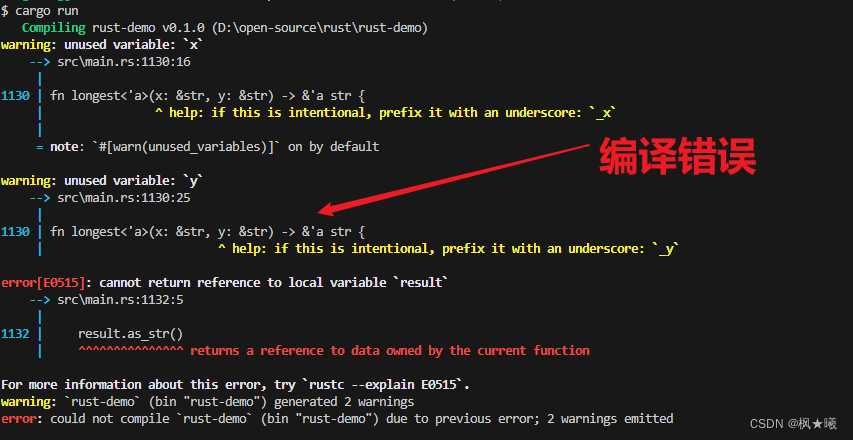
Rust之泛型、特性和生命期(四):验证有生存期的引用
开发环境 Windows 10Rust 1.71.0 VS Code 1.80.1 项目工程 这里继续沿用上次工程rust-demo 验证具有生存期的引用 生存期是我们已经在使用的另一种泛型。生存期不是确保一个类型具有我们想要的行为,而是确保引用在我们需要时有效。 我们在第4章“引用和借用”一…...
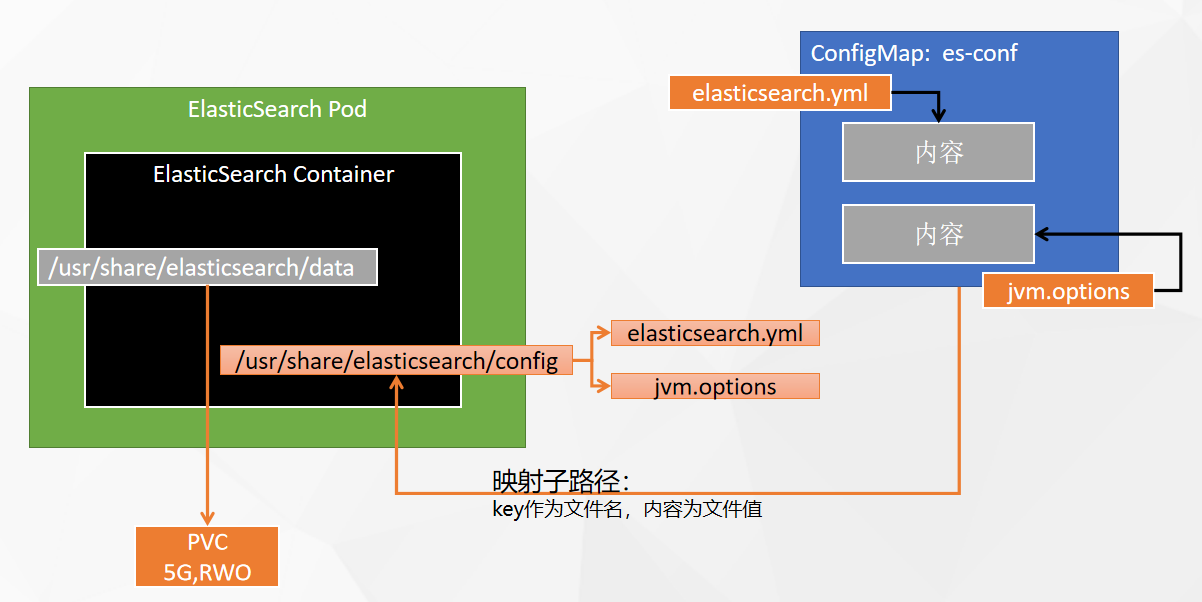
kubesphere安装中间件
kubesphere安装mysql 创建configMap [client] default-character-setutf8mb4[mysql] default-character-setutf8mb4[mysqld] init_connectSET collation_connection utf8mb4_unicode_ci init_connectSET NAMES utf8mb4 character-set-serverutf8mb4 collation-serverutf8mb4_…...
 集群模式安装)
zookeeper学习(二) 集群模式安装
前置环境 三台centos7服务器 192.168.2.201 192.168.2.202 192.168.2.150三台服务器都需要安装jdk1.8以上zookeeper安装包 安装jdk 在单机模式已经描述过,这里略过,有需要可以去看单机模式中的这部分,注意的是三台服务器都需要安装 安装…...
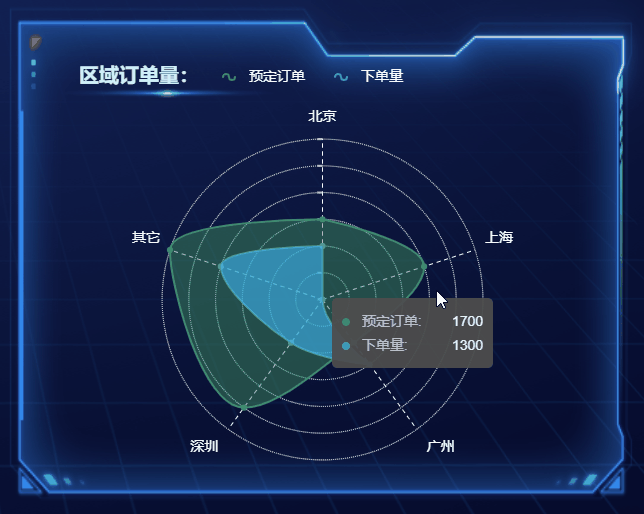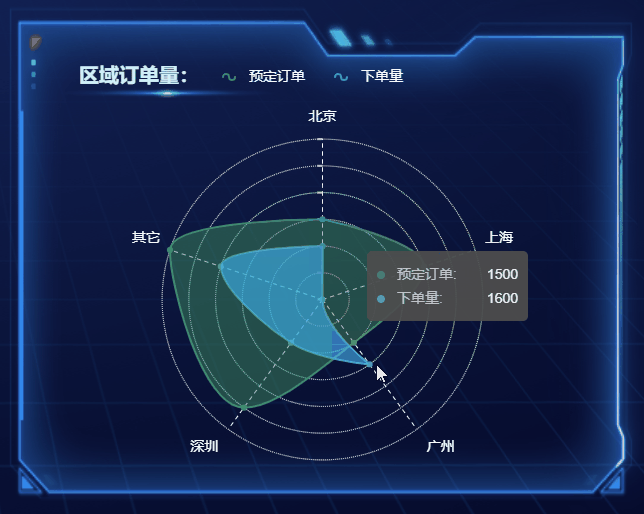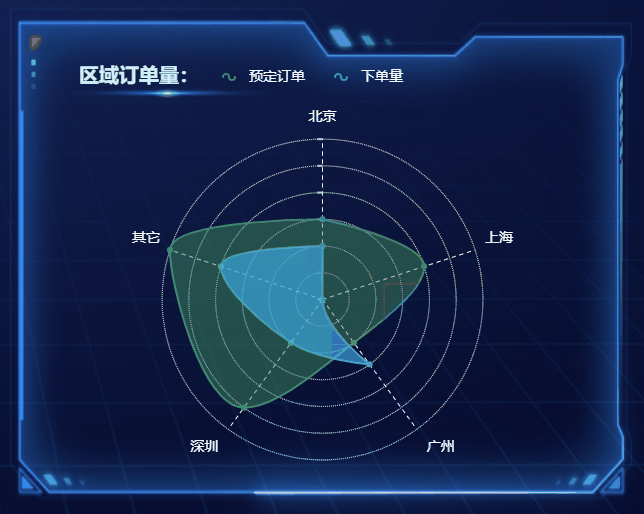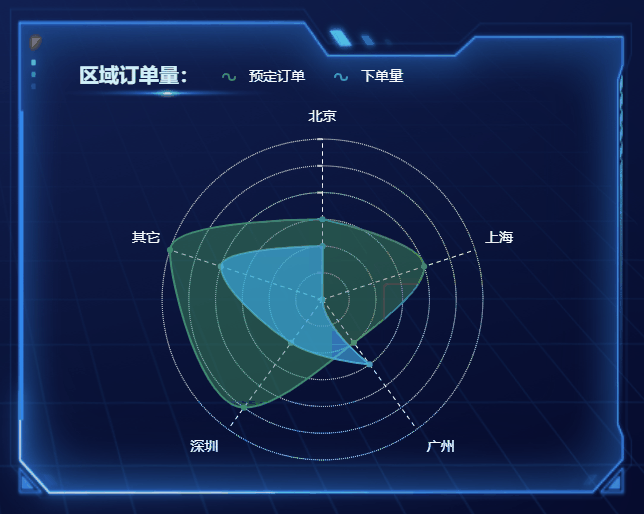
选择合适的图表,高效展现数据魅力
随着大数据时代的来临,数据的重要性愈发凸显,数据分析和可视化成为了决策和传递信息的重要手段。在数据可视化中,选择合适的图表是至关重要的一环,它能让数据更加生动、直观地呈现,为观众提供更有说服力的信息。本文将…...
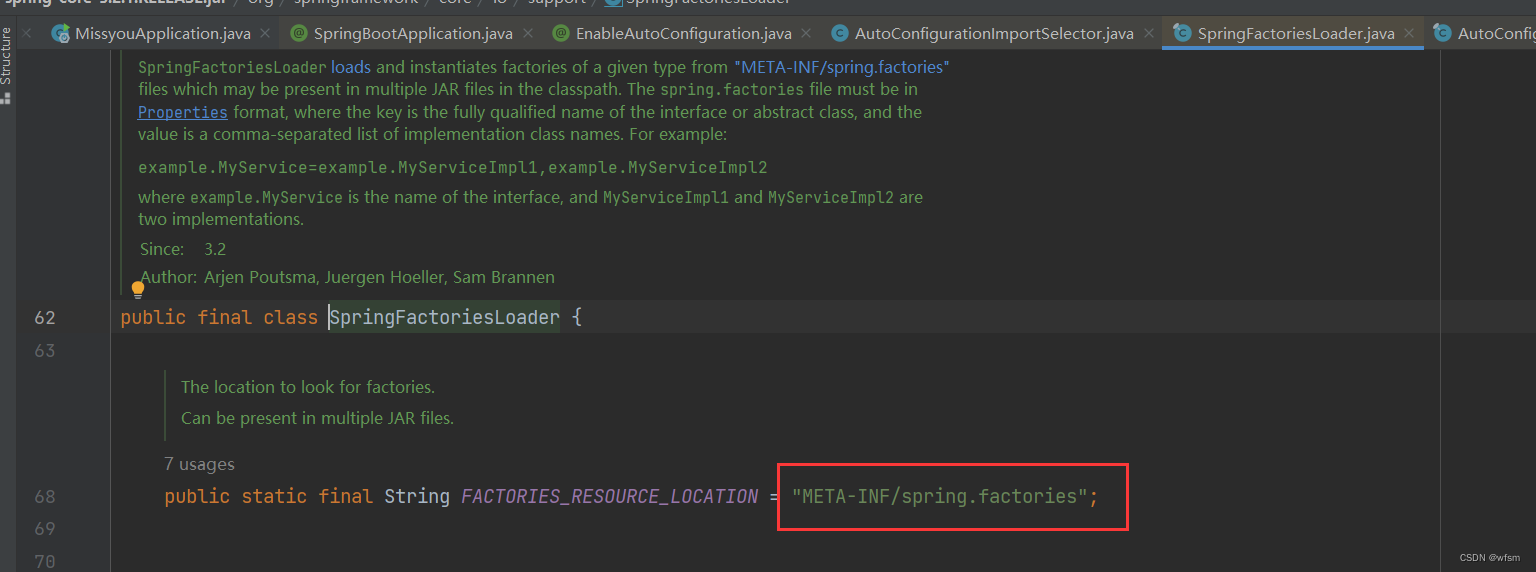
springboot自动装配
SPI spi : service provider interface : 是java的一种服务提供机制,spi 允许开发者在不修改代码的情况下,为某个接口提供实现类,来扩展应用程序 将实现类独立到配置文件中,通过配置文件控制导入ÿ…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
