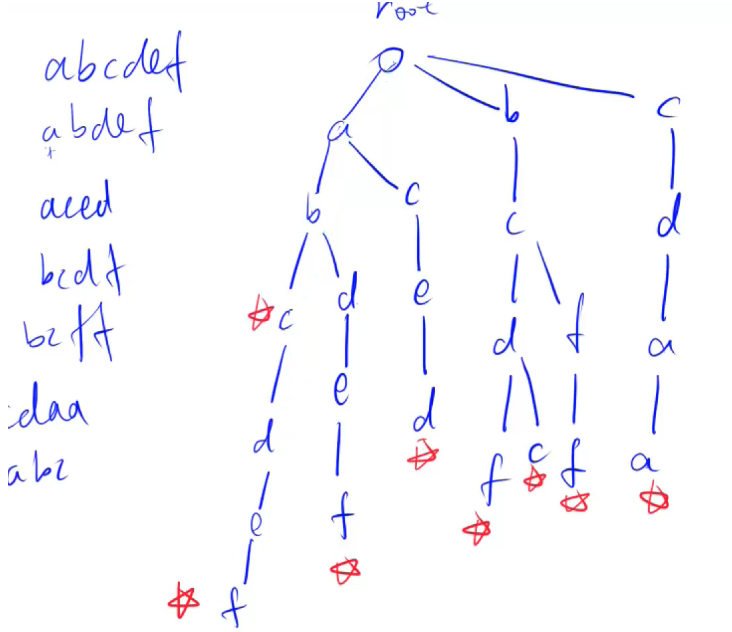
字典树Trie
Trie树又称字典树,前缀树。是一种可以高效查询前缀字符串的树,典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。`做题看到大量字符串或者大量字符就往Trie树或者哈希这边想,因为速度很快.
AcWing 835. Trie字符串统计
https://www.acwing.com/activity/content/problem/content/883/
维护一个字符串集合,支持两种操作:
I x向集合中插入一个字符串 x x x;Q x询问一个字符串在集合中出现了多少次。
共有 N N N 个操作,所有输入的字符串总长度不超过 1 0 5 10^5 105,字符串仅包含小写英文字母。
输入格式
第一行包含整数 N N N,表示操作数。
接下来 N N N 行,每行包含一个操作指令,指令为 I x 或 Q x 中的一种。
输出格式
对于每个询问指令 Q x,都要输出一个整数作为结果,表示 x x x 在集合中出现的次数。
每个结果占一行。
数据范围
1 ≤ N ≤ 2 ∗ 1 0 4 1 \le N \le 2*10^4 1≤N≤2∗104
输入样例:
5
I abc
Q abc
Q ab
I ab
Q ab
输出样例:
1
0
1
思路
Trie树模版题
代码
/*** https://www.acwing.com/problem/content/837/*/
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 1e5 + 10;
int son[N][26], cnt[N], idx;
// 下标0代表根节点和空节点,cnt用于计数,idx代表结点的索引void insert(string s) {int x = 0;for (auto c: s) {int y = c - 'a';if (!son[x][y]) son[x][y] = ++idx;// 没有该子结点就创建一个x = son[x][y]; // 走到该子节点}++cnt[x];// 标记该子节点存在的单词个数
}int query(string s) {int x = 0;for (auto c: s) {int y = c - 'a';if (!son[x][y]) return 0;// 没有该子结点就返回查询不到x = son[x][y];}return cnt[x];
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifint n;cin >> n;while (n--) {string op, s;cin >> op >> s;if (op == "I") insert(s);else cout << query(s) << endl;}return 0;
}
【模板】字典树
https://www.luogu.com.cn/problem/P8306
题目描述
给定 n n n 个模式串 s 1 , s 2 , … , s n s_1, s_2, \dots, s_n s1,s2,…,sn 和 q q q 次询问,每次询问给定一个文本串 t i t_i ti,请回答 s 1 ∼ s n s_1 \sim s_n s1∼sn 中有多少个字符串 s j s_j sj 满足 t i t_i ti 是 s j s_j sj 的前缀。
一个字符串 t t t 是 s s s 的前缀当且仅当从 s s s 的末尾删去若干个(可以为 0 个)连续的字符后与 t t t 相同。
输入的字符串大小敏感。例如,字符串 Fusu 和字符串 fusu 不同。
输入格式
本题单测试点内有多组测试数据。
输入的第一行是一个整数,表示数据组数 T T T。
对于每组数据,格式如下:
第一行是两个整数,分别表示模式串的个数 n n n 和询问的个数 q q q。
接下来 n n n 行,每行一个字符串,表示一个模式串。
接下来 q q q 行,每行一个字符串,表示一次询问。
输出格式
按照输入的顺序依次输出各测试数据的答案。
对于每次询问,输出一行一个整数表示答案。
样例 #1
样例输入 #1
3
3 3
fusufusu
fusu
anguei
fusu
anguei
kkksc
5 2
fusu
Fusu
AFakeFusu
afakefusu
fusuisnotfake
Fusu
fusu
1 1
998244353
9
样例输出 #1
2
1
0
1
2
1
提示
数据规模与约定
对于全部的测试点,保证 1 ≤ T , n , q ≤ 1 0 5 1 \leq T, n, q\leq 10^5 1≤T,n,q≤105,且输入字符串的总长度不超过 3 × 1 0 6 3 \times 10^6 3×106。输入的字符串只含大小写字母和数字,且不含空串。
说明
std 的 IO 使用的是关闭同步后的 cin/cout,本题不卡常。
思路
因为这里需要统计的是前缀,因此每走一个点,都需要将cnt数组加1
这里不仅有小写,还有大写和数字,可以把小写映射为0-26,大写映射为26-52,数字映射为36-62 ,都是左闭右开区间。
有多组测试数据,需要初始化son为0,idx为0,cnt为0
数据比较大,需要开cin和cout优化
Trie第一维开多大取决于字符串长度,与idx能增长到多少有关,尽可能开大一点5e6没问题,第二维取决于字符串里面字符的个数
代码
/*** https://www.luogu.com.cn/problem/P8306*/
#include <bits/stdc++.h>#define int long long
using namespace std;//空间怎么看开多大?看数据范围 输入总字符串总长度不超过3e6
const int N = 3e6 + 10;
int son[N][65], cnt[N], idx;int get(char c) {if (c >= 'a' && c <= 'z') return c - 'a';if (c >= 'A' && c <= 'Z') return c - 'A' + 26;if (c >= '0' && c <= '9') return c - '0' + 26 + 26;}void insert(string s) {int x = 0;for (char c: s) {int y = get(c);if (!son[x][y]) son[x][y] = ++idx;x = son[x][y];cnt[x]++;}
}int query(string s) {int x = 0;for (auto c: s) {int y = get(c);if (!son[x][y]) return 0;x = son[x][y];}return cnt[x];
}void solve() {int n, q;cin >> n >> q;string s;while (n--) { cin >> s, insert(s); }while (q--) { cin >> s, cout << query(s) << '\n'; }//清空字典树,不使用memset,使用forfor (int i = 0; i <= idx; i++) {for (int j = 0; j < 63; j++) {son[i][j] = 0;}}for (int i = 0; i <= idx; i++) cnt[i] = 0;idx = 0;
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin.tie(0), cout.tie(0), ios::sync_with_stdio(false);int t;cin >> t;while (t--) solve();return 0;
}
AcWing 143. 最大异或对
在给定的 N N N 个整数 A 1 , A 2 … … A N A_1,A_2……A_N A1,A2……AN 中选出两个进行 x o r xor xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数 N N N。
第二行输入 N N N 个整数 A 1 A_1 A1~ A N A_N AN。
输出格式
输出一个整数表示答案。
数据范围
1 ≤ N ≤ 1 0 5 1 \le N \le 10^5 1≤N≤105,
0 ≤ A i < 2 31 0 \le A_i < 2^{31} 0≤Ai<231
输入样例:
3
1 2 3
输出样例:
3
思路
先将所有数插入到01Trie树中,然后遍历一遍数组,去找可以使得和他异或起来最大的数,时间复杂度是 n l o g n nlogn nlogn的,因为树每层最多30个.
如何找异或起来最大:
比如当前节点为0,那就看!0的节点是否存在,如果存在,走过去一定是最优的,因为在这一位异或起来的结果就可以变成1了,否则只能往0走。
代码
/*** https://www.acwing.com/problem/content/145/*/
#include <bits/stdc++.h>#define int long long
using namespace std;const int N = 1e5 + 10;
int son[N * 32][2], idx;void insert(int t) {int x = 0;for (int i = 30; i >= 0; i--) {int y = t >> i & 1;if (!son[x][y]) son[x][y] = ++idx;x = son[x][y];}
}int query(int t) {int x = 0, res = 0;for (int i = 30; i >= 0; i--) {int y = t >> i & 1;if (son[x][!y]) {//另一个存在res = res * 2 + !y;x = son[x][!y];} else {res = res * 2 + y;x = son[x][y];}}return res;
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifint n;cin >> n;vector<int> a(n);for (int i = 0; i < n; ++i)cin >> a[i];for (int i = 0; i < n; ++i) insert(a[i]);int mx = 0;for (int i = 0; i < n; ++i) mx = max(mx, a[i] ^ query(a[i]));cout << mx << endl;return 0;
}
最长异或路径
题目描述
给定一棵 n n n 个点的带权树,结点下标从 1 1 1 开始到 n n n。寻找树中找两个结点,求最长的异或路径。
异或路径指的是指两个结点之间唯一路径上的所有边权的异或。
输入格式
第一行一个整数 n n n,表示点数。
接下来 n − 1 n-1 n−1 行,给出 u , v , w u,v,w u,v,w ,分别表示树上的 u u u 点和 v v v 点有连边,边的权值是 w w w。
输出格式
一行,一个整数表示答案。
样例 #1
样例输入 #1
4
1 2 3
2 3 4
2 4 6
样例输出 #1
7
提示
最长异或序列是 1 , 2 , 3 1,2,3 1,2,3,答案是 7 = 3 ⊕ 4 7=3\oplus 4 7=3⊕4。
数据范围
1 ≤ n ≤ 100000 ; 0 < u , v ≤ n ; 0 ≤ w < 2 31 1\le n \le 100000;0 < u,v \le n;0 \le w < 2^{31} 1≤n≤100000;0<u,v≤n;0≤w<231。
思路
要求两个点之间的所有元素的异或值,设为 i , j i,j i,j两点, 可以变成 i i i到根节点异或 j j j到根节点的异或值。
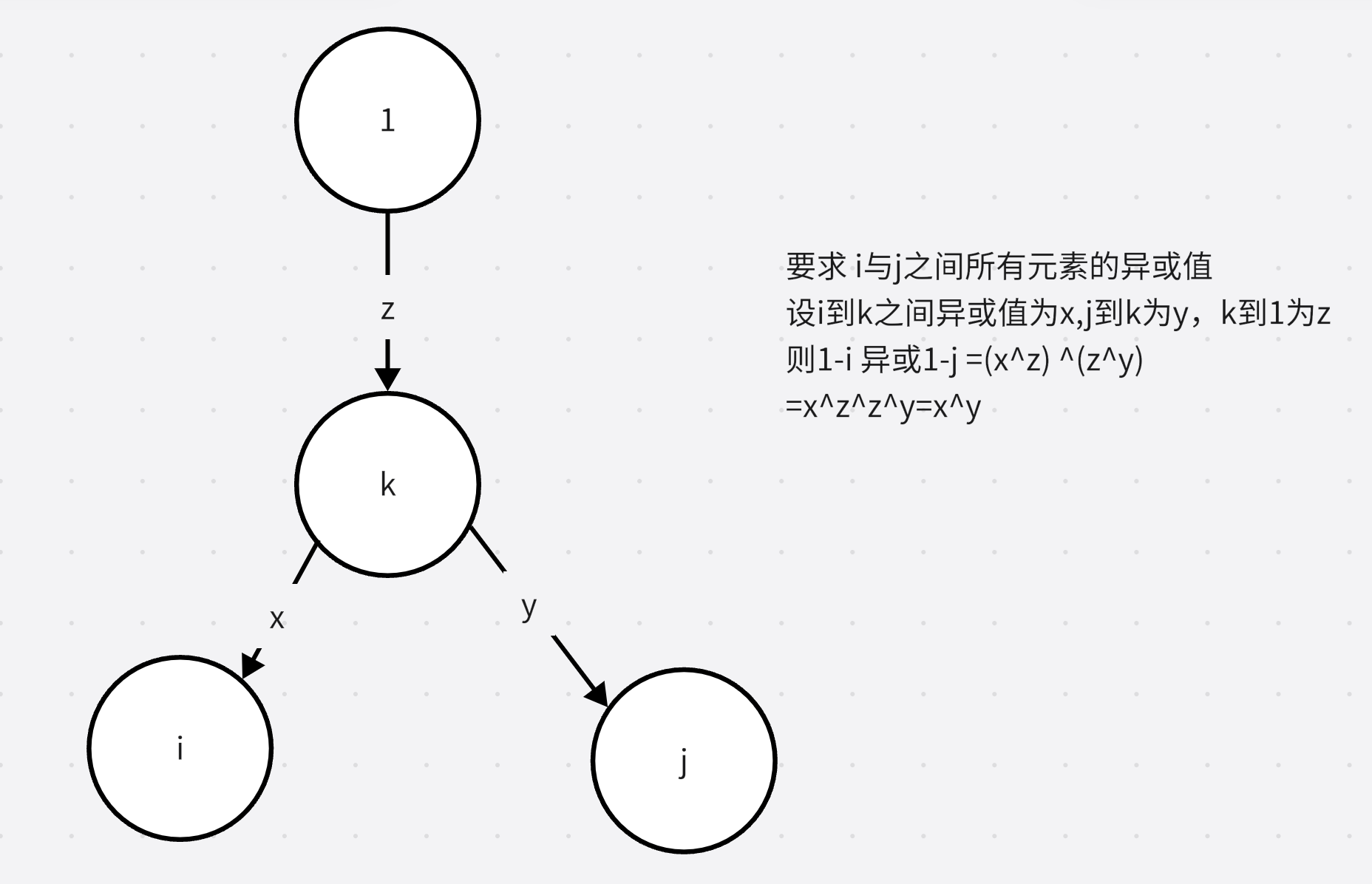
因此我们可以去求每个点到根节点1的异或值,使用dfs即可,记录在sum中
然后遍历每个点,求当前点到根节点亦或值sum[i]可以异或得到的最大值。
之后就和上面一题一样了
代码
#include <bits/stdc++.h>using namespace std;typedef struct edge {int to, w;
} edge;const int N = 1e5 + 10;
int son[N * 31][2], cnt[N], idx;
int sum[N];// 存到根节点到异或值
vector<edge> e[N];
int n;void dfs(int x, int fa) {for (auto [y, w]: e[x]) {if (y == fa) continue;sum[y] = sum[x] ^ w;dfs(y, x);}
}void insert(int t) {int x = 0;for (int i = 30; i >= 0; i--) {int y = t >> i & 1;if (!son[x][y]) son[x][y] = ++idx;x = son[x][y];}
}int query(int t) {int x = 0, res = 0;for (int i = 30; i >= 0; i--) {int y = t >> i & 1;if (son[x][!y]) {res += 1 << i;x = son[x][!y];} else {x = son[x][y];}}return res;
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;for (int i = 1; i <= n - 1; i++) {int x, y, w;cin >> x >> y >> w;e[x].push_back({y, w});e[y].push_back({x, w});}dfs(1, 0);for (int i = 1; i <= n; i++) insert(sum[i]);int res = 0;for (int i = 1; i <= n; i++) res = max(res, query(sum[i]));cout << res << endl;return 0;
}
最小异或对
题目描述
https://ac.nowcoder.com/acm/contest/53485/F
给出一个多重集合(元素可以重复的集合),你需要提供以下操作:
- ADD x,向多重集合里添加一个元素x,多重集合内元素可以重复
- **DEL x,**从多重集合中删除一个元素x,保证要删除的元素一定存在,如果存在多个x则仅删除其中任意1个
- QUE,查询集合中的最小异或对的值,即找到集合中任何**两个元素(可以相等)**异或能得到的最小值,保证询问时集合包含的元素数量不少于2个
对于每个QUE操作,你需要输出查询的结果.
以上操作中涉及的操作数x均为非负整数.
1 < = n < = 2 ∗ 1 0 5 , 0 < = x < 2 30 1<=n<=2*10^5 ,0<=x<2^{30} 1<=n<=2∗105,0<=x<230
思路-01Trie
与最大异或对类似
思路-结论
最小异或对的结论:最小异或对一定为数组排序后相邻两个数的异或值
证明:
设 a < b < c a<b<c a<b<c,我们现在需要证明最小异或对只可能是ab或者bc
设c与a的第一个不同的位为第x位(从高向低看),则x位上面c一定为1,a一定为0 ,b可以为0或者1
a,b,c在x位置之前的数字都是相同的。
因此在x位上面,ac的这一位一定为1,ab和b^c一定会有一个异或起来在这一位为0,
因此a^c不可能是最小的,也就是一定是相邻两个数异或起来才是最小。
可以使用平衡树进行增删改查操作.
代码
#include <bits/stdc++.h>#define int long long
using namespace std;multiset<int> s, res;
int n, x;
string op;void add() {auto it = s.lower_bound(x);if (it != s.end()) res.insert(x ^ *it);if (it != s.begin()) res.insert(x ^ *prev(it));if (it != s.end() && it != s.begin()) res.erase(res.lower_bound(*it ^ *prev(it)));s.insert(x);
}void del() {s.erase(s.find(x));auto it = s.lower_bound(x);if (it != s.end()) res.erase(res.find(x ^ *it));if (it != s.begin()) res.erase(res.find(x ^ *prev(it)));if (it != s.end() && it != s.begin()) res.insert(*it ^ *prev(it));
}int que() {return *res.begin();
}signed main() {
#ifndef ONLINE_JUDGEfreopen("test.in", "r", stdin);freopen("test.out", "w", stdout);
#endifcin >> n;while (n--) {cin >> op;if (op == "ADD") {cin >> x;add();} else if (op == "DEL") {cin >> x;del();} else cout << que() << endl;}return 0;
}
相关文章:

字典树Trie
Trie树又称字典树,前缀树。是一种可以高效查询前缀字符串的树,典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。 它的优点是:利用字符串…...

算法之桶排序算法
桶排序的基本思想是: 把数组 arr 划分为 n 个大小相同子区间(桶),每个子区间各自排序,最 后合并 。计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况。 1.找出待排序数组中的…...
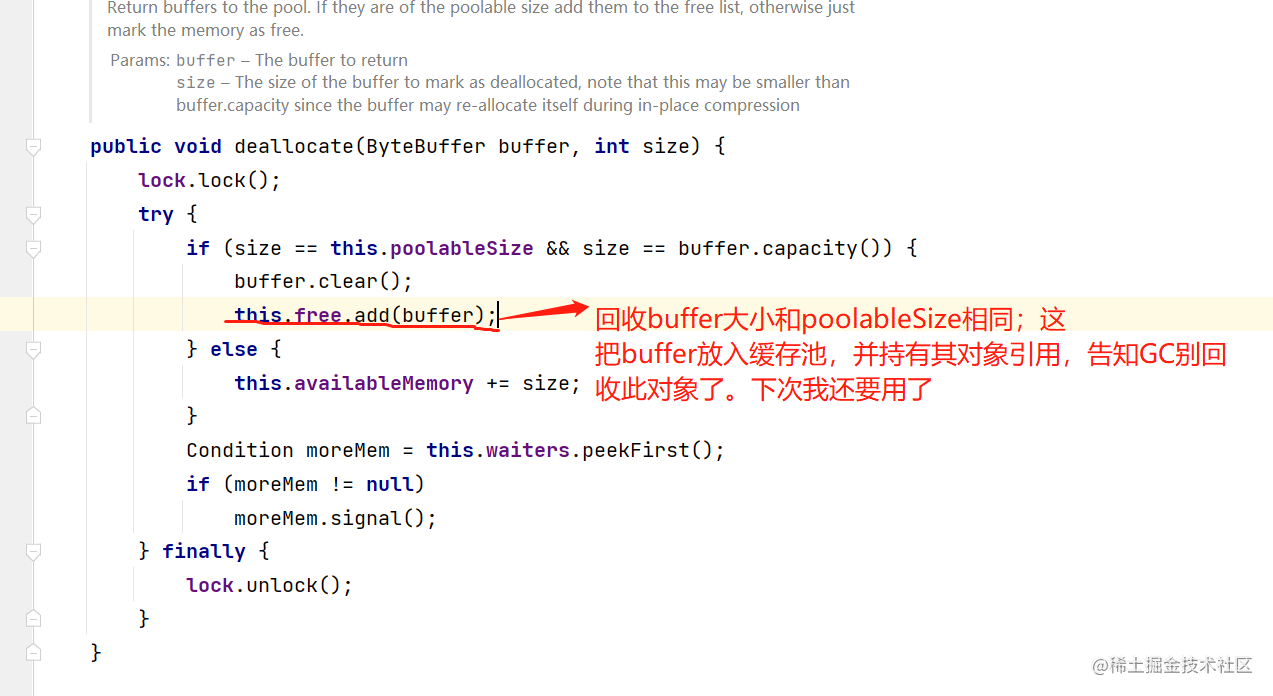
读kafka生产端源码,窥kafka设计之道(下)
背景 在上一篇文章《读kafka生产端源码,窥kafka设计之道(上)》 留下了kafka设计上比较优秀的一个点;内存的循环使用。本篇文章准备盘盘它。 好奇 为什么 kafka减少发送消息时向JVM频繁申请内存,就可以降低JVM GC的执…...
Pytorch个人学习记录总结 06
目录 神经网络-卷积层 torch.nn.Conv2d 神经网络-最大池化的使用 torch.nn.MaxPool2d 神经网络-卷积层 torch.nn.Conv2d torch.nn.Conv2d的官方文档地址 CLASS torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride1, padding0, dilation1, groups1, biasTrue,…...
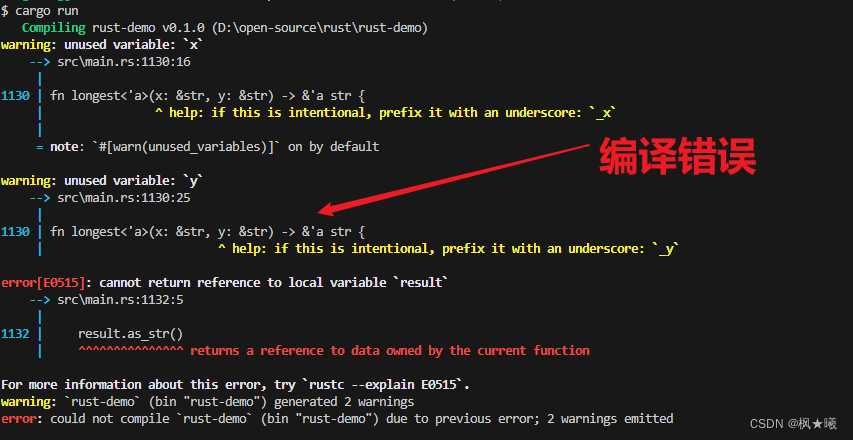
Rust之泛型、特性和生命期(四):验证有生存期的引用
开发环境 Windows 10Rust 1.71.0 VS Code 1.80.1 项目工程 这里继续沿用上次工程rust-demo 验证具有生存期的引用 生存期是我们已经在使用的另一种泛型。生存期不是确保一个类型具有我们想要的行为,而是确保引用在我们需要时有效。 我们在第4章“引用和借用”一…...
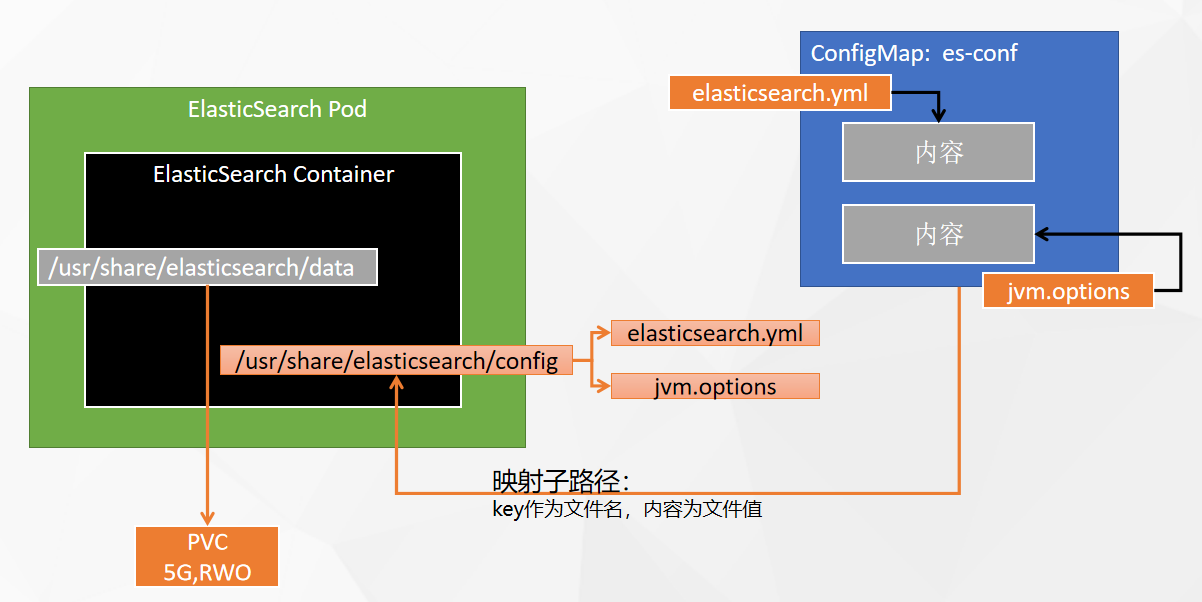
kubesphere安装中间件
kubesphere安装mysql 创建configMap [client] default-character-setutf8mb4[mysql] default-character-setutf8mb4[mysqld] init_connectSET collation_connection utf8mb4_unicode_ci init_connectSET NAMES utf8mb4 character-set-serverutf8mb4 collation-serverutf8mb4_…...
 集群模式安装)
zookeeper学习(二) 集群模式安装
前置环境 三台centos7服务器 192.168.2.201 192.168.2.202 192.168.2.150三台服务器都需要安装jdk1.8以上zookeeper安装包 安装jdk 在单机模式已经描述过,这里略过,有需要可以去看单机模式中的这部分,注意的是三台服务器都需要安装 安装…...
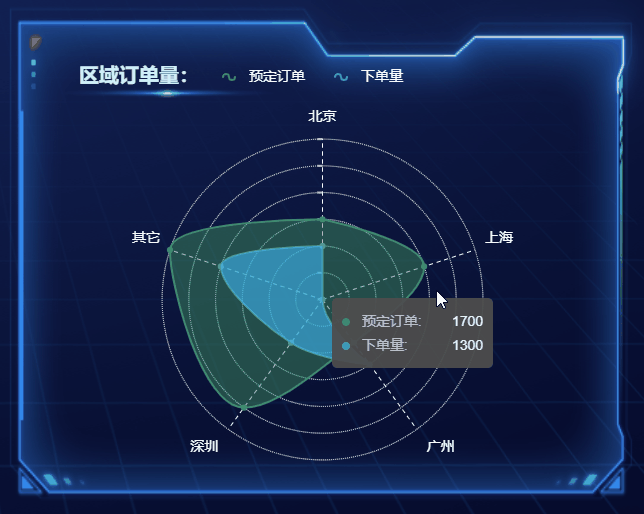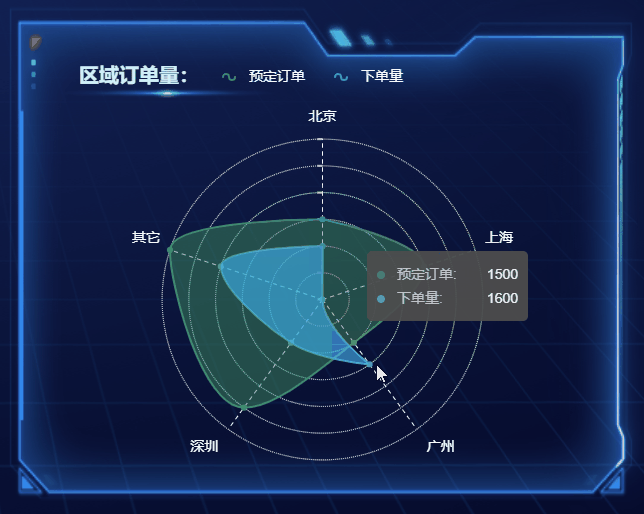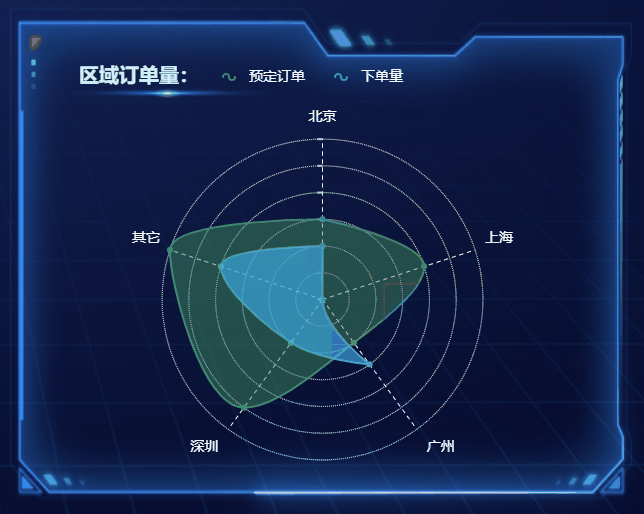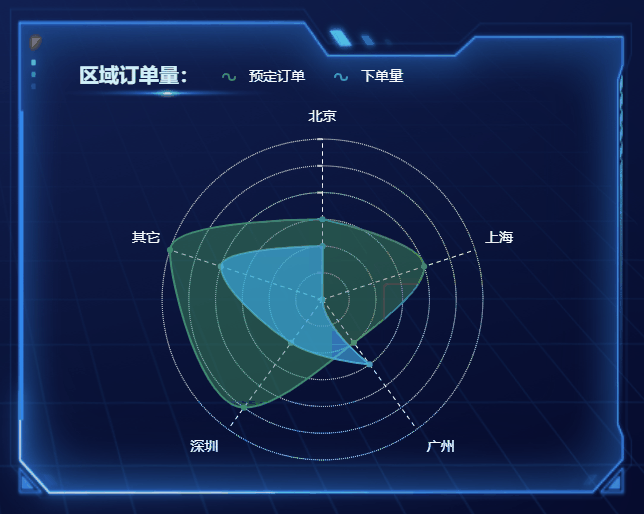
选择合适的图表,高效展现数据魅力
随着大数据时代的来临,数据的重要性愈发凸显,数据分析和可视化成为了决策和传递信息的重要手段。在数据可视化中,选择合适的图表是至关重要的一环,它能让数据更加生动、直观地呈现,为观众提供更有说服力的信息。本文将…...
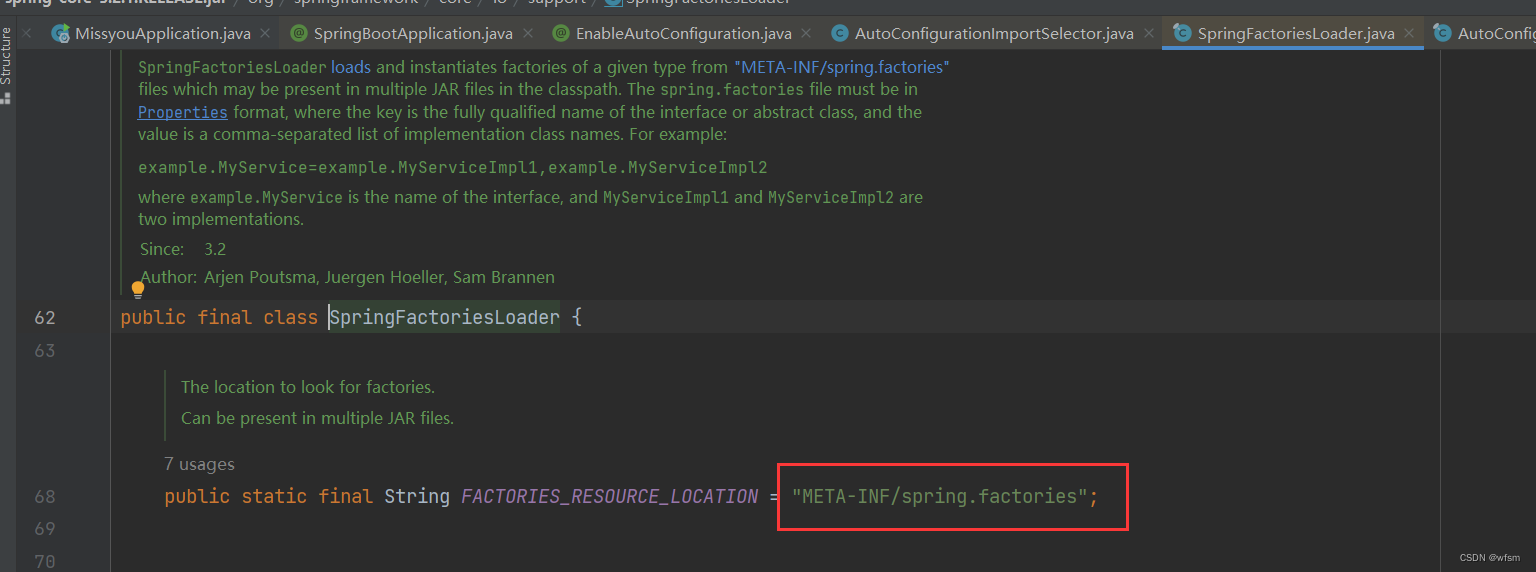
springboot自动装配
SPI spi : service provider interface : 是java的一种服务提供机制,spi 允许开发者在不修改代码的情况下,为某个接口提供实现类,来扩展应用程序 将实现类独立到配置文件中,通过配置文件控制导入ÿ…...

python小记-队列
队列(Queue)是一种常见的数据结构,它遵循先进先出(First-In-First-Out,FIFO)的原则。在队列中,新元素(也称为项)总是添加到队列的末尾,而最早添加的元素总是在…...
SpringBoot——持久化技术
简单介绍 在之前我们使用的数据层持久化技术使用的是MyBatis或者是MyBatis-plus,其实都是一样的。在使用之前,我们要导入对应的坐标,然后配置MyBatis特有的配置,比如说Mapper接口,或者XML配置文件,那么除了…...

Kafka 入门到起飞 - 生产者参数详解 ,什么是生产者确认机制? 什么是ISR? 什么是 OSR?
上回书我们讲了,生产者发送消息流程解析传送门 那么这篇我们来看下,生产者发送消息时几个重要的参数详解 ,什么是生产者确认机制? 什么是ISR? 什么是 OSR? 参数: bootstrap.servers : Kafka 集…...
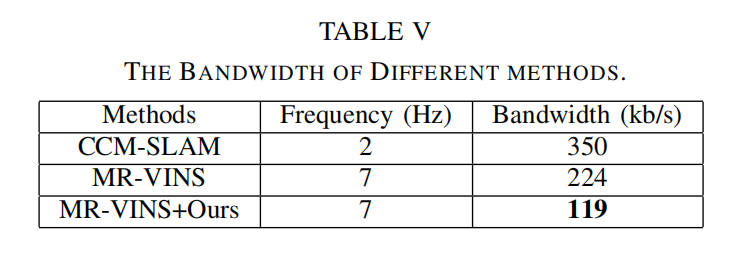
【文献分享】比目前最先进的模型轻30%!高效多机器人SLAM蒸馏描述符!
论文题目:Descriptor Distillation for Efficient Multi-Robot SLAM 中文题目:高效多机器人SLAM蒸馏描述符 作者:Xiyue Guo, Junjie Hu, Hujun Bao and Guofeng Zhang 作者机构:浙江大学CAD&CG国家重点实验室 香港中文大学…...
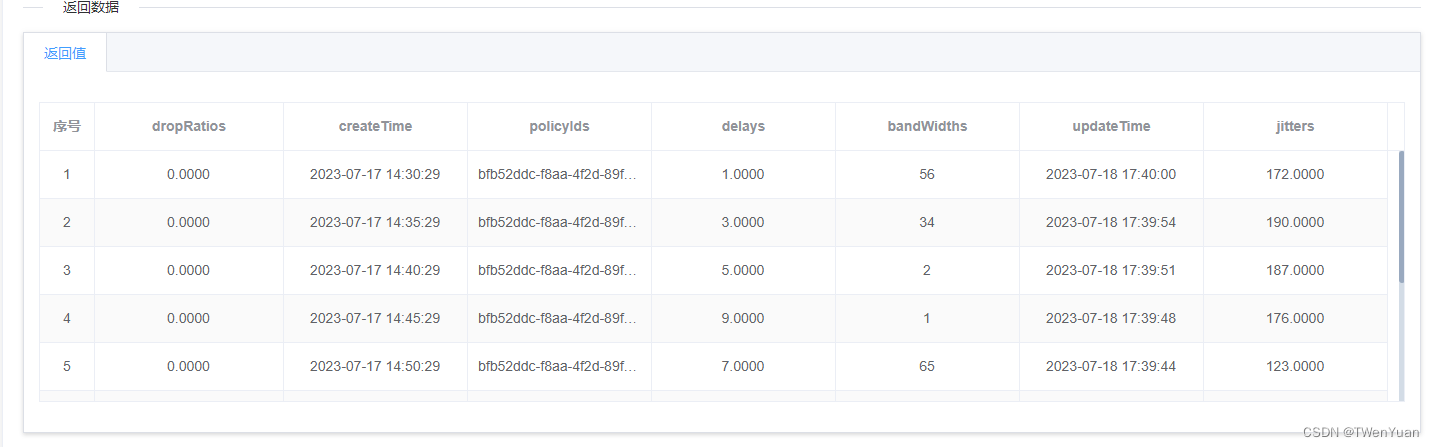
【数据动态填充到element表格;将带有标签的数据展示为文本格式】
一:数据动态填充到element表格; 二:将带有标签的数据展示为文本格式; 1、 <el-row><el-col :span"24"><el-tabs type"border-card"><el-tab-pane label"返回值"><el-…...

小程序轮播图的两种后台方式(PHP)--【浅入深出系列008】
微信目录集链接在此: 详细解析黑马微信小程序视频–【思维导图知识范围】难度★✰✰✰✰ 不会导入/打开小程序的看这里:参考 让别人的小程序长成自己的样子-更换window上下颜色–【浅入深出系列001】 文章目录 本系列校训学习资源的选择啥是轮播图轮播…...
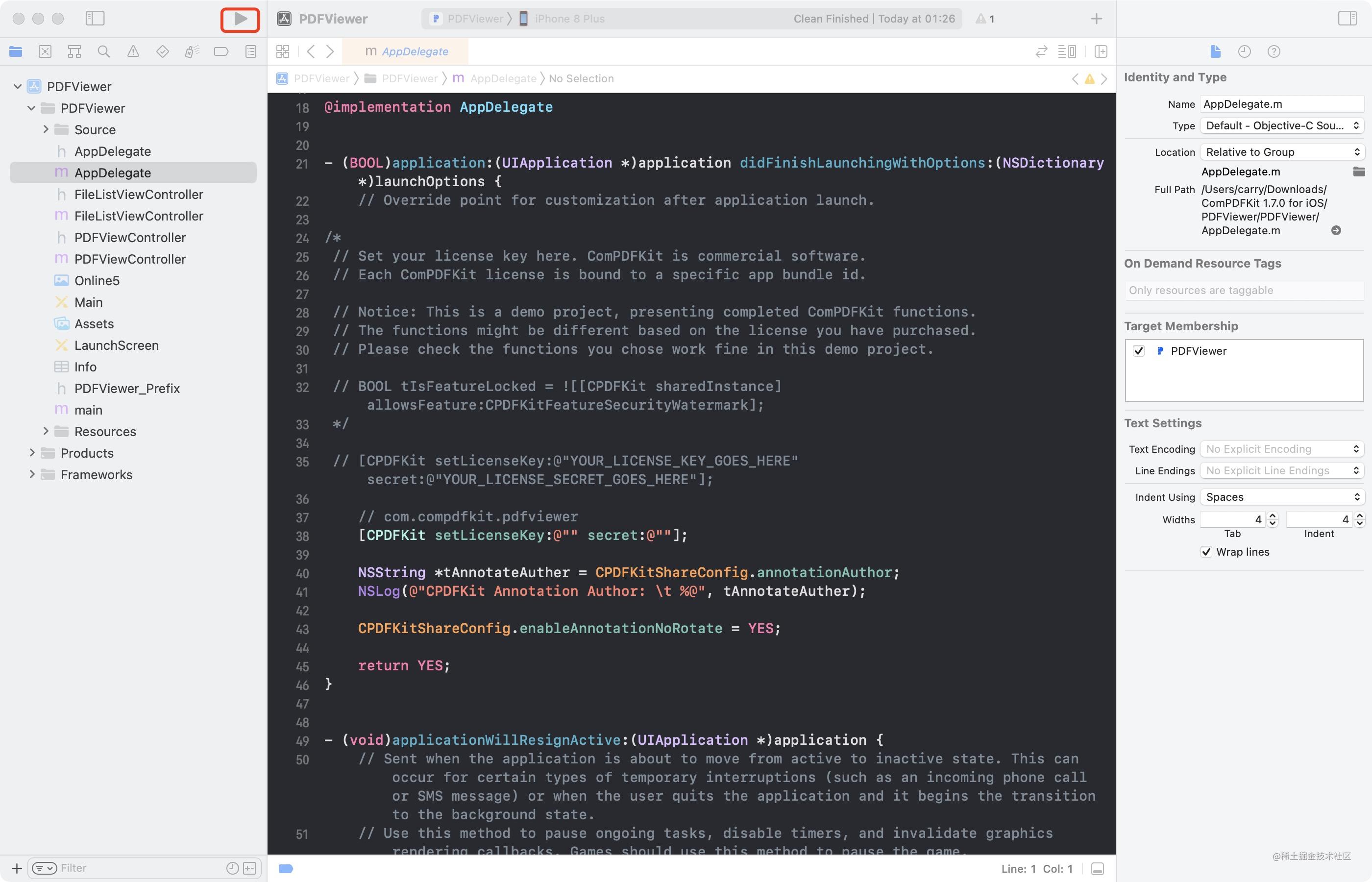
使用ComPDFKit PDF SDK 构建iOS PDF阅读器
在当今以移动为先的世界中,为企业和开发人员创建一个iOS应用程序是必不可少的。随着对PDF文档处理需求的增加,使用ComPDFKit这个强大的PDF软件开发工具包(SDK)来构建iOS PDF阅读器和编辑器可以让最终用户轻松查看和编辑PDF文档。 …...

一套流程6个步骤,教你如何正确采购询价
采购询价(RFQ)是一种竞争性投标文件,用于邀请供应商或承包商就标准化或重复生产的产品或服务提交报价。 询价通常用于大批量/低价值项目,买方必须提供技术规格和商业要求,该文件有时也称为招标书或投标邀请书。询价流…...

git使用
常用命令 git init git库初始化,初始化后会在文件中出现一个.git的隐藏文件 git clone 从远程克隆仓库 git pull 从远程库中拉取 git commit 将暂存提交到本地仓库 git push 提交本地仓库到远程 git branch 查看当前分支 git branch <branchName> 切换分支 …...
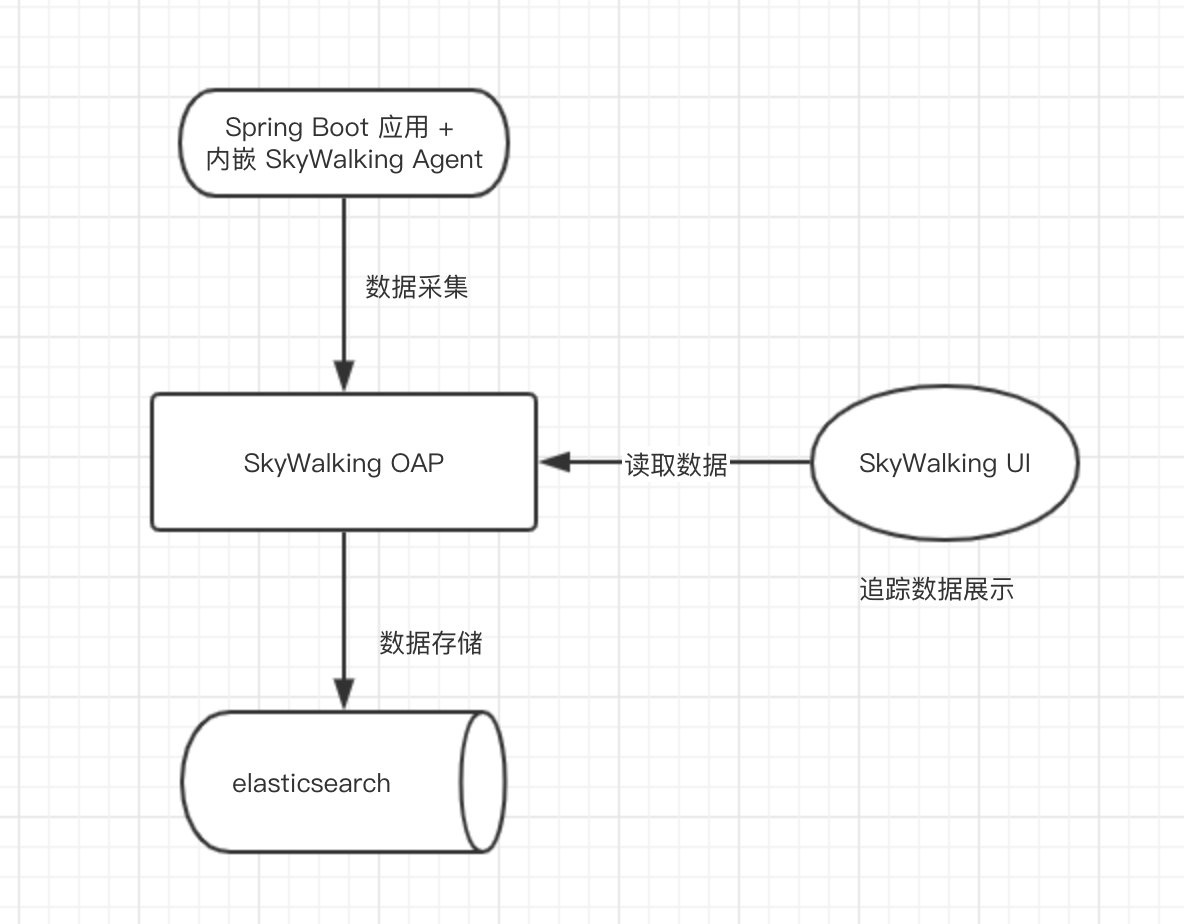
SkyWalking链路追踪-搭建-spring-boot-cloud-单机环境 之《10 分钟快速搭建 SkyWalking 服务》
首先了解一下单机环境 第一步,搭建一个 Elasticsearch 服务。第二步,下载 SkyWalking 软件包。第三步,搭建一个 SkyWalking OAP 服务。第四步,启动一个 Spring Boot 应用,并配置 SkyWalking Agent。第五步,…...
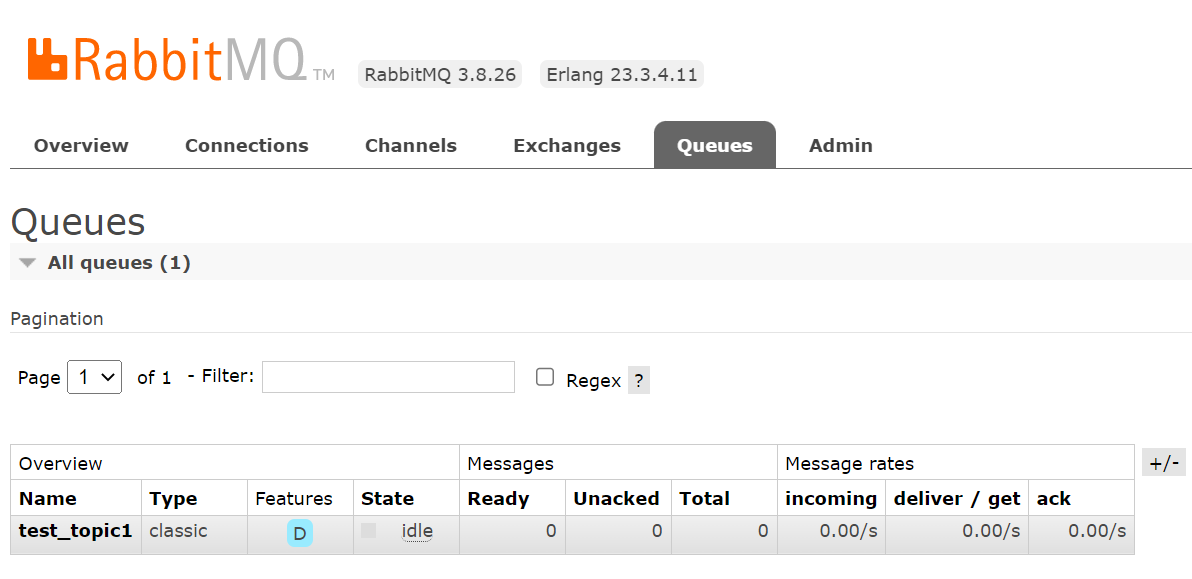
Rabbit MQ整合springBoot
一、pom依赖二、消费端2.1、application.properties 配置文件2.2、消费端核心组件 三、生产端3.1、application.properties 配置文件2.2、生产者 MQ消息发送组件四、测试1、生产端控制台2、消费端控制台 一、pom依赖 <dependency><groupId>org.springframework.boo…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...