怎样计算一个算法的复杂度?
分析一个算法主要看这个算法的执行需要多少机器资源。在各种机器资源中,时间和空间是两个最主要的方面。因此,在进行算法分析时,人们最关心的就是运行算法所要花费的时间和算法中使用的各种数据所占用的空间资源。算法所花费的时间通常称为时间复杂度,使用的空间资源称为空间复杂度。接下来学习如何计算一个算法的时间复杂度和空间复杂度。
1.时间复杂度
在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,然后分析T(n)随n的变化。
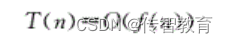
这样用大写的O来标记算法的时间复杂度,称之为大O(Order的简写)标记法。一般随着n的增长,T(n)也会随之增长,其中T(n
)增长最慢者就是时间性能最优的算法。
在计算时间复杂度的时候,根据T(n)与n的最高阶数关系,我们给这些算法的复杂度进行了归类,如表1所示。
当然还会有一些其他阶数关系,这里只是列出了几种较常见的关系。算法的执行次数可能会与规模n呈现出这些关系,那么这些关系又是如何推导出来的呢?下面给出大O阶的推导方法:
(1)用常数1取代运行中的所有加法常数。
(2)在修改后的运行次数函数中,只保留最高阶项。
(3)如果最高阶项存在,且不是1,则除去其常系数,得到的结果就是大O阶。
接下来通过分析几段程序的执行过程来推导出其时间复杂度,程序段1代码如下所示:
int a=100; //执行一次int b=200; //执行一次int sum=a+b; //执行一次printf("&d\n",sum); //执行一次
上述程序段有4行代码,每一行执行1次,加起来一共执行了4次,f(n)=4,即T(n)=O(4)。根据推导方法中的第一条,将常数项以1代替。在保留其最高阶项时,发现其没有最高阶项,因此该算法的时间复杂度为O(1),为常数阶。程序段2代码如下所示:
void func()
{int i,sum=0; //执行一次for (i=0;i<=100;i++){sum +=i; //执行n次}printf("sd\n",sum); //执行一次
}
该程序段的执行次数为1+n+1,则f(n)=n+2,即T(n)=O(n+2)。然后将常数项以1替换,且只保留最高阶项,则得出T(n)=O(n),因此该算法的时间复杂度为O(n),为线性阶。
程序段3代码如下所示:
void func()
{int i=l;do{i*=2;}while (i<n);
}
在这个程序段中,当i<n时,循环结束。如果循环了f(n)次,则2(fn)=n,即f(n)=log2n,T(n)=O(log2n)。然后消除常系数,保留最高阶项,最后得出T(n)=O(logn),为对数阶。
用大O阶来推导算法的复杂度并不难,读者在以后的学习中设计算法,就可以用此法来估测算法的优劣。
2.空间复杂度
空间复杂度是对一个算法在运行过程中所占存储空间大小的度量,一般也作为问题规模n的函数,以数量级形式给出,格式如下所示:

一个算法的存储量包括输入数据所占空间、程序本身所占空间和辅助变量所占空间。在对算法进行分析时,只考虑辅助变量所占空间。若所需辅助空间相对于输入数据量来说是常数,则称此算法为原地工作。若所用空间量依赖于特定的输入,则除了有特殊说明外,均按最坏情况考虑。
有时候,在写代码时可以用空间来换取时间,例如,写一个算法来判断某年是否是闰年,这样每输入一个年份都要调用算法去判断一下,在时间上就有点复杂。为了提高效率,可以用空间来换取时间,即建立一个大小合适的数据,编号从0到n,如果是闰年,则存入数据1,否则存入数据0。这样只要通过判断年份编号上存储的是0还是1就知道该年份是否是闰年了。
用空间换取时间可以将运算最小化,但这两种情况哪种更好,要结合具体情况而定。一般情况下,都是用时间复杂度来度量算法,当不加限定地使用“复杂度”这一术语时,都是指时间复杂度。
相关文章:

怎样计算一个算法的复杂度?
分析一个算法主要看这个算法的执行需要多少机器资源。在各种机器资源中,时间和空间是两个最主要的方面。因此,在进行算法分析时,人们最关心的就是运行算法所要花费的时间和算法中使用的各种数据所占用的空间资源。算法所花费的时间通常称为时…...

【问题记录】Ubuntu 22.04 环境下,打开 VS Code 老是访问密钥环该怎么解决?
目录 环境 问题情况 解决方法 环境 VMware Workstation 16 Pro (版本:16.1.2 build-17966106)ubuntu-22.04.2-desktop-amd64 问题情况 在Ubuntu下,每次运行 VS Code时,老是提示要输入密钥密码来解锁保存在密钥环&am…...
format格式化输出语法详解
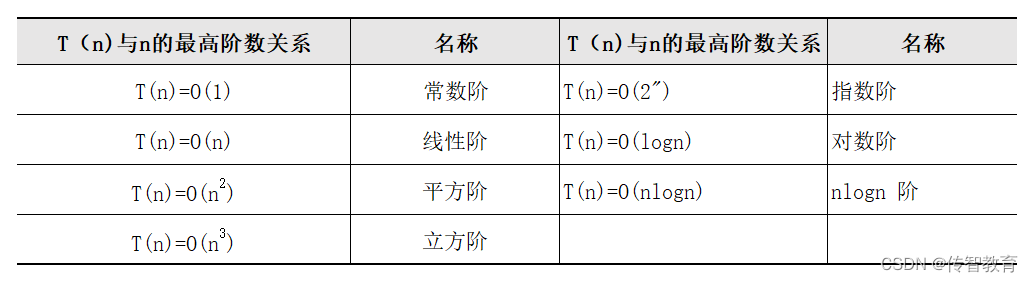
hello,这里是Token_w的文章,主要讲解python的基础学习,希望对大家有所帮助 整理不易,感觉还不错的可以点赞收藏评论支持,感谢! 使用 % 操作符对各种类型的数据进行格式化输出,这是早期 Python提…...

RocketMQ教程-(5)-功能特性-事务消息
事务消息为 Apache RocketMQ 中的高级特性消息,本文为您介绍事务消息的应用场景、功能原理、使用限制、使用方法和使用建议。 事务消息为 Apache RocketMQ 中的高级特性消息,本文为您介绍事务消息的应用场景、功能原理、使用限制、使用方法和使用建议。…...
HANA学习笔记
1、安装 准备安装介质,我这儿用的是HANA2.00.059.00,注意会用到三个lib包和saptune,提前准备好。 执行./hdblcm开启数据库安装,过程中会涉及到需要用户设置一些参数,按照自己需求设置即可。 安装完成会生成一个安装日…...
VMware虚拟机无法上网的解决办法
(1)1、在虚拟机右下角的网络适配器上面观察该图标是否是有绿色的灯在闪烁,如果网络适配器是灰色的证明虚拟机的网络没有打开,而是被禁用了,在适配器上点击鼠标右键,打开【设置】,在【已连接】、…...
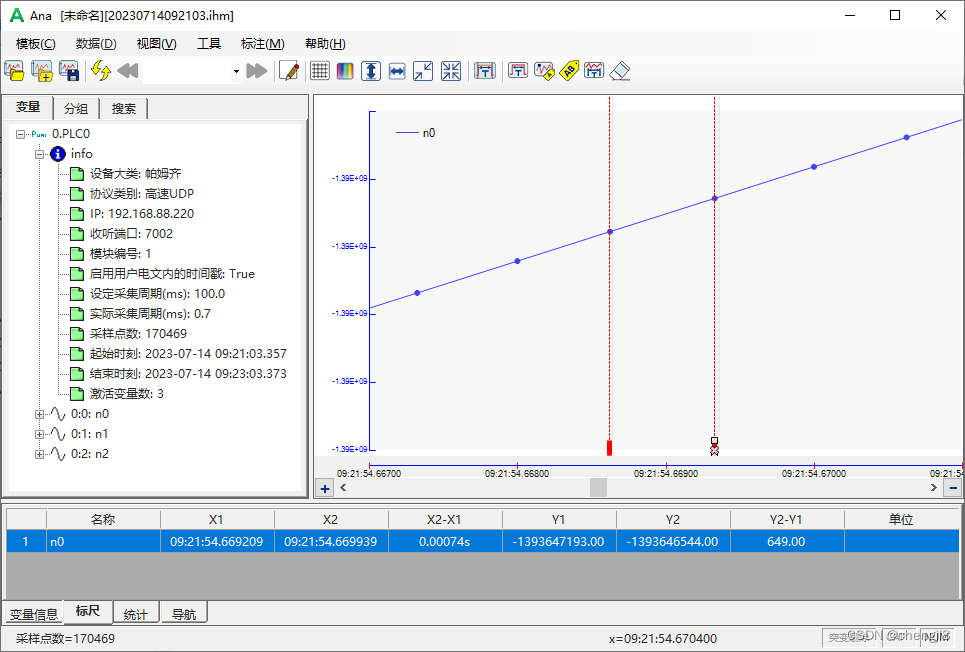
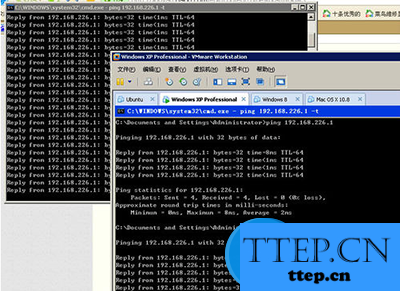
PLC-Recorder的高速采集有多快?0.5ms算快吗?看控制器能力了!
大家知道,PLC-Recorder有一个高速采集的功能,基于TCP连接或UDP报文,速度取决于发送端的能力。对于西门子PLC,能做到1-2ms的采集速度,但是,我在前面的文章里提到了0.5ms的高速采集,哪个控制器能这…...

KMP算法总结
KMP算法总结 BF算法引导BF算法步骤(图片演示)代码演示 KMP算法推next数组代码演示 BF算法引导 BF算法是一个暴力的字符串匹配算法,时间复杂度是o(m*n) 假设主串和子串分别为 我们想要找到子串在主串的位置 BF算法核…...

消息中间件ActiveMQ介绍
一、消息中间件的介绍 介绍 消息队列 是指利用 高效可靠 的 消息传递机制 进行与平台无关的 数据交流,并基于 数据通信 来进行分布式系统的集成。 特点(作用) 应用解耦 异步通信 流量削峰 (海量)日志处理 消息通讯 …... 应用场景 根据消息队列的特点&a…...

【100天精通python】Day9:数据结构_字典、集合
目录 目录 1 字典 1.1 字典的基本操作示例 1.2 字典推导式 2 集合 2.1 集合的常用操作示例 3 列表、元组、字典、集合的区别 1 字典 在Python中,字典(Dictionary)是一种无序的数据结构,用于存储键值对的集合。每个…...

上海VR全景展示,快速了解VR全景拍摄
导语: 随着科技的不断进步,虚拟现实技术的应用日益广泛。在这其中,VR全景图片作为一种数字化助力的全景拍摄方式,正逐渐成为人们关注的焦点。通过数字化技术,VR全景图片能够以360度全方位的视角呈现真实的场景&#x…...
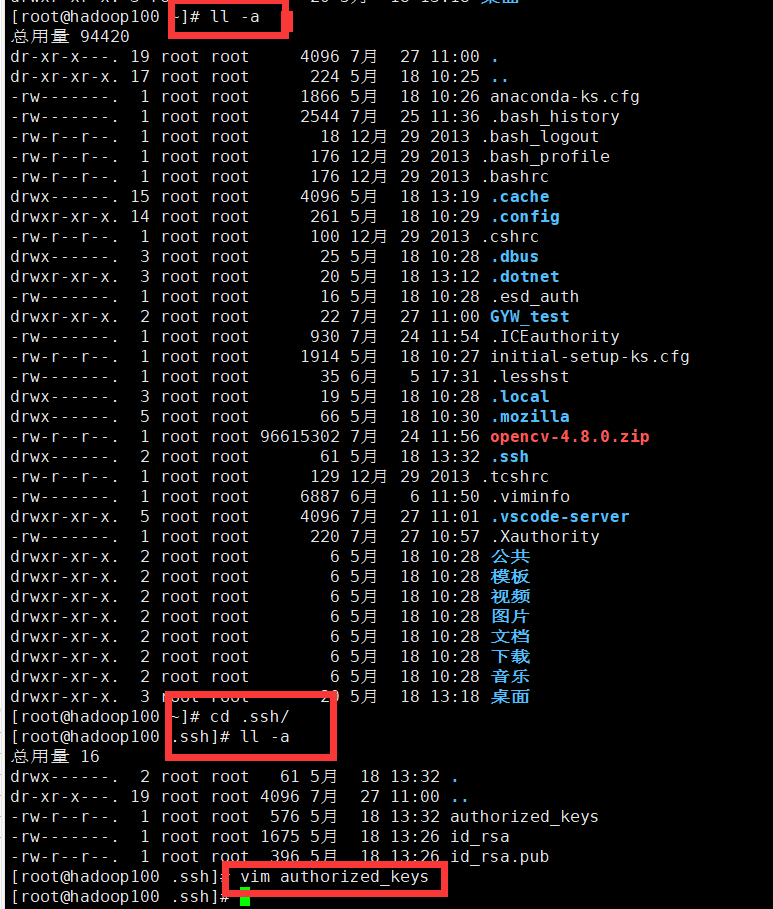
VScode远程不用再输入密码操作
安装插件remote development 1.先检查自己电脑上有没有生成一对公钥和私钥。(一般会在这个目录) 如果没有的话就自己生成一下。 打开命令行输入以下命令 ssh-keygen -t rsa2.在虚拟机中先看一下有没有公钥和私钥。如果没有的话就自己生成一下。 打开…...

MyBatis基本用法-@TableId
TableId 注解是 MyBatis Plus 框架中用于标识实体类中的主键字段的注解,它有一些可选的配置项。下面是详细说明: 首先,需要在项目中添加 MyBatis Plus 的依赖。可以在项目的 pom.xml 文件中添加以下代码: <dependency><…...

React AntDesign写一个导出数据的提示语 上面有跳转的路径,或者点击知道了,关闭该弹层
效果如下: 代码如下: ForwardDataCenterModal(_blank);export const ForwardDataCenterModal (target?: string) > {let contentBefore React.createElement(span, null, 数据正在处理中,请稍后前往);let contentAfter React.creat…...

小红书课程发光社群知识库,点亮哥专为超级个体设计解决方案
小红书课程点亮哥知识库 开创了学习小红书教育培训先河 针对超级个体轻创业的学习需求场景 创新推出了“知识库全新学习方式”。 一个人如何做好小红书? 超级个体轻创业,如何做好小红书? 通过打造个人IP、或者塑造老板个人品牌,来实现互联网变现,如何做好小红书? 就像挑…...

基于SpringBoot+Vue的摄影跟拍预定管理系统设计与实现(源码+lw+部署文档等)
博主介绍: 大家好,我是一名在Java圈混迹十余年的程序员,精通Java编程语言,同时也熟练掌握微信小程序、Python和Android等技术,能够为大家提供全方位的技术支持和交流。 我擅长在JavaWeb、SSH、SSM、SpringBoot等框架…...
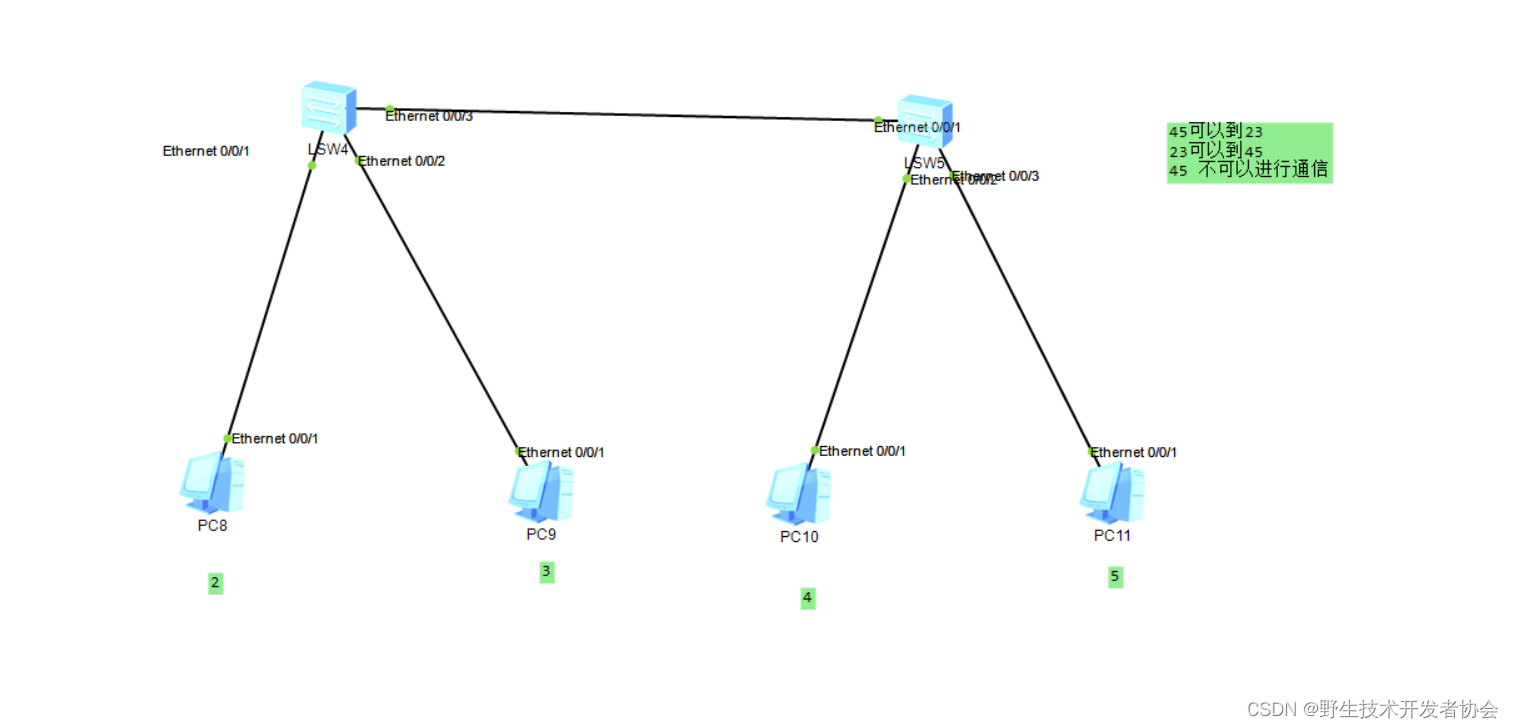
HCIA 第二课总结
配置网络设备的明文密钥实验组网 实验拓扑 将一个路由器使用配置口进行连接 sys #进入系统视图模式 sysname RTA #给设备命名 user-interface console 0 #进入用户接口配置界面 authentication-mode password #配置认证模式为密钥认证 set authentication password ciphe…...

linux-------联网下载文件和配置
1.Wget Wget是一个十分常用命令行下载工具,多数Linux发行版本都默认包含这个工具。如果没有安装可在http://www.gnu.org/software/wget/wget.html下载最新版本,并使用如下命令编译安装: 1.#tar zxvf wget-1.9.1.tar.gz #cd wget-1.9.1 #./c…...
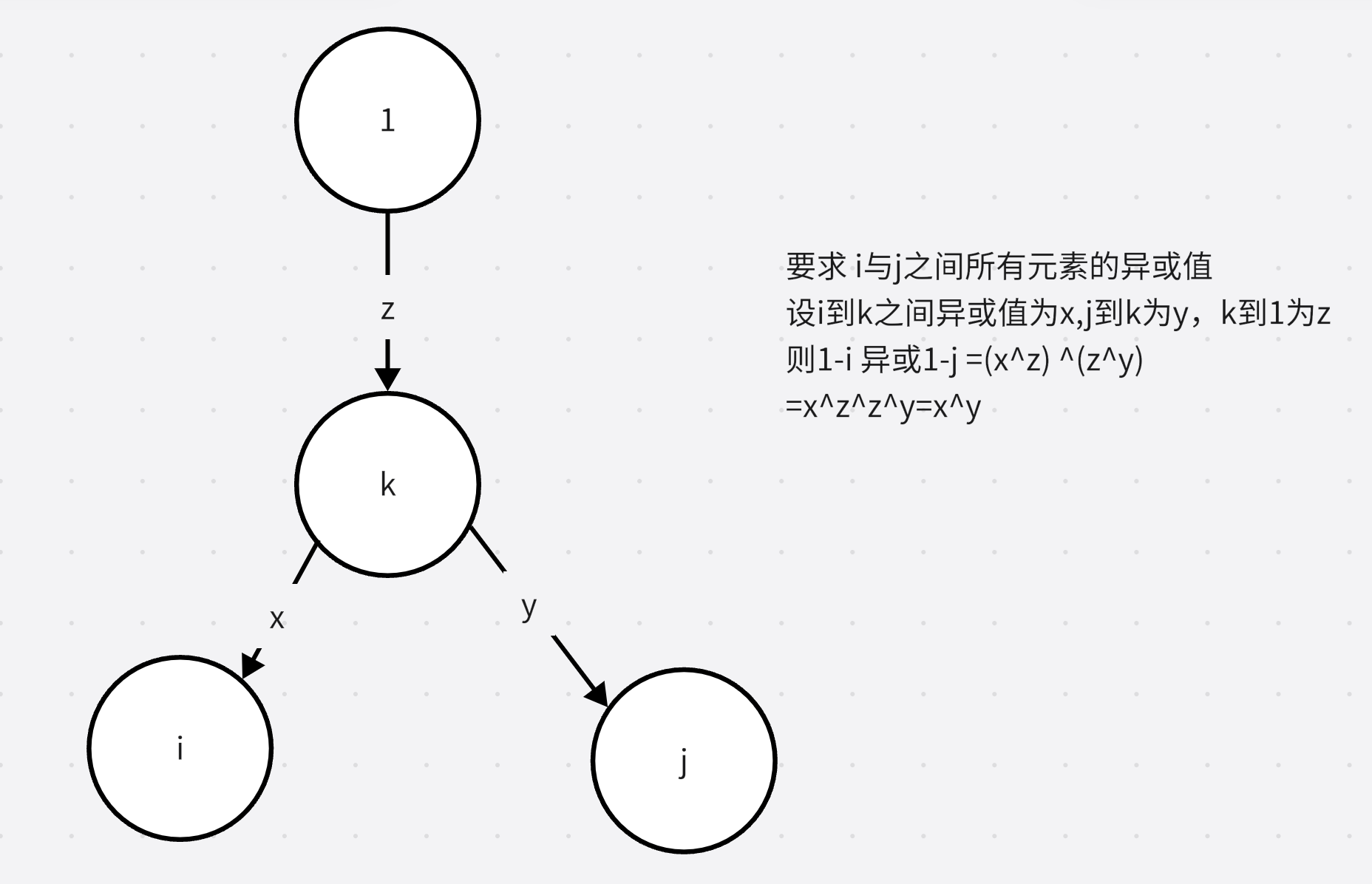
字典树Trie
Trie树又称字典树,前缀树。是一种可以高效查询前缀字符串的树,典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。 它的优点是:利用字符串…...

算法之桶排序算法
桶排序的基本思想是: 把数组 arr 划分为 n 个大小相同子区间(桶),每个子区间各自排序,最 后合并 。计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况。 1.找出待排序数组中的…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
