数据结构--线性表2-1
目录
一、线性结构的定义
二、线性表的表示
三、顺序表的实现(或操作)
1、修改:
2、插入:
四、顺序表的运算效率分析:时间效率分析:
一、线性结构的定义
若结构时非空有限集,则有且仅有一个开始结点和一个终端结点,并且所有结点都最多只有一个直接前驱和一个直接后继。可表示为:(a1,a2,a3,……,an)
1,2,3,……,n:下标,即元素的序号,表示元素在表中的位置。
n为元素总个数,即表长。n>=0。当n=0时,称为 空表。
特点1、只有一个首结点和尾结点;
特点2、除首尾结点外,其它结点只有一个直接前驱和一个直接后继。
线性结构包括:线性表、堆栈、队列、字符串、数组等。其中最典型、最常用的是-----线性表。
注意:同一线性表中的元素必定具有相同特性!
二、线性表的表示
线性表的顺序表示又称为顺序存储结构或顺序映像。
顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。
特点:逻辑上相邻的元素,物理上也相邻。
顺序存储方法:用一组地址连续的存储单元一次存储线性表的元素。
例如,可以利用数组V[n]来实现。
注意:在C语言中数组的下标是从0开始的,即:V[n]的有效范围是从V[0]~V[n-1]。
三、顺序表的实现(或操作)
数据结构的基本操作: 修改、插入、删除、查找、排序
1、修改:
通过数组的下标便可访问某个特定的元素并修改之。核心语句:V[i]=x;
显然,顺序表修改操作的时间效率是O(1)。
2、插入:
在线性表的第i个位置前插入一个元素
实现步骤:(1) 将第n至第i位的元素向后移动一个位置;
(2) 将要插入的元素写到第i个位置;
(3) 表长加1。
注意:事先应判断:插入位置i是都合法?表里是否已满?
应当符合条件:1<=i<=n+1 或 i = [1,n+1]
核心语句:
for(j=n;j>=1;j--)
a[j+1]=a[j];
a[i]=x;
n++;
将上述插入与删除写完整:
#include <stdio.h>
#include <stdlib.h>
#define N 100
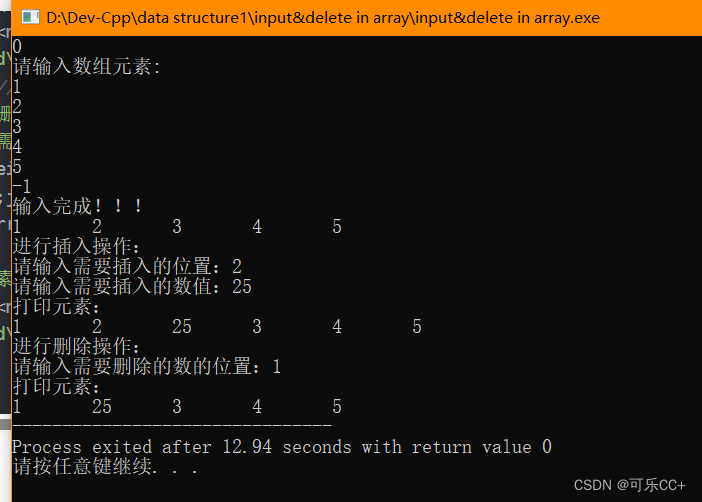
int arry[]={};int main()
{int num=0;int num1=0;int wei;printf("%d\n",arry[num]);printf("请输入数组元素:\n");while(arry[num]>=0){num=num1;scanf("%d",&arry[num]);num1++;}printf("输入完成!!!\n");for(int i=0;i<num;i++){printf("%d\t",arry[i]);}num1=0;
插入操作 num1为需要插入的数据wei,位置 printf("\n进行插入操作:\n");printf("请输入需要插入的位置:");scanf("%d",&wei);if(wei<0||wei>num){printf("位置输入错!!!");exit(0); }else{printf("请输入需要插入的数值:");scanf("%d",&num1); for(int j=num;j>=wei;j--){arry[j+1]=arry[j];}num++;arry[wei]=num1;}printf("打印元素:\n");for(int i=0;i<num;i++)printf("%d\t",arry[i]);
///删除操作///wei需要删除的位置 printf("\n进行删除操作:\n");printf("请输入需要删除的数的位置:");scanf("%d",&wei);for(int j=wei;j<num;j++)arry[j]=arry[j+1];num--;printf("打印元素:\n");for(int i=0;i<num;i++)printf("%d\t",arry[i]); return 0;
} 
四、顺序表的运算效率分析:
时间效率分析:
算符时间主要耗费在移动元素的操作上,因此计算时间复杂度的基本操作(最深层语句频度)
T(n)= o (移动元素的次数)
而移动元素的个数取决于插入或删除元素的位置。
假如:若在长度为n的线性表的第i位前插入一个元素,则向后移动元素的次数f(n)为:
f(n)= n-i+1;
若插入在尾结点之后,则根本无需移动(特别快)
若插入在首结点之前,则表中元素全部要后移(特别慢)
应当考虑各种未知插入(共n+1种可能)的平均次数才合理。
推导:假定在每个元素未知上插入x的可能性都一样。
若在首结点前插入,需要移动的元素最多,后移次数为n;
若在a(1)后面插入,则需要移动n-1个元素,后移次数为n-1;
……
若在a(n-1)后面插入,则需要移动1个元素,后移次数为1;
若在a(n)后面插入,则需要移动0个元素,后移次数为0;
所有可能的元素移动次数合计:0+1+2+……+n-1+n = (n+0)(n+1)/2
共有n+1(连头带尾)种插入形式!!!
故插入时的平均移动次数为:n(n+1))/2 ÷(n+1)=n/2≈ O(n) 【n只跟次数有关与前面的系数无关】。
同理,推导出顺序表删除一元素的时间效率为:T(n)= (n-1)/2≈O(n)。
总结:对于顺序表,插入、删除操作平均需要移动一半元素(n/2),时间的复杂度为O(n)。由于在操作时,只需要提供辅助变量,因此空间复杂度为O(1)。
相关文章:

数据结构--线性表2-1
目录 一、线性结构的定义 二、线性表的表示 三、顺序表的实现(或操作) 1、修改: 2、插入: 四、顺序表的运算效率分析:时间效率分析: 一、线性结构的定义 若结构时非空有限集,则有且仅有一个…...
网访问内网机器:基于frp的内网穿透
随缘更新些我自己的博客网站里的文章吧 因为经常需要远程访问自己的机器,所以写一个博客记录一下 公网访问内网机器:基于frp的内网穿透 从公网中访问自己的私有设备向来是一件难事儿。 1. 为什么需要内网穿透? A. 计算机网络 如何在自己的机…...
【Spring框架】Spring读取与存储综合练习
练习 在 Spring 项⽬中,通过 main ⽅法获取到 Controller 类,调⽤ Controller ⾥⾯通过注⼊的⽅式调⽤ Service 类,Service 再通过注⼊的⽅式获取到 Repository 类,Repository 类⾥⾯有⼀个⽅法构建⼀个 User 对象,返…...
Python实现指定区域桌面变化监控并报警
在这篇博客中,我们将使用Python编程语言和一些常用的库来实现一个简单的区域监控和变化报警系统。我们将使用Tkinter库创建一个图形界面,允许用户选择监控区域,并使用OpenCV库进行图像处理和相似性比较,以检测区域内的变化&#x…...
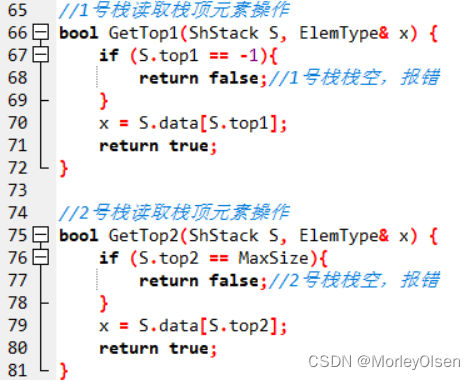
【数据结构】实验五:栈
实验五 栈 一、实验目的与要求 1)熟悉栈的类型定义和基本操作; 2)灵活应用栈解决具体应用问题。 二、实验内容 1、判断回文数,回文是指正读反读均相同的字符序列,如“1221”和“12321”均是回文,但“…...

⚡️⚡️Java多线程编程的高效、安全实践
⚡️ Java多线程编程的高效、安全实践⚡️ ☀️ 1 摘要☀️2 多线程编程基础☀️ 3 线程同步与互斥☀️ 4 并发集合类与原子操作☀️ 5 线程池与执行器框架☀️ 6 并发编程的最佳实践🌄 7 总结 博主 默语带您 Go to New World. ✍ 个人主页—— 默语 的博客…...

【云原生】Docker私有仓库registry
目录 1)用docker容器运行registry私有仓库服务。 2)运行私有仓库服务 3)镜像重命名(要上传的镜像名需要注明私仓的ip) 4)编辑docker配置文件(因为默认是拉取docker官方的镜像,需要重新指定) 5)其他dock…...

第十四届蓝桥杯大赛青少年省赛C++组试题真题 2023年5月
一、选择题 第 1 题 单选题 C中,bool类型的变量占用字节数为 ( )。 A. 1 B. 2 C. 3 D. 4 第 2 题 单选题 以下关于C结构体的说法,正确的是 ( )。 A. 结构体中只能包含成员变量,不能包含成员函数 B. 结构体不能从另一个结构体继承 …...
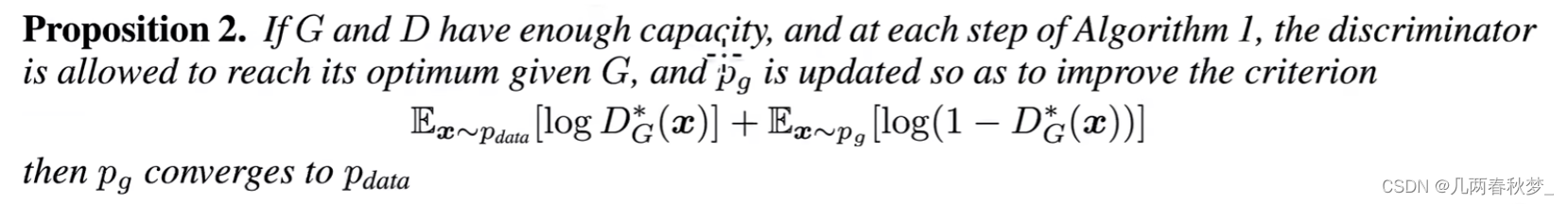
GAN论文精读
标题:Generative Adversarial Nets 摘要: 简写:作者提出了一个framework通过一个对抗的过程,在这里面会同时训练两个模型。 第一个模型为生成模型G,是用来抓住整个数据的分布 第二个模型为辨别模型D,是用来估计一个样本是否从G中产生。 …...
)
数据结构:计数排序(详解)
思路详解: 1 找到数组中的最大值、最小值 2 开辟一个统计每个数据出现次数的数组(总个数是最大值-最小值1,因为下标范围是0~最大值-最小值,闭区间统计个数要1) 3 遇到一个元素,在此元素-最小值作为下标的…...

1 请使用js、css、html技术实现以下页面,表格内容根据查询条件动态变化。
1.1 创建css文件,用于编辑style 注意: 1.背景颜色用ppt的取色器来获取: 先点击ppt的形状轮廓,然后点击取色器,吸颜色,然后再点击形状轮廓的其他轮廓颜色,即可获取到对应颜色。 2.表格间的灰色线…...
react-native项目安卓版本升级 compileSdkVersion 29->31
因为 react-native-ble-manager添加过程及碰到的问题 依赖 https://github.com/innoveit/react-native-ble-manager 参考:https://blog.csdn.net/withings/article/details/71378562 iOS 按react-native-ble-manager 文档在 【Info.plist】加了key之后能正常使用…...
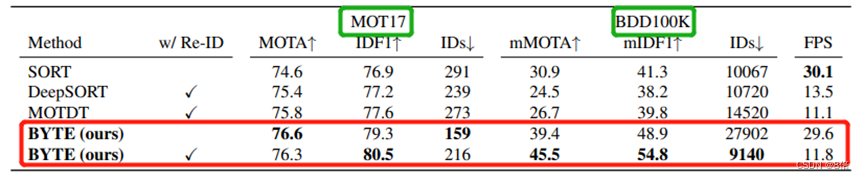
【学习笔记】目标跟踪领域SOTA方法比较
目录 前言方法1 TraDeS:2 FairMOT:3 SMILEtrack:4 ByteTrack: 前言 常用于行人跟踪的多目标跟踪数据集包括:MOT 15/16/17/20、PersonPath22等… 为更好比较现有SOTA算法的检测性能,本博客将针对在各数据集上表现较优的算法模型进行介绍。(表…...
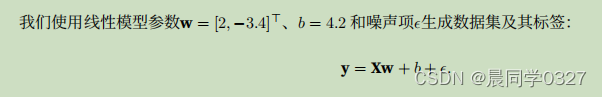
机器学习 深度学习编程笔记
sigmoid函数 def sigmoid(x):return 1.0 / (1np.exp((-x)))定义最小平方和损失函数 loss torch.nn.MSELoss()线性回归编程 如果不加噪音就成了正常的线性函数了,所以要加噪音。 torch.normal(0, 0.01, y.shape)torch.normal(0, 0.01, y.shape)是一个用于生成服从…...

18.背景轮播
背景轮播 html部分 <div class"container"><div class"slide active" style"background-image: url(./static/20180529205331_yhGyf.jpeg);"></div><div class"slide " style"background-image: url(./s…...
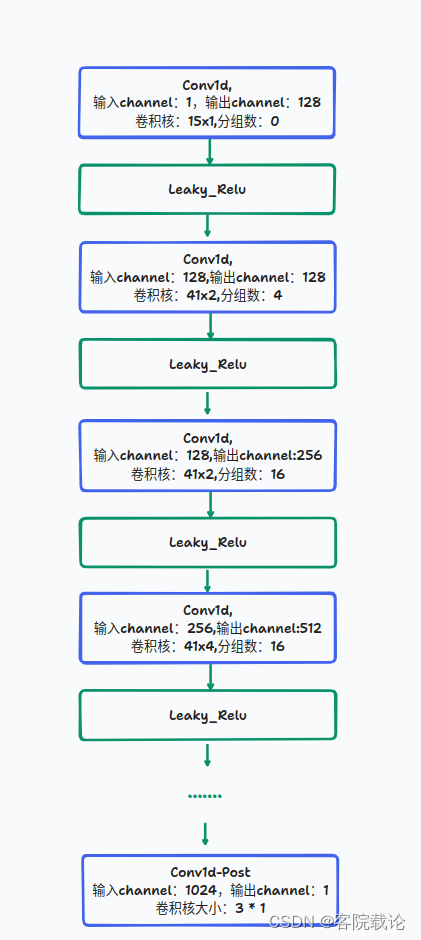
论文代码学习—HiFi-GAN(2)——鉴别器discriminator代码
文章目录 引言正文鉴别器多周期鉴定器多尺度鉴定器问题 总结 引言 这里翻译了HiFi-GAN这篇论文的具体内容,具体链接。这篇文章还是学到了很多东西,从整体上说,学到了生成对抗网络的构建思路,包括生成器和鉴定器。细化到具体实现的…...
 grep命令】)
Linux Shell 脚本编程学习之【第3章 正则表达式 (第二部分) grep命令】
第3章 正则表达式 (第二部分) 4 grep命令4.1 基本用法4.2 参考命令4.2.1 双引号4.2.2 -c 输出匹配行数4.2.3 -h 或 -l 不显示或只显示文件名4.2.4 -s 不显示错误信息4.2.5 -r 递归显示本级目录及下级目录4.2.6 -w 匹配完整词 -x 匹配完整行4.2.7 -q 退出…...
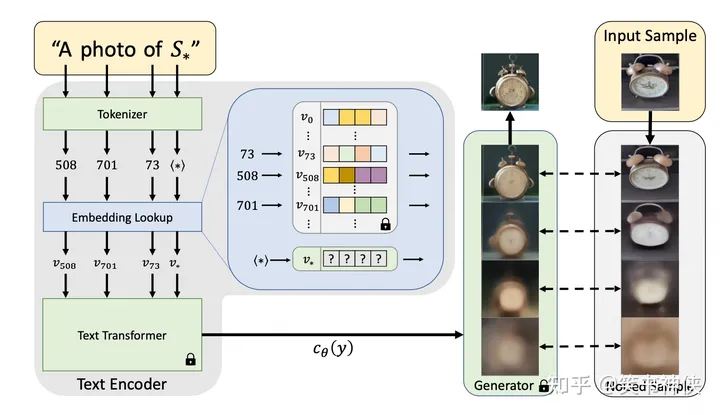
大语言模型LLM
目录 一、语言模型的发展 语言模型(Language Model,LM)目标是建模自然语言的概率分布,具体目标是构建词序列w1,w2,...,wm的概率分布,即计算给定的词序列作为一个句子出现可能的大小P(w1w2...wm)。但联合概率P的参数量…...

自学网络安全(黑客)的误区
前言 网络安全入门到底是先学编程还是先学计算机基础?这是一个争议比较大的问题,有的人会建议先学编程,而有的人会建议先学计算机基础,其实这都是要学的。而且这些对学习网络安全来说非常重要。 一、网络安全学习的误区 1.不要…...
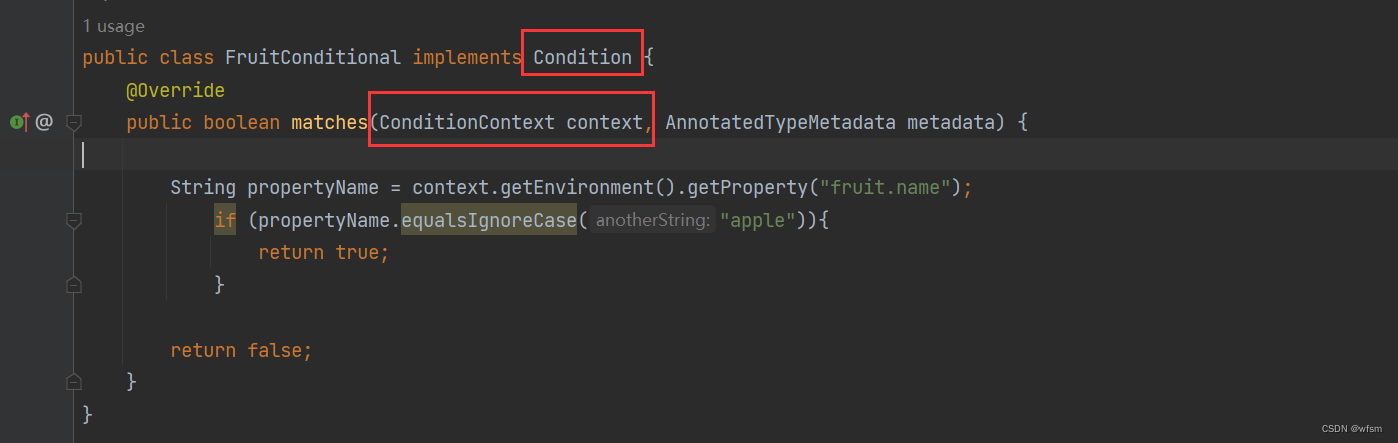
@Conditional
Conditional Conditional 是 spring framework 中提供的一个条件注解,,满足条件就注入,不满足就不注入ioc Condtional 需要和 Condition接口 一起用: 返回true注入,返回false不注入,, 里面有一…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
