【数据挖掘】时间序列的傅里叶变换:用numpy解释的快速卷积
一、说明
二、FFT的历史根源
傅里叶变换算法被认为是所有数学中最伟大的发现之一。法国数学家让-巴蒂斯特·约瑟夫·傅立叶在1822年的《Théorie analytique de la chaleur》一书中为调和分析奠定了基础。

法国数学家让·巴蒂斯特·约瑟夫·傅立叶(1768-1830 年)的雕刻肖像,19 世纪初。[来源:维基百科,图片来自公共领域]
这个奇妙的框架还为分析时间序列提供了很好的工具......这就是我们在这里的原因!
这篇文章是傅里叶变换系列文章的一部分。今天我们将讨论卷积以及傅里叶变换如何提供最快的方法。
三、离散傅里叶变换 (DFT) 的定义
让我们从基本定义开始。N 个元素的离散时间序列 x 的离散傅里叶变换为:
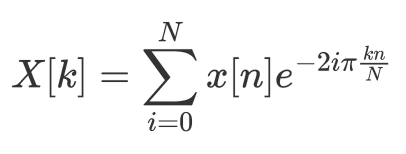
离散傅里叶变换 (DFT) 定义。存在其他定义,您只需要选择一个并坚持下去(由作者制作)
其中 k 表示 x 频谱的第 k 个频率。请注意,一些作者在该定义中添加了 1/N 的比例因子,但对这篇文章来说并不重要——总而言之,这只是一个定义问题并坚持下去。
然后是傅里叶逆变换(给定前向傅里叶变换的定义):
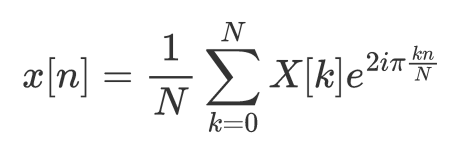
逆离散傅里叶变换,基于上述前向定义(由作者制作)。
话虽如此,傅里叶变换最重要的定理之一是一个空间中的卷积等价于另一个空间中的乘法。换句话说,乘积的傅里叶变换是相应傅里叶谱的卷积,卷积的傅里叶变换是相应傅里叶谱的乘积。
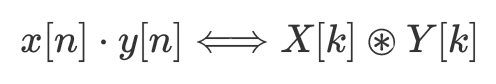
时域中的乘法对应于傅里叶域中的循环卷积(由作者制作)。
和

时域中的循环卷积对应于傅里叶域中的乘法(由作者制作)。
其中点表示标准乘积(乘法),圆圈星表示圆形卷积。
两个重要注意事项:
- 周期信号:傅里叶分析框架认为我们处理的信号是周期性的。换句话说,它们从负无穷大重复到无穷大。然而,使用有限的内存计算机处理此类信号并不总是实用的,因此我们只“玩”一个周期,我们将在后面看到。
- 循环卷积:卷积定理指出乘法等价于循环卷积,这与我们更习惯的线性卷积略有不同。正如我们将看到的,它并没有那么不同,也没有那么复杂。
四、循环卷积与线性卷积
如果您熟悉线性卷积(通常简称为“卷积”),那么您不会被循环卷积混淆。基本上,循环卷积只是卷积周期信号的方法。正如您可以猜到的,线性卷积仅对有限长度的信号有意义,这些信号的范围不是从负无穷大到无穷大。在我们的例子中,在傅里叶分析的上下文中,我们的信号是周期性的,因此不满足这个条件。我们不能谈论(线性)卷积。
然而,我们仍然可以直观地对周期信号进行线性卷积式操作:只需将周期信号卷积在一个周期长度上即可。这就是循环卷积的作用:它在一个周期跨度上卷积 2 个相同长度的周期信号。
为了进一步说服自己差异,请比较离散线性卷积和离散循环卷积的两个公式:

线性卷积方程:大多数时候在信号处理中,使用此公式,通过填充零(由作者制作)。
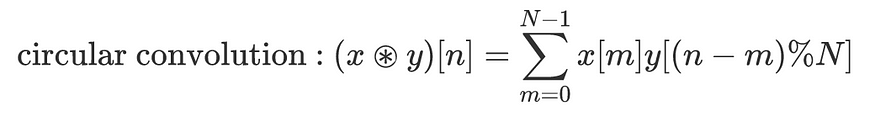
循环卷积 :这是处理周期信号时使用的卷积,如傅里叶分析(由作者制作)。
注意差异:
- 边界:线性卷积使用从负无穷大到正无穷大的样本 — 如前所述,在这种情况下,x 和 y 具有有限的能量,总和是有意义的。对于循环卷积,我们只需要在一个时间段内发生了什么,所以总和只跨越一个周期
- 循环索引 :在循环卷积中,我们使用长度为 N 的模运算“包装”y 的索引。这只是一种确保 y 被认为是周期为 N 的周期的方法:当我们想知道位置 k 处 y 的值时,我们只在位置 k%N 处使用 y 的值 — 因为 y 是 N 周期性的,我们得到正确的值。同样,这只是处理周期性无限长度样本序列的一种数学方法。
五、在 numpy 中的实现
Numpy为有限长度信号提供了很好的工具:这是一个好消息,因为正如我们刚刚看到的,我们的无限长度周期信号可以用一个周期来表示。
让我们创建一个简单的类来表示这些信号。我们添加了一个快速绘制数组的方法,以及“基本”数组前后的额外周期,以记住我们正在处理周期序列。
import numpy as np
import matplotlib.pyplot as pltclass PeriodicArray:"""A class to represent a periodic signal, using a singleperiod of the sequence."""def __init__(self, base):"""base is the base sequence representing a full period."""self.base = base@propertydef N(self): """Lenght of the base array, which is also the period of our infinite-periodic sequence"""return len(self.base)def __getitem__(self, n):"""We can get the value at any index, from -infinityto +infinity using the fact that the sequence is N-periodic, so we use the modulo operator.Examples-------->>> x = PeriodicArray([1, 2, 3])>>> x[0]1>>> x[4]2>>> x[5]3"""return self.base[n%self.N]def plot(self, ax=None):"""Quickly plot the sequence, with a period before and afterthe base array."""if ax is None:fig, ax = plt.subplots()line = ax.plot(self.base, '-o')ax.plot(np.arange(-self.N, 0), self.base, '--o', color=line[0].get_color(), alpha=0.5)ax.plot(np.arange(self.N, self.N*2), self.base, '--o', color=line[0].get_color(), alpha=0.5)return ax让我们看两个例子:首先是采样的窦序列,然后是线性序列。两者都被认为是 N 周期性的(在这种情况下为 N=10)。
periodic_sampled_sinus = PeriodicArray(np.sin(2*np.pi*1*np.linspace(0, np.pi/10, 10)))
periodic_sampled_sinus.plot()periodic_slope = PeriodicArray(np.linspace(-5, 5, num=10)*0.5)
periodic_slope.plot()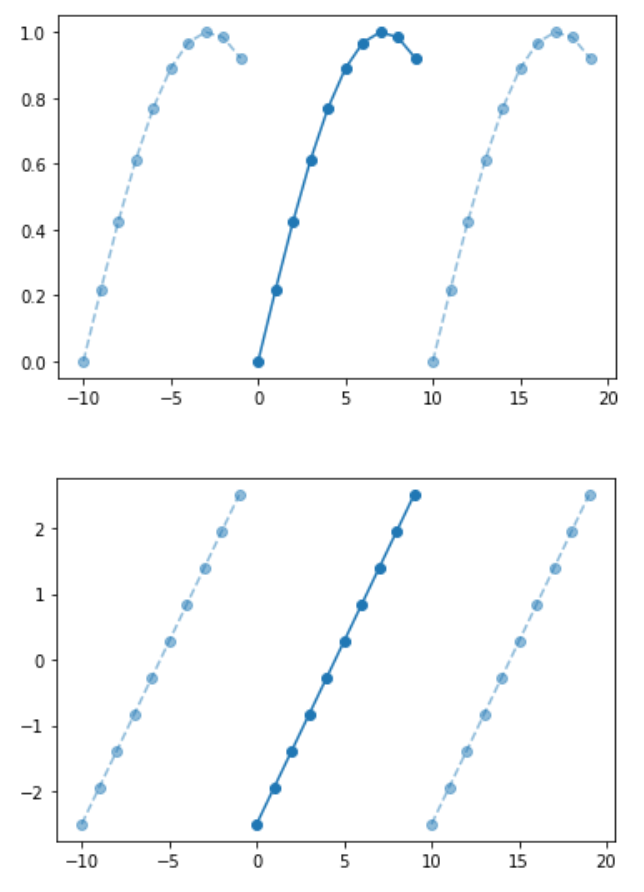
PeriodicArray 的 2 个示例:“基”周期以深蓝色从 0 到 N 绘制,而其他 2 个周期在前后添加,以表示我们正在处理周期序列的事实(由作者制作)。
六、循环卷积,慢速方式
现在让我们实现上面看到的循环卷积方程。使用索引和模运算符,非常简单:
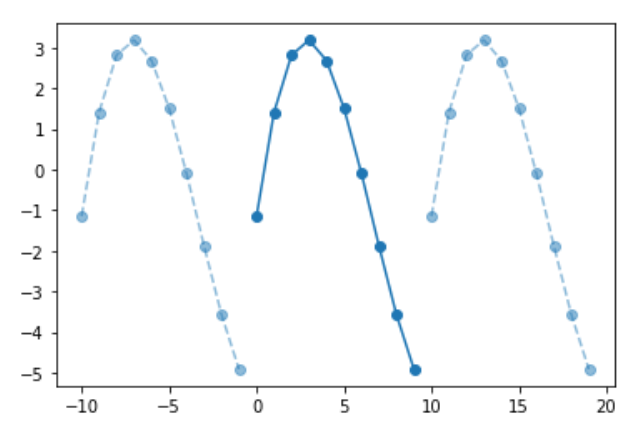
上述2个周期序列之间的循环卷积(由作者制作)。
太好了,我们现在可以看到两个信号之间的循环卷积是什么样子的。将所有内容放在一个数字中:
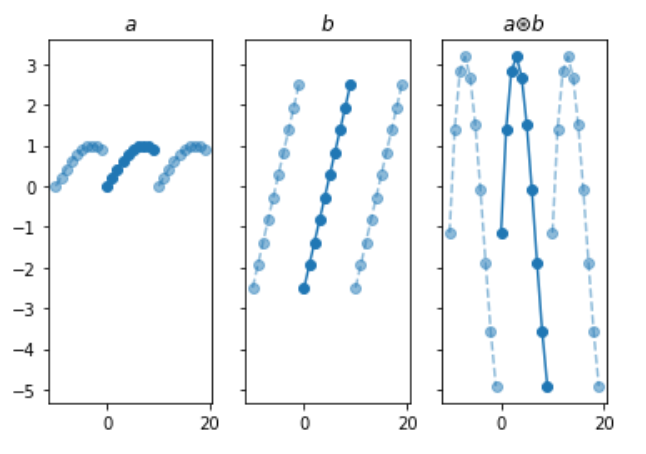
左:第一个周期数组。中间:第二周期数组。右:2个周期数组的循环卷积,这也是一个周期数组(由作者制作)。
现在这个解决方案运行得很好,但它有一个主要缺陷:它很慢。如您所见,我们必须经历 2 个嵌套循环来计算结果:一个用于结果数组中的每个位置,一个用于计算该位置的结果:我们说算法是 O(N²),随着 N 的增加,操作次数将随着 N 的平方而增加。
对于示例中的小型数组,这不是问题,但随着数组的增长,它将成为主要问题。
此外,在python中,对数值数据的循环在大多数情况下被认为是一种不好的做法。一定有更好的方法...
七、循环卷积,傅里叶方式
这就是傅里叶变换和卷积定理发挥作用的地方。由于离散傅里叶变换的实现方式,使用快速傅里叶变换(FFT)以非常快速和优化的方式实现,操作非常快(我们说FFT是O(N log N),这比O(N²)要好得多)。
使用卷积定理,我们可以利用 2 个序列的 DFT 的乘积,当使用逆 DFT 转换回时域时,我们得到输入时间序列的卷积。换句话说,我们有:
![]()
使用直接和逆傅里叶变换的x和y之间的循环卷积(由作者制作)。
其中DFT表示离散傅里叶变换,IDFT表示逆运算。
然后我们可以非常轻松地实现这个算法来计算 x 和 y 的卷积:
def circconv_fast(x, y):"""Fast circular convolution using DFT.Return the full array of the circulard convolution between x and y."""X = np.fft.fft(x)Y = np.fft.fft(y)return np.real(np.fft.ifft(np.multiply(X, Y)))# let's compute the circular convolution for our 2 signals
circ_fast = circconv_fast(periodic_sampled_sinus.base, periodic_slope.base)
circ_fast = PeriodicArray(circ_fast)八、数值和时间比较
最后,让我们验证这两种方法是否产生相同的结果,并比较 python 使用这两种技术计算循环卷积所需的时间:
# compare both ways : "slow" way, and DFT-way
fig, ax = plt.subplots()
ax.plot(circ.base, '-o', label="slow-way")
ax.plot(circ_fast.base, '-o', label="DFT-way")
ax.legend()
ax.set_title('Comparison of 2 ways to compute convolution : \nslow-algebraic way VS using DFT and the convolution theorem')
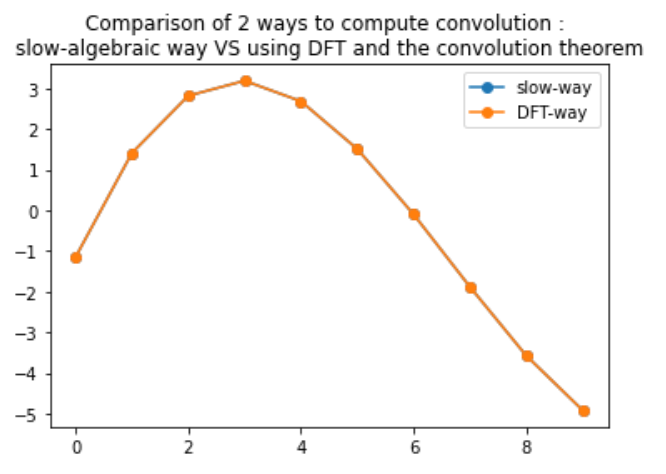
比较两种计算两个周期序列之间循环卷积的方法:“慢速方式”是使用蓝色循环和加法的简单代数,它与橙色的“傅里叶方式”叠加。两种方法给出的结果完全相同(精确到数值精度)(由作者制作)。
这是完美的搭配!两者在数值方面是严格等效的。
现在进行时间比较:
N = 1000
long_x = np.sin(2*np.pi*1*np.linspace(0, np.pi/10, N))
long_y = np.cos(2*np.pi*1*np.linspace(0, np.pi/10, N))print(circconv(long_x, long_y))
print(circconv_fast(long_x, long_y))
# first make sure that both method yield the same result
assert np.allclose(circconv(long_x, long_y), circconv_fast(long_x, long_y))%timeit circconv(long_x, long_y)
%timeit circconv_fast(long_x, long_y)# for N = 10 : 90.2 µs ± 10.2 µs for the slow way VS 14.1 µs ± 161 ns for the DFT-way
# for N = 1000 : 579 ms ± 9.14 ms for the slow way VS 69.4 µs ± 2.35 µs for the DFT-wayfrom physipy import units
ms = units['ms']
mus = units['mus']
print("Gain in speed for 10 samples length: ", 90*mus/(14*mus))
print("Gain in speed for 1000 samples length: ", 579*ms/(69*mus))结果是:
- 对于 N=10 个样本,DFT 快 6 倍
- 对于 N=1000 个样本,DFT 的速度快约 10000 倍
这是巨大的!现在考虑一下,当您分析包含成千上万个样本的时间序列时,它可以为您带来什么!
Fourier Transform for Time Series: Fast Convolution Explained with numpy | by Yoann Mocquin | Jul, 2023 | Towards Data Science
相关文章:

【数据挖掘】时间序列的傅里叶变换:用numpy解释的快速卷积
一、说明 本篇告诉大家一个高级数学模型,即傅里叶模型的使用; 当今,傅里叶变换及其所有变体构成了我们现代世界的基础,为压缩、通信、图像处理等技术提供了动力。我们从根源上理解,从根本上应用,这是值得付…...
Chatgpt Web API 创建对话,免费,不计token数量,模仿网页提交对话
Chatgpt API 是收费的,按token使用量计费 Chatgpt Web API 免费的,只要有账号就可以使用。 curl https://chat.openai.com/backend-api/conversation \-H authority: chat.openai.com \-H accept: text/event-stream \-H accept-language: zh-CN,zh;q…...
嵌入式软件—RK3568开发环境搭建
一、RK3568 1.1 开发板特点 BSP比较大,对于电脑内存和存储空间要求高 1.2 BSP BSP(Board Support Package,板级支持包),类似于PC系统中BIOS和驱动程序的集合,BSP包含的范围更广,除了外设驱动…...

使用 OpenCV 和 GrabCut 算法进行交互式背景去除
一、说明 我想,任何人都可以尝试从图像中删除背景。当然,有大量可用的软件或工具能够做到这一点,但其中一些可能很昂贵。但是,我知道有人使用窗口绘画3D魔术选择或PowerPoint背景去除来删除背景。 如果您是计算机视觉领域的初学者…...

在Windows server 2012上使用virtualBox运行CentOS7虚拟机,被强制休眠(二)
问题场景 本月7月10日处理了一个虚拟机被强制暂停的问题,详见:在Windows server 2012上使用virtualBox运行CentOS7虚拟机,被强制暂停当时是由于C盘存储空间不足,导致虚拟机被强制暂停,将虚拟机迁移后,问题…...
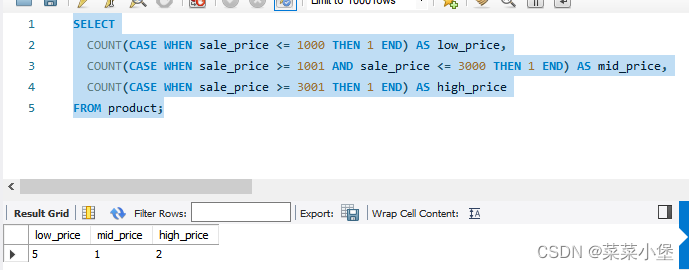
sql学习笔记
sql语句优先级 FROM → WHERE → GROUP BY → SELECT → HAVING → ORDER BY sql case用法 例题: 按照销售单价( sale_price )对练习 3.6 中的 product(商品)表中的商品进行如下分类。 低档商品:销售单价在1000日元以下&#x…...

Ubuntu 20.04.4 LTS安装Terminator终端(Linux系统推荐)
Terminator终端可以在一个窗口中创建多个终端,并且可以水平、垂直分割,运行ROS时很方便。 sudo apt install terminator这样安装完成后,使用快捷键Ctrl Alt T打开的就是新安装的terminator终端,可以使用以下方法仍然打开ubuntu默…...

22. 括号生成
题目描述 数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:["((()))","(()())","(())()","()(())",&…...

WPF实战学习笔记05-首页界面
首页界面 新建文件 添加文件[类型:用户控件] ./Common/Models/TaskBars.cs ./Common/Models/ToDoDto.cs ./Common/Models/MemoDto.cs 新建类 TaskBars.cs using System; using System.Collections.Generic; using System.Linq; using Sy…...
一文带你迅速入门SprIngMVC,看这一篇就足够了!
0. 什么是SpringMVC 要知道什么是SpringMVC,我们首先得知道什么 MVC,MVC是软件工程中的一种架构模式,分为 Model、View、Control。它把软件系统分为模型、视图和控制器三个基本部分。 Model:模型,应用程序负责数据逻…...

js路由跳转时放弃正在pending的请求
在单页面应用中通常会对请求进行catch处理,如果用户打开a页面后页面发出了一个请求去获取aaa,但是由于某种原因请求一直在pending。此时用户又进入了b页面,在浏览时a页面的请求失败了,然后页面弹出提示:“数据aaa请求失…...
-0723)
LeetCode(sql)-0723
聚合函数 620 select * from cinema where mod(id,2)1 and description <> boring order by rating desc1251 select p.product_id, Round(sum(price*units)/sum(units),2)as average_price from UnitsSold u left join Prices p using(product_id) where purchase_d…...

【C++】开源:grpc远程过程调用(RPC)配置与使用
😏★,:.☆( ̄▽ ̄)/$:.★ 😏 这篇文章主要介绍grpc远程过程调用(RPC)配置与使用。 无专精则不能成,无涉猎则不能通。。——梁启超 欢迎来到我的博客,一起学习,共同进步。 喜…...
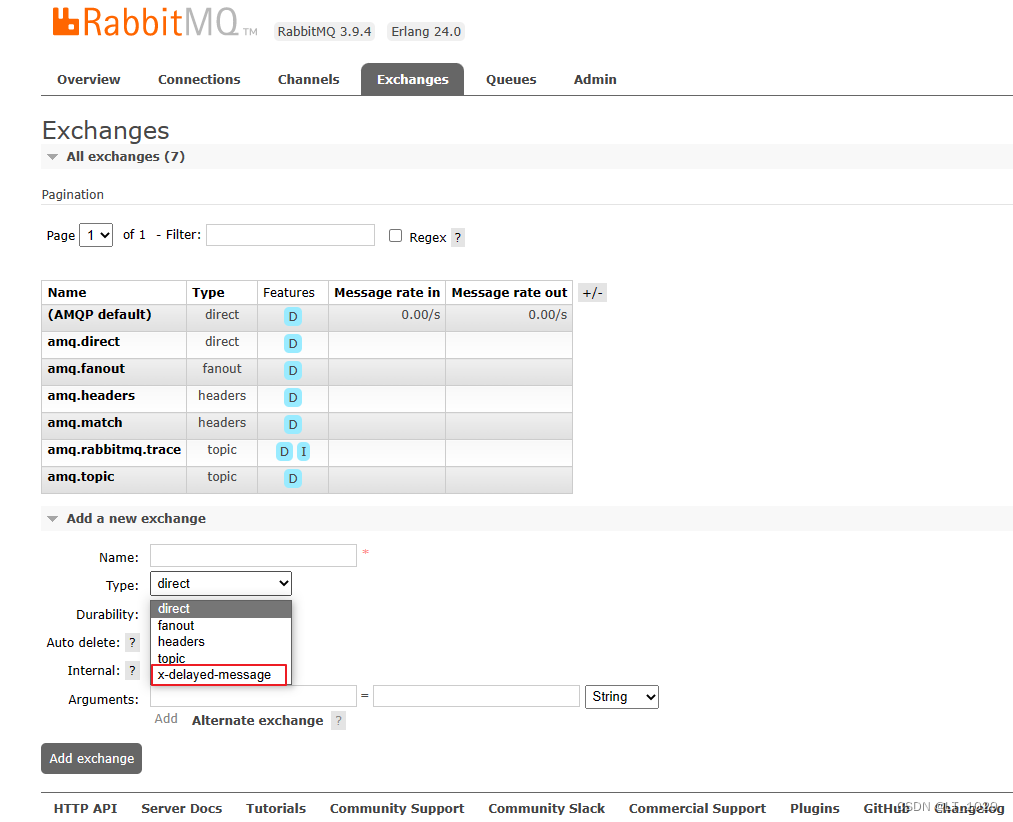
rabbitmq模块启动报java.net.SocketException: socket closed的解决方法
问题 最近在接手一个项目时,使用的是spring-cloud微服务构架,mq消息消费模块是单独一个模块,但启动这个模块一直报如下错误: java.net.SocketException: socket closed 这个错误是这个模块注册不到nacos报的错,刚开…...

uni-app 中定时器的使用
学习目标: 学习目标如下所示: uniapp中通过使用uni-app提供的定时器API来实现定时器功能。 学习内容: 内容如下所示: **uni-app的定时器API分为两种: 1.第一种方式: setTimeout函数,用于设置一…...

基于物联网、视频监控与AI视觉技术的智慧电厂项目智能化改造方案
一、项目背景 现阶段,电力行业很多企业都在部署摄像头对电力巡检现场状况进行远程监控,但是存在人工查看费时、疲劳、出现问题无法第一时间发现等管理弊端,而且安全事件主要依靠人工经验判断分析、管控,效率十分低下。 为解决上述…...
内网穿透远程查看内网监控摄像头
内网穿透远程查看内网监控摄像头 在现代社会中,大家总是奔波于家和公司之间。大部分时间用于工作中,也就很难及时知晓家中的动态情况,对于家中有老人、小孩或宠物的(甚至对居住环境安全不放心的),这已然是…...
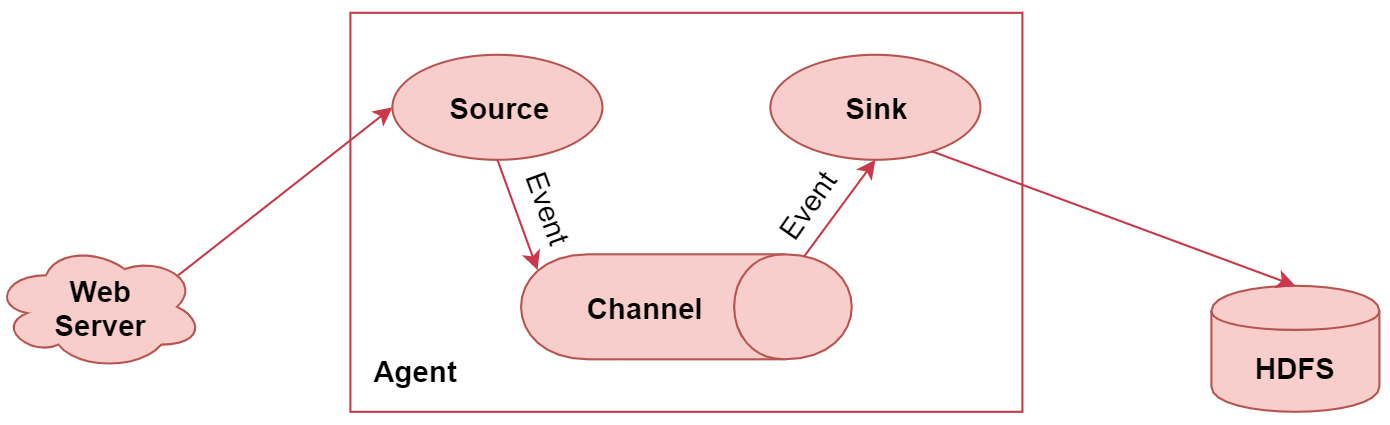
【Flume 01】Flume简介、部署、组件
1 Flume简介 Flume是一个高可用、高可靠、分布式的海量日志采集、聚合和传输的系统 主要特性: 它有一个简单、灵活的基于流的数据流结构(使用Event封装)具有负载均衡机制和故障转移机制一个简单可扩展的数据模型(Source、Channel、Sink) Sou…...
三款即时通讯工具推荐:J2L3x、Telegram、WhatsApp 你选哪个?
1、J2L3x J2L3x 是一款受欢迎的即时通讯工具,广泛应用于企业团队之间的沟通和协作。它提供了多种通讯方式,包括群组聊天、私人消息和文件共享等,还可以方便地与其他应用程序和服务集成。即使你不在工作场所,你也可以在任何地方使…...

C++ 单例模式(介绍+实现)
文章目录 一. 设计模式二. 单例模式三. 饿汉模式四. 懒汉模式结束语 一. 设计模式 单例模式是一种设计模式 设计模式(Design Pattern)是一套被反复使用,多数人知晓的,经过分类的,代码设计经验的总结。 为什么要有设计模式 就像人类历史发展会…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
